Editors Note: In future research we wish to invite readers to also consider the implications for preservice education in the use of technology in mathematics education. It is critical for our readers to investigate the implementation gap addressed by this author, as well as the development of the three forms of technological knowledge: technological knowledge, pedagogical knowledge of technology, and pedagogical content knowledge of technology.
Ginny Keen and Iris Johnson
Mathematics Education Editors
Over the past 25 years, research and instruction in mathematics education have witnessed a gradual shift to a constructivist, inquiry-based view of teaching and learning. Advances in mathematics education technology have supported the shift from teacher-centered instruction to student-centered instruction, in which the teacher serves as a facilitator for learning. Preservice and in-service training often offer skill-based technology sessions focusing on how specific technological tools work, but lack a sense of vision regarding issues of appropriate pedagogy and curriculum integration (Hughes, 2004). Despite exposure to a variety of personal technologies Keating and Evans (2001) found that preservice teachers expressed doubts as to their ability to incorporate technology effectively in the classroom.
Regarding the teaching and learning of geometry using technology, Niess (2006) commented that many high school geometry teachers graduated long before much of the current technology was available, while others may have attended an undergraduate or graduate program that did not include the use of technology. In either case, practicing teachers need to know how to learn and teach with technology in order to integrate appropriate technologies effectively into their teaching practice.
The mathematics education community is currently faced with the challenge of creating focused professional development opportunities or programs that should be
dedicated to helping the teachers become knowledgeable about the technology while being challenged to integrate technologies in their teaching. These programs need to recognize and emanate from the teachers’ experiences and provide them with experiences in teaching mathematics with technology. (Niess, 2006, p. 4)
At the high school level, the use of a dynamic geometry environment is an ideal setting for the examination of a constructivist technology tool. Using an emergent perspective this paper will describe integration of such technology in the high school geometry curriculum. A teacher development experiment (Simon, 2000) was conducted with the goal of exploring the pedagogical, technological, and mathematical development of a master teacher. This methodological approach also could be classified as “learning technology by design” (Mishra & Koehler, 2006), since the technology was learned by the classroom teacher through the cyclic act of designing or retooling the geometry course.
Related Literature
The National Council of Teachers of Mathematics (NCTM) outlined the roles and benefits of using technology in mathematics education in Principles and Standards for School Mathematics (PSSM; NCTM, 2000). The Technology Principle, included in the PSSM stated, “Electronic technologies—computers and calculators—are essential tools for teaching, learning, and doing mathematics. They furnish visual images of mathematical ideas, they facilitate organizing and analyzing data, and they communicate efficiently and accurately” (p. 24). In addition, the PSSM specifically referenced the benefits of a dynamic geometry environment for student learning of geometric concepts. Within this type of program, a student can drag a node (vertex) around while the geometric shape on the screen changes, giving the student immediate feedback regarding potentially invariant properties and specific measurements (provided the figure was constructed correctly). Technology also provides a focal point as students discuss with one another, and with their teacher, the objects on the screen and the effects of the various dynamic transformations that the technology allows.
Although technology use does not guarantee a change in the teacher’s geometry instruction, Chazan and Yerushalmy (1998) maintained that it best supports the type of student thinking called for by the NCTM. Ideally, insight gained from the use of a dynamic geometry system such as Cabri (1996) or The Geometer’s Sketchpad (Jackiw, 2001; see also http://www.dynamicgeometry.com/general_resources/ bibliography.php – Anchor-Sketchpad-35882) potentially aids the teacher in assessment and future instructional planning with respect to the geometry curriculum.
The high school geometry curriculum is defined, for the purpose of this paper, as the study of geometric figures with both a pure and applied approach. The main themes are similarity and congruence, which provide exploration of two- and three-dimensional shapes, as well as a context for the study of proof. Proof is approached from the standpoint of a logical argument. In a discussion of the proof process, de Villiers (1998) cited the role of conviction and how it drives mathematicians to develop proof. He went on to say that, logically, mathematicians require a formal proof, but psychologically, they are led to it from experimental exploration or intuition.
Student intuition can be developed through exploration in a dynamic geometry environment provided by software such as Cabri or The Geometer’s Sketchpad (GSP). Chazan (1993) highlighted the role of evidence in convincing students of the validity of a deductively proven theorem. He found that students viewed a deductive proof as a single case and seldom appreciated the generic aspect of it. Although some educators may feel that the role of proof may be diminished in the high school curriculum, research thus far suggests that the discussion of why a conjecture is true leads to a more secure role of proof (and counterexample) in the high school curriculum (Chazan & Yerushalmy, 1998; de Villiers, 1998).
An initial literature review located a few studies on student learning with GSP or Cabri (Choi-koh, 1999; July, 2001; Laborde, 2000; Lester, 1996; Mariotti, 2000), but only one study with a specific focus on the teachers’ needs as they began teaching with GSP (as described in McDougall, 1996, 1997). McDougall (1997) investigated teachers’ initial experiences with GSP integration through case studies of four middle school teachers. These teachers experienced a loss of control in three areas that McDougall classified as “control-as-management of the learning environment, control-as-personal, and control-as-professional” issues (p. 7).
Management control issues surfaced as the teachers “believed the new environment impaired their ability to maintain discipline” (McDougall, 1997, abstract). Personal control issues were related to moments of vulnerability that surface with the introduction of new technology and changes in expectations for the classroom teacher with regard to holding a position of authority, leadership, and expertise in the classroom. Professional control issues highlighted considerations for a change in the teacher’s role as the answer source or director of learning experiences, to the teacher as the facilitator of learning, open-ended explorations, and student discovery (McDougall, 1997).
McDougall’s findings suggest several key provisions necessary to sustain classroom teachers involved in the initial implementation of GSP (or other technology). Two provisions consistent with those of Saye (1998) are (a) support from a technology specialist or colleague who can serve as a mentor with technological experience and (b) sufficient release time to experiment with the technology to plan for instruction. McDougall (1997) also suggested that teachers in the initial implementation of GSP should be “valued by school administrators and peers; … engage in reflective activity; … [be] willing to change; … [and] willing to share control of the learning environment with students” (p. 92). General factors that foster technology acceptance and effective use by teachers also include adequate information, leadership, and a sense of obligation for its use (NCTM, 2000).
Method
This study set out to examine and explore the integration of the GSP into the teaching practice of a master teacher through an apprenticeship model within a teacher development experiment. The study provided the master teacher with a mentor (the researcher and author of this paper) to aid with the integration of GSP activities into the teacher’s geometry curriculum. The researcher, at the same time, investigated how the teacher accepted and integrated the program into his instruction. Reflection and analysis of the results confirmed the merit of the general factors identified by McDougall and pointed to the existence of new forms of teacher knowledge necessary to teach effectively with technology.
Teacher Development Experiment
Classroom teaching experiments in a design experiment methodology have emerged to serve the purposes of engineering certain forms of learning and, at the same time, systematically studying the learning taking place with the goal of generating theory (Cobb, Confrey, diSessa, Lehrer, & Schauble, 2003). The literature includes two main sources of information regarding design-based research methodology: a themed issued of Educational Researcher (Kelly, 2003) and Kelly and Lesh (2000).
A teacher development experiment was undertaken in this study because it was suitable to the dual goals of fostering the development of a teacher’s knowledge of teaching with technology through the creation of an intervention and documenting this development as the intervention took place. The research was situated in the classroom where I was able to create the situation and “study development by fostering development as part of a continuous cycle of analysis and intervention” (as recommended by Simon, 2000, p. 336). This study focused on an intervention with one teacher and collected data at the levels of researcher/teacher and teacher/student.
Cobb et al. (2003) referred to the highly interventionist nature of the methodology as a feature of design research and stated, “The intent is to investigate the possibilities for educational improvement by bringing about new forms of learning in order to study them” (p. 10). As is characteristic of design experiments, the design of the intervention was based on an initial conjecture (Cobb et al., 2003). I conjectured that the classroom teacher would, through a mentoring process and an apprenticeship model, first realize the value of using GSP in his geometry instruction and then make the necessary changes in his instruction to teach with GSP. Results of the design experiment thus potentially focused on changes in this particular teacher’s practice, characteristics this teacher possessed that may have contributed to successful technology implementation, and the development of a general theory on the types of teacher knowledge necessary to teach successfully with technology.
Setting and Participants
In the fall term of the 2002-2003 school year, a research study was conducted to explore the feasibility and results that might be obtained from a mentoring relationship between a local high school geometry teacher and the author/researcher, with a focus on the implementation of GSP activities. Following a presentation made to the entire mathematics department in a local high school in May 2002, a teacher named Jacob agreed to participate. I had not met the mathematics faculty prior to the presentation.
The high school was located in a medium-sized Midwestern town and, at the time of the study, the school contained a relatively large Hispanic population (10%). The high school operated on a two-semester block-8 schedule, with students attending four classes on alternating days and all classes on Friday. Jacob had taught at the school since 1968, had completed a master’s degree from the University of Notre Dame, and admitted to having had little experience with GSP but was interested in participating in the study. The mathematics department used a fairly traditional textbook series and had purchased an updated GSP program (version 4) that no one was using.
As a participant in the study, I took on the dual role of mentor to Jacob, promoting a split between the roles of observer and active participant. I began my involvement with the use of GSP in my own public high school teaching from 1993 to 1996. During this time I preferred to have students develop “sketches” and created a social norm for class work. Working in pairs on one computer, students followed a set of written directions on a worksheet to guide them in the use of GSP to construct a given figure. Students were typically asked to measure some aspect of the figure—either segments or angles—manipulate the figure, and then make a conjecture (e.g., “the sum of the measures of the remote interior angles of a triangle equals the measure of the exterior angle”). In some cases the sketch (file) would be printed and turned in, but when an animation was required, the sketch would be submitted electronically. My role was to facilitate the activity by asking questions, answering questions regarding how the program worked, and helping to resolve obvious, yet sometimes mysterious errors. The role of the technology was to aid students in the development of an empirical understanding of geometric theorems.
When I moved to the university setting, I taught the modern geometry course in a similar fashion, but with additional expectations for college students. I expected more rigorous content, including non-Euclidean geometry, and I expected students to create a presentation using the GSP copy-page feature to share their development of the stages of a particular proof. This experience with the use of GSP put me in a favorable position to act as the mentor for the study.
Study Description and Discussion
Data for this study were collected through researcher field notes (journal), email communications, an exit interview, member checking, and classroom observations. Jacob agreed to read and comment on a draft of this paper and validated the accuracy of what is reported here (personal communication, August 23, 2007). I taught GSP activities almost every Tuesday, from September to November 2002, to Jacob’s students who were scheduled for Tuesday classes. Every Tuesday and Wednesday Jacob’s geometry classes were scheduled into the computer lab for the first half of the 90-minute class. On Tuesdays I modeled instruction in one regular and two honors geometry classes. The following day, Jacob repeated the GSP activities with the remaining geometry sections while I was not present due to conflicts with my own teaching schedule.
One early issue was using GSP with the regular students. Jacob sent the following email:
I am having serious misgivings regarding the regular sections … primarily because it has been Many [sic] years since I have taught a non-honors geometry and have little or no feel for how tough it will be to get all the curriculum in. I AM willing to give it a try with the understanding that our lab time may be much more restricted in that class. (May 30, 2002)
Jacob was now teaching two regular geometry sections because he requested a schedule of five geometry classes, giving up precalculus, in order to dedicate his entire schedule to the integration of GSP.
The study officially began at the start of the 2002-2003 school year. During the first 2 weeks Jacob and I communicated about technological issues and content goals, but the use of GSP was delayed in the computer lab due to state testing scheduled in the computer lab. As the work in the classroom began, Jacob and I engaged in discussion and tasks focused on the selection of content topics for instruction, my modeling of instruction, and concerns related to the sequencing of the content.
Topics Selection and Instructional Modeling
During the beginning work of the study, Jacob typically emailed a list of topics from which I was to choose. Then, I selected a lab (handout) from a published source, created a lab, or outlined a demonstration (no handout) to be done with the students. In a typical session I completed a demonstration and a lab activity. Lab activities completed in the study focused on introducing vocabulary and triangle theorems (see Table 1).
Table 1
Name and Date of Geometer’s Sketchpad Activity
| Date | Week | Lab Topic or Name |
| Sept 17 | 3 | Copy a segment; introducing angles |
| Sept 24 | 4 | Midpoint formula; slopes of parallel and perpendicular lines |
| Oct 1 | 5 | GSP Tours 1 and 2 (parallelogram in a quadrilateral construction) |
| Oct 8 | 6 | Perspective drawings; rotation of a point demo; rotation lab #1 (mentor created) |
| Oct 15 | 7 | Perpendicular bisector theorem; rotation lab #2 (mentor created), introduction to translations |
| Oct 22 | 8 | Burning Tent problem (on reflections); vertical angle theorem |
| Nov 5 | 10 | Triangle (angle) theorems |
| Nov 12 | 11 | Triangle congruence theorems |
| Nov 19 | 12 | Triangles: medians and perpendicular bisectors |
While I conducted lessons in the lab, Jacob assumed a number of roles. In the first two lab sessions Jacob worked through the lab activities on a computer, observed the instruction, and observed students. By the third week Jacob began to work with students. He easily adapted to the role of facilitator and asked questions like, “How do you know that?” and “Why did that do that?” or “What is the relationship here?” As the semester progressed he began assuming a more decisive role in selecting and then designing the activities to be completed in the lab. The following email communications illustrate the progress made in this area:
Looking ahead: 1) equations of parallel and perpendicular lines 2) perspective drawings 3) rotations 4) also, midpoint formula will be among the things we will do, hopefully by mid-October, so would be fine to intro in the lab next week … your choice. (September 19)
I would like to do the lab on page 28. Then we can do at least the 1st of your rotation labs. … I like them. BEFORE doing the rotation lab, it would be good to simply have them rotate a segment AB around the center O, measure AO, A’O, BO, B’O, angle AOA’ and BOB’ so they understand what a rotation does. (October 8)
Planning to do the orthocenter and incenter constructions for triangles. Page 77 first and do it through Explore more #1, then page 75, 76 but not the Explore more. I am comfortable doing these if you want to observe OR even more comfortable observing you … your choice. … I thought we would do the Euler line next. (November 27)
The emails depict the progression in Jacob’s ownership of the curricular content of the labs. However, assuming the duties of lead teacher on Tuesdays took much longer than I expected (see the November 27 email). While Jacob would teach the labs each Wednesday, he took advantage of the opportunity to observe my facilitation of the lessons provided on Tuesdays. Jacob was able to watch and reflect in real time, which is difficult to do while actually teaching. Jacob felt it helped him skip some of the learning curve normally experienced while experimenting with a new instructional tool. It should be noted that once a lab was introduced, Jacob and I worked as a team, helping the students in the lab. Comments from the exit interview addressed this issue:
The thing that happened here was by having you in the classroom with me, that was just a tremendous experience for me, and [sic] easy way for me to learn GSP, which I was not terribly familiar with, I had minimum exposure to it, but for me to learn that and also, obviously, for me to see how you interacted and expected the students to use sketchpad …. The format was that the initial session, the initial class session, on any particular lab, that you conducted that and I observed and then I went ahead and did the others on my own. Yeah, that was just a wonderful process because modeling how to work with the students as well as learning the actual function of Sketchpad was a very, very comfortable, and efficient way to learn it.
Content Sequencing Concern
The act of teaching requires advanced planning in order to meet course objectives. The commitment of having a fixed lab day each week was an initial source of concern for Jacob. He felt there needed to be a tight sequencing of topics between the days in and out of the lab. Since the study design restricted lab use to a specific day each week, topics that had not been introduced yet had to be selected. This restriction turned out to have a positive result on the students’ learning of these chosen topics. Jacob noted in October that since his students had been initially exposed to a topic in the lab, they knew it better. Jacob commented that in classroom discussions he often found that his students recalled a lab they had completed:
Jacob stated he wasn’t sure at the beginning of the year how the GSP work would mesh with his curriculum but that it is working out well and that he needs to spend more time working on the integration of ideas between the lab and the book. For example, we had started rotations and he has not gotten to that yet – (next week) but he stated they would probably know it better because of the labs that we are doing. (Field notes, October 8)
Jacob reflected on the sequencing issue in the exit interview:
Well, one of my concerns, I guess, before we started, was the need to tightly sequence the things we were introducing with what we were doing in the classroom and I found out as we went that that really didn’t need to be an issue or concern at all.
Results
Jacob experienced two main changes in his teaching practice as a result of implementing GSP through the apprenticeship model: an enhancement of the goals of the geometry course to include communication and a shift to inquiry-based instruction.
Communication Goal
Jacob was aware of a schoolwide goal of increasing students’ ability to communicate. Through the use of GSP activities he found a natural way to foster communication in the mathematics classroom, as students responded to specific lab questions by typing their explanations or conjectures into their GSP sketches. When reflecting on the use of GSP, Jacob stated that the use of the program helped him fulfill not only geometry goals but also helped him develop the students’ communication skills.
One emphasis at our school right now is to work with students on the communication process, in all classes, not just their language arts classes and Sketchpad is one way to do this. Often the labs are printed out and the students have to read and follow the directions. Then, often times, we have them write responses to those so we are doing much more communicating. (Exit interview)
An example of Jacob working with the students on communication was noted in a particular lab session in which he used a class handout and overhead sheet to share a variety of student responses on geometric rotations. Figure 1 includes four of the five student responses displayed in the lab; the fifth, almost identical to one of the four, is omitted here. In the class session the students read through the different student responses and engaged in a discussion regarding what had been written. More importantly, the students discussed how to word their responses in the future so that they would be correct, understandable, and concise. Work with GSP, thus, was used to promote both verbal and written communication in the classroom.
| HOW TO FIND THE CENTER OF A ROTATION: When given a segment and its rotation, connect point A to A’ and B to B’. Then create the perpendicular bisectors of the segments just created. Where the bisectors intersect is the center. | |
| Connect the points and their images. Construct a perpendicular bisector of each new segment. Construct the intersection of the perpendiculars. This is the center of rotation. | The center is where the perpendicular bisectors of B,B’ and A, A’ intersect. |
| To find the center of a segment and its image that has been reflected* 90 degrees you must connect each point with its image or prime with a segment. Then put its mid-point on those segments you just made. Then make the perpendicular bisectors using those end points. With those two perpendicular bisectors find the intersection. The angle with the points: a point, the intersection, and the point’s prime should be the same as the original rotation you made. That intersection is the center. *This word was circled on the overhead sheet and minor spelling errors were corrected. | |
Figure 1. Student explanations for constructing the center of rotation.
Inquiry-Based Instruction
Jacob reported that he had definitely made changes in instructional delivery due to observing students in the lab as they engaged with the GSP activities. He noted that the exploratory nature of the GSP environment helped him move away from a lecture format of instruction to a guided-discovery, or inquiry-based approach, in which students were challenged to formulate, test, and confirm conjectures. The exit interview provided the following summary:
I think in terms of getting the students, having them take a hands-on approach towards discovery had led me to see how much better it is when kids are actively involved with the initial step in learning. So, yes, for me at least, there had been less of a presentation of “here it is” presented by me and trying to get them active, even in the business of class discussion, to get them more involved in the actual discovery or learning process. I know that has taken place [italics added].
Jacob pointed out the power of GSP in looking at multiple cases of a situation:
All of these things we had done in past years, but we didn’t do it with GSP. We had to construct our own figures. GSP enables us to do so much. It is just so much more efficient, students, rather than looking at just one example that they have created [paper and pencil], they can create as many examples as they want and make comparisons.
These transcript data indicate a transition in Jacob’s instruction from direct teaching to a discovery approach. Jacob also shared that engaging students with the geometry content through GSP had a powerful impact on student motivation. In a lab on polygons, conducted 3 months after the conclusion of the pilot study, Jacob stated, “Students would scream with delight when they got it, when they finally saw the relationship between the two [measurements]” (Email, February 25, 2003).
Senger (1999) traced the change process from a beginning level of an awareness of something new through the experimental change in teaching practice and verbalization to the final stage of being convinced. In November, I witnessed a sign that Jacob was convinced of his new belief. On November 5, two math teachers (at different times, while in the hall) both spoke highly of the geometry study. One asked if he could get copies of the labs that had been done in the computer lab, and the other asked about the duration of the study at their school and possible participation of additional teachers. Since these two teachers were not involved with the study, their interest had to have come from conversations with Jacob. While engaged in conversations regarding the use of GSP Jacob had persuaded his peers of its merits. This type of verbalization is characteristic of Senger’s final stage of change: being convinced. To engage in persuasive conversation is an indication that a person has begun to integrate the new knowledge into their existing belief system (Senger, 1999).
Another source of evidence that Jacob’s teaching practice had truly changed is noted in an observation of his activity following the conclusion of my time in the school. Although the study formally ended in November 2002, Jacob continued to take his classes to the lab at the same pace as in the fall semester.
Labs we have done since we spoke last: Measuring arcs in circles, central angles, inscribed angles. Also, tangent to a circle, lengths of tangent segments to a circle (I added angle formed by tan segments and a TOUGH bonus for constructing a tangent to a circle from an exterior point). Labs are unavailable most of April and May due to MAPS testing L. (Email, April 3, 2003)
This communication illustrates a complete inclusion of GSP activities into Jacob’s teaching. The statement that he was not able to use the computer lab at the end of the year was accompanied by an unhappy face icon.
Discussion
The Apprenticeship Model
I used an apprenticeship model to describe the actions and interactions of the classroom teacher and myself during the pilot study. The design and results of the study are discussed through the lens of the apprenticeship model. From the outset of the study Jacob had declined an invitation to be the focus of the investigation, which restricted data gathering to conversations captured in my field notes and electronic communications I saved and printed.
However, at the conclusion of the study Jacob felt more comfortable with the research and retroactively agreed to become the main focus, which quickly prompted an exit interview. This interview took place after school in December in Jacob’s classroom and was subsequently transcribed. The lack of additional data that could have been gathered placed a limitation on the discussion since the results were not able to be triangulated through multiple data sources (additional audio or video tapes).
Obtaining training about how a particular technology works in an in-service meeting, a preservice course, or by self-study in reading a manual does not necessarily guarantee successful implementation of that technology in alignment with goals of NCTM’s (2000) Technology Principle. Considering this implementation gap I designed a teacher development experiment based on an apprenticeship structure, with the goal of transmitting teacher knowledge of how to use the technology and also how to provide instruction to support the learning of mathematics with the use of the technology by simply modeling instruction within a teacher’s classroom and discussing what was taking place.
From prior experience teaching high school geometry I felt that modeling was the best way to show that GSP can be successful for teaching students to think and reason. After completing the main study of my doctoral dissertation, I discovered that this model also did not guarantee success. In the final analysis I admitted that the experience of the pilot study was comparable to a rookie getting a home run the first time at bat in the major leagues. Factors supporting success are discussed later in the section highlighting implications for further research. I documented factors seeming to inhibit successful integration of GSP, after working with two teachers at a different location in fall 2003 (Shafer, 2004).
The apprenticeship model created to describe the pilot study followed a cyclic trajectory (Figure 2). In the first stage of the cycle Jacob (referred to as Teacher in the figure) presented me with a list of possible topics and I (referred to as Mentor in the figure) selected an appropriate lab. Over time Jacob assumed the role of task selection (Week 6). In the second stage of the model, instruction took place. The figure indicates that instruction transferred from me to Jacob at Week 11. The third stage involved assessment and reflection. Over time it became clear that the classroom integration of GSP labs arose in this third stage.
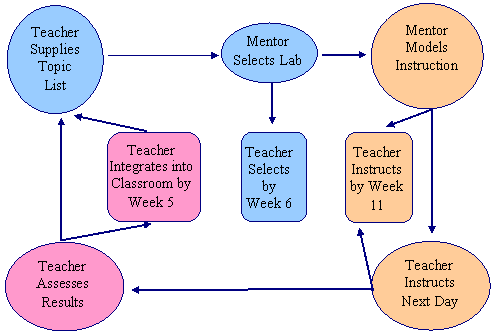 Figure 2. Apprenticeship model.
Figure 2. Apprenticeship model.
Forms of Technological Knowledge
As I began the process of integrating results from the pilot study and my main doctoral study (Shafer, 2004), I became aware of three forms of technological knowledge necessary to teach with GSP: technological knowledge, pedagogical knowledge of technology, and pedagogical content knowledge of technology. Technological knowledge (TK) compares with Shulman’s (1987) content knowledge construct. “Teachers need to possess an in-depth knowledge of how the given technology works” such that knowledge of the technology is equivalent to knowledge of the mathematical content (Shafer, 2004, p. 174).
Since technologies are continually evolving and changing, this technological knowledge may appear to be a tenuous construct. An example in this context includes knowing the various menu options within GSP. Teachers need to be fluent with the features of the Construct, Transform, Measure, Display and Edit menus in GSP.
Pedagogical knowledge of technology (now commonly referred to as Technological Pedagogical Knowledge or TPK) is closely related to Shulman’s (1987) pedagogical knowledge construct, which is defined as the teachers’ knowledge of teaching procedures such as effective strategies for planning, classroom routines, behavior management techniques, classroom organizational procedures, and motivational techniques. This form of knowledge was illustrated in this study by suggested teachers’ actions I modeled with Jacob’s students.
Pedagogical content knowledge of technology is now commonly referred to as technological pedagogical content knowledge or TPCK. Pedagogical content knowledge was defined by Shulman (1987) as the knowledge of how students think and learn with specific attention to how this knowledge occurs within specific mathematical content areas. I defined pedagogical content knowledge of technology as the teachers’ knowledge of how “students think about and learn mathematics with technology” (Shafer, 2004, p. 175).
Evidence supporting the development of these three constructs has recently appeared in print with information generating from a variety of content areas (Hughes, 2005; Margerum-Leys & Marx, 2002; Pierson, 2001). The most comprehensive discussion of a TPCK framework for teacher knowledge culminated from Mishra and Koehler’s (2006) work with design teams. Niess (2005) also described the development of the term Technology Pedagogical Content Knowledge or “technology enhanced PCK” in her work with preservice science and mathematics teachers. In each case the researchers extended Shulman’s constructs of content and pedagogy to include an additional construct of technology and the various intersections formed. For more information on TPCK see Mishra and Koehler’s wiki: http://www.tpck.org/tpck/index.php?title=Main_Page
Technological pedagogical knowledge. Many of the labs in this study were taken from Exploring Geometry With The Geometer’s Sketchpad (Bennett, 1999), and I developed a few. As I facilitated instruction in the computer lab, classroom procedures were established. In most cases the students were given a worksheet that had written directions as well as a sample diagram. Students were usually required to turn in a printout of their file that contained the required sketch and accompanying information in a text box. Pacing of the class time can be an issue, since the work must be completed and printed on machines while in the lab. Since some students finish quicker than others, I had an extension problem for them to complete or, in some cases, these students assisted classmates who were struggling. Other specific TPK procedures highlighted in this study involved grouping of students, creating an equitable participatory learning environment, monitoring student understanding of instruction, providing efficient printouts of student work, and facilitating instruction.
Pairing students to work on the computers—even though there were enough computers for each student in some classes—promoted student discourse. In some cases students needed to be strongly encouraged to talk to their partners. One routine that was taught was to trade the mouse. When working with a partner the student controlling the mouse took a more active role with the technology while the one watching assumed a passive role. In order to create equity in the learning experience I would say “Okay, it is time to trade the mouse,” and I would actually monitor that this trade occurred.
Another TPK routine established was displaying a student’s work on the teacher’s computer during the lab session. A projection unit had to be brought into the lab during our lab sessions and attached to a computer close to the front of the lab. In any given class a student might be asked to assist by operating the computer connected to the projection unit. What is now more typical in computer labs is a projection unit attached to a computer (i.e., teacher computer) facing the student computers. This organization creates a problem when the teacher cannot see what is displayed on student machines.
Putting a student on the teacher computer has the advantage of releasing the teacher from standing in one spot to operate the technology as directions are given, typically out of site of the student monitors. By making this simple change the teacher can better focus on the instruction and students’ active interpretation and understanding of the instructions. In fact, if the student on the teacher computer made errors that everyone was able to see, the potential for a wonderful teaching moment naturally arose.
As students prepared to submit their completed work, a routine for printing a GSP file became necessary. In many instances the sketches students had created would spill over horizontally across two pages instead of one. Students would waste paper through their repeated attempts to reposition figures on the page. Students were taught to use the Print Preview feature effectively, send their file to the printer, and leave the page in the tray for me to collect (which also reduced student movement in the lab).
One final area of TPK was the facilitation of instruction. Teaching geometry with the goal of exploration and discovery required me to assume a pedagogical approach that scaffolded instruction guided by a strong sense of knowing how much and when to provide support. Knowing which prompts to give to students required knowledge at the TPCK intersection.
In the second stage of the apprenticeship model I modeled TPK by teaching the Tuesday geometry classes to provide a guide for the geometry classes taught by Jacob the following day. Although this process was the norm, the order was switched in Week 10 when Jacob taught on Monday and facilitated on Tuesday. A complete transfer of instruction took place in the last two sessions when I did not lead the instruction and assumed the role of observer and assistant. When Jacob assumed instruction in Weeks 11 and 12, he facilitated instruction using the same TPK routines I had established earlier (as evidenced in field notes).
Technological pedagogical content knowledge. In making the lab selection I modeled TPCK, which included a subtle knowledge of how to best use technology to teach content. An advanced knowledge of the content, the technology, and how students interacted with the content in the technological environment was necessary. Over time Jacob began to suggest the labs he wanted to use. Discussion focused on my experience with that particular topic and lab, the features of GSP that might require modeling, and possible student errors to watch for (as well as ways to address them quickly). As indicated in the email of October 8, Jacob began to assume the role of selecting labs, which is evidence of his developing level of TPCK. An email I received on October 31 clearly marked a transition of ownership in task selection: “I would like to do the labs on Triangle Angle Sum; Exterior Angles in a Triangle; Triangle Inequalities; pp65-67 (Ch3) [see Bennett, 2002]. … I will be doing the labs on Monday and you on Tuesday.”
Although documenting exactly how Jacob came to this more advanced level of TPCK is impossible, Jacob did achieve this status. Evidence that supports this claim includes the fact that he began to create his own labs for his students. One lab he shared with me was on creating an area formula for a regular polygon. The ability to successfully design and independently facilitate the teaching of a discovery-based lesson with GSP is clearly an indication of a knowledge base found in the intersection of technological knowledge, content knowledge, and pedagogical knowledge.
Implications for Further Research
Success Factors
Replication of a study of this nature is problematic due to the highly personal nature of the interaction between the classroom teacher and me. The following factors seemed to contribute to the success Jacob experienced and should be considered when soliciting teachers for a similarly designed study. Jacob was a veteran teacher and possessed advanced levels of content knowledge, pedagogical knowledge, and pedagogical content knowledge. Jacob was a reflective practitioner as demonstrated in the way he assessed and used student data for further instruction, as well as in the value he placed on observing my instruction with his students.
One external success factor was found in this study: Jacob’s work was supported by school personnel at both the departmental and institutional level. This factor was demonstrated by a collegial attitude extended to me and the fact that I was given a key to the mathematics office. Although this action might seem trivial, a lack of support by colleagues and administrators can be a strong deterrent when attempting change of this magnitude. Also, not trivial, the geometry classes had access to the computer lab on Tuesdays and Wednesdays each week for the majority of the year. Standardized testing was the largest obstacle, since the labs were literally booked solid in the beginning and end of the school year to accommodate state and local assessments.
State standards are interpreted differently by classroom teachers and can be a deterrent from taking the time to do “something else” like integrating technology. As a former classroom teacher and a college supervisor to student teachers, I have over the years observed many classroom teachers using their interpretation of state and local mathematics standards to restrict the curriculum to a lecture-and-drill format with a checklist mentality. Jacob did not exhibit this mentality. He considered the overarching goal of communication and student understanding as well as the specific content objectives cited in the standards. He found GSP to be such a valuable tool that he began to mentor other geometry teachers at the high school in the integration of this technology (personal communication approximately a year later at the state mathematics conference).
The final aspects of Jacob’s personality that may have contributed to the study’s success were his efficacy and beliefs regarding the instructor’s role. Jacob possessed the goal of teaching for understanding and appeared to view mathematics as a process. Jacob was comfortable asking his students questions and guiding them toward the answers. More importantly, he was comfortable asking himself questions regarding his teaching practice, even though he was a veteran teacher assigned to teach precalculus and honors geometry classes.
Each of these success factors can be linked with recommendations made by McDougall (1997). Jacob was given a mentor, his work was supported and valued by the school, he was a reflective practitioner willing to change his teaching practice, and he was willing to share control of the learning environment with students. The only factor missing was release time. The apprenticeship model was sensitive to the lack of release time since the study took place during school time with little intrusion on Jacob’s planning period.
The Apprenticeship Model
The apprenticeship model created in this study was time intensive for me as I was in the high school 1 day a week for approximately 12 weeks (Week 9 was skipped). It was not time intensive for the classroom teacher. In fact, Jacob enjoyed the fact that he could “learn on the job.” One suggestion would be to work with a cohort of teachers in a school or district. Including more teachers in the intervention would create and foster a support network at the research site. The networked teachers would, hopefully, continue the use of technology and become a support for each other upon conclusion of the teacher development experiment.
The use of an apprenticeship model need not be limited to a researcher/teacher pair. Teachers with a more advanced level of TPCK can assume the mentor role following the task selection, teaching, and assessment cycle. Margerum-Leys and Marx (2002) investigated technology knowledge brought into and acquired through student teaching placements by observing student teacher/mentor pairs. In either case, the major benefit of the model is that the mentor relieves the classroom teacher of the cognitive responsibilities of designing and conducting instruction until the teacher understands how the technology works (TK), understands when and how to change the classroom environment (TPK), and understands how to best weave technology and content (TCK) with the goal of providing an appropriate student-learning experience with technology (TPCK).
References
Bennett, D. (1999). Exploring geometry with The Geometer’s Sketchpad. Emeryville, CA: Key Curriculum Press.
Cabri Geometry II. (1996). [Software]. Texas Instruments, Inc.
Chazan, D. (1993). High school geometry student’s justification for their views of empirical evidence and mathematical proof. Educational Studies in Mathematics, 24(4), 359-387.
Chazan, D., & Yerushalmy, M. (1998). Charting a course for secondary geometry. In R. Lehrer & D. Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 67-90). Mahwah, NJ: Lawrence Erlbaum Associates.
Choi-koh, S. S. (1999). A student’s learning of geometry using the computer. Journal of Educational Research, 92(5), 301-311.
Cobb, P., Confrey, J., diSessa, A., Lehrer, R., & Schauble, L. (2003). Design experiments in educational research. Educational Researcher, 32(1), 9-13.
de Villiers, M. (1998). An alternative approach to proof in dynamic geometry. In R. Lehrer & D. Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 369-394). Mahwah, NJ: Lawrence Erlbaum Associates.
Hughes, J. (2004). Technology learning principles for preservice and in-service teacher education. Contemporary Issues in Technology and Teacher Education, 4(3). Retrieved from https://citejournal.org/vol4/iss3/general/article2.cfm
Hughes, J. (2005). The role of teacher knowledge and learning experiences in forming technology-integrated pedagogy. Journal of Technology and Teacher Education, 13(2), 277-302.
Jackiw, N. (2001). The Geometer’s Sketchpad (Version 4) [Software]. Berkley, CA: Key Curriculum Press.
July, R. A. (2001). Thinking in three dimensions: Exploring students’ geometric thinking and spatial ability with the Geometer’s Sketchpad (Doctoral dissertation, Florida International University, 2001). ProQuest Digital Dissertation Database No. AAT 3018479.
Keating, T., & Evans, E. (2001, April). Three computers in the back of the classroom: Pre-service teacher’s conceptions of technology integration. Paper presented at the annual meeting of the American Educational Research Association, Seattle, WA.
Kelly, A. (Ed.). (2003). The role of design in educational research [Themed issue]. Educational Researcher, 32(1). Retrieved from http://www.aera.net/publications/Default.aspx?menu_id=38&id=393
Kelly, A. E., & Lesh, R. A. (2000). Handbook of research design in mathematics and science education. Retrieved from the Questia Web site: http://www.questia.com/PM.qst?a=o&d=24435975
Laborde, C. (2000). Dynamic geometry environments as a source of rich learning contexts for the complex activity of proving. Educational Studies in Mathematics, 44, 151-161.
Lester, M. L. (1996). The effects of The Geometer’s Sketchpad software on achievement of geometric knowledge of high school geometry students. Unpublished doctoral dissertation, University of San Francisco.
Margerum-Leys, J., & Marx, R. (2002). Teacher knowledge of educational technology: A study of student teacher/mentor teacher pairs. Journal of Educational Computing Research, 26(4), 427-462.
Mariotti, M. A. (2000). Introduction to proof: The mediation of a dynamic software environment. Educational Studies in Mathematics, 44, 25-53.
McDougall, D. E. (1996). Mathematics teachers’ needs in computer-based geometric environments. Paper presented at the eighth International Congress on Mathematics Education, Seville, Spain. Retrieved on December 3, 2007, from http://mathforum.org/mathed/seville/mcdougall.html
McDougall, D. E. (1997). Mathematics teachers’ needs in dynamical geometric computer environments: in search of control. Unpublished doctoral dissertation, University of Toronto.
Mishra, P., & Koehler, M. J. (2006). Technological pedagogical content knowledge: A framework for teacher knowledge. Teachers College Record, 108(6), 1017-1054.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
Niess, M. L. (2005). Preparing teachers to teach science and mathematics with technology: Developing a technology pedagogical content knowledge. Teaching and Teacher Education, 21, 509-523.
Niess, M. L. (2006). Guest editorial: Preparing teachers to teach mathematics with technology. Contemporary Issues in Technology and Teacher Education, 6, 1-9. Retrieved from https://citejournal.org/vol6/iss2/mathematics/article1.cfm
Pierson, M. E. (2001). Technology integration practice as a function of pedagogical expertise. Journal of Research on Computing in Education, 33(4), 413-430.
Saye, J. W. (1998). Technology in the classroom: The role of disposition in teacher gatekeeping. Journal of curriculum and Supervision, 13(3), 210-234.
Senger, E. S. (1999). Reflective reform in mathematics: the recursive nature of teacher change. Educational Studies in Mathematics, 37, 199-221.
Shafer, K. G. (2004). Two high school teachers’ initial use of Geometer’s Sketchpad: Issues of implementation (Western Michigan University, 2004). ProQuest Digital Dissertation Database No. AAT3154510.
Shulman, L. S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57(1), 1-22.
Simon, M. A. (2000). Research on the development of mathematics teachers: The teacher development experiment. In A. E. Kelly & R. A. Lesh (Eds.), Handbook in research design in mathematics and science education (pp. 335-359). Mahwah, NJ: Lawrence Erlbaum Associates, Publishers.
Author Note:
This paper is based on dissertation research completed at Western Michigan University under Tabitha Mingus. This work has been presented at the annual conference of the Association of Mathematics Teacher Educators (2007) and at the annual conference of the Society for Information Technology and Teaching (2007).
The author wishes to thank Maggie Niess, Marcia Weinhold, Rose Cavin, and two anonymous reviewers for thoughtful comments on earlier drafts of this article.
Kathryn G. Shafer
Bethel College
[email protected]
![]()