This paper reports on a study of a group of 22 preservice teachers enrolled in a first-semester mathematics teaching methods course. Course activities included participation in two separate field experiences in neighboring school districts. The methods class placed considerable emphasis on the use of advanced digital technologies in the teaching and learning of mathematics, with particularly extensive use of the TI-Nspire. The field experiences varied in the extent to which technology was used, from virtually nil in some classrooms to full implementation in others. The purpose of this study was to examine preservice teachers’ evolving relationships with advanced digital technologies in their teaching, examined through the lens of their technological pedagogical content knowledge (Koehler & Mishra, 2005; Niess 2005, 2006, 2007) and to examine the interplay between their field placements and the quality of their deployment of advanced digital technologies in inquiry-based lessons.
More than two decades of research and experience support the idea that computer and calculator technologies can have an important role to play in supporting and affecting student learning (Blume & Heid, 2008; Heid, 1988; Heid & Blume, 2008; Kaput, 1992; Kutzler, 1996; Papert, 1980; Waits & Demana, 1999; Zbiek, Heid, Blume, & Dick, 2007). Thus, the methods course in which the preservice teachers in this study participated was designed to introduce them to inquiry-based learning with open-ended questioning in a technology-rich environment. The course proceeded from the premise that the use of advanced digital technologies can be a useful method for teaching in such a manner. For example, a typical problem for exploration is the Glass Rod problem: “A glass rod drops and breaks into three pieces. What is the probability that a triangle can be formed from the pieces?”
The preservice teachers use technology to take statistical and geometric approaches to exploring the problem. The problem can be approached in a traditional manner but can be greatly enhanced by, for example, the use of technology to simulate the experiment and visualize the process (Edwards & Phelps, 2008). The preservice teachers then draw on their experiences in classroom observations as well as their own experiences in learning with technology to write reflections on what they consider to be some implications of using this kind of problem in teaching from the point of view of its open-ended nature, assessment, and place in the curriculum.
Based on pilot work and our collective experience, we see that preservice teachers generally fall into three categories with regard to their beliefs regarding the utilization of technology in mathematics classrooms: (a) “Naysayers,” who would like to minimize the use of technology; (b) “Yes-Buts,” who believe that students should learn concepts first and only then have access to technology; and (c) “Yes-Ands,” who believe that technology should be used as an integral part of learning concepts. (See Niess et al., 2009, for a similar, more sophisticated, taxonomy).
Preservice teachers’ relationship to these categories is fluid and can change, perhaps, from topic to topic and because of particular experiences in their trajectory of development as preservice teachers. Nevertheless, the categories are useful as descriptions of the most prevalent dispositions preservice teachers bring to bear in their engagement with advanced digital technologies.
As preservice teachers are developing a teaching identity, the influences that push them in one direction or another can be observed. Most preservice teachers seem to have achieved their own mathematical success by being proficient in traditional environments (especially at the college level where use of technology is often discouraged) and, therefore, tend to be either in the category of Naysayers or Yes-Buts. Educators generally do not fall naturally into the third category without some coaxing, and the methods course was taught in a manner that might persuade the preservice teachers to consider this position.
The data from this study show that the methods class and the field placements served to challenge the preservice teachers to clarify where they stand in this categorization and what they imagine the place of technology to be in their future careers as mathematics teachers.
This small scale study was completed with a limited number of participants and a limited number of cooperating schools, but the principal conclusion of the study is that a crucial, perhaps decisive, effect on candidates’ attitudes regarding the use of advanced digital technologies in their teaching is achieved by modeling exemplary practice in the field placement. That is to say, such modeling creates the possibility that teachers may migrate to the category of Yes-And. Many of the preservice teachers in this study were resistant to the extent of the emphasis on technology in the methods class. With one exception, however, students whose field placements were in schools where technology was used extensively developed positive attitudes to technology.
Not surprisingly, the preservice teachers with positive technology-oriented experiences in the field expressed stronger desires to incorporate technology into their own teaching. The preservice teachers’ experiences in the classroom primed them for the possibilities of technology. The evidence shows, however, that they must experience exemplary practice before they are convinced of the benefits of working to incorporate technology in their own teaching. Frykholm (1998) and Zevenbergen (2005) found a similar relationship between field placements and reform approaches to teaching but without considering technology in their studies.
A secondary conclusion is that while there was a general improvement in the quality of the lesson plans written by the preservice teachers as the semester progressed, the lesson plans written by those students with field placements in technology-rich environments showed more sophistication, not just in the use of technology, but in terms of implementing inquiry-based and open-ended instructional approaches.
Theoretical Context and Related Literature
A growing body of research indicates that digital technologies, including graphing calculators and computer algebra system (CAS) enabled calculators, can enhance young students’ conceptual and procedural knowledge of mathematics (Dunham, 2000; Thompson and Senk, 2001; Zeller & Barzel, 2010). Research has also shown, in particular, the benefits to students of dynamically linked representations (Kaput, 1994; Rich, 1996), for example, when students can see equations and graphs of equations simultaneously with changes to one instantaneously and dynamically reflected in the other.
As technology has become more sophisticated and functionalities of handheld calculators have increased dramatically, research is needed that explores the extent to which teachers are able to employ technology effectively (Koehler & Mishra, 2005; Niess, 2005) and the extent to which students are able to work effectively in such technology-rich environments, which can include graphing calculators, computer algebra systems, and dynamic geometry systems (Edwards, 2004; Geiger, Faragher, & Goos, 2010; Kieren & Drijvers, 2007; Lee, 2005; Meagher, 2007).
Following Shulman’s (1986) seminal analysis of teachers’ knowledge as a complex structure including content knowledge, and pedagogical knowledge and his introduction of the concept of pedagogical content knowledge, most, if not all, research in the area of teacher knowledge has been grounded in his framework. Mishra and Koehler (2006), Koehler and Mishra (2005), and Niess (2005, 2006, 2007) joined other authors in discussing the concept of the technological, pedagogical, and content knowledge (TPACK). Thus, technology-related research in the teachers’ professional development and education field gained a new rich conceptual framework or “an analytic lens for studying the development of teacher knowledge about educational technology” (Mishra & Koehler, 2006, p. 1041).
The TPACK model involves the content knowledge, the pedagogical knowledge, and the technology knowledge required to teach in technology-rich environments (see Figure 1). Furthermore, the TPACK model discusses the combination of basic knowledge such as technological content knowledge (TCK) and technological pedagogical knowledge (TPK). Mishra & Koehler (2006) discussed TCK as follows: “Teachers need to know not just the subject matter they teach but also the manner in which the subject matter can be changed by the application of technology” (p. 1028). On the other hand, “technological pedagogical knowledge (TPK) is knowledge of the existence, components, and capabilities of various technologies as they are used in teaching and learning settings, and conversely, knowing how teaching might change as the result of using particular technologies” (Mishra & Koehler, 2006, p. 1028). Finally, TPACK according to Mishra and Koehler (2006) is
the basis of good teaching with technology and requires an understanding of the representation of concepts using technologies; pedagogical techniques that use technologies in constructive ways to teach content; knowledge of what makes concepts difficult or easy to learn and how technology can help redress some of the problems that students face; knowledge of students’ prior knowledge and theories of epistemology; and knowledge of how technologies can be used to build on existing knowledge and to develop new epistemologies or strengthen old ones (p. 1029).
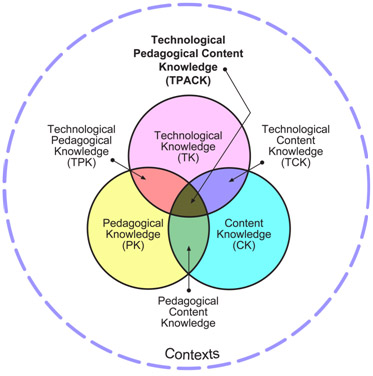
Figure 1. Mishra & Koehler’s TPACK Model (Rights-free image reprinted from http://tpack.org)
Clearly, there is much to consider when studying pre- and in-service teachers’ knowledge, views, beliefs, attitudes, and decisions about the use of technology in their classroom. Niess (2006, 2007) discussed how teachers’ beliefs about teaching mathematics with technology play a crucial role in the development of TPACK. Moreover, Niess (2005) explained that there are four basic components of TPACK:
- An overarching conception of what it means to teach a particular subject such as mathematics integrating technology in the learning.
- Knowledge of instructional strategies and representations for teaching particular mathematical topics with technology.
- Knowledge of students’ understandings, thinking, and learning with technology in a subject such as mathematics.
- Knowledge of curriculum and curriculum materials that integrates technology with learning mathematics. (p. 197)
For the purpose of the analyses in this paper these components can be summarized as conceptions, implementation, students, and curriculum.
Increasingly preservice teachers are asked to incorporate technology into their teaching (International Society for Technology in Education, 2000; National Council of Teachers of Mathematics, 2000; National Council for Accreditation of Teacher Education, 2008). The extent to which they are willing or able to do so is influenced by a number of factors, including their own experience with technology, constraints imposed by their teaching placements, and the quality of their training in the technology (Bullock, 2004; Moursund & Bielefeldt, 1999).
Research Question
Through the use of the TI-Nspire in the methods course, we examined teachers’ relationship to and use of the TI-Nspire and other advanced digital technologies along the following dimensions: (a) the role of technology in the teaching and learning of high school mathematics; (b) the role of inquiry in the teaching and learning of mathematics in technology-rich environments; and (c) the implementation of technology-rich lesson plans/units in classrooms.
Specifically, we examined the preservice teachers’ evolving attitudes regarding the use of advanced digital technologies in teaching and learning mathematics, particularly in relation to the influence of their field placements. We also studied preservice teachers’ design of technology-rich lessons and the extent to which these lessons promoted inquiry and learning for understanding.
Data Collection
The preservice teachers (n = 22) were engaged in routine activities comprising a mathematics teaching methods course that met for two 75-minute sessions a week for 15 weeks at a small midwestern U.S. university. They used the TI-Nspire handheld regularly. The course was designed specifically for preservice secondary school mathematics teachers, with the preservice teachers engaging in activities focused primarily on pedagogical issues (e.g., constructing lesson plans and grading rubrics, creating technology-oriented mathematics activities) and content issues (solving mathematics problems, assessing student work).
The course was the first in a two-course methods sequence, these courses being the preservice teachers’ only methods courses in the program. Prior to taking the methods courses, the preservice teachers took foundations and mathematics content courses. In the course that is the focus of this study, the preservice teachers had two, 2-week field placements. They went to schools individually and were expected to teach two lessons during the field experience as well as observing an experienced teacher. The first field placement was typically in a secondary school (grades 9-12), and the second placement was typically in a middle school (grades 7-8).
Specific activities in the course included the following:
- Field Experience Reports: On two separate occasions, the preservice teachers researched, developed, and implemented mathematics lessons as part of the field teaching component of the class. The first critique focused on student behavior, teacher/candidate interactions, and instructional effectiveness. The second critique focused on problem-posing and analysis of student mathematical thinking.
- Activity Write-Ups: The preservice teachers submitted five secondary-grades mathematics activities that they constructed, either wholly original or modified from preexisting materials. The preservice teachers were encouraged to use these materials in their field component, if possible.
- Graphing Calculator Teaching Project: The preservice teachers conducted original research dealing with the teaching of a secondary mathematics problem or set of related problems using the TI-Nspire graphing calculator. The problem(s) selected for study were subject to instructor approval to be well-suited for study with graphing calculators. The research was designed so that the preservice teachers would meaningfully include the TI-Nspire in the investigation of the problems. They would then teach a class and analyze the results of their teaching.
In addition to the standard activities of the methods class, the preservice teachers completed a Mathematics Technology Attitudes Survey and three short surveys, each of which consisted of a mixture of multiple-choice and open-ended items (administered electronically in weeks 4, 8, and 13 of the study; see Appendix A). Finally they completed an open-ended exit survey with more general questions than those asked in the Week 4, 8, and 13 surveys.
The surveys were developed to be wide ranging in the questions asked of the preservice teachers, falling into four categories: their current philosophy of teaching; their experiences with technology in the class; the interactions among the class, mathematics content, and technology; and their field placements. Of particular interest was the development of the teachers’ dispositions toward the growth in their TPACK as the semester developed. Based on pilot work and experience, we had established the categories of Naysayers, Yes-Buts, and Yes-Ands and looked to develop questions that would shed light on the preservice teachers’ beliefs in regard to these categories. For example, a question such as the following, asked in weeks 4, 8, and 13, allowed us to track the trajectory of the student thinking through the semester as their TPACK developed, both in general and with regard to the four Niess (2005) components, Conception, Implementation, Students, and Curriculum: “Students shouldn’t use calculators until they have thoroughly mastered the required skills by-hand.”
Other questions were designed to ask students explicitly about the use of technology in their field placements and the relationship between the use of technology to promote inquiry-based learning in the classroom and the reality of the field placement. Examples of such questions include, “My field placement this semester has taught me a lot of practical technology skills that I can use,” and “My field placement this semester has made me think more critically about technology than before.”
Of particular importance was administering the surveys at three different stages of the semester so that we could track the development of the preservice teachers’ thinking across the semester. The surveys, field placement reports, and Lesson Plans were coded for the four Niess components. Examples of Conception would be a preservice teacher expressing as yet untried ideas about how technology could be used and how it could be useful in supporting students. With Implementation we were looking, in the first instance, for how preservice teachers were talking about using technology but also looking at whether they manifested the notion of technology supporting known concepts (Yes-And) or of technology used for the development of concepts (Yes-But).
The code Students was used when there was evidence of preservice teachers placing themselves in the position of the student and making that crucial transition that all preservice teachers must make from doers to teachers of mathematics, which switches their focus to students’ understandings, thinking, and learning. The code Students was used for confirming and disconfirming evidence of preservice teachers development along this dimension.
Data Analysis and Discussion
Our analysis of the data focuses on two principal dimensions: (a) the interplay between the effects of the methods class and the field placement on the preservice teachers’ experiences of and attitudes toward technology, and (b) the evolution of the preservice teachers’ lesson plans over the course of the semester. This analysis will be preceded by a look at the preservice teachers’ attitudes toward technology. (It should be noted that all 22 preservice teachers filled out the presurvey, but only 20 were able to fill out the postsurvey due to special arrangements made for two preservice teachers’ final exams, of which the postsurvey was a part.)
General Attitudes Toward Teaching and Learning Mathematics With Technology
The weeks 4, 8 and 13 surveys proved useful in tracking the general attitudes of the preservice teachers to the use of technology with Likert-type (very strongly agree, strongly agree, agree, not sure, disagree, strongly disagree, very strongly disagree) and open-ended questions. The pre- and postsurvey included Likert-type questions (strongly disagree, disagree, agree, strongly agree) addressing this issue.
On the presurvey instrument, 20 of the 22 preservice teachers agreed or strongly agreed that graphing calculators helped them understand mathematics and work on exams. This number changed to 19 out of 20 in the postsurvey. In addition, a clear majority of the subjects agreed or strongly agreed that graphing calculators increased their desire to do mathematics (16 of 22 in the presurvey and 13 of 20 in the postsurvey). These results suggested that a Naysayer attitude was not prevalent among the preservice teachers as they did mathematics. They also suggested that TCK was an area of which they had some knowledge and confidence. In relation to Niess’ (2005) four components, it was not clear from these answers that the preservice teachers had good Conceptions or Implementation knowledge as yet.
Other results in the survey suggest there was a strong leaning in the direction of the category Yes-And at the beginning of the course. For example, 19 of the 22 preservice teachers agreed or strongly agreed at the beginning of the study that graphing calculators are a useful support for discovering algebraic rules and that the graphing calculator is useful because it allows people to look at the same problem in more than one way. These numbers changed to 18 out of 20 and 19 out of 20, respectively, at the end of the study. It was interesting to contrast this conclusion with the lesson plans the teachers wrote. We saw a willingness toward TPACK ideas expressed in the survey but did not see strong evidence of TPACK in the lesson plans, except for those with exemplary field placements. In particular, there seemed to be a disconnect between preservice teachers’ dispositions and their Conceptions and Implementation, as evidenced in the lesson plans they wrote. See Frykholm (1998) and Zevenbergen (2005) for similar disconnects in studies where technology was not part of the study.
However, as the semester progressed and the preservice teachers related the methods course and field experiences to each other, we perceived that the preservice teachers were, perhaps, becoming clearer in articulating where exactly they stood on technology use. For example, 18 of the 22 preservice teachers in the presurvey agreed that graphing calculators help people who have difficulties with algebra to still be able to do mathematics. However, this number changed to 14 of 20 in the postsurvey, suggesting that some preservice teachers were acknowledging a Yes-But perspective.
We saw more of a Yes-But identity in the preservice teachers’ stance that students need to know skills independent of calculator use. Twenty of the 22 preservice teachers in the presurvey and 18 of 20 in the postsurvey stated that they needed to know how to compute because the calculator would not do everything for them. All of them agreed in the pre-and postsurveys that the graphing calculator is a useful tool to check their work both. However, many of the preservice teachers used calculators in the process of working mathematically: 18 of 22 at the beginning of the study and 18 of 20 of them at the end of the study agreed or strongly agreed that the graphing calculator helped them get an idea of the result of a calculation before doing it.
Interestingly, preservice teachers’ attitudes toward teaching and learning mathematics with technology between the beginning of the study and the end of the study were mostly similar except on one item: People who have difficulties with algebra have the same difficulties even with a calculator. Thirteen of the 20 preservice teachers agreed or strongly agreed with this statement in the postsurvey; however, 15 of 22 of them disagreed with this statement in the presurvey. This result suggests the beginning of a transition in this item from a Yes-But to a Yes-And stance. It might serve as evidence that they are thinking more deeply about the Students component (Niess, 2005) of TPACK.
The Interplay Between the Methods Class and the Field Placement
Learning in the Class vs. Learning in the Field
Looking at the general trend (all weeks combined), we observed that the preservice teachers’ university class provided more experience for them in learning technology skills, critical thinking about technology, thinking about the mathematics content, and thinking and working with technology. The field experience, on the other hand, helped them become more reflective in their teaching (see Figure 2). Many preservice teachers agreed that they were learning a lot of practical technology skills that they could use in their methods class sessions (Mean = 5.9) and in their field placement (Mean = 4.7) Most of them also strongly agreed that the methods class activities made them think more critically about technology (Mean = 6.1), suggesting they were moving toward more clearly establishing a position on the use of technology in teaching and learning mathematics.
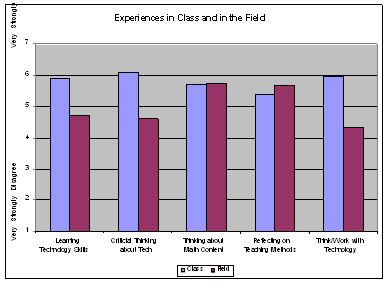 Figure 2. Experiences in class and in the field.
Figure 2. Experiences in class and in the field.
Even though more than half agreed that their field placement also helped them think critically about technology, approximately 8 of 22 of preservice teachers disagreed or were not sure. This result is most likely a reflection of the fact that in many of their placements (particularly the first placement) the preservice teachers were exposed to little or no technology, owing either to the lack of appropriate technology in the schools (often an issue in urban schools) or a lack of interest in the use of technology or ability to use it on the part of the cooperating teacher. This lack of technology meant that the preservice teachers were constrained in their opportunities to build their TPACK skills, in particular, the Implementation and Student components (Niess, 2005). This situation is further reflected in the fact that their class (Mean = 6) was more helpful in requiring them to think and work a lot with technology as they designed teaching activities than was their field placement (Mean = 4.31). Eleven of 20 of the preservice teachers were not sure or disagreed that their field experience helped them to think about technology when they designed activities.
When asked in the open-ended prompts to discuss the technological skills they were learning that would be useful in their future teaching, the preservice teachers’ responses changed over time. At Week 4, 8 out of 20 preservice teachers said that they really liked TI-Nspire calculators expressing sentiments such as follows:
Being able to use the Nspire calculators is extremely cool. We are some of the first people to use these calculators and our experience with them will be invaluable.
We’ve also been exposed to the TI-Nspire calculator. I am amazed by this. The amount of things you can do on this is incredible. However, the thing that appeals to me most about this calculator is that it is something a student can carry around with them. What I mean is that the calculator has features that reflect Microsoft Excel and Geometer’s Sketchpad. For a student to have that access in the classroom that doesn’t have computers would be great.
Two preservice teachers discussed their worries that they were learning about this new technology but it was likely that they would not have access to such calculators when they taught in future. The other technologies they discussed at Week 4 were the Smartboard (n = 8), websites (n = 4), and Geometer’s Sketchpad (n = 1). However, by Week 8, no one discussed TI-Nspire calculators. Many of them were discussing the little access they had to advanced technology in the field: “After going out in the field, I believe more than I did before that the technology I am learning to base my lessons with, though, is far too advanced.” Many students reported exploring free resources that the Internet offers. Arguably, not having a supportive field component meant that the preservice teachers lacked the opportunity to engage with the Implementation and Student components (Niess, 2005) of TPACK and caused the preservice teachers to question their Conception component.
The Influence of the Field Placement
The field placements became an arena where, depending on the use of technology in the particular classroom, the preservice teachers either had an opportunity to move beyond developing their Conception component (Niess, 2005) of TPACK to a deeper engagement with the Implementation and Student components or to leave the Implementation and Student components undeveloped, fostering regression in their Conception component. In some of the field placements little or no technology was used by either the cooperating teacher or the preservice teacher. Other field placements were technology rich. For example, in one field placement the preservice teacher observed students studying solid geometry by constructing sketches in Geogebra, posting them on course Wikispaces pages, and creating podcasts explaining their work and sharing it for feedback and discussion with classmates.
Responses on the open-ended exit survey show a direct relationship between the preservice teachers’ field placements and their dispositions to the use of technology in the future. Furthermore, the Lesson Plans indicated a direct relationship between the quality not only of the technology but also of inquiry-based approaches in the work of the teachers with technology-rich placements. Despite the emphasis placed on technology in the methods class, half of the students whose field placements had minimal or no technology did not develop a positive attitude to the use of technology in the teaching and learning of mathematics.
One preservice teacher who commented, “I found that my field teachers did not use technology in their classroom. I found their teaching methods to be more practical, and I will probably lean more towards their style,” had also said, “I found the TI-Nspire to be too complicated and not worth the hassle figuring it all out. I spent more time trying to figure out how to use it than I did learning about math.”
On the other hand, all but one of the preservice teachers who had been exposed to exemplary practice in technology-rich environments were eager to incorporate technology in their future practice. One student commented, “My two field experiences were on different ends of the technology spectrum. One school barely had any technology and the other school had a lot.” These two experiences resulted in this student declaring, “I am now more likely to use technology in my teaching. Technology offers so many advances for students and can relate to many different learning styles.” Another student commented, “I will definitely want to use technology,” having been in a school where “there was a grant for TI-89s in one class, for laptops in another and…their teacher was proficient in all of these technologies.” These experiences provided these preservice teachers the opportunity to experience the Implementation and Student components (Niess, 2005) of TPACK.
It can be difficult for the students to make the connection between the practices developed and encouraged in their methods classes without exemplary experiences in classrooms of how these ideas can be put into practice. The students who made comments such as, “I am less likely because of un-user friendly the TI-Nspire was,” were students who did not see the TI-Nspire being used in a classroom. This direct relationship between the development of a positive disposition toward teaching with technology and exemplary experiences in a technology-rich environment calls for the development of a closer school-university partnership to allow students to make meaningful connections between their methods classes and the reality of classrooms. This is further evidence that students were primed with a certain sophistication and development with ideas from all components of TPACK, especially the Conception component, in their Methods class but their ability to consolidate and implement these ideas was sensitive to the field placements, both in terms of their willingness to implement good practice in using technology and their ability to implement good practice.
We observed some hardening stances on the Yes-But/Yes-And axis in the Week 13 survey. Looking at the data across the weeks, approximately 70% of the preservice teachers stated that they would like to use, specifically, the TI-Nspire when they became full-time teachers. However, on the more general question of the place of technology in the mathematics classroom, approximately 70% of the preservice teachers agreed that students should not use calculators until they have thoroughly mastered the required skills by hand.
Instructional Practice and the Relationship Between Teaching Methods, Content, and Technology
It was interesting to observe differences in how the preservice teachers thought about technology for their own use in learning mathematics and what they thought was appropriate for their students. This was a crucial distinction between TCK and TPACK, particularly in the Implementation and Student components (Niess, 2005). In the presurvey, a majority of the participants agreed that graphing calculators help them understand mathematics, work on exams, and increase their desire to do mathematics. However, an analysis of the preservice teachers’ statements about instructional practice show the Yes-But camp holding sway. One preservice teacher characterized this stance by arguing,
When kids are younger and inexperienced, they need to be taught the basics using direct instruction like I was. Now that I know some things, I can use the calculator to learn more. But I have a good foundation in the basics FIRST.
Some were in the Yes-And camp; for example one preservice teacher argued that
technology can make it easier to test conjectures. For instance, with Sketchpad, we can test countless conjectures much more quickly than possible when using pencil and paper. When we observe behaviors in Sketchpad (or with the Nspire), students are more motivated to ask “does this always happen?”
However, reservations about technology were more prevalent. The Yes-But approach was all but defined by the preservice teacher who commented, “Technology doesn’t change the way kids learn math. They have to learn it the way I learned it, by repetition and practice.” Another preservice teacher characterized this attitude, stating,
Kids learn the alphabet song to memorize the letters. They use PEMDAS to memorize order of operations. They memorize FOIL BY HAND to learn about multiplication in algebra. After kids learn HOW…then they are in a position to learn WHY.
Some preservice teachers saw the use of technology as challenging the current curriculum.
Technology does change the content. There are things that I studied in school that don’t seem relevant in algebra class anymore. For instance, factoring. We did an assignment on the Nspire that showed that 99% (or more) of quadratics aren’t factorable. So why do we spend all of this time factoring?
This attitude was, however, something of an anomaly. An overarching Yes-But attitude went through much of the preservice teachers’ responses. There is strong evidence of a philosophical disposition that the teaching and learning of mathematics should precede any use of technology, and while technology can be useful, it is not imbricated with teaching and learning. As one preservice teacher put it, “I’m not convinced that technology should influence content taught or pedagogy. But I do think that the content and pedagogy should influence technology.”
Lesson Plans
Lesson plans were written by the students at four different stages in the semester: two before their field placements, one between the first and second field placements, and one in conjunction with the second field placement. The lesson plans were scored along three dimensions:
- Implementation of Technology. Active (1), Neutral (0), Passive (-1)
- Implementation of Inquiry-Based Methods (adapted from Northwest Regional Educational Library (Northwest Regional Educational Laboratory, 1997). Student initiated (1), Guided inquiry (0), Structured Inquiry (-1)]
- Quality of Problem Solving. Active (1), Neutral (0), Passive (-1)]. (See Appendix B for full rubric)
In the case of Implementation of Technology, the difference between passive and active was whether the task could be done without technology; that is, is the technology a necessary and active part of the task? The development of the Implementation of Technology section was particularly influenced by Niess’s (2005) description of the components of TPACK, such as “knowledge of instructional strategies and representations for teaching particular mathematical topics with technology” (p 197).
Each of the lessons was scored and the mean averages score across the 20 preservice teachers calculated (see Table 1). Analysis of the scores showed that the students struggled along all three dimensions but improved in all three areas as the semester progressed.
Table 1
Mean Scores (n = 20) for Each Lesson Plan in the Semester
Technology | Inquiry | Problem Solving | |
| Lesson 1 | -0.25 | -0.5 | 0.25 |
| Lesson 2 | -0.5 | -0.375 | 0.125 |
| Lesson 3 | -0.25 | -0.125 | 0.5 |
| Lesson 4 | -0.125 | -0.375 | -0.125 |
| Lesson 5 | 0 | -0.25 | 0.375 |
The first two sets of lesson plans were generally poor and reflected the fact that novice preservice teachers constructed the materials. The second set shows some improvement over the first but were still teacher centered. Several of the lesson plans explicitly used language such as “the teacher will lead students…” In most of these lessons, technology still seemed like an afterthought for most preservice teachers, an add-on rather than a tool to drive instruction and facilitate learning as opposed to reinforcing concepts. The third set of lesson plans, while far from high quality, show marked improvement over the first two sets. This improvement highlighted the growing experience of the students and reflects the fact that these lessons were written after the first field placement.
The preservice teachers’ use of technology was slow to develop, and before the second field placement the use of technology in the lesson plans was unsophisticated. For example, in the set of lessons focused on the Pythagorean Theorem, most of the preservice teachers required students only to draw a particular instance of a problem rather than using the Dynamic Geometry system (DGS) to generalize or form conjectures based on many cases. In the set of lesson plans where the use of technology was optional, several preservice teachers chose not to use technology at all, while others suggested the use of technology for “high level kids only.” Those who employed technology in their lesson plans tended to focus on what buttons to press rather than on rich opportunities for student discovery.
On Lesson 5 a sharp improvement in the preservice teachers’ scores occurred. At one level this improvement was unsurprising, as one might expect the preservice teachers to mature and improve as the semester progressed. A more significant factor may have impacted them at this point, however: the second field placement during which Lesson 5 was written. This thesis is supported when the scores for the lesson plans are disaggregated into two groups (see Table 2): those who had a minimal technology second field placement (MT) and those who had a technology-rich second field placement (TR):
Table 2
Disaggregated Mean Scores (n = 20) for Each Lesson Plan in the Semester
Technology | Inquiry | Problem Solving | ||||
MT | TR | MT | TR | MT | TR | |
| Lesson 1 | -0.25 | -0.25 | 0 | -0.5 | 0 | 0.5 |
| Lesson 2 | 0 | -0.75 | -0.25 | -0.5 | 0.25 | 0 |
| Lesson 3 | -0.25 | -0.25 | 0 | -0.25 | 0.5 | 0.5 |
| Lesson 4 | 0 | -0.25 | -0.25 | -0.5 | 0.25 | -0.5 |
| Lesson 5 | -0.25 | 0.5 | -0.5 | 0 | -0.125 | 1 |
The lesson plan scores for both sets of teachers were similar for the first four lessons. In Lesson 5 the teachers in technology-rich field placements scored much higher in the use of technology, which is to be expected, but significantly, they scored higher in Implementation of Inquiry Based Methods and much higher in Quality of Problem Solving. In the presence of technology, they developed more pedagogically sound activities, and their TPK and TPACK skills were clearly developing. While all the preservice teachers had some development of the Conception component of TPACK, some were able to use the experiences of the class as a springboard to develop strongly in the Implementation and Students components of TPACK.
A significant feature of the lesson plans written in the technology-rich environment is that the tasks were formulated so that the use of technology was a necessary component of the lesson; that is, the tasks were designed assuming an ability and access to use technology, showing some preservice teachers reaching an Implementation level. For example, one preservice teacher designed a lesson centered around the classic birthday problem (the probability that there are two members of a group who share a birthday) involving the use of repeated trials of a simulation on the graphing calculator. Conducting a significant number of trials would be difficult, if not impossible, to replicate in a classroom without technology. Another candidate posed a problem to students involving systems of inequalities. In the lesson, students attempted to construct a closed region satisfying the following constraints using TI-Nspire:
- The system includes at least four linear inequalities.
- The graph of the system generates a closed region.
- At least one pair of lines in the system is perpendicular.
- Every line has to have slope (i.e. not zero or undefined slope).
This lesson was markedly richer than this preservice teacher’s previous lesson plans, not only in the use of technology but in terms of inquiry-based teaching and problem solving.
We argue that an important element in the preservice teachers’ developing calculator active tasks, perhaps becoming Yes-Ands, may have been their placement in a technology-rich environment. The modeling of exemplary practice and the mentorship available to them was likely significant in this move. One of many of the preservice teachers who felt the significance of this placement commented in his field report,
Overall, this class [i.e., the field placement class] had many students eager to work with the new technology. It was exciting to enter the classroom at a point when new and innovative techniques are being introduced and see the results the calculators had not only on the willingness of students to engage in the material, but also on their abilities to construct good solutions to challenging problems. I hope that more students will have access to this new technology in the future to fuel new mathematic interest, just as the Nspires did for the students in Mr. C’s class.
Thus, this particular placement allowed him to see effective implementation of technology and how students work in such an environment and, therefore, developed his own Implementation and Student components of TPACK.
Technology in Task Design
It is interesting to compare the analysis of the lesson plans with the preservice teachers’ survey responses, particularly with regard to the extent they were thinking and working with technology as they designed activities. Several preservice teachers mentioned and complained that the use of TI-Nspire was required at Week 4. However, others stated that they liked working with TI-Nspire and its capabilities; for example,
I have been able to incorporate things such as the TI-Nspire and GSP into my activity write-ups, and I think that incorporating these types of technology into lessons helps to make them more multifaceted and thus easier for a larger percentage of the students in a classroom to understand.
Again, this preservice teacher was considering students’ learning with the help of technology; hence, she was reflecting on her TPK. Two preservice teachers expressed how working with technology made a change in their desire to use technology more in their activity write-ups, showing some development in the Implementation component. One preservice teacher wrote, “I am using technology because we are required to do so. However, the second activity write-up used the TI-Nspire extensively because I thought it would be really neat to see if I could use it for my idea.”
The other student went even further: “At first, the activity seemed to me that we had to use and had to incorporate technology in our activity. Now is seems that technology is more of a tool to help us design a really good hands on, visual activity.”
Many preservice teachers said that they were not learning about mathematics content as they designed activities. However, one preservice teacher mentioned that he was focusing on the “why” question more:
I feel as though I am not learning new mathematics content, but instead, I am thinking of what I already know in a different light. The class has caused me to think more about the why than the how, and to me, that is, the most important element of being a mathematics teacher.
This preservice teacher was reflecting on interaction between the mathematics content and the technology, that is, the TCK component of the TPACK model.
When preservice teachers were asked to discuss the pedagogical issues as they designed activities at Week 4, only two preservice teachers mentioned the use of technology, one mentioning TI-Nspire and the other websites. Other than those two references, they mainly discussed the use of manipulatives, inquiry, problem solving, differentiation, and so on. After having some field experiences at Week 8, one preservice teacher discussed how students were dependent on calculators for computation. Another preservice teacher questioned her ability to use technology in the classroom:
Our assignments have required us to determine how to incorporate the use of technology in the lesson…In doing this, one of the issues I’ve struggled with is the extent we would use technology. A number of cases in using technology have required extensive knowledge/experience with the technology. My question is whether we will practically get students to that level of proficiency where a piece of technology can be used. An even bigger question is whether students would have this technology available to them. My first field experience had no capability for students to use any sort of technology beyond a poorly designed calculator.
The preservice teachers had, of course, seen many activities in the methods class by this stage that showed the possibilities for advanced digital technologies in the class, but without a model of exemplary practice this preservice teacher was struggling with how he could actualize this practice.
Evolving Attitudes and Views Over Time
To complete the analysis we looked at preservice teachers’ responses over time and observed that they strongly agreed that their methods class provided experiences in learning technology skills, thinking about mathematics content, and thinking and working with technology at the beginning (Week 4) and at the end (Week 13), but only agreed at Week 8 (see Table 3). However, the effect of their methods class on critical thinking about technology followed the increasing trend throughout the weeks.
Conversely, the preservice teachers agreed that their field placements helped them in learning technology skills and critical thinking about technology at Week 8, but they were not so sure at weeks 4 and 13. Results of one-way ANOVA showed that there were significant differences among the 3 weeks for the methods class helping them: learning technology skills, F(2,41) = 4.38, p < .05 , thinking and working with mathematics content, F(2,41) = 3.456, p < .05, and teaching methods, F(2,41) = 4.08, p < .05. The sharp decrease in Week 8 might have caused those significant differences.
When the preservice teachers were asked to compare the effect of the methods class and the field placement in how much each of these venues helped them in thinking about interactions between technology, mathematics, and teaching methods, they responded that their university class helped them to consider those interactions more than their field placement (see Table 3). From Week 4 to Week 8, there was an increasing trend in both the university class and the field placement helping them to think about those interactions. However, at Week 13 they did not agree as strongly that their class and field placement helped them to think about interactions between teaching, technology and mathematics (see Table 3). These differences are somewhat difficult to account for but may arise because some of the field placements were not technology-rich and did not provide the preservice teachers an ample opportunity to consider interactions among technology and teaching. This conclusion would further reinforce our argument about the crucial effect of the field placement on the preservice teachers’ experiences.
Table 3
Preservice Teachers’ Attitudes and Views over Time
Venues | Class | Field | ||||
Week 4 | Week 8 | Week | Week 4 | Week 8 | Week | |
| Experiences in the Class and the Field | ||||||
| Learning Technology Skills | 6.15 | 5.40 | 6.22 | 4.65 | 5.00 | 4.44 |
| Critical Thinking about Technology | 6.00 | 6.07 | 6.33 | 4.45 | 5.00 | 4.44 |
| Thinking about Math Content | 6.00 | 5.20 | 6.11 | 5.85 | 5.80 | 5.56 |
| Reflecting on Teaching Methods | 5.55 | 4.80 | 6.11 | 5.80 | 5.73 | 5.33 |
| Think/Work with Technology | 6.05 | 5.80 | 6.22 | 4.50 | 4.00 | 4.44 |
| Interactions among Technology, Mathematics and Teaching | ||||||
| Technology & Math Content | 5.65 | 5.93 | 5.22 | 4.53 | 4.93 | 4.11 |
| Teaching & Math Content | 5.58 | 6.00 | 5.33 | 5.55 | 5.80 | 4.56 |
| Teaching & Technology | 5.47 | 5.80 | 5.44 | 4.68 | 5.40 | 4.22 |
| Teaching Philosophy | ||||||
| Would Like to Use Nspire in Future | 4.84 | 5.13 | 4.89 | |||
| Need to Know Enough Math | 4.21 | 4.73 | 4.89 | |||
| Knowing Why More Important | 5.00 | 5.40 | 4.56 | |||
| Use Calculators After Mastering the Skills by hand | 5.05 | 6.13 | 4.00 | |||
| Seeing More than One Way Confuses Students | 3.11 | 3.20 | 3.67 | |||
Similarly, the preservice teachers agreed that they would like to use TI-Nspire in their future teaching at Week 8 but were not sure or only agreed at weeks 4 and 13. From Week 4 to Week 13 they increasingly agreed that they needed to know enough mathematics to answer all of their students’ questions. They also agreed that students should not use calculators until they have thoroughly mastered the required skills by hand at Week 4 and strongly agreed with that statement at Week 8; however, they were not sure about that at Week 13 (see Table 3). Changes in their level of agreement with this statement over three weeks, resulted in significant difference among 3 weeks, F(2, 40) = 6.55, p < .05. This result shows that by the end of the course there was a growing Yes-And attitude to technology.
Conclusions and Future Directions
The overall conclusions of this study are that (a) if preservice teachers are to develop a positive attitude to the use of advanced digital technologies in their instructional practice, they require more than a methods class to develop TPACK and that modeling of exemplary practice in the field placement has a crucial, perhaps decisive effect on their attitudes and (b) that the most significant improvement in the quality of the preservice teachers’ lesson plans, in terms of being inquiry based and open ended, came when they had field placements in technology-rich environments.
More broadly the implications of the research point to the limitations of stand-alone methods classes in the development of preservice teachers along a trajectory leading them to implementing inquiry-based lessons in their classes and, in particular, using technology to implement inquiry-based approaches. The field placements associated with the methods class can have a decisive effect on whether this trajectory is consolidated and deepened or, on the deficit side, abandoned or left underdeveloped. Developing consonance between methods classes and field placements is a considerable burden given the practical logistics of field placements. However, this consonance can be of such importance that exploring facilitating mechanisms is tremendously important.
One possible such mechanism and a possible avenue of future research would be the development of school-university partnerships so that preservice teachers can engage in the following learning cycle: (a) A class of preservice high school teachers will work with the TI-Nspire to develop lessons or short units designed for technology-rich environments; (b) experienced in-service teachers will review the lessons or short units and present an initial redesign; (c) the in-service teachers will teach the lessons, observed by the preservice teachers; (d) the preservice teachers and in-service teachers will meet together to reflect on and redesign the lesson based on their experiences in the classroom.
Engagement in such a cycle allows preservice teachers to gain the benefit of exemplary practice in task design and the use of advanced digital technologies, focusing them on this aspect of practice without having to deal with early pedagogical aspects that arise from teaching the class themselves (i.e., classroom management, questioning, etc.). The implementation of such a cycle in conjunction with a methods class would allow preservice teachers to develop a more inquiry-based approach to their teaching and to see how the use of advanced digital technologies can facilitate that approach. Such an approach would also be consonant with the theoretical approaches to TPACK as outlined in the research literature (Mishra & Koehler, 2006; Niess, 2006). It would provide a coherent experience for all preservice teachers in which they would see exemplary use of technology, and would provide a much greater chance that preservice teachers would engage with Niess’ basic components of TPACK, namely integrating technology into the teaching of a subject, experiencing exemplary instructional strategies for teaching with technology, and having the opportunity to investigate preservice teachers’ understandings and thinking when learning with technology.
Regardless of the mechanism, our research clearly implies that fruitful mechanisms for integrating the joint experience of methods classes and field placements holds considerable potential value for consolidating issues around inquiry-based approaches and the effective integration of advanced digital technologies in the development of preservice teachers’ PCK and TPACK skills, such as considering mathematics learning from a student perspective and using technology for the development of mathematical concepts.
References
Blume, G.W., & Heid, M.K. (Eds.). (2008). Research on technology and the teaching and learning of mathematics: Volume 2. Cases and perspectives. Charlotte, NC: Information Age.
Bullock, D. (2004). Moving from theory to practice: An examination of the factors that preservice teachers encounter as the attempt to gain experience teaching with technology during field placement experiences. Journal of Technology and Teacher Education, 12(2), 211-237.
Dunham, P. H. (2000). Hand-held calculators in mathematics education: A research perspective. In E. Laughbaum (Ed.), Hand-held technology in mathematics and science education: A collection of papers (pp. 39-47). Columbus, OH: Teachers Teaching with Technology College Short Course Program at The Ohio State University.
Edwards, M. T. (2004). Novice algebra students may be ready for CAS but are CAS tools ready for novice algebra students? International Journal of Computer Algebra in Mathematics Education 10(4), 265-278.
Edwards, M. T. & Phelps, S. (2008). “Can you fathom this? Connecting data analysis, algebra, and geometry with probability simulation.” Mathematics Teacher , 102(3), 210-216.
Frykholm, J. A. (1998). Beyond supervision: Learning to teach mathematics in a community. Teaching and Teacher Education, 14(3), 305–322.
Geiger, V., Faragher, R., & Goos, M. (2010). CAS-enabled technologies as ‘agents provocateurs’ in teaching and learning mathematical modeling in secondary school classrooms. Mathematics Education Research Journal, 22(2), 48-68.
Heid, M.K. (1988). Resequencing skills and concepts in applied calculus using the computer as a tool. Journal for Research in Mathematics Education, 19, 3-25.
Heid, M.K., & Blume, G.W. (Eds.). (2008). Research on technology and the teaching and learning of mathematics: Volume 1. Research syntheses. Charlotte, NC: Information Age.
International Society for Technology in Education. (2000). National educational technology standards for teachers. Eugene, OR: Author.
Kaput, J. (1992) Technology and mathematics education. In (D. Grouws, Ed.) A handbook of research on mathematics teaching and learning (pp. 515–556). New York, NY: Macmillan.
Kaput, J. (1994). The representational roles of technology in connecting mathematics with authentic experience. In R. Biehler, R. W. Scholz, R. Strasser, & B. Winkelman (Eds.), Didactics of mathematics as a scientific discipline, (pp . 379-397). Dordrecht, Netherlands: Kluwer Academic Publisher.
Kieran, C., & Drijvers, P. (2007). The co-emergence of machine techniques, paper-and-pencil techniques, and theoretical reflection: A study of CAS use in secondary school algebra. International Journal of Computers for Mathematical Learning, 11, 205-263.
Koehler, M. J., & Mishra, P. (2005). What happens when teachers design educational technology? The development of technological pedagogical content knowledge. Journal of Educational Computing Research, 32(2), 131-152.
Kutzler, B. (1996). Improving mathematics teaching with DERIVE. Bromley, UK: Chartwell-Bratt.
Lee, H. S. (2005). Facilitating students’ problem solving in a technological context: Prospective teachers’ learning trajectory. Journal of Mathematics Teacher Education, 8, 223-254.
Meagher, M. (2007, June). Response to “Towards relating procedural and conceptual knowledge.” Paper presented at the fifth annual Computer Algebra in Mathematics Education (CAME) Conference, Pécs, Hungary.
Mishra, P., & Koehler, M. J. (2006). Technological pedagogical content knowledge: A framework for teacher knowledge. Teachers College Record, 108(6), 1017-1054.
Moursund, D. G., & Bielefeldt, T. (1999). Will new teachers be prepared to teach in a digital age? A national survey on information technology in teacher education. Eugene, OR: International Society for Technology in Education.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
National Council for the Accreditation of Teacher Education. (2008). Professional standards for the accreditation of teacher preparation institutions. Retrieved from http://www.ncate.org/Standards/tabid/107
Niess, M. L. (2005). Preparing teachers to teach science and mathematics with technology: Developing a technology pedagogical content knowledge. Teaching and Teacher Education, 21, 509-523.
Niess, M. L. (2006). Guest editorial: Preparing teachers to teach mathematics with technology. Contemporary Issues in Technology and Teacher Education, 6(2), 195-203. Retrieved from https://citejournal.org/vol6/iss2/mathematics/article1.cfm
Niess, M. L. (2007, January) Professional development that supports and follows mathematics teachers in teaching with spreadsheets. Paper presented at the 11th annual conference of the Association of Mathematics Teacher Educators, Irvine, CA.
Niess, M. L., Ronau, R. N., Shafer, K. G., Driskell, S. O., Harper S. R., Johnston, C., Browning, C., Özgün-Koca, S. A., & Kersaint, G. (2009). Mathematics teacher TPACK standards and development model. Contemporary Issues in Technology and Teacher Education [Online serial], 9(1). Retrieved from https://citejournal.org/vol9/iss1/mathematics/article1.cfm
Northwest Regional Educational Laboratory. (1997). Inquiry strategies for science and mathematics learning: It’s just good teaching. Retrieved from http://educationnorthwest.org/webfm_send/748
Papert, S. (1980). Mindstorms: Children computers and powerful ideas. New York, NY : HarperCollins.
Rich, K. A. (1996). The effect of dynamic linked multiple representations on students’ conceptions of and communication of functions and derivatives. (Doctoral dissertation, University of New York at Buffalo, 1995). Dissertation Abstracts International, 57(1), Z142.
Shulman L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher 15(2), 4-14.
Thompson, D., & Senk, S. (2001). The effects on curriculum on achievement in second year algebra: The example of the University of Chicago School Mathematics Project. Journal for Research in Mathematics Education, 32, 58-84.
Waits, B. K., &Demana, F. (1999). Calculators in mathematics teaching and learning: Past, present, and future. In E. Laughbaum (Ed.), Hand-held technology in mathematics and science education: A collection of papers (pp. 2-11). Columbus, OH: The Ohio State University.
Zbiek, R.M., Heid, M.K., Blume, G.W., & Dick, T.P. (2007). Research on technology in mathematics education: A perspective of constructs. In F.K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 1169-1207). Charlotte, NC: Information Age Publishing.
Zeller, M., & Barzel, B. (2010). Influences of CAS and GC in early algebra. ZDM Mathematics Education, 42, 775–788
Zevenbergen, R. (2005). Primary preservice teachers. Understandings of volume: The impact of course and practicum experiences. Mathematics Education Research Journal, 17(1), 3-23.
Author Notes
The research reported in this paper was partially supported by Texas Instruments, Inc.
Michael Meagher
Brooklyn College – CUNY
email: [email protected]
S. Aslž Özgün-Koca
Wayne State University
email: [email protected]u
Michael Todd Edwards
Miami University of Ohio
email: [email protected]
Appendix A
Download (pdf)
Appendix B
Download (pdf)
![]()