Using Supported Video Exemplars for the Professional Development of Preservice Elementary School Teachers

Introduction and Theoretical Framework

Videotaped class sessions have been used (Davis, Maher, & Martino, 1992; Schmidt, McKnight, & Raizen, 1996) as instruments of professional development, along with the use of other forms of technology to further mathematical understanding (Olive, 2002; Papert, 1980; Tzur, 1999). This research specifically shares the use of support software that furthers the development of the pedagogical knowledge of preservice elementary school teachers who typically find it difficult to hone in on the underlying features of the targeted practices displayed in the swift-moving action of the classroom being observed.

The videos of the Third International Mathematics and Science Study (TIMSS; Schmidt et al., 1996), in particular, have contributed to the development of understanding of the teaching of mathematics on an international level. Additionally, other researchers (Bulgar, 2002; Fosnot & Dolk, 2001, 2002; Powell, Francisco, & Maher, 2003; Tarlow, 2004; Warner & Schorr, 2004) have used such videotaped class sessions as tools to deepen the understanding of ways children learn mathematics. However, the fine-grained analysis of the data utilized in these more recent studies may not be practical for most classroom teachers or preservice teachers.

For example, the Private Universe Project in Mathematics (Harvard-Smithsonian Center for Astrophysics, 2001) includes a video series (now available through the Annenberg/CPB foundation at http://www.learner.org/resources/series120.html) that uses videotape of mathematics classrooms to promote discussion among groups of teachers gathered to improve their practice of teaching mathematics by carefully analyzing the ways children form and articulate ideas about mathematics. The videotape series is also commonly used to promote pedagogical learning with preservice teachers. Although student artifacts and additional reading opportunities accompany this series, these supports are separate entities. Similarly, the book Connecting Mathematical Ideas: Middle School Video Cases to Support Teaching and Learning (Boaler & Humphreys, 2005) is accompanied by compact disks containing the video vignettes under discussion in the book. These compact disks have independent screens that are supportive of viewing the classroom scenes and include guiding questions and discussion prompts that can assist viewers in understanding the vignettes.

When these types of support resources have been used in my university teacher preparation classes, the preservice teachers often indicate that they are unable to grasp all of the essential elements of the teaching experience while viewing the classroom scenes. They claim they have difficulty in determining specifically where to focus their attention. Determined to address these areas of concern, I developed supports to facilitate the improvement of teaching while observing videotaped classroom episodes of teaching mathematics.

A Web site resource called Virtual Learning Community (VLC) was designed with a specific software component, referred to as MathStore. The distinctive structure of MathStore, within the VLC, integrates supports directly into the video observation such that these supports can be viewed concurrently with the vignettes of the teaching and learning of mathematics. Of interest in this research is the level of engagement and enhanced learning provided by this integration. In particular, preservice teachers’ understanding of affect, mathematical representations, mathematical communication/discourse, and engagement were examined as they observed classroom vignettes incorporating the MathStore feature in the VLC.

Theoretical Framework for Analysis

A models and modeling perspective guided all aspects of this research. Briefly stated, a model can be considered to be a way to describe, explain, construct, or manipulate an experience, or a coordinated variety of experiences (Schorr & Koellner-Clark, 2003). People interpret a situation by mapping it into their own internal model, which helps them make sense of the situation. Once the situation has been interpreted into the internal model, transformations, modifications, extensions, or revisions within the model can occur, which in turn, provide the means by which people can make predictions, descriptions, or explanations for use in the situation at hand. For junior-level preservice teachers, the models internalized regarding the teaching and learning of mathematics are based largely upon their own school experiences and do not always reflect the best of current practice.

It has been documented that people do not make alterations in their internal models through passive transmission, but instead need active, structured experiences (Schorr & Lesh, 2003). Fundamental to this approach is the persistence of internal models, or explanatory systems, that often are not easily modified when attempting to make sense of a situation. Therefore, a key aspect of this research involved using scaffolded video vignettes to stimulate the revision of the preservice teachers’ models for teaching mathematics to increase the likelihood that they might teach in ways consistent with the standards set forth by the National Council of Teachers of Mathematics (NCTM, 2000). To this end, the following research questions were investigated:

• How do preservice teachers interpret the mathematical activity in classrooms observed through the use of supported videotaped vignettes? More specifically, how are preservice teachers able to interpret children’s reactions to tasks;
• How do they communicate their understanding about the nature and use of representations in the classrooms;
• How do they demonstrate what they understand about the nature of the classroom discourse;
• How do they account for the interest and sustained engagement of the children?

Methods and Procedures

Subjects, Setting, and Background

The subjects in this study were undergraduate preservice teachers (PSTs) enrolled in two sections of the Methods of Teaching Mathematics in the Elementary School course at a small private university in New Jersey. Typically, this course is taken at some time during the junior year; hence, most of the PSTs were between the ages of 20 and 22. However, during the semester of this study, there were two nontraditional students: one, a young married mother in her early 30s; and the other, a married father in his 40s who was changing careers. There were a total of 34 PSTs: 17 (16 females and 1 male) in each section. Each section worked independently, and the results were not shared across sections. All PSTs enrolled in the course during this study were full-time undergraduate students who were majoring in education. In the state of New Jersey, students who major in education must also have a second major in liberal arts. Within this particular group of students, there were none majoring in either mathematics or science.

The PSTs were experiencing their first formal instruction regarding the teaching and learning of mathematics in the elementary school. Not only were they expected to develop the necessary teaching skills, but in many cases the PSTs were also required to dispel their notions of a conducive mathematics classroom environment based upon their own robust internal models. Many of the PSTs expressed a fear of teaching mathematics. Throughout the semester, they expressed how their histories as students of mathematics had resulted in feelings of inadequacy as mathematics students. They shared fears that they did not have the ability to teach mathematics. So strong were these fears that many of the PSTs claimed no desire to teach above first or second grade.

For this study, the PSTs observed video vignettes of the teaching of mathematics in a second-grade elementary classroom. The vignettes were part of a VLC Web site, the design of which was funded by a New Jersey State Department of Education grant. The VLC was created to support novice teachers and teacher mentors, as well as preservice teachers, while student teaching and taking methods courses (Fraivillig, Wish, & Bulgar, 2004). The VLC brings together, virtually, six groups serving across the continuum of the practice of teaching: university faculty members, school administrators, veteran teachers, novice teachers, student teachers, and PSTs taking methods courses in mathematics and science. All work produced by the PSTs in this study was completed as a part of their regular university course experience. Although this paper addresses only one aspect and one of the six components of the educational community (PSTs taking a methods courses in mathematics) participating in the VLC, all members of the educational community had access to the video exemplars and the associated supports.

Data

The data examined for this study consist of authentic undergraduate student work related to the project. Data samples consist of the answers to four questions about the vignettes. These questions were embedded in the software and could be read while observing the vignettes.

Project Design

The fundamental purpose of the VLC is to provide high-tech support for the continuum of professional development for teachers of science and mathematics. Users can electronically discuss issues related to teaching and share experiences and support using this Web-based tool. The online community complements the face-to-face classes, meetings, and workshops that constitute the entire support program. The VLC consists of several elements designed for all cohorts to learn more about inquiry-based teaching of mathematics and science. Some of these elements are open discussion boards, discussion boards limited to specific cohorts, chatrooms, meeting areas, bulletin boards, education databases, libraries, email, and a video portal for showing vignettes from actual classrooms that are exemplars of best practices of teaching.

Originally, districts with which the university had a relationship were solicited to participate in the VLC. Since all first-year teachers in New Jersey are assigned a mentor teacher working in the same school, the VLC provides a forum for mentors to collaborate with their mentees, as well as for mentors to communicate with each other. Other teachers and administrators in the designated districts participate, and university faculty members are available as a resource. PSTs join the VLC during enrollment in mathematics and science methods courses and continue to participate with their cooperating teachers during student teaching. During the mathematics methods course PSTs join the VLC with a password to provide access to the video portal, which includes the MathStore support feature.

In the creation of MathStore, a team of university faculty members and administrators and school district administrators jointly selected local teachers to invite to be videotaped during their regular classroom teaching of mathematics and science. Teachers who were enthusiastic about the project and had demonstrated exemplary teaching (e.g., classrooms with a positive atmosphere, inquiry-based instruction) provided videotapes for analysis. The video selections in this study represent approximately 6 hours of videotapes from a second-grade classroom. After several viewings of the unedited classroom instruction, two mathematics education faculty members independently selected video clips that could be used to illustrate best practices of the teaching of mathematics.

Although there are many elements and issues relevant to the teaching of mathematics, this project focused upon the development of understanding of affect, mathematical representations, mathematical communication/discourse, and engagement. To support this focus, the lead faculty member organized the clips around three themes or strands, which relate directly to key elements of teaching mathematics as prescribed by NCTM:

• Task Design
• Facilitating Students’ Discourse and Supporting Students’ Thinking
• Representations

The video clips were organized into a sequential series of excerpts that could be viewed while simultaneously seeing narratives or commentary. The narratives or commentary were designed to support the viewer’s attention to specific significant elements of the clip and provided clarification of what was being observed. Final narratives and comments were then created to accompany the clips. (See Table 1.)

Table 1.
Sample of the Organization of a Video Clip for Analysis of Strand II: Facilitating Students’ Discourse and Supporting Students’ Thinking.

T

A design team compiled all of the elements of the project. In addition to clarifying and directing narrative, artifacts related to the classroom activity, including actual children’s work, were also made available for viewing within the portal. (See Figure 1.)

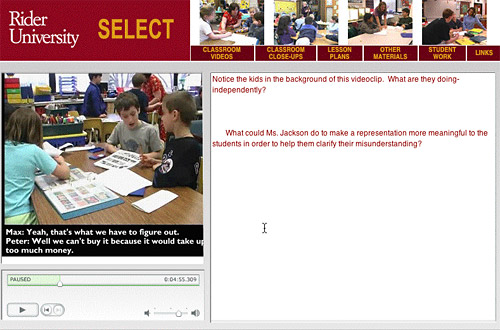
Figure 1. Sample frame from the video portal of the Virtual Learning Community.

Task: Design and Execution

In the vignettes found in the mathematics video portal, children were doing a mathematics problem. The children were told that they had been hired to purchase items from catalogs in order to stock a store with inventory. To begin the task, each child in the class received a personalized letter from The Ultimate Classroom Store, hiring them for this job. They were given some constraints such as having $40 to spend for inventory of a variety of items (at least 200) chosen to satisfy various customer preferences. The children were also asked to include a dozen of any one particular item with a cost between 37¢ and 55¢ each.

The PSTs were given the opportunity to view the video vignettes from this second-grade class. In class, they were provided with laptop computers as they worked in groups of three or four to examine the vignettes, reflect upon their observations, discuss what they observed, and ultimately answer four questions. Within the video portal, the PSTs also analyzed such artifacts as the children’s work and class worksheets. The 10 groups of PSTs each submitted one final written product, which provided data for this study to assess their understanding of the targeted issues. All PSTs watched all of the clips and were able to move back and forth between clips as needed. The assessment questions were embedded in the software to facilitate access at any time.

The four assessment questions assigned to the PSTs were

• Having seen the video clips, do you think that the children really believed they would be hired for this job? At what point does it become an intellectual exercise?
• What kinds of representations did students use to solve problems?
• What is the nature of the conversation among and between children?
• What is it about this task that makes it so engaging?

Results and Discussion

In the following discussion, the preservice teachers will be referred to as PSTs, and the children in the second grade-classroom video clips will be referred to as children except when a part of quotes.

Affect: Reality or Intellectual Exercise?

The first question in the assessment was designed to help PSTs probe the affect of the children they viewed. All of the PSTs agreed that at first the children believed that they had actually been hired to replenish the inventory of the store. The supports and the first question of the assessment guided them to seek the evolution of the problem-solving experience into an intellectual exercise. The PSTs were able to identify significant points in time when the children began to engage in the task as an intellectual exercise. (The group numbers in the following quotations were assigned arbitrarily but are consistent for each group throughout this paper.)

Group 4:	Having seen the video clip, we believe that the children truly believe that they have been hired for this job. The letter to the class along with the delivery made the situation even more realistic. It becomes an intellectual exercise when both the teacher and the students begin defining the problem. Also, the students are assigned specific tasks. The students break up into groups and must really think about the best deals, how to spend their money, and how many items [to purchase].
Group 5:	Yes. There were children jumping up and down saying, ‘We have a job! This is real guys!’ It becomes an intellectual exercise when the children have to start thinking about the problem and the solution to the problem. They understand the boundaries they have and are brainstorming solutions to come up with answers to the questions. It is a process. They have to define the problem, know what information they have, know what information they need to implement a solution.
Group 8:	Having seen the video clip, we thought that the kids really believed they would be hired for this job. They were extremely surprised when the box arrived and excited when they discovered that individual letters were addressed to each student. Because they believed that they were given this responsibility, they were highly motivated to complete the task. The task became an intellectual exercise when the students were presented with the actual letter and the guidelines that needed to be met to complete the task. When the teacher asked what the letter was about, the students began to think intellectually and she continued to prompt them to understand the specific task. She continued to ask questions about what the job entailed, therefore the students would explain what they had to do in their own words. The task became an intellectual exercise at this point and continued as the students began to work in groups and use manipulatives to find a solution.

The PSTs were able to identify points in the timeline of the activity at which the children moved from believing the task involved a real job to one of solving a mathematical problem. Being able to monitor this change is a significant factor in the PSTs’ determination of the children’s affect, which Dai and Sternberg (2004, as cited in Goldin, 2007) regard to be significant in the development of conceptual understanding. Being able to identify this trajectory of activity also is significant because successful performance relates directly to self-perceptions (Hannula & Malmivuori, 1996; House, 2000).

Representations

Although representations had been studied throughout the semester, answering the question about representations used by the children required that the PSTs apply what they had learned as they looked for the use of representations in an actual classroom setting. Most of the groups focused on the use of manipulative materials the children used to represent different aspects of the problem. However some groups recognized the use of pictorial representations, as well.

Group 7:

Students used a variety of representations to solve the problem. They used the catalog to find the items and each price of the items by gross and by dozen… Students also used a chart to represent themselves and what each person was interested in buying.

Group 10:

In Frame 5 of the video we see an example of a type of representation that the students used to solve this problem. We see 3 students discuss within their group the idea that the cost specified in the catalog was for the entire group of items instead of for an individual item. To buy for the store they need to determine the cost for individual items in order to decide if it would be a smart investment.

Whereas most of the PST groups focused on the use of the variety of manipulative materials, some responses indicate that the groups could not only be directed to observe the use of representations, but also to understand the purposes those representations served as aids in solving the problem.

Group 2:	The students use manipulatives as their representation. The manipulatives used in the beginning are cubes and play money. The children use the manipulatives so they can visually see the numbers. With the cubes/money the children were using the strategy of regrouping, trading ten ones for one ten.
Group 3:	The children used manipulatives of their choice to solve the problems. They used the manipulatives to break apart the numbers into equal groups representing a form of division. They used interlocking cubes in frame 12 to find the solution for a single item when items are represented in dozens. They also used digi blocks in frames 16 and 17 independently. Some groups used surveys to keep a tally of which items were more popular.
Group 7:	Students also used the cubes to represent the items that they are going to order. They also used the cubes to divide up the dozen to see how much each one costs per item….Students also used digi-blocks to represent cost of the items and how much money they spent thus far.

The PSTs were directed to observe how the use of manipulative materials represented different aspects of the mathematical solution. Understanding the representations that another person creates is an essential aspect of teaching mathematics. It helps teachers unearth children’s modes of thinking and thereby elicit deeper understanding or redirect misconceptions (NCTM, 2000). Although it is impossible for any of us to observe children’s internal representations, Goldin and Shteingold (2001) indicated that we can ask questions, engaging children in a discourse that will cause them to reveal their thinking. By helping children reveal how their external representations are models for their internal representations, we can attempt to dispel misconceptions. Children do not make changes to their internal models through passive transmission, but instead need active, structured experiences (Schorr & Lesh, 2003).

Discourse

The goal of the third question was to focus on the PSTs’ understanding of what constitutes substantive discourse. Group responses follow:

Group 1:	The nature of conversation between students is one of a learning community. They are stimulating each [sic] others thinking and are comming [sic] to an agreement with each other on how to tackle their problem. When they are discussing with the teacher they are explaining, clarifying, elaborating, and justifying their answers and conclusions.
Group 4:	The nature of the conversation among the children was constructive. The children were in control of how to figure out the problem. They listened to one another and gave feedback to what they felt the best deal was. They explained their answers in order for their peers to understand them. They fed off of each other in order to come up with the best solutions. Children were figuring out for themselves right and wrong answers.
Group 5:	They were discussing solutions and they listened as others gave their solutions. At times the conversation led to arguments but they never went off task. Even unsupervised the students stayed on task.
Group 7:	The nature of the conversation was mixed. At points throughout the video, students are engaged in each other’s conversation. They were interested in what they had to say on what there [sic] ideas were. Working in small groups allowed the students to share their thoughts and ideas with each other. Once the students became extremely involved, they began to become immersed in their own ideas and disregarding some of the other’s ideas. Through the activity, the students stayed focused on the mathematical concepts of the activity.
Group 8:	“We would describe this classroom as child-centered rather than teacher-centered. She didn’t script the lesson. Instead, she would encourage the students to listen to their peers and how they were thinking about the problem. In one group, she did help prompt the student to explain her method of using manipulatives to group. In most groups, one student took charge. The majority of the students continued to work independently with each other and to discuss what they were thinking while the teacher was away from the group.”

The PSTs recognized that it was necessary to examine the discourse when the teacher was present, as well as when the teacher was not present, to get a complete understanding of how these children were communicating mathematically. In the following response, the group was able to tie together various elements of what they observed.

Group 9:

The nature of conversation between students is open and they are all listening to each other and taking turns speaking. Being in this group setting allows for peer teaching as well as independent learning. Students benefit from this environment because they are exposed to a number of solutions allowing them to recognize that there are multiple solutions to one problem. They are able to use manipulatives to help them explain ideas and concepts that are otherwise abstract.

Communication is a noteworthy element in the teaching and learning of mathematics, and one significant aspect of communication is discourse (NCTM, 2000). Teachers need to develop the ability to redirect the discourse when necessary and, in order to do so, must have a clear understanding of what discourse is substantive (Cobb, Boufi, McClain, & Whitenack, 1997).

Engagement

The research on the role of engagement points directly to a correlation between engagement and successful performance (Cabral & Baldino, 2002; Dai & Sternberg, 2004; English, 1997; Goldin, 2000, 2004a, 2004b; Malmivuori, 2004; McLeod, 1992). The intent of the last question of the assessment was to focus attention on what made the task so obviously engaging, in the hope that this would impact task design and selection for future teachers. The PSTs identified a variety of factors that contributed to the obvious engagement of the children in the video.

Group 1:	This task is mostly so engaging to the children because they have ownership of this authentic task. In this problem students are decision makers, they are in charge, it is a child-centered task. They can relate to the problem and they are having fun while doing it. Lastly, the teacher was accepting and did not discourage any students.
Group 5:	It is engaging because they have control over their ideas and solutions. The teacher does not limit their ideas. They are working with items that are interesting to them. They aren’t concentrating on the math but they are concentrating on the task at hand.
Group 6:	The task engages the students because they relate to it as a real-life experience. They feel a sense of responsibility by being assigned such an adult-like task. They are extremely anxious to participate because of the atmosphere in the classroom and the interest in the problem. The problem is not a traditional practice and drill exercise, but rather a hands-on constructivist task. The children will retain the information easier because they were lead [ sic] to their solutions rather than told their solutions. They have increased their schema about shopping and can apply it to the real world.
Group 7:	They are made to feel that their decisions will make an impact on the store. Students are given independence to complete the task using their ideas. This activity is also hands on. Talking, using manipulatives, and conversation all allow students to become engaged.

The members of one group stated explicitly that they were able to make a connection between engagement and progression of the task into an intellectual exercise. Though they did not indicate the role of representations in the engagement, it is implicit in their response to this question. They were able to tie together several facets of the teaching and learning of mathematics.

Group 9:

This answer correlates with question number one because the students feel as though this is a real job, which keeps them intrigued. The children like this activity because it enables them to think freely. There are no limitations set for the way that they go about executing this task. The use of manipulatives kept the children engaged because it enabled them to see abstract ideas more concrete. The fact that they were able to talk to each other about the project also excited the children.

Clearly, the PSTs in that group identified several characteristics of engaging tasks. For future teachers to understand how to create and select mathematical tasks that will be engaging, they must first recognize characteristics of such tasks. The list below represents a compilation of all the characteristics mentioned by the PSTs who were able to identify several criteria of engaging tasks.

• Ownership of the task
• Authenticity
• Students become decision-makers, empowered to make decisions
• Child centered
• Enjoyment
• Encouragement from the teacher
• Related to real life
• Small group settings
• Collaborations
• Solved with the aid of manipulatives
• Students have control over their ideas
• Students have control over their choices

Conclusion and Implications

The 34 PSTs who participated in this study spent nearly a full class period viewing the vignettes, being actively engaged in a discourse of their own, and ultimately responding in writing to the four assessment questions. They were observed referring to the directive and clarifying narratives as they viewed the exemplars, and they stated that these prompts helped to guide their viewing.

Realistically, the process of mastering the teaching of school mathematics, how children learn it, and how to build learning environments in practice, can only begin in courses such as this one. A realistic expectation is that PSTs get a good start in the right direction to support long-term learning on the job. A good start involves gaining a deep, thorough understanding of carefully selected experiences in which important insights can be gained. The right direction, according to the best of current practice, is learning through exploration, inquiry, and discovery as a means of developing rich mathematical concepts and skills.

This research denotes how PSTs honed their understanding of the development of mathematical problem solving in children by changing their own internal models, (Lesh & Doerr, 2003; Schorr & Koellner-Clark, 2003; Schorr & Lesh, 2003) to further promote mathematical understanding that will enhance their practice. The written products of the PSTs in this study reveal that their level of conceptual understanding improved with regards to recognizing the affect of children, understanding the use and applications of various representations, evaluating the discourse among children, and understanding the characteristics of engaging tasks as they all relate to mathematical problem solving.

Those of us who teach methods courses in mathematics for future teachers of elementary school can attest to the fear and phobia that PSTs typically bring to the prospect of teaching mathematics to others. By creating tools that scaffold their understanding of the teaching and learning of mathematics, PSTs may become more empowered to overcome their fears and to become more successful as teachers.

References

Boaler, J., & Humphreys, C. (2005). Connecting mathematical ideas: Middle school video cases to support teaching and learning. Portsmouth, NH: Heinemann.

Bulgar, S. (2002). Through a teacher’s lens: Children’s constructions of division of fractions. (Doctoral dissertation, Rutgers, The State University of New Jersey, 2002). Dissertation Abstracts International, 63/05, 1754.

Cabral, T., & Baldino, R. (2002). Lacanian psychoanalysis and pedagogical transfer: Affect and cognition. In A. D. Cockburn & E. Nardi (Eds.), Proceedings of the 26th annual conference of the International Group for the Psychology of Mathematics: Vol.2. Learning from learners (pp. 169-177). Norwich, UK: School of Education and Professional Development University of East Anglia.

Cobb, P., Boufi, A., McClain, K., & Whitenack, J. (1997). Reflective discourse and collective reflection. Journal for Research in Mathematics Education, 28(3), 258-277.

Cuoco, A. A. & Curcio, F. R. (Eds.). (2001). The roles of representation in school mathematics: 2001 yearbook of the National Council of the Teachers of Mathematics. Reston, VA: National Council of Teachers of Mathematics.

Davis, R. B., Maher, C.A., & Martino, A. M. (1992). Using videotapes to study the construction of mathematical knowledge by individual children working in groups. Journal of Science Education and Technology, 1(3), 177-189.

English, L. (1997). Children’s reasoning processes in classifying and solving computational word problems. In L. English (Ed.), Mathematical reasoning (pp. 191-220). Mahwah,NJ: Lawrence Erlbaum.

Fosnot, C. T., & Dolk, M. (2001). Young mathematicians at work: Constructing multiplication and division. Portsmouth, NH: Heinemann.

Fosnot, C. T., & Dolk, M. (2002). Young mathematicians at work: Constructing fractions decimals, and percents. Portsmouth, NH: Heinemann.

Fraivillig, J., Wish, A., & Bulgar, S. (2004, January). High-tech support for preservice and in-service k-8 teachers of mathematics. Paper presented at the eighth annual conference of the Association of Mathematics Teacher Educators. San Diego, CA.

Goldin, G.A. (2000). Affective pathways and representation in mathematical problem solving. Mathematical thinking and Learning, 2(3), 209-219.

Goldin, G.A. (2004a). Problem solving heuristics, affect, and discrete mathematics. Zentralblatt fur Didaktik der Mathematik International Reviews on Mathematical Education, 36(2), 56-60.

Goldin, G.A. (2004b). Affect in mathematics – exploring theoretical frameworks. In M. Johnsen-Hoines, & A. B Fuglestad,. (Eds.), Proceedings of the 28th annual conference of the International Group for the Psychology of Mathematics: Vol. 1, Inclusion and Diversity (pp. 107-136). Bergen, Norway: Bergen University College.

Goldin, G.A. (2007). Aspects of affect and mathematical modeling processes In R. Lesh, E. Hamilton, & J. Kaput (Eds.), Foundations for the future in mathematics education (pp. 281-296). Hillsdale, NJ: Lawrence Erlbaum.

Goldin, G. & Shteingold, N. (2001). Systems of representation and the development of mathematical concepts. In A .A. Cuoco & F. R. Curcio (Eds.), The Roles of Representation in School Mathematics: 2001 Yearbook. Reston, VA: National Council of Teachers of Mathematics.

Harvard-Smithsonian Center for Astrophysics. (2001). Private universe project in mathematics (Video Series funded by Annenberg/CPB).

Lesh, R., & Doerr, H. (2003). Foundations of a models and modeling perspective on mathematics teaching, learning and problem solving. In R. Lesh & H. Doerr (Eds.), Beyond constructivism: a models and modeling perspective on teaching, learning, and problem solving in mathematics education (pp. 3-33). Hillsdale, NJ: Lawrence Erlbaum.

Malmivuori, M. L. (2004). A dynamic viewpoint: Affect in the functioning of self-system processes. In M. Johnsen-Hoines & A. B. Fuglestad (Eds.), Proceedings of the 28th annual conference of the International Group for the Psychology of Mathematics: Vol. 1, Inclusion and diversity (pp. 114-118). Bergen, Norway: Bergen University College.

McLeod, D. B.(1992). Research on affect in mathematics education: A reconceptualization. In D. Grouws (Ed.). Handbook of research on mathematics teaching and learning (pp. 575-596). New York: Macmillan.

National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.

Olive, J. (2002). Bridging the gap: Using interactive computer tools to build fraction schemes. Teaching Children Mathematics, 8(6), 356-361.

Papert, S. (1980). Mindstorms: Children, computers and powerful ideas. New York: Harper Collins Publishers, Inc.

Powell, A. B., Francisco, J. M., & Maher, C. A. (2003). An analytical model for studying the development of mathematical ideas and reasoning using videotape data. Journal of Mathematical Behavior, 22(4), 405-435.

Schmidt, W. H., McKnight, C. C., & Raizen, S. A. (1996). A splintered vision: An investigation of U.S. science and mathematics education. East Lansing, MI: U.S National Research Center for the Third International Mathematics and Science Study.

Schorr, R.Y., & Koellner-Clark, K. (2003). Using a modeling approach to consider the ways in which teachers consider new ways to teach mathematics. Mathematical Thinking and Learning, 5(2/3), 191-210.

Schorr, R.Y., & Lesh, R. (2003) A models and modeling perspective on classroom-based teacher development. In R. Lesh & H. Doerr (Eds.), Beyond constructivism: A models and modeling perspective on teaching, learning, and problem solving in mathematics education. Hillsdale, NJ: Lawrence Erlbaum.

Tarlow, L.D. (2004). Students’ development of meaningful mathematical proofs for their ideas. In D. McDougall & J.A. Ross (Eds.), Proceedings of the 26th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education: Vol. 2, Building connections between communities (pp. 647-653). Toronto: Ontario Institute for Studies in Education
of the University of Toronto.

Tzur, R. (1999). An integrated study of children’s construction of improper fractions and the teacher’s role in promoting that learning. Journal for Research in Mathematics Education, 30(4), 390-416.

Warner L .B., Davis, G. E., Alcock L. J., & Coppolo, J. (2002). Flexible mathematical thinking and multiple representations in middle school mathematics. Mediterranean Journal for Research in Mathematics Education, 1(2), 37-61.

Warner, L. B., & Schorr, R. Y. (2004). From primitive knowing to formalizing: The role of student-to-student questioning in the development of mathematical understanding. In D. McDougall & J.A. Ross (Eds.), Proceedings of the 26th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education: Vol. 2, Building connections between communities (pp. 429-437). Toronto: Ontario Institute for Studies in Education
of the University of Toronto.

Acknowledgements

This work was supported by Grant Number 02-801020-06 from The New Jersey Department of Education 2002 High-Tech Workforce Excellence Grant for SELECT-VLC: High-Tech Support for a Continuum of Professional Development for Teachers of Science and Mathematics. Any opinions expressed here are solely those of the author and do not necessarily represent the opinions of the New Jersey Department of Education or Rider University.

Author’s Note:

Sylvia Bulgar
Rider University
[email protected]