Computing tasks increasingly make up the majority of STEM (science, technology, engineering, mathematics) jobs, and noncomputing STEM jobs require more knowledge of computing than ever before (Adams, 2020). This is evident in fields such as computational biology, bioinformatics, chemometrics, and computational physics. Recognizing this demand, the Next Generation Science Standards (NGSS; National Research Council, 2013) in the United States included the use of mathematics and computational thinking as two of eight disciplinary practices that are essential for science students to learn.
While computer science (CS) and computational thinking (CT) hold natural places in science classrooms, there is little guidance for teachers about how to integrate CS and CT (Grover & Pea, 2013; Weintrop et al., 2015). While some efforts have been made to prepare secondary science teachers to integrate CT (e.g., Vieyra & Himmelsbach, 2022), most teachers lack the knowledge to meaningfully integrate CT with disciplinary content (Sands et al., 2018). Thus, the integrated scientific and CS skills necessary to get students on a pathway toward computational STEM careers remain elusive .
One promising approach to meaningfully integrating CT in science classrooms is through maker education. Maker education grows out of the broader Maker Movement (Peppler & Bender, 2013), engaging students and teachers in hands-on, project-based learning that combines physical making with computational thinking. Prior research has shown that maker education is successful in engaging students in science, especially students who do not normally feel a sense of belonging in the science classroom (Calabrese Barton & Tan 2018; Tofel-Grehl, 2023). This finding is significant, because early academic preparation predicts students’ career choices (Tai et al., 2006) and the formulation of personal identities compatible with STEM pursuits (Calabrese Barton et. al, 2013; deWitt & Archer, 2015).
This article shares findings from one high school teacher’s efforts to engage physics students in CT within the context of their physics classroom. We report on how physics students engaged CT as an intellectual tool to design, construct, and code escape rooms that leveraged physical science content. Escape rooms, puzzles that participants solve in order to win the game and escape the room, are currently popular with adults and young people alike (Fotaris & Mastoras, 2019). Leveraging this interest, this study explored how to integrate computing into high school physics classes by integrating physics knowledge and computational thinking.
Engaging students directly with STEM content and skills through the design and prototyping inherent to making can provide a meaningful context to further develop STEM identities through interest (Vossoughi & Bevan, 2014). In the study reported here, students utilized low-cost microcontrollers (Micro:bits) and recyclable craft materials to design and build puzzles for their peers to solve (see Figure 1). These puzzles collectively formed a class-wide escape room that students needed to solve to receive a prize.
Figure 1
Example of Student Fabricated Codable ESCAPE Puzzle

The making of these puzzles incorporated elements of embedded computing for controlling the behavior of puzzle artifacts, which showcased various aspects of NGSS-based physics content. In contrast to conventional physical science projects, these artifacts were created using novel materials such as conductive tape or conductive Velcro, sensors for light, sound, and pressure, and actuators such as LEDs and speakers. With these materials, students engaged in designing intellectually rigorous, content-driven, and personally meaningful solutions.
Background
Computing is an essential skill set for many STEM professions. By 2028, the U.S. Bureau of Labor Statistics predicts that three out of four new STEM job openings and three out of five STEM job openings overall will be in computing (Adams, 2020). Increasingly, efforts are underway to engage secondary science teachers in meaningful disciplinary integration of computer science and computational thinking (e.g., Hutchins et al., 2020; Vieyra & Himmelsbach, 2022), but disciplinary integration remains challenging for learners and teachers alike (Basu et al., 2016; Hurley, 2001; Pang & Good, 2000).
Furthermore, despite recent efforts, most teachers are not adequately prepared to effectively guide students in authentic scientific inquiry using traditional classroom tools and practices (Johnson, 2006, 2007). They are even less likely to engage in inquiry using programming, computing, or simulation tools, as they feel less skilled in teaching with these technologies (Belland, 2009; Hargrave & Hsus, 2000). Additional research is needed into how CS and CT concepts should be integrated into science classrooms to establish the necessary foundations for postsecondary and professional pathways toward computational STEM careers (Lee et al., 2020).
Low consensus in the field on the definition of CT further complicates efforts to enhance integration into classrooms. Wing (2006) suggested that everyone should learn to think like a computer by learning how to “[solve] problems, [design] systems, and [understand] human behavior, by drawing on the concepts fundamental to computer science” (p.33). In recent years, several attempts have been made to more precisely define computational thinking (e.g., Barr & Stephenson, 2011; Grover & Pea, 2013; Weintrop et al., 2015). Brennan and Resnick (2012) operationalized CT as sets of key concepts, skills, and practices.
While there are more targeted frameworks for understanding computational thinking in STEM contexts (e.g., Barr & Stephenson, 2011; Weintrop et al., 2015), most of the participants in our study had no prior programming experience. As such, Brennan and Resnick’s (2012) framework for assessing the development of computational thinking in novice learners made the most sense.
The Brennan and Resnick (2012) framework focuses on three dimensions of CT. Computational concepts refer to key programming concepts that appear in many programming languages. These include sequences, loops, events, parallelism, conditionals, operators, and data. Computational practices refer to specific concepts that programmers engage in when building their code, including being incremental and iterative, testing and debugging, reusing and remixing, and abstracting and modularizing. By being incremental and iterative, Brennan and Resnick referred to the ways in which a program is developed, not in one cohesive chunk, but rather through building and testing smaller code segments in increments. As new ideas emerge, the goal for the code might change, requiring the programmer to build and test something new.
Testing and debugging encompasses the practices used to test a piece of code and problem solve when the code does not work as expected. Reusing and remixing describes a common practice in programming of taking and building upon code created by someone else. For novice programmers, this is a way to extend their programming skills beyond where they could go on their own. Finally, abstracting and modularizing is a practice in programming whereby smaller parts are put together to form something much larger.
In addition to computational concepts and practices, Brennan and Resnick (2012) included computational perspectives in their framework. These include expressing, connecting, and questioning. Novice programmers learn that they can use computing to express themselves and to connect with others through what they create. The practices laid out by Brennan and Resnick also map onto several NGSS practices (see Table 1). Through these overlapping practices, connections and integrations can be made to deepen student understanding within and across disciplines.
Table 1
Aligned Standards-Based Practices
| Computational Thinking Practices | Related NGSS Practices |
|---|---|
| Abstracting and Modularizing | Engaging in argument from evidence. Developing and using models. |
| Testing and debugging | Engaging in argument from evidence. Constructing explanations and designing solutions. |
| Being Incremental and Iterative Testing and Debugging | Planning and carrying out investigations. |
Gaming as Context
Escape rooms were selected as a meaningful context for integrating computing into science classrooms, because they are cooperative in nature, impose a time limit, and require problem solving that bridges the traditionally distinct categories of “game” and “puzzle” (Porter et al., 2013). While games are often touted as motivating contexts for learning (e.g., Gee, 2008; Steinkuehler et al., 2012), they are also cultural artifacts that reflect a society’s underlying values and conceptual frameworks (Chick, 1998).
As a medium, puzzling (both solving and designing) aligns well with longstanding calls for more hands-on, project-based science and engineering learning activities in schools (NRC, 2012). Escape rooms, as cooperative problem-solving games that students can both play and create for peers, are optimally positioned to offer both a motivating context for the application of CS/CT and science content and an important opportunity for the linking of school and home cultures through creative STEM engagement. However, most game and puzzle classes take place in out-of-school contexts (e.g., afterschool clubs, summer camps, or libraries), and they are rarely integrated into formal K-12 classrooms. Further, most studies of gaming and puzzling projects are descriptions of a single workshop or isolated class sessions taught by researchers rather than by teachers, limiting the generalizability of the findings (e.g., Halverson & Sheridan, 2014; Hayes & Games, 2008). Accordingly, no models yet exist for the integration of this type of activity into traditional classroom contexts.
Having students design, build, program, debug, and assess their own escape room puzzles not only integrates the computational thinking practices identified by Brennan and Resnick (2012), but also leverages recent enthusiasm for the Maker Movement(Calabrese-Barton & Tan, 2018; Peppler et al., 2016). Specifically, computational making (Rode et al, 2015) refers to making projects that integrate CT alongside attention to aesthetics, creativity, construction processes, and an understanding of the affordances and constraints of various materials.
This study described here explored the affordances of computational puzzle making within high school physics classes to investigate the challenges and affordances of integrating computing into physics. Thus, we posited the following research questions:
- What physical science content do students engage with when tasked with designing and coding puzzles in their science classes?
- What aspects of computing and computational thinking lent themselves to physics class content?
- What challenges and affordances do physics students report valuing when tasked with designing and coding a puzzle that engages science content?
Methods
As part of their classroom work in Advanced Placement (AP) physics, three classes of students used Micro:bits in the making of escape room puzzles. All students were required to keep a reflective journal as part of their homework. These reflective journals captured their responses to teacher prompts about their design process and scientific content application. The teacher, Mr. Kveller (pseudonym), also kept a reflective journal of his experience with the project and was interviewed at the end of instruction.
We conducted a content analysis of these journals, beginning with initial open coding of the texts, followed up with more detailed grouping of codes into cogent findings. The teacher acted as collaborator, clarified interpretation questions when needed, and participated in data analysis.
Participants
The Teacher
Mr. Kveller was in his fifth year of teaching AP physics and was deemed one of the top physics teachers in the state based on student AP test scores. He introduced this project to his AP Physics students after their end-of-the-school-year exam. Mr. Kveller designed, coded, and constructed a number of example escape puzzles for his students to solve. Once students solved these example puzzles, he tasked them with designing a codable puzzle to be solved by other students using the content they had learned during the school year.
The Students
Across three AP Physics classes, 85 students were invited to participate; a total of 50 consented for their journals to be used in this analysis. Demographic information on students was not collected. Advanced placement classes within the K-12 education structure of the United States allow high-performing high school students to take a rigorous class experience that culminates in a nationwide examination that, if passed, accrues college credit. Students in these AP classes had minimal prior physics learning and varied prior coding experience. None of their prior work within the AP Physics class required coding. Most of the students who reported prior coding experience had attended an after-school class or camp.
Context
The School
The school, Lake Woebegone High (LWH; a pseudonym), serves approximately 2,000 students in the suburbs of a metropolitan area in the Western United States. The school is predominantly White, reporting only 15% students from historically underrepresented populations, which is lower than the state average of approximately 26%. Approximately 18% of the school population qualifies for free or reduced lunch, which is lower than the state average of 34%.
Instructional Design Process
In conceptualizing the project and unit for his students, Mr. Kveller engaged a backwards design (Wiggins & McTighe, 2005) approach to building the curriculum and projects. He established his primary learning goals of (a) having students successfully demonstrate adequate physics knowledge to solve the puzzles he designed as models (b) affording students opportunities to design puzzles that demonstrated their physics learning, and (c) student coding of projects that brought together coding and physics as a means of modeling for students learning of both.
While his instructional goals were not tailored to this study, he modeled the skills and strategies students needed as he built his models. Documents explicate the design of each model project used as part of the instructional process. As noted in the methods, the questions asked of students were designed by the teacher in his capacity as instructor to assess their learning in the classroom.
Overview of Teacher Project Activities
Within the context of his AP Physics classes, Mr. Kveller designed, coded, and constructed a series of escape puzzles for his students to solve to “unlock” their classroom and win a prize (see Figure 2). Images and descriptions of each puzzle are provided here to elucidate the richness of science content covered through integrated puzzling and computing. As part of his model escape room, Mr. Kveller made puzzles covering optics, electromagnets, and circuits, demonstrating the varied ways that the sensors built into Micro:bits could be used to model physics phenomena. Once students solved Mr. Kveller’s puzzles, they were allowed to design, code, and build their own puzzles for peers to solve.
Figure 2
Optics Puzzle With Flashlight, Magnifier, and Mirror to Utilize Micro:Bit’s Light Sensor

Overview of Student Project Activities
Leveraging the creative and physical properties of making puzzles, the escape room project focused on two distinct but related areas of classroom learning: integrated STEM (puzzle design) and standards-aligned content. After completing Mr. Kveller’s puzzles, students were put into groups and tasked with designing, coding, and constructing puzzles of their own imagination. During the subsequent class periods, totaling approximately 200 class session minutes, students worked collaboratively to meet the design challenge set by their teacher. Constraints included (a) students needed to use Micro:bits to record or measure some scientific phenomenon discussed during the prior 8 months of AP Physics and (b) the puzzles had to be constructible with materials on hand in the classroom.
Data Collection and Analysis
A mixed methods content analysis was conducted to bring clarity to the nuanced data in student reflection journals. Because little established theory exists exploring the integration of computing, gaming, and physics education, qualitative content analysis of student reflection journals employed the conventional method (Tesch, 1990). As Hsieh and Shannon (2005) noted,
Researchers immerse themselves in the data to allow new insights to emerge (Kondracki & Wellman, 2002), also described as inductive category development (Mayring, 2000).… Data analysis starts with reading all data repeatedly to achieve immersion and obtain a sense of the whole (Tesch, 1990) as one would read a novel. Then, data are read word by word to derive codes (Miles & Huberman, 1994; Morgan, 1993; Morse & Field, 1995) by first highlighting the exact words from the text that appear to capture key thoughts or concepts. Next, the researcher approaches the text by making notes of his or her first impressions, thoughts, and initial analysis. As this process continues, labels for codes emerge that are reflective of more than one key thought. These often come directly from the text and then become the initial coding scheme. Codes then are sorted into categories based on how different codes are related and linked.
Within this analysis, student journals were read holistically and then coded for key words and themes. Iterative review of the data found prominent codes focused on student achievement (e.g., bringing ideas to life) and challenges (e.g., engaging the block coding environment). The data were reviewed for further evidence of the value of these codes or disconfirming evidence that they were not central to student meaning making and experiences. When analyzing the data around students’ selection of specific physics topics for their puzzles, quantifying those occurrences made sense to allow for the distillation of patterns within the data and give weight to the choices made by students. Validity was established by all reviewers coming to consensus on the coding and through extensive member checking with the classroom teacher, who participated as an author in this work.
Data collected during the study included weekly student journal entries, photographs of artifacts, photographs of student code, and teacher reflections. Student responses were coded to capture the descriptive nature of content engagement. An initial analysis of student journals was conducted to broadly quantify student engagement with physics and coding.
We analyzed student journals for frequency of the strands of physics content students engaged for their puzzle to provide an overview of alignment with content standards. We analyzed data thematically to seek an overview of the trends noted in the data focused on affordances of and engagement with computing during physics projects. Secondary analysis was conducted by two researchers to distill discrete trends around student engagement with coding and collaboration.
Findings
RQ 1. Physics Content
Across all student-designed projects, the physics content engaged with included principles of motion and electricity, in addition to the target curricular content emphasized by the participating teacher. Table 2 delineates the physics content topics and frequency with which students used them to construct their puzzles. These included accelerations and freefall, circuits, Newton’s second and third laws of motion, and kinematics. Note that the total percentage of students engaging content topics could exceed 100%, as students might have engaged multiple science content strands through their puzzles.
Table 2
Summary Table of Physics Content Observed Within Student Projects

Students engaged in different topics across the physics content, but encountered several of the same challenges and successes throughout the process of designing, constructing, and coding their escape room puzzles. While individuals’ preferred areas of science differed, commonalities of experience existed across computing and collaboration experience.
RQ 2: Aspects of Computing and CT
Because the parameters of the design task assigned and the available code blocks within the Micro:bit environment constrained student approaches, most of the students’ coding choices appear to be fairly uniform. For example, all student projects used if-then statements and forever loops. In students’ journals, they noted that the use of Micro:bit sensors drove their coding decisions. As one student commented regarding the challenges of using the Micro:bit’s sensors, “I would’ve liked a refresher on how the coding works with the light intensity sensor.… The light sensor took a long time to figure out.”
The table in the appendix delineates the aspects of CT and the specific coding choices students made when tackling specific aspects of physics. Of particular interest was that all projects engaged all aspects of computational concepts identified by Brennan and Resnick (2012), except parallelism (i.e., sequences, loops, events, conditionals, operators, and data). Parallelism was not noted in the code for projects focused on acceleration and free fall and Newton’s Laws.
Many students talked about the procedural and iterative nature of their coding processes and the inherently cyclical way they engaged in coding their projects. Furthermore, students immediately noted how these projects required a great deal of testing and debugging, a key computational practice identified by Brennan and Resnick (2012). As they moved through iterative cycles of testing and debugging, two practices that were deeply intertwined in how students experienced their puzzles, many students noted that they used iterative processes of “trial and error” to achieve success. Students from all projects noted that trial and error was part of their debugging and coding process; for example, “When I didn’t understand what the code said, I used trial and error.” As another student noted,
I found getting the code in the right order the most challenging today. It took a while to understand how the placement of the code can affect the Micro:bit as a whole. But after I figured that out it was pretty simple.
Students also reflected on the value of iteratively debugging and testing their projects and code. As one student noted, “Getting through a lot of the coding and figuring out the little bumps were most of the ‘ah hah’ moments.” Students generally valued debugging as a practice. As another commented, “I have had coding experience, and things rarely work the first time, but we got it to work pretty fast, and it was satisfying.” Students also began to connect their initial coding efforts within the project with their final products, with many noting they could reuse code from earlier in the project. For example, one student, when discussing their challenges with coding, noted that it was hard:
Trying to smooth out all the bumps and getting the coding to do exactly what we wanted and stopping it from looping. [But then] getting two of our three Micro:bits programmed, because now we only have one left to do. We have a plan for the third, so we are past the brainstorming step entirely.
When we examined the code from the group just referenced, we noted that their code was reused from Micro:bit to Micro:bit. Students began to appreciate the ability to reuse and remix earlier code as a mechanism for moving forward in their task. By remixing and reusing code, students were more capable of completing their projects, which was universally reported by students as the most rewarding aspect of their projects.
Most students reused chunks of code across steps of their projects. In reflecting on this and what code allowed them to do, one student noted, “I thought that despite being difficult it was good for me to think in a different way. I feel like I need to work on thinking from another angle, and this allowed me to do that.”
Students recognized the value of examining their physics learning from a new lens. Another student reflected on the abstract nature of coding the Micro:bit to measure acceleration, commenting,
Our puzzle gives the mass of the Micro:bit and the acceleration of the Micro:bit and asks for the mass needed to reach that acceleration. Using the equation F = ma and using the net force of the tension forces, which would be the masses of the Micro:bit and the weights, you would multiply mass and acceleration to get net force. Then you would subtract the mass of the Micro:bit to find the masses needed to solve the puzzle.
Abstraction is observed here in two layers. First, students abstracted from the physical phenomena to the equation and then again from the equation to the representation of it in block code. Both the CT concepts and practices engaged through the puzzle design, construction, and coding influenced student understanding of both computing and physics.
RQ 3. Challenges and Affordances
Broadly speaking, students demonstrated a high level of engagement with both science content and computing in the designing and making of their puzzles. Students reported two sets of challenges in bringing their projects to fruition and two discrete affordances they perceived from engaging computing within their physics class. Students identified learning the coding and needing to temper their physics vision as challenges, while they saw manifesting their vision and bringing their physics learning to life as positive affordances of coding.
Because this was a science class, it was expected that students might come into this project with varied degrees of awareness and ability regarding coding, and this bore out across the classes. Having worked with the class for nearly a full school year, the teacher felt that students across classes had a strong and equal understanding of the physics content.
Challenge 1: Lack of Familiarity With Coding or Coding Environment
Student reflections confirmed that the learning trajectory around coding was the most challenging aspect of the project. As one novice coder responded in their journal, when prompted to reflect on what was challenging, “Just getting over the learning curve of never really having coded before. I’m slowly learning how to use the program so it’s a little difficult for me.”
Another student, one who did have prior coding experience, noted their lack of familiarity with the specific coding environment, commenting that “the coding was difficult because we were used to Scratch, and there were some blocks we could not find.” In this way, prior coding experience was not necessarily helpful to students, as they came in with understandings of coding and expectations of how the coding environment would accommodate their plans that may not have matched the system they were using.
Another student noted that one of their group’s challenges was “getting the coding just right and working through all the bugs.” Students’ expectations about what the coding environment would permit them to do often led to frustration, even when it came to simple misunderstandings about the features and buttons within the block code environment. Student frustration with coding was exemplified through one student’s comment:
The hardest part about the coding is when you cannot find the FLIPPIN triangle button or the circle buttons, and so you’re really confused which ones are the oval ones.… The Micro:bits can be quite sensitive.
Yet another student commented,
The most challenging part of the project was definitely the code (mostly technical difficulties). I didn’t do the coding personally, but my teammates had lots of problems. Our board wasn’t complicated, just doing the actual circuit was that hard.
This student opted out of the coding portion of their project because of the perceived challenge. Going further, one student with a good deal of prior coding experience noted, “I had a hard time working with the Microsoft IDE. The IDE was very opinionated and didn’t offer any flexibility, thus making it really hard to program any code into the Micro:bit.” However, later on the same student noted, “I was able to write up 250+ lines of code and my Micro:bit was able to work. This was rewarding because I was able to complete this within a small amount of time.” This shift from being frustrating to rewarding was observed across groups and projects when discussing coding.
While students were able to make progress toward their goals, students also recognized that they needed better scaffolds to successfully code their projects. As one student noted, “We struggled a little bit with the coding because it was hard, but we figured it out. Maybe a deeper lesson about coding would have helped.” Another student also noted that for the coding aspects of the project, “a guide would have been nice.” Another student actively advocated for more supports, saying “To make coding easier, I would’ve liked a refresher on how the coding works with the light intensity sensor.”
These students, while not using the term itself, sought scaffolds and opportunities for practiced worked examples to support their learning and application of coding to their physics class. These types of reflections were common across veteran and novice coders alike, with several students commenting that at times their process for figuring out the Micro:bit coding environment was “trial and error.”
Challenge 2: Tempering Vision With Ability
Students also reported difficulties in getting the code to work with their puzzle vision and construction designs. For many, there was often a disconnect between their vision and their coding ability, both for novice and more experienced coders alike. As one student noted, their group was challenged by “deciding on a specific design, because we had a lot of ideas and none of them were easy to implement.” Another student commented, “I was part of the coding [team], so I found out what we had decided on for our project for the coding was too difficult to do.” Another student noted,
I found the hardest part of designing and building today was trying to figure out what worked. What we began with was a little bit too complicated, and we figured out how to make it simple for us and simple for the solver to figure out the concept.… I was so happy when we figured out how to make it cohesive and got the Micro:bits to work together.
These realizations caused some groups to opt to change their project design, as noted in students’ journals with comments such as, “We decided to change the coding to something simpler.… What we decided for our project, well, the coding for it was too difficult to do.” This iterative change process was bidirectional for some groups with one student noting, “when we messed up on some coding and had to go back and fix it to make the physics applicable.”
For many groups there were multidirectional processes of debugging, so they needed to resolve coding and construction issues simultaneously, which proved challenging. As one student explained regarding their acceleration project,
The construction of our ramp for our puzzle and the coding for the Micro:bit was very challenging, because it wouldn’t work sometimes and we had to problem solve many times…. Although we were able to make the Micro:bits find acceleration, it was a very long process, and took a lot of trial and error.
For some groups, trial and error was not sufficient to overcome a paucity of computing knowledge. For some student groups, this meant figuring out how to code something that they did not immediately know how to do. Others opted to rework their constructed physics designs to allow for simpler code. For example, one group opted to use more Micro:bits so that they could have each Micro:bit doing a different task, rather than trying to figure out how to code one to execute multiple steps. This involved rebuilding their entire game board, but they felt that this modification was more efficient than engaging more complex coding. This created a multidirectional space in which to engage goals either through modification of the physical object constructed or the computing engaged.
While most students felt that the code was the most challenging aspect of the project, many also felt that it was the most rewarding, as it allowed them to take their ideas from concept to physical artifact as well as provided them with a meaningful grounding and application of their physics knowledge. Specifically, two affordances were noted: their ability to manifest their vision of the puzzle from concept to physical object that they were able to code to do what they wanted and bringing their physics learning to life.
Affordance 1: Joy at Manifested Vision
By coding their projects, students felt there was a sense of permanence and purpose to their work. As one student noted, “Seeing the completed project work was pretty great, knowing we helped make it work.” For all groups, the ability to design, code, and construct a working project was the most valuable aspect of the work.
After engaging in these processes, youth felt their greatest reward was seeing other folks struggle to solve their puzzles. Students felt that the struggle of others indicated a worthy and challenging puzzle. One student noted, “The most rewarding aspect of the project was seeing the other teams solve it. It was good to see it work for other people and not just for us, who knew how to solve it from the beginning.” Another group noted, “It was the most rewarding to see something on paper come to life! We worked hard to form an idea but carrying it out meant so much more!” As one group member commented, “It was rewarding to see when our code worked, and we could hear the music because we accomplished something a lot of kids couldn’t do.” Notions of artifact permanence and bringing their ideas to fruition were reported by nearly all students. Coding allowed students to make something more tangible and actionable than their standard physics work, which resulted in students having a heightened sense of satisfaction and reward from their science learning.
Furthermore, across groups, students reported feeling a sense of accomplishment when code worked correctly. This sentiment is well summarized by a student who wrote, “I was so happy when the programming finally worked like we wanted it to!” Students articulated a desire to learn more and become more proficient coders. Several students said that stronger coding skills would afford them the ability to make richer and more complex projects in the future.
As one student noted, his primary frustration was “that the code did not do what we wanted it to do at first” and “coding better would make it faster and more fun.” Yet another student noted,
Finding out how to code the Micro:bit in order to measure the acceleration and give a win condition [was challenging]. It was difficult to find how to have the Micro:bit display the win condition if the answer was correct and the opposite for an incorrect answer.
These reflections indicate how important manifesting their group’s puzzle vision was to students. Coding was essential to this sense of manifested vision because, as one student noted, “The most rewarding part of coding was seeing the end result.” Another student felt a profound sense of accomplishment when she succeeded at coding her project, noting, “When you finish the coding, it’s really satisfying as you can see and feel completed in life and you feel like you’ve done such an amazing job and you feel amazing inside.” As another student stated, “Having the display work was the most rewarding, because it’s physical evidence that what we did works.” Another student confirmed this sentiment when they noted, “It was very rewarding to see the code work with the puzzle and see an idea be made into a working puzzle.”
While coding presented a universal challenge, it was also something that led to great persistence from students specifically because coding was the tool that allowed them to bring an idea from the abstract into the concrete. This persistence appeared to stem from an interaction between student valuing of the permanence of their idea as represented in the puzzle and their ability to program that object (Figure 3).
Figure 3
Coding Micro:bit to Provide Clues
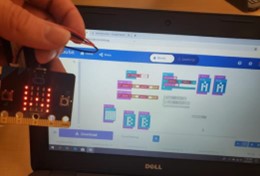
Students reported a sense of pride in their efforts to design a viable and solvable puzzle as well as a sense of satisfaction from other students solving their puzzles. As one group of students commented, “It was the most rewarding to see something on paper come to life! We worked hard to form an idea but carrying it out meant so much more!” Reporting on their group’s activities, another student wrote,
Solving other puzzles and seeing what people came up with because it is super interesting to see how other people think. It was also satisfying to have something real to do with the physics knowledge I know I have.… To see our puzzle work correctly and be able to solve others puzzles.… I think watching other groups struggle and then for them to solve it, because they would turn and look and tell us how great it was.
Students commented that these projects and ideas transcended the single classroom experience because students were able to generate new ideas and objects that survived. Frequently students discussed “seeing the idea come to life.” When thinking about the code, students were excited to create something that could be applied to new puzzles and projects. As noted by one student, “I was able to create an abstract program that we can use for further development.” For students in these physics classrooms, coding and constructing puzzles represented an opportunity for durability of their work and thinking that they had not experienced in other science class learning.
Students reported high levels of intellectual satisfaction in being able to take an idea from concept to functional object. They reported high engagement with others that both motivated and challenged them. As one student noted, “Having the display work was the most rewarding because it’s physical evidence that what we did works.” Bringing an idea to life was meaningful to students as evidenced by one student stating, “It was satisfying to see the finished product.” Student ownership of the learning and product is made evident in this statement from another student who said, “I found that building something with my hands and being able to see something develop due to my own work and that of my teammates was especially rewarding.”
Affordance 2: Grounding of Physics
A second affordance of computing in physics class was a direct impact on students’ perceptions of their own physics knowledge. Students reported that designing and building codable puzzles gave deeper meaning to their physics learning, as one group member commented when asked what was most rewarding about the work:
Solving other puzzles and seeing what people came up with, because it is super interesting to see how other people think. It was also really satisfying to have something realistic to do with the physics knowledge I know I have.
Being able to engage their knowledge of physics with the Micro:bits was compelling to students. Many students commented that the sensors built into the microprocessors were essential and meaningful parts of their content integration as they designed their puzzles. While different groups used different component parts of the Micro:bit, they were each used as tools in capturing and demonstrating the targeted scientific phenomena. Students expressed satisfaction and success at figuring out how to do this. Students, for example, noted the following:
We were able to code the Micro:bits to do find acceleration, which is very complex. We eventually figured out how the light sensor worked on our Micro:bit.
I was able to get the motion sensor built in the micro-bit [sic] to display simple string values. I also found that I can create my own functions for further use and pass in my own arguments into said functions.
When engaging with the physics content they were attempting to model in their puzzles, students expressed frustration and challenges in coding the Micro:bits to properly model the physics content. Students quickly realized that the specificity of the Micro:bits did not account for human error. For example, multiple students noted that getting Micro:bits to compute acceleration was difficult because of variation in how and when individuals released the object while completing the puzzle. As one student commented in his journal, “Although we were able to make the Micro:bits find acceleration, it was a very long process and took a lot of trial and error.” Yet another student reported,
An a-ha moment that we had when designing the puzzle occurred while we were coding. When we came across certain problems while coding, we remembered certain components that could make it not work, such as friction. Through that, we were able to solve the problem by making friction negligible.
Students found that getting the Micro:bits to account for the human element to make the puzzles solvable was difficult for them. However, with practice and use students noted, “I think the more we use MakeCode, the easier it becomes.” For these students, the science content understanding was strong, while the CS/CT knowledge necessary to code their puzzle was less robust. However, despite the challenge, the students persisted at engaging with the science content and coding the sensors to make functional escape room puzzles.
Discussion
Integrating computing and science can create many challenges for teachers and students. Teachers are not prepared to engage computing within their core content classes and standardized testing drives teachers to focus on their core content. However, their integration creates significant opportunity for rich learning of core content through the engagement of computing as a tool for improved modeling and exploration of scientific phenomena. Within our study, students were able to access and model a wide range of physics content, including kinematics, Newton’s laws, and acceleration, through the construction and coding of their projects. Through the process of coding their projects, students were able to think deeply about their physics content and use the coded Micro:bits as models for measuring and engaging the physical science phenomena they studied in physics class.
Given the value to students, assisting teachers through professional development, preservice training, and curricular scaffolds could better facilitate the integration of computing and physics at the classroom level. Without such scaffolds and supports, teachers are less likely to attempt such integrations on their own.
Furthermore, making appears to add an additional layer of nuanced opportunity for students. Our findings indicate that students see value in having work that transcends the classroom daily experience. Typically, in science classes, labs and projects are deconstructed at the end of each class period to be reset for the next group of students. Students invest time and energy into constructing or completing something that is deconstructed and reset for the next group who enters the classroom. However, in our project, students engaged in making projects that survived the class period. They were permanent and other students were allowed to engage with them.
Coding added a level of permanence and meaning to student work because the code created existed beyond a specific project or student, as noted in student comments about the value of bringing their ideas to fruition. Given the value students articulated around the permanence of the artifact and code, supporting teachers in developing ways for students to experience a more lasting sense of impact from their inquiry is needed. In doing this, professional development providers and curriculum designers can leverage the cheap material costs of making toward more deeply valued projects for students.
Implications
Often in science classrooms, laboratories or demonstration have a transactional nature, with student work passing from sight before they even leave the classroom. Often students spend a class period working on an experiment or lab project, only to have their efforts disassembled in order to prepare the materials for the next class of students. Similarly, students in traditional CS classes complete screen-based exercises that do not have a meaningful life beyond the screen and outside the context of the class.
In this study, students saw value in coding projects that were afforded the meaning and respect of retaining their existence. Understanding the ways in which students can engage computing in their core content classes is essential for developing more equitable computer science education. Furthermore, broadening what educators define as CS and who can do it can further engage groups needed in CS.
Our findings indicate several things that warrant further examination and consideration by teacher educators. While our examination occurred in physics, it should not be limited to that context solely. As is the case with physics, computational inquiry activities have significant potential for transforming any area of science education. Whether using simulations or building low-cost models through traditional maker activities, all areas of science would benefit from affording students the opportunity to use computing and computational thinking skills within the science classroom.
With students telling us that bringing their ideas to life matters to them, we should explore the ways in which computing affords young makers and students of science even greater opportunities to do this. Doing so furthers the NGSS goal that school science look more like professional practice in science. With tools such as BBC Micro:bits, science sensors and tools can be readily available to students. While, historically, students have only been afforded the chance to read and observe changes in these phenomena, now with microprocessor sensors, students can model outcomes based on computerized readings. This takes the student from passive observer to engaged actor. Modeling outcomes also creates a potentially transformative shift in the role of science student and one that is afforded only to students with sufficient mastery of code to program such sensors.
Ethics and Statement
All research reported herein was conducted in keeping with the guidelines and ethics set forth by the Utah State University Institutional Review Board. Participants were consented following procedures laid out during the process approved by USU’s IRB.
Acknowledgements
This work is the culmination of a semester long exploration of ways to engage physics students in using computing for physics learning. The authors wish to acknowledge the students who graciously contributed to our understanding of what is possible.
References
Adams, J. C. (2020, May). Retrospective: A look back at 20+ years of experience in parallel computing education. In Proceedings of 2020 IEEE International Parallel and Distributed Processing Symposium Workshops (pp. 252-260). https://doi.org/10.1109/IPDPSW50202.2020.00056
Barr, V., & Stephenson, C. (2011). Bringing computational thinking to K-12: What is involved and what is the role of the computer science education community? ACM Inroads, 2(1), 48-54.
Barron, A. E., Kemker, K., Harmes, C., & Kalaydjian, K. (2003). Large-scale research study on technology in K-12 schools. Journal of Research on Technology in Education, 35, 489-507.
Basu, S., Biswas, G., Sengupta, P., Dickes, A., Kinnebrew, J. S., & Clark, D. (2016). Identifying middle school students’ challenges in computational thinking-based science learning. Research and Practice in Technology Enhanced Learning, 11(1), 1–35.
Belland, B. (2009). Using the theory of habitus to move beyond the study of barriers to technology integration. Computers & Education, 52, 353-364.
Calabrese Barton, A., Kang, H., & Tan, E. (2013). Crafting a future in science: Tracing middle school girls’ identity work over time and space. American Educational Research Journal, 50, 37-75.
Calabrese Barton, A., & Tan, E. (2018). A longitudinal study of equity-oriented STEM-rich making among youth from historically marginalized communities. American Education Research Journal, 55(4). doi: 10.3102/0002831218758668
Chick, Garry. 1998. Games in culture revisited: a replication and extension of Roberts, Arth, and Bush (1959). Cross-Cultural Research, 32(2),185–206.
deWitt, J., & Archer, L. (2015). Who aspires to a science career? A comparison of survey responses from primary and secondary school students. International Journal of Science Education, 37(13), 2170-2192.
Fotaris, P., & Mastoras, T. (2019, October). Escape rooms for learning: A systematic review. In L. Elbaek, G. Majgaard, A. Valente, & S. Khalid (Eds.), Proceedings of the European 13th International Conference on Games Based Learning (pp. 235-243). Academic Conferences and Publishing International Limited.
Gee, J. P. (2008). Learning and games. In K. Salen (Ed.), The ecology of games: Connecting youth, games, and learning. The MIT Press.
Grover, S., & Pea, R. (2013). Computational thinking in K-12: A review of the state of the field. Educational Researcher, 42(1), 38-43. https://doi.org.dist.lib.usu.edu/10.3102/0013189X12463051
Halverson, E. R., & Sheridan, K. (2014). The maker movement in education. Harvard Educational Review, 84(4), 495-504.
Hayes, E. R., & Games, I. A. (2008). Making computer games and design thinking: A review of current software and strategies. Games and Culture, 3(3-4), 309-332.
Hargrave, C. P., & Hsus, Y. (2000). Survey of instructional technology courses for preservice teachers. Journal of Technology and Teacher Education, 8, 303- 314.
Hsieh, H. F., & Shannon, S. E. (2005). Three approaches to qualitative content analysis. Qualitative Health Research, 15(9), 1277-1288.
Hurley, M. H. (2001). Reviewing integrated science and mathematics: The search for evidence and definitions from new perspectives. School Science and Mathematics, 101(5), 259–268.
Hutchins, N.M., Biswas, G., Maroti, M., Ledeczi, A., Grover, S., Wolf, R., Blair, K.P., Chin, D., Conlin, L., Basu, S., & McElhaney, K. (2020). C2STEM: A system for synergistic learning of physics and computational thinking. Journal of Science Education and Technology, 29, 83-100. https://doi-org.dist.lib.usu.edu/10.1007/s10956-019-09804-9
Johnson, C. C. (2006). Effective professional development and change in practice: Barriers science teachers encounter and implications for reform. School Science and Mathematics, 106, 150-161.
Johnson C. C. (2007). Whole-school collaborative sustained professional development and science teacher changes: Signs of progress. Journal of Science Teacher Education, 18, 629–661.
Lee, I. Grover, S., Martine, F., Pillai, S., Malyn-Smith, J. (2020). Computational thinking from a disciplinary perspective: Integrating computational thinking in K-12 science, technology, engineering and mathematics education. Journal of Science Education and Technology, 29, 1-8.
Lui, D., Kafai, Y.B., Walker, J.T., Hanna, S., Hogan, K., & Telhan, O. (2019). A reevaluation of how we think about making: Examining assembly practices and artifact imagination in biomaking. In P. Blikstein & N. Holbert (Eds.), LF2019: Proceedings of FabLearn 2019 (pp. 34-41). ACM.
Peppler, K., & Bender, S. (2013). Maker movement spreads innovation one project at a time. Phi Delta Kappan, 95(3), 22-27.
Peppler, K., Halverson, E., & Kafai, Y. B. (2016). Makeology: Makerspaces a learning environments (Vol. 1). Routledge.
Porter, L., Guzdial, M., McDowell, C., & Simon, B. (2013). Success in introductory programming: What works? Communications of the ACM, 56(8), 34-36.
National Research Council. (2012). A framework for K-12 science education Practices, crosscutting concepts, and core ideas. National Academies Press.
National Research Council. (2013). Next generation science standards: For states, by states. www.nextgenscience.org/practices/using-mathematics-and-computational-thinking
Pang, J., & Good, R. (2000). A review of the integration of science and mathematics: Implications for further research. School Science and Mathematics, 100(2), 73-82.
Ramey, K.E., & Stevens, R. (2019). Interest development and learning in choice-based, in-school making activities: The case of a 3D printer. Learning, Culture and Social Interaction, 23. https://doi.org/10.1016/j.lcsi.2018.11.009
Rode, J. A., Weibert, A., Marshall, A., Aal, K., von Rekowski, T., El Mimouni, H., & Booker, J. (2015, September). From computational thinking to computational making. In K. Mase, M. Langheinrich, & D. Gatica-Perez (Eds.), Proceedings of the 2015 ACM International Joint Conference on Pervasive and Ubiquitous Computing (pp. 239-250). ACM.
Sands, P., Yadav, A., & Good, J. (2018). Computational thinking in K-12: In-service teacher perceptions of computational thinking. In M. S. Kine (Ed.), Computational thinking in the STEM disciplines (pp. 151-164). Springer, Cham.
Steinkuehler, C., Squire, K., & Barab, S. (Eds.). (2012). Games, learning, and society: Learning and meaning in the digital age. Cambridge University Press
Tai, R. H., Liu, C. Q., Maltese, A. V., & Fan, X. (2006). Planning early for careers. Science, 312, 1143-1144.
Tesch, R. (1990). Qualitative research: Analysis types and software tools. Falmer.
Tofel-Grehl, C. (2023). If science doesn’t care about me why should I care about it?: An Indigenous Hawaiian student’s experience of community science in building science belonging. Journal of Research in Science Teaching. VOL/ISSUE/PG #S?
Vieyra, R., & Himmelsbach, J. (2022). Teachers’ disciplinary boundedness in the implementation of integrated computational modeling in physics. Journal of Science Education and Technology. 31, 153-165. https://doi-org.dist.lib.usu.edu/10.1007/s10956-021-09938-9
Vossoughi, S., & Bevan, B. (2014). Making and tinkering: A review of the literature. Commissioned paper by the Committee on Successful Out-of-School STEM Learning.
Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Truille, L., & Wilensky, U. (2015). Defining computational thinking for mathematics and science classrooms. Journal of Science Education and Technology, 25, 127-147.
Wiggins, G., & McTighe, J. (2005). Understanding by design. ASCD
Wing, J. M. (2006). Computational thinking. Communications of the ACM, 49(3), 33-35.
Appendix
Summary Table of Computing Tasks Observed Within Student Projects
![]()