Effective mathematics instruction calls for teachers to enact teaching practices and utilize tools that promote student sensemaking. Technology as an educational tool has shown continued presence and promise in elementary classrooms (Cheung & Slavin, 2013), and research has focused on exploring and describing the integration of effective mathematics teaching (National Council of Teachers of Mathematics [NCTM], 2014) and technology use (Estapa & Nadolny, 2015; Gould & Schmidt, 2010). Results of this work illustrate how technology can foster student engagement in mathematics and encourage mathematical risk taking (Palaigeorgiou & Papadopoulou, 2018).
Technology has also been utilized in the mathematics classroom for self-regulated learning (SRL), where students’ technology experience is more independent and paced to match their understanding. Research has shown SRL to support students’ learning and achievement in all core academic-domains (Zimmerman & Schunk, 2011), including mathematics (Callan & Cleary, 2018). Across all domains, teachers play a key role in understanding the interplay between the content being taught, the pedagogical approaches being used, and the technology being integrated (Mishra & Kohler, 2006).
Within our study, we analyzed the experiences of teachers during a classroom based SRL experience. In this case, teachers used a combination of self-paced, online instruction and teacher-paced, face-to-face instruction, a scenario which falls under the category of SRL. The purpose of this study was to examine and better understand teacher experiences during the implementation of a self-regulated online mathematics program in their classroom. More specifically, we investigated the teachers’ experiences and actions in terms of questioning strategies and responsive pedagogy in the SRL mathematics learning environment.
Understanding how teachers promote student sense-making during the enactment of self-regulated online mathematics programming provides guidance for effective practices while supporting the implementation of face-to-face and online learning to assure elementary students experience responsive interactions that optimize their learning. It is critical the educators understand details of SRL, as more online learning environments have been utilized due to the global COVID-19 pandemic. Further, understanding pedagogical aspects of SRL will benefit teacher education programs as they work to prepare future teachers to implement effective teaching approaches where online and face-to-face instruction complement each other.
Responsive Teaching
To analyze responsive interactions within an SRL experience, we grounded our research design and analysis in responsive teaching concepts. Richards and Robertson (2015) highlighted three processes of responsive teaching as when teachers (a) foreground attention to the substance of students’ thinking, (b) recognize disciplinary connections within those ideas, and (c) take up and pursue students’ ideas (p. 36). In this way, “a responsive approach builds from the view that children are richly endowed with resources for understanding and learning” (Hammer et al., 2012, p. 55). As such, the construct of responsive teaching allows researchers to analyze not only when teachers take up student thinking but also the decisions around such actions.
Research highlights that when teachers take up students’ ideas they empower and deepen student learning and increase student performance (Carpenter et al., 2000; Jacobs et al., 2010). Lineback (2015) conveyed the importance of this work, stating, “The educational research community stands to benefit from the continued exploration into how, when, where, and to what end teachers attend and respond to students’ thinking” (p. 225). Teacher questioning is an effective pedagogical strategy to elicit student thinking. Once student thinking has been elicited, a teacher makes a decision to take up student thinking or not. Fitzgerald and Palincsar (2019) reported that teacher questioning is the most frequent practice associated with supporting student sensemaking. Therefore, through a responsive teaching lens we sought to answer the following research question: How does teacher questioning support responsive teaching in an SRL environment?
Literature Review
This literature review provides the background for self-regulated learning as it informs our research and design. Self-regulated learning is presented within the context of effective teaching and teacher responsiveness while situated in mathematics instruction. The first section of this literature review provides our working definition of self-regulated learning.
Self-Regulated Learning
Panadero’s (2017) definition of self-regulated learning is “a core conceptual framework to understand the cognitive, motivational, and emotional aspects of learning” (p. 1). Students who are successful self-regulated learners are more likely to make goals and plans for their learning, be motivated and apply effort, know and successfully choose effective learning strategies, review their learning and progress, seek help when needed, and have positive emotions associated with academic learning and content (Zimmerman, 2002). While various conceptions of SRL exist, most ascribe to the underlying belief that learning behavior is goal oriented; when a learner is more successful at modifying their learning behavior, they can more efficiently and successfully reach their learning goal (Moos & Ringdal, 2012).
Despite the strong results realized for student learning, teachers are often not prepared to support SRL in the classroom. SRL is often ambiguous in classrooms and not well understood by teachers (Moos & Ringdal, 2012). Callan and Shim (2019) found that less than 15% of teachers were able to name and describe at least two components of self-regulated learning. Rather, teachers were more likely to describe behaviors associated with motivation and self-monitoring, but almost entirely neglected reflection and planning; two areas that appear ripe with opportunities for application in the classroom. Even so, teachers play an important role in students’ ability to acquire self-regulating skills.
The degree to which teachers implement various features of SRL is related to students’ acquisition of those skills, and various strategies have been successfully used to support both (Moos & Ringdal, 2012). In fact, teachers with a stronger knowledge of SRL are more successful with their implementation of strategies to support SRL (Spruce & Bol, 2015).
Self-Regulated Learning and Effective Teaching
Descriptions of the benefits of SRL are often similar to those of newer, reform-oriented and responsive mathematical practices. For example, Zimmerman (2002) wrote that from an SRL perspective, learning is “as an activity that students do for themselves in a proactive way rather than as a covert event that happens to them in reaction to teaching” (p. 65). Furthermore, the skills and habits of SRL are useful outside the classroom, allowing adults to succeed in the workforce by acquiring new job skills or undertaking large and complex projects (Zimmerman, 2002).
These skills are inherently similar to those used by students in best-practice classrooms with responsive pedagogy, where students are asked to use and develop mathematical practices such as making sense of problems, persevering in problem solving, reasoning abstractly, and using appropriate tools strategically (National Governors Association Center for Best Practices, 2010; Simon, 1995). The ideal student who emerges from such an environment is similar to Zimmerman’s self-regulated learner: students who are intrinsically motivated to learn mathematics, enjoy mathematical tasks, apply strategic efforts, and have more control over their own learning (Boaler, 2002).
Self-Regulated Learning in Mathematics
The TIMSS 2019 assessment framework highlighted mathematics cognitive domains: knowing, applying, and reasoning, with the assumption that each cognitive domain is needed for mathematical competency (Lindquist et al., 2017). These cognitive domains include a range of skills, from recalling definitions for providing mathematical arguments to supporting strategies and, ultimately, allowing students to go beyond simple replication of knowledge. Both SRL and reform-oriented learning environments hold and achieve many of the same objectives. One shared objective is the importance for students to learn to apply procedures (procedural fluency) through exploration of concepts or ideas (conceptual understanding; Huinker et al., 2017), with evidence to support their success in doing so (Callan & Cleary, 2018; Cho & Heron, 2015; Cleary et al., 2017; Palaigeorgiou & Papadopoulou, 2018; Serrano et al., 2019).
Self-regulated learning environments have been shown to increase students’ ability to enjoy mathematics, exercise agency and control over their learning, and ultimately, perform well on assessments (Cho & Heron, 2015; Cleary et al., 2017; Palaigeorgiou & Papadopoulou, 2018; Pape et al., 2003; Serrano et al., 2019). In 2003, Pape et al. documented a teaching experiment with dual goals: to improve both mathematical thinking andself-regulated learning. They found that the teacher participant’s efforts to improve mathematics instruction also increased students’ success in SRL habits and skills (e.g., preparing for tests and an increased sense of control). They wrote, “We argue that implementing mathematics instruction consonant with NCTM standards makes the development of self-regulated learners possible and is at the same time dependent upon some degree of self-regulation within the community of practice” (Pape et al., 2003, p. 179). When immersed in a more effective instructional environment, students were naturally more invested and agentic in their learning without having to make a volitional choice to do so. In this case, both SRL and mathematics goals were met with a more responsive teaching approach.
Effective teacher responsiveness can take a variety of forms, including verbal or written feedback, two methods which may be opportune for SRL environments. Hill et al. (2018) analyzed teaching assistants’ responsiveness to introductory biology students’ lab reports. They were able to demonstrate that being responsive to students’ writing samples through written feedback could enhance student reasoning. Ellis et al. (2019) proposed a framework for supporting students’ reasoning by including the impact of teachers’ verbal response to student reasoning. In their model, they emphasized the importance of a teacher’s move within and between eliciting, responding, facilitating, and extending categories. Maximizing the benefits of both reform-oriented teaching and SRL can further improve the benefits offered by each approach individually, and this approach can increase overall student opportunities for agency, interest, and meaningful learning.
This article describes our examination of the context for understanding teachers’ use of questioning strategies in a self-regulated environment (i.e., a “blended” self-regulated, online environment), as well as their success in providing students with opportunities for sense-making and reasoning. By analyzing teacher questioning and its immediate effect on dialog and student response, we obtained information on the teacher’s role in and experience with integrating responsive teaching into a self-regulated, online environment within the SRL context.
Methods
We used an exploratory, qualitative research design (Patton, 2002) to analyze teachers’ pedagogical approach and actions within an SRL teaching environment. Specifically, we used a content analysis approach (Schreier, 2012) to analyze classroom interactions during self-regulated, online mathematics lessons. This method was useful in analyzing the context of teachers’ questioning, characterizing its frequency and positioning, and describing its effect on the ensuing teacher-student dialog and responses. The following sections provide further detail of our study and design. Participant names, as well as the school name, are pseudonymns.
Context
Data for this study were drawn from a larger research project focused on the implementation of self-regulated, online mathematics units within a rural, Midwestern US school, Fern Elementary. The school adopted the self-regulated learning approach in an effort to personalize and individualize mathematics learning for students in Grades 3 through 8. Classroom teachers designed the self-paced lessons and aligned each to Common Core Mathematics Standards (National Governors Associaiot Center for Best Practices & Council of Chief State School Officers, 2010).
Underlying goals for using a self-regulated learning approach included having students spend more time on concepts of need, collaborating more with peers, and advancing to new concepts when ready. The study was conducted in two separate third/fourth multigrade classrooms. All mathematics instruction (face-to-face and online) still occurred within the context of a designated mathematics time block (i.e., 60-90 minutes) in the physical classrooms. All students had access to a school assigned iPad with internet access. During the mathematics block, students received teacher facilitated minilessons on grade level concepts when needed; however, when the time came to work on individual concepts, students progressed through online videos, activities, and simulations, as well as hands-on tasks to deepen understanding of concepts. During the daily mathematics block, the teacher worked with individuals or small groups of students with similar concept needs.
The blended, self-paced units were created by the grade level teams at Fern Elementary. For the purposes of this study, we focused on the third/fourth-grade units. The teachers met during the summer prior to the study to design and create three online units: geometry, fractions, and measure and data (see Figure 1).
Figure 1
Homepage Access to Self-Paced Online Mathematics Units
A typical unit was structured around the Common Core Mathematics Standards for the grade level and incorporated a variety of technology-based tasks. All lessons within each unit were online and stored using a cloud-based platform. To start a lesson, the students would log on to their iPad. Using a paper guide, they would track their tasks for the lessons. Examples of tasks included watching videos, completing mathematics problems, accessing online information, and utilizing online manipulatives. When students needed to turn in a completed assignment or instructional task, they would submit it to the teacher using the learning management system (LMS).
Participants
Two authors of this paper served as researchers on the larger study, which was the context for data collection. Within the larger study, data were collected in two third/fourth-grade multiage classrooms to analyze teacher and student actions in a self-regulated instructional environment. The classroom teacher participants were purposefully selected due to their common belief and enactment of reform mathematics instruction and involvement in the creation of the online mathematics units. One of the teachers, Jane, was a 2nd-year teacher who had extensive experiences during her university course work at Fern Elementary. The other teacher, Julia, had taught at Fern Elementary for 8 years. Both teachers taught mathematics with a student-centered focus that prioritized procedural understanding through conceptual mathematics learning.
Data Collection
The study participants agreed to video record their mathematics instruction. The teachers wore video-recording glasses or ear-pieces to capture their facilitation of the self-regulated mathematics lessons. The video-recording glasses worn by the teachers allowed researchers to see and hear classroom instruction from each teacher’s perspective. In this way, data were limited to the scope and interactions of the teacher. For more on this method, see Estapa and Amador (2016). Jane and Julia wore the glasses for 3 consecutive days, recording the mathematics instruction each day. On average, a mathematics lesson was approximately 60-minutes in length per day. Each teacher was also asked to write reflections each day on what went well and what challenges were experienced during the implementation of the mathematics lessons taught.
Data Analysis
A content analysis method was selected to explore and analyze instances of responsiveness. Specifically, this method allowed us to construct meaning through analysis and interpretation of instances and context around teacher questions asked within the SRL lesson (Krippendorff, 2018; Schreier, 2012). The teachers’ video data were analyzed in three phases paying special attention to the pedagogical practices the teachers used while facilitating the self-regulated online mathematics lessons. Emphasis was placed on documenting the types of questions teachers asked to understand student responses or build dialogic interaction.
During the first phase of the analysis, two researchers and two other authors of this article transcribed the video recordings and used those transcriptions to identify two units of data: (a) instances of teacher and student interaction and (b) teacher questions. For our purpose, an “instance of interaction” was started when a teacher asked a question to a student or student group, even if it was presumably rhetorical (but meant to elicit student thinking). The instance usually continued as the teacher asked follow-up questions or students volunteered responses (all instances included at least several conversation turns). The instance of interaction ended when the teacher returned to explaining or telling in a way that implied students’ contributions were no longer appropriate. This usually happened when a teacher was ready to start explaining the “right” answer or to switch the students’ attention to a new task or problem.
The purpose of identifying instances of interaction was to include context in our analysis of teacher questioning, rather than viewing each question as an isolated occurrence. We returned to these instances to use them again in the last phase of analysis.
After all the instances of interaction were identified, the same researchers categorized the content of teachers’ questions to determine the focus of the question. This action resulted in more separate data points than the instances of interaction, as one instance of interaction could include many teacher questions. Each teacher question was then coded separately as “product/task” or “thinking,” depending on its content and purpose, and then by level of responsiveness (not, low, or high; see Table 1).
Table 1
Codebook for Teachers’ Questioning
| Code | Definition |
|---|---|
| Product/Task | Related to getting the correct answer, usually on a worksheet or self-paced task. Occasionally, while solving a problem for the class at the board. Includes rhetorical questions related to simple operations (“...and 6 times 5 is what?”). |
| Thinking | Probes a student’s thinking or reasoning. Can be within the context of a particular problem, but it is conceptually-focused rather than procedurally-focused. |
| Not Responsive | Not based on a student’s response or work. Could be an opening question which the teacher would ask of all students, or a procedural one in which they are helping the student to solve the problem the “right” way. Can also be an information-seeking question, where they are evaluating the student’s answer as right or wrong. |
| Low Responsiveness | Must respond to an aspect of the student’s work or a student idea. Also, is either evaluative (indicates whether the student is right or wrong) OR the teacher has an agenda: a correct answer in mind or a leading question to get the student to the right answer. |
| High Responsiveness | Nonevaluative, no leading questions. The teacher is probing student thinking, connecting their ideas, or exploring conceptual significance. |
“Thinking” questions regarded a student’s idea or thinking process (conceptual mathematics), while “product/task” questions were related to a procedure, outcome, or (content-related) management (procedural mathematics). Level of responsiveness was developed using methods described in Lineback (2015), and reflected the extent to which the teacher’s question was responsive to students’ thinking. To be coded as high responsiveness (or simply, “high”), the teacher’s question had to be (a) nonevaluative and (b) regarding a student’s thought or idea (i.e., not a question they would have asked regardless of the student’s contribution).
For example, when the teacher asked a student “Tell me, how did you do the first one?” her question was coded as “thinking, not responsive” because it was regarding student thinking, but it was not in response to the student (and she would have asked the question regardless, as an opener to problem-solving; see Table 2). Later in the lesson, the same teacher said “It looks like you changed this one too. Why did you change your mind from 9 to 90?” Here, she was asking both a thinking question and responding to the student’s work and ideas. It was coded as “thinking, high responsiveness.”
Table 2
Coding Examples
| Code | Not Responsive | Low Responsiveness | High Responsiveness |
|---|---|---|---|
| Product | How many wholes did you write for this one? How do you go from 4 to 36? So, what number would this be? | So, you put 1/8. Which one is like 1/8? Actually, how many wholes is it? | [In response to student answering a measurement question.] It is, and what’s the difference? How are you knowing how to get this in lowest terms? |
| Thinking | Tell me, how did you do the first one? Is there another way I could switch it? [Leading student to correct answer.] | How could you have done this more efficiently? And then how did you figure out the area? | Why did you doubt yourself? Yeah [responding to student], and how can you see? |
These coding decisions were made while viewing the video data and reading the transcripts simultaneously, which helped to provide contextual clues. The project team met weekly during initial coding to assure consensus and stability between coders. When definitions were met at 95% agreement across coders, the researchers coded independently.
The last phase of data analysis focused on the context around the questions. Additionally, frequency and density for questions was coded as either “thinking” or “high responsiveness.” Each question identified in the previous phase was located within its instance of interaction. We used open coding to explore possible purpose and effect. After two rounds of open coding, a final codebook was solidified and used to encode each question. A codebook is provided in the appendix and includes the code name and definition. Analyzing the data in this way allowed us to collect information about how the teachers’ questions related to student reasoning and promoted opportunities for student thinking.
Findings
The purpose of this study was to examine and better understand the use of responsive classroom instruction during the implementation of a self-regulated online mathematics program. Specifically, we investigated the teachers’ questioning and their role in facilitating the teaching and learning processes in an SRL mathematical environment. We first report a global view of how a particular type of SRL, blended instruction (online and face-to-face) was enacted in the two third/fourth multigrade classrooms. Then, findings specific to teacher questioning and responsive teaching are reported.
Self-Regulated Learning Environment
Both teachers appeared to have put considerable thought into how to structure their classrooms for using a self-regulated pedagogy that included both face-to-face and online instructional components. This planning was evident in the class routines and student actions while participating in the self-paced programming, as well as the teachers’ expectations of their students.
In both classrooms, students shared a set of iPads that included enough for 1:1 access, and the devices had specific locations and protocol for charging, use, and care. During each lesson, students mostly spent time with their own device, a related worksheet, or a hands-on instructional activity. Both teachers frequently gathered small groups of students for additional instruction on a topic of difficulty. In addition, Jane opened her lessons with whole group instruction (a discussion format) twice, while Julia began with whole group instruction once in the time observed.
In general, the teachers’ attention was frequently given to moving between individual student needs, their plans for instruction during small group sessions, and occasional whole group instruction time. From the teachers’ perspective (viewed through the video glasses), the whole group instruction time was less distracting and the most focused of the three settings. As opposed to small group or individualized instruction, teachers spent more time talking about one coherent concept and sustained one line of questioning for longer, with fewer overall interruptions during whole group instruction. The teachers also tended to stay in one place in the classroom rather than constantly moving and switching tables (and students), which was common during individual self-regulated time.
Challenges were presented to the teachers when managing the large group of individually paced students. For example, Jane was frequently approached by students and groups of students looking for her help or attention. At times, she was interrupted every 10-30 seconds, causing her to repeat herself and lose her train of thought after returning to the student she was helping.
While moving between tables to check student work (allowing them to check off a particular worksheet), she frequently juggled multiple students and papers. This task was made more difficult since every student was completing a different learning task, requiring Jane to reorient herself to a new concept each time. In comparison to her colleague, Jane’s tone of voice was flat and less energetic, reflecting the difficulty of sustaining concentration and energy during the lesson.
In contrast, Julia had developed a system on the board for each student to record their request for help (by moving a photo of themselves from one area of the board to the other), which allowed her to triage student requests, focus her attention on one student at a time, and keep students at their tables (rather than following her for help). Even with this system in place, she indicated considerable stress and would frequently ask students to self-monitor and make decisions about where they should be or what task they should do, and she continued to monitor classroom activity even while working with a student or student group.
Teacher Questioning Within a Self-Regulated Lesson
To determine how teacher questioning supported responsive teaching, we first analyzed the types of questions the teachers asked. Our findings show that the two teachers asked many questions during the self-paced lessons, between 73 and 136 questions per session. Julia asked nearly two times more student thinking questions than Jane in each lesson, and also had a higher frequency of product/task questions (see Table 3). Based on the frequency of teacher questioning (rather than telling or doing statements), Julia’s lessons had the potential to include more student dialog.
Table 3
Teacher Questioning Frequency During Three Lessons Within Each Class
| Student | Day 1 | Day 2 | Day 3 | Total |
|---|---|---|---|---|
| Student Thinking | ||||
| Jane | 21 | 21 | 19 | 61 |
| Julia | 34 | 40 | 35 | 109 |
| Product/Task | ||||
| Jane | 70 | 52 | 55 | 177 |
| Julia | 69 | 102 | 101 | 272 |
In addition to identifying each question asked, we coded the teachers’ questioning as categorical variables: question type (Product/task = 1, Student Thinking = 2) and responsiveness level (No = 0, Low = 1, High = 2). According to these codes, the highest level of responsiveness that could be reached was the combination of Student Thinking (2) + High (2) = 4, and the lowest level of responsiveness that could be reached was the combination of Product/task (1) + No (0) = 1.
To illustrate the teachers’ questioning and responsiveness in each lesson, visual representations of the variables are presented in radar graphs (see Figure 2). The aim of these descriptive graphs is to visualize the teachers’ questioning patterns throughout each lesson. To construct these radar graphs, we first identified each question with a timestamp showing the exact time of a question. Then, we utilized the numerical codes (sum of the codes for question type and responsiveness level) for each question to get the numerical data to create the graphs.
Figure 2
Teachers’ Questioning Patterns Throughout Each Lesson. Q1: The First Quarter of a Lesson; Q4: The Last Quarter of a Lesson
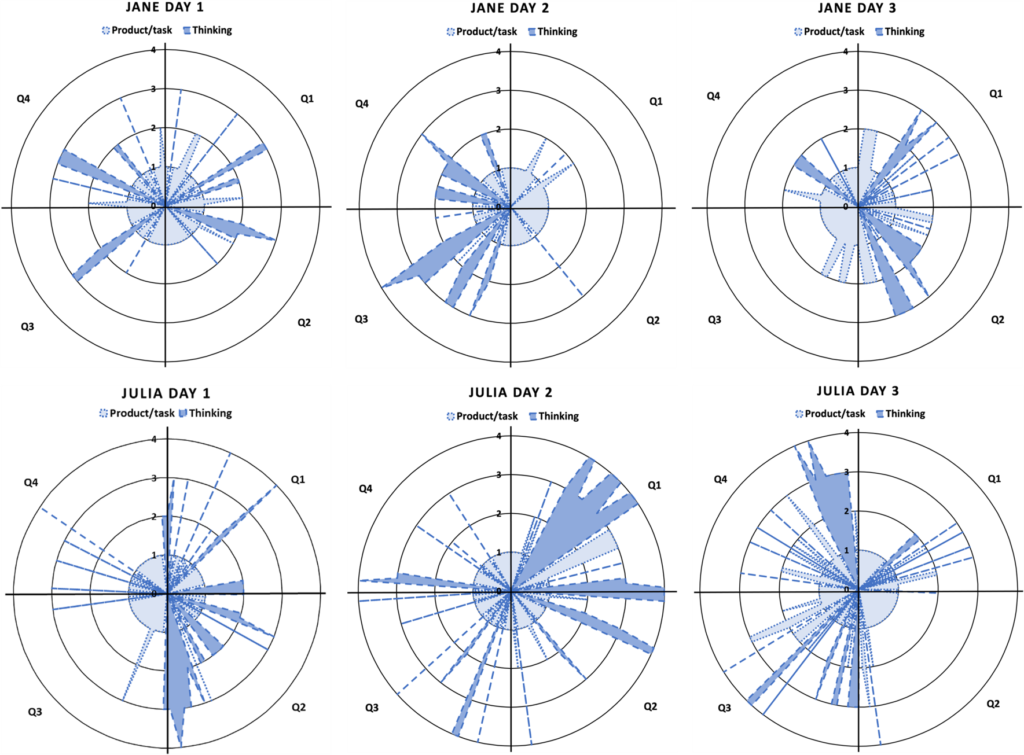
The graphs include only the time with questions, which means that conversations other than questioning are not shown in Figure 2. For example, in Jane’s Day 1, she started questioning with two product/task, not responsive questions (shown in the graph as Magnitude 1 with light blue dotted line). These questions were followed by a student thinking, low responsive question (shown in the graph as Magnitude 3 with darker blue dashed line). Next, three product/task not responsive questions were followed by two product/task, low responsive questions (shown in the graph as Magnitude 2 with light blue dotted line).
Using high-quality teacher questioning as a proxy for responsiveness, these graphs illustrate that Julia was more responsive in her instruction than Jane. In Jane’s lessons, the highest responsiveness level reached was 3 — Student thinking (2) + Low (1) = 3 (n = 27) — with the exception of only one question — Student thinking (2) + High (2) = 4, Day 2. Jane’s Level 4 question was “Why is that true?” However, the conversation did not go further because after this question the student answered, “You need four one-fourths to make a whole,” and the teacher chose not to follow up. She instead asked a rhetorical question, ending the interaction by stating, “And you need four of those right? Awesome. I think that is a great place to stop. That’s fantastic…”
Here, student thinking could have been further developed by asking several follow-up questions, possibly a student thinking question such as, “Why do you use one fourth as a fraction?” With further follow-up and questioning regarding the students’ own ideas, Jane may have had more opportunity to support or further develop student reasoning.
In Julia’s Day 1, the first half of her lesson was more highly responsive than the second half. Conversely, in Julia’s Day 3, in the second half of the lesson she seemed more responsive in terms of teacher questioning. In the first half of the Day 1, Julia asked several high level student thinking questions, such as “…How’d you get that so quick Abby?” and “It is, and what’s the difference?” to stimulate students’ ideas on multiplication. However, the second half of the lesson was based on mostly product/task questioning, such as, “So how many 9’s in 72?” In Day 3, the first half of the lesson had product/task and student thinking low or no level. The second half of the lesson looked more responsive due to several high- and low-level student thinking questions.
We assume that these imbalanced frequencies were due to the self-regulated nature of the lessons. On the other hand, Julia’s second lesson looked more balanced when comparing the first and last quarter of the lesson. In particular, the first quarter of the second lesson had longer conversation with more high-level student thinking questioning. These longer conversations required high responsive questions from the teacher, such as “Interesting, why did you change your mind?” “Now this group, if you see it like this — now what are you thinking?” and “Cause you’re right; but how could you know for sure?” This kind of questioning contrasted with the limited, lower frequency questioning used by Jane.
Sustained Questioning Related to Student Thinking
The imbalance in frequency of thinking, high categories also had an impact on the amount of time teachers sustained valuable questioning patterns (see Table 4). Julia was not only more likely to use questions coded as thinking in her teaching, but she was also more likely to ask one thinking question after another, sustaining the amount of time students spent problem-solving or engaged in valuable reasoning.
Table 4
Teacher Time in Questioning Related to Student Thinking
| Session | Jane | Julia |
|---|---|---|
| Day 1 | 35 seconds | 57 seconds |
| 28 seconds | 44 seconds | |
| 36 seconds | ||
| 27 seconds | ||
| Day 2 | 140 seconds | 208 seconds |
| 69 seconds | 22 seconds | |
| 28 seconds | 123 seconds | |
| 19 seconds | ||
| Day 3 | 132 seconds | 33 seconds |
| 40 seconds | 23 seconds | |
| 31 seconds | 160 seconds | |
| Total | 503 seconds (8.3 minutes) | 752 seconds (12.5 minutes) |
| Note. The number of seconds each teacher sustained consecutive thinking questioning, defined as three or more teacher questions coded as thinking. Questioning sessions during group discussion time (rather than tutoring during student work time) are bolded. | ||
Across the span of all three mathematics lessons, Julia spent 12.5 minutes total with continuous thinking questioning, while Jane spent 8.3 minutes. For both teachers, each sustained thinking questioning session was, on average, 60 seconds. While we do not propose that teachers should be continuously questioning their students, this finding does reveal the overall brevity of responsive questioning related to student thinking and the frequency with which teachers are able to suspend their concrete guidance in favor of questioning strategies. In addition, roughly one-third of each teacher’s instancesof questioning sessions occurred during group discussion. Since this time is less than the proportion of classroom time spent in group discussion, it suggests that there may be a greater likelihood of sustained questioning sessions during group discussions (rather than tutoring).
Teacher Pedagogical Approaches Within a Self-Regulated Lesson
Next, we examined the student and teacher responses around teacher questioning to build a contextual understanding of how teacher questioning contributed to responsive teaching practices — and ultimately, the potential for students to engage in more thinking and reasoning. We found that the level of responsiveness may have depended on the teachers’ perception of the purpose of an SRL environment and their own lesson objectives. This thinking is reflected in the teachers’ questions as well as the outcome in student responses. Julia used the time around self-regulated instruction to provide opportunities for student reasoning, while Jane used the time to help students rehearse and master procedures related to their self-paced lessons.
This difference between the two teachers can be seen in their use of similar questions, especially the cognitively valuable thinking, high questions. At face value, the questions initially appear similar (see Table 5): “Okay, so tell me how you went through that process” and “Can you explain what you drew?” Both required students to explain their thinking and describe the problem-solving process. Yet, each question may have a different level of responsiveness depending on (a) whether it was in response to a student’s (or students’) ideas, and (b) whether it invited further opportunities for student thinking. In the excerpts that follow (Table 5), both teachers used questioning that we have coded as thinking.”
Table 5
Examples of Teachers’ Questions Labelled “Thinking” and “High Responsiveness” or “Thinking” and “Low Responsiveness”
| Teacher Questioning | Jane | Julia |
|---|---|---|
| Questions labelled as both thinking and high responsiveness | Why is that true? | Yeah, and how can you see? Why did you doubt yourself? Why’d you change your mind from 18? Derek, can you share why you thought this one was true? Oh, Sayla says you’re not supposed to switch both of them. How come? You’re right - but how could you know for sure? Hm. How can you know for certain? |
| Questions labelled as thinking and low responsiveness | Alright, let’s look at what Calvin did. Can you explain what you drew? I want you to prove it. Think about what Maddy did to prove it. | Did anyone make that to be true? Nice, because what do you know about 6 times 4? Okay, so tell me how you went through that process. How did you figure out the area? |
| Note. Jane had only one quote which was coded as thinking and high responsiveness. | ||
However, in the transcript from Julia’s classroom, the teacher’s questions were responsive to students’ thoughts and ideas, without an obvious agenda or evaluation of student answers. They also invited further thinking from the students.Students were in a large group, talking about their ideas to one another. Then Julia got the class’s attention as she noticed a certain group.
Julia: I want to first ask this group because I saw them get up and go get a pencil [to work something out]. That happens all the time with mathematicians [when they] are talking to each other. What happened in that group can you tell me?
Student: We looked at…. [inaudible]
Julia: Oh, you looked at the Number 1 again. Did you all think that Number 1 is true?
[multiple students responded “yes”]
Julia: And now all you three think that it’s false? Interesting, why did you change your mind?
Students: [Inaudible]
Julia: [Repeating what students said to understand it.] It’s 8 times 6. Oh! You’re saying this would turn into 8 times 6? Hmm. Can I hear some other thoughts? Someone who would like to disagree with the false?
Ivan: Um, it’s sort of switched around…[inaudible]
Julia: Okay so Ivan, you’re saying it would still be the same if I wrote it like this? What property tells me thats true? [Inaudible student murmuring.] Yeah! Commutative property of multiplication. Now this group, if you see it like this [gestures to the flipped equation on the board], now what are you thinking? Do you like it more that way? Or do you still think it’s false? Anyone else think this is true that wants to disagree?
Certainly, Julia reached a learning goal: helping her students to explore concepts of equality, multiplication, and the commutative property of multiplication. Yet, she drew out student thinking and helped students to compare their ideas to one another’s ideas, centralizing student ingenuity rather than a procedure. She treated the exercises as opportunities to explore novel programs and generate new problem-solving methods. She also asked students to practice material that had previously been covered, but she did so in a less prescriptive manner.
In contrast, Jane used questioning to remind students of a procedure. Even when the questions were oriented to student thinking (and, therefore, coded as thinking), her ultimate goal was still correct use of the procedure or language. In the following excerpt, this assertion is evidenced by Jane correcting the student’s language use (she rephrased his explanation in “pieces of a whole” language), and short wait times. She also called Calvin up to the board specifically to use his thinking as an example of the correct way to solve the problem, rather than an idea for students to reason with. Interestingly, she continued to use the problem-solving language (“…did he just provide it to you? Do you agree with him now?”), but did not indicate that these questions were actually important, or that the students’ ideas held authority. As this conversation began, students were seated at the floor, and Jane called them up one at a time.
Jane: Alright let’s look at what Calvin did. Can you explain what you drew?
Calvin: Um, this is one fourth. It’s a whole just with one quarter.
Jane: How many pieces are in your whole?
Calvin: One.
Jane: You shaded one, but how many in total?
Calvin: Four.
Jane: ‘Kay.
Calvin: This is four fourths, because the four fourths are just one whole.
Jane: Okay…I agree with you.
Calvin: And then four over one is four wholes.
Jane: Okay. If you weren’t sure if you agreed with Calvin, did he just prove it to you? Do you agree with him now? [Waits less than a second.] Okay, snaps for Calvin. [Calvin goes back to seat.]
The contexts of these SRL environments were physical classrooms where students were individually working on self-paced online mathematics lessons unless called to participate in small group or whole group instruction or even individual tutoring sessions. Within these contexts, the teachers were asked to organize and manage these multifaceted learning environments while still implementing instructional routines and making instructional decisions that would allow them to be responsive to students’ needs. As illustrated in the examples provided, some SRL self-paced technology environments can be used for review and practice purposes: Jane achieved these goals as she encouraged students to remember the procedures, return to their notes to review, and relearn material by watching instructional videos at their level, as needed.
On the other hand, it appears that when using this approach, Jane was not as effective at giving students opportunities for reasoning. Rather, she did the reasoning herself by making the connection between parts, wholes, denominators, and models, and then asking students to recall components of that connection. This approach was a stark contrast to Julia’s encounters with students, when she asked them to do the reasoning.
In summary, our findings indicate that both teachers asked many questions of varying types. However, the ways such questions supported responsive practice varied. The results of our study reveal three main ideas specific to SRL teaching practices, which are discussed in the next section.
Discussion
In our study, we wanted to better understand SRL implementation within the elementary classroom. Specifically, we analyzed the questions teachers asked and the use of responsive practice across the lessons. A key learning from our study is that while the teachers asked many questions within the SRL mathematics lessons, there was a variable rate of responsiveness between the two teachers who participated in the study. We know that responsive teaching supports student learning, but what impact does such variability play on opportunities for learning? Specific to this study, the overall amount of time teachers questioned or were responsive to student thinking was low. This result brings up critical questions concerning the extent to which self-regulated learning can support responsive learning environments: How can SRL and reform-oriented pedagogies support one another, and how do teachers structure their instructional decisions to incorporate both approaches?
The consistent factor in the work presented here is the teacher. This study documented how two teachers can approach self-regulated learning in different ways, with different purposes and orientations. However, more research is needed on how teachers distinguish between a student’s mathematical procedural and conceptual needs, understand the benefits of SRL versus other strategies, and ultimately make decisions about how, when, and why a self-regulated strategy should be used. For example, how might a teacher identify students who require SRL supports as compared to other educational challenges? It is likely the teacher’s role and decision-making impacts student learning experiences, but what impact does this have on academic achievement?
Additionally, our findings pointed out that teachers have a unique perspective when approaching technology-mediated SRL. Rather than relying on knowledge about the technology or the students’ experiences with it (aside from the basics, of course), the teachers in our study had to navigate the following: logistical challenges of providing educational support to a classroom full of unique children; instructional decisions regarding small group, large group, or individual tutoring/work checking time; and more theoretical quandaries such as how to best move students’ through the mathematics lessons, while simultaneously supporting their conceptual development. This aspect of self-regulated learning is not about the technology. Rather, the work of teaching becomes pivotal, in that some student thinking subsides in the technology and, therefore, requires more or different elicitation.
Research indicates that in classrooms with responsive teachers, students are more likely to engage with material and have a sense of ownership to it. Our second key finding hinges on the idea that teachers’ responsiveness to student thinking increases students’ sense of agency (as also in Ardasheva et al., 2015; Schoerning et al., 2015).
Schoerning et al. (2015) studied teachers’ language behaviors similar to those we observed in the present study. They measured teacher language behaviors, such as frequent dialog interchange and summarizing student talk before further commenting, and found that an increased frequency in these behaviors led to stronger student language use and dialog around content topics. They hypothesize that,
In the absence of teacher speech bearing authority markers such as low tone and slow tempo, or in the presence of relaxed, nonauthoritarian body language, students may feel less concerned about being punished or corrected by authority figures. This gives them greater opportunity for agency. … Similarly, a teacher who values the content of student speech above the vocabulary used in student speech, or a teacher who allows students to speak without formal permission, creates a similar avenue for agency. (p. 254)
Similar to the teachers in Schoerning et al.’s (2015) study, Julia had more frequent extended periods where students dialogued freely. Furthermore, she often referred and responded to student ideas when holding group discussion. Additionally, she was less likely than Jane to evaluate students’ ideas or ask them to redo a procedure using certain language or steps. Even from our data focused on the teachers’ perspective, decreased evaluation appeared to increase students’ participation and ownership in the dialog, much like it did in Schoerning et al.’s study.This dynamic may be of interest in future studies. Whatimpact does student agency have on the success of an SRL environment? How is this dynamic sustained, and is student achievement increased as a result?
More research is needed to understand the role of SRL in responsive classrooms and to determine if the efficacy of SRL changes in a traditional versus responsive classroom. Our results indicate that research in this area could be a promising way to maximize the benefits of both SRL and responsive teaching and further elucidate the impacts on student learning and engagement.
Our final key finding supports research highlighting that teaching within an SRL environment draws on a teacher’s knowledge of content and pedagogy (Barr & Askell-Williams, 2020). Our findings extend this idea to draw attention to the relevancy of teacher- and school-level pedagogical goals. For example, this school district had a goal for implementation that did not completely mirror the same teaching philosophy of the classroom teachers involved. The district goal for SRL was for students to spend more time on concepts of need, allow collaboration with peers, and advance to new concepts when ready, all through the use of individualized instruction supported by technology, videos, and step-wise worksheets or hands-on activities. Thus, it is difficult to discern whether district administrators see the purpose of the implementation of SRL as procedural (recalling and memorizing information or procedures they may have missed) or conceptual (giving students time and space to reason with the concepts they most needed to understand).
This lack of clarity may have reached the participants of our study as well, as both teachers used different approaches to reach the district goals with students. Jane encouraged students to recall and review procedural information and helped students use technology as a tool for self-management and independent learning. Alternatively, Julia’s conceptual orientation to the classroom environment increased students’ opportunities for reasoning with the self-regulated environment, but it is unclear whether those goals are congruent with her colleagues’ goals or those of the district in implementing a self-paced mathematics program.
What do teachers have to do to take full advantage of blended, self-regulated instruction and make it effective? We also see tension between these goals in Figure 2, which illustrates the differences between teachers’ experiences across the study. As the figure illustrates, Jane had longer conversations in procedural questioning and Julia had longer conversations in conceptual questioning. This tension indicates that goals and orientations can affect the related responsiveness in teacher questioning.
Jane’s and Julia’s understandings of SRL may have had an impact on their ability to use the online, self-paced mathematics units in ways that were responsive to student thinking. Previous research demonstrates that teachers do not always have a clear understanding of SRL, nor useful methods to help students develop SRL (Callan & Shim, 2019). Without knowledge of the components of SRL and its intermediary skills, teachers likely require additional training to thoroughly understand and support students’ SRL (Spruce & Bol, 2015). Further research is needed to understand this dynamic, as well as how SRL can support the vision of reform mathematics instruction and how effective teaching practices are implemented in blended (i.e., face-to-face and online) contexts. The global pandemic revealed the importance of technology in learning environments. However, better understanding for teaching approaches within these environments will support teaching and learning across the face-to-face and online platforms.
Conclusion
The purpose of this study was to examine how the teachers’ use of questioning was an indicator of responsiveness during the implementation of a self-regulated, online mathematics program in elementary classrooms. Specifically, we investigated what type of questions teachers ask during SRL lessons and how they actualize responsive teaching in a self-regulated learning environment. This study highlights the complexity of the challenges associated with managing a classroom of individually paced students with regard to a teacher’s ability to be responsive to their instructional needs. It is critical for teachers to have a clear understanding around the purpose of an SRL environment, as teachers’ questioning and responsiveness may impact how students engage with and own the content being taught.
As technology continues to innovate classroom instruction and delivery, it is critical that we understand not only how to support student learning experiences, but also the teacher’s pedagogical approach situated in such technology-rich contexts. Further, as self-paced learning occurs outside of school contexts (i.e., online learning or hybrid learning) more understanding of ways to prepare and support teachers within this format is necessary.
Understanding how reform mathematics teaching, specifically responsive teaching, was evident in an SRL setting affords insight into what future supports are needed for teacher learning and what are acceptable expectations for mathematics instruction in blended learning contexts. This understanding will inform teacher education programs to better support learning to teach with technology in blended environments using responsive approaches. Now, more than ever, this understanding is critical as teaching and learning innovations are realized that utilize SRL environments.
References
Ardasheva, Y., Norton-Meier, L., & Hand, B. (2015). Negotiation, embeddedness, and non-threatening learning environments as themes of science and language convergence for English language learners. Studies in Science Education, 51(2), 201-249. doi:10.1080/03057267.2015.1078019
Barr, S., & Askell-Williams, H. (2020). Changes in teachers’ epistemic cognition about self–regulated learning as they engaged in a researcher-facilitated professional learning community. Asia-Pacific Journal of Teacher Education, 48(2), 187-212.
Boaler, J. (2002). Experiencing school mathematics: Traditional and reform approaches to teaching and their impact on student learning. Routledge.
Callan, G. L., & Cleary, T. J. (2018). Multidimensional assessment of self-regulated learning with middle school math students. School Psychology Quarterly, 33(1), 103–111. doi:10.1037/spq0000198
Callan, G. L., & Shim, S. S. (2019). How teachers define and identify self-regulated learning. The Teacher Educator, 54(3), 295-312.
Carpenter, T., Fennema, E., Franke, M. L., Levi, L., & Empson, S. (2000, September). Cognitively guided instruction: A research based teacher professional development program for elementary school mathematics (Research Report No. 003). Wisconsin Center for Education Research.
Cheung, A. C. K., & Slavin, R. E. (2013). The effectiveness of educational technology applications for enhancing mathematics achievement in K-12 classrooms: A meta-analysis. Educational Research Review, 9, 88-113. doi:10.1016/j.edurev.2013.01.001
Cho, M.-H., & Heron, M. L. (2015). Self-regulated learning: The role of motivation, emotion, and use of learning strategies in students’ learning experiences in a self-paced online mathematics course. Distance Education, 36(1), 80-99. doi:10.1080/01587919.2015.1019963
Cleary, T. J., Velardi, B., & Schnaidman, B. (2017). Effects of the self-regulation empowerment program (SREP) on middle school students’ strategic skills, self-efficacy, and mathematics achievement. Journal of School Psychology, 6(4), 28–42.
Ellis, A., Ozgur, Z., & Reiten, L. (2019). Teacher moves for supporting student reasoning. Mathematics Education Research Journal, 31, 107-132.
Estapa, A., & Amador, J. (2016). Wearable cameras as a tool to capture preservice teachers’ marked and recorded noticing. Journal of Technology and Teacher Education, 24(3), 281-307.
Estapa, A., & Nadolny, L. (2015). The effect of an augmented reality enhanced mathematics lesson on student achievement and motivation. Journal of STEM education, 16(3), 40-48.
Fitzgerald, M. S., & Palincsar, A. S. (2019). Teaching practices that support student sensemaking across grades and disciplines: A conceptual review. Review of Research in Education, 43(1), 227-248.
Gould, D., & Schmidt, D. A. (2010). Trigonometry comes alive through digital storytelling. Mathematics Teacher, 104(4), 296-301.
Hammer, D., Goldberg, F., & Fargason, S. (2012). Responsive teaching and the beginnings of energy in a third-grade classroom. Review of Science, Mathematics and ICT Education, 6(1), 51-72.
Hill, C., Gouvea, J. S., & Hammer, D. (2018). Teaching assistant attention and responsiveness to student reasoning in written work. CBE Life Sciences Education, 17(2), ar25. doi:10.1187/cbe.17-04-0070
Huinker, D., Bill, V., & Smith, M. S. (Ed.). (2017). Taking action: Implementing effective mathematics teaching practices in K-Grade 5. National Council of Teachers of Mathematics.
Jacobs, V. R., Lamb, L. L. C., & Philipp, R. A. (2010). Professional noticing of children’s mathematical thinking. Journal for Research in Mathematics Education, 41(2), 169–202.
Krippendorff, K. (2018). Content analysis: An introduction to its methodology. Sage.
Lineback, J. E. (2015). Methods to assess teacher responsiveness in situ. In A. D. Robertson, R. Scherr, & D. Hammer (Eds.), Responsive teaching in science and mathematics (pp. 221-244). Routledge.
Lindquist, M., Philpot, R., Mullis, I. V. S., & Cotter, K. E. (2017). TIMSS 2019 Mathematics Framework. In I. V. S. Mullis & M. O. Martin (Eds.), TIMSS 2019 assessment frameworks (pp. 11-25). http://timssandpirls.bc.edu/timss2019/frameworks/
Mishra, P., & Koehler, M. J. (2006). Technological pedagogical content knowledge: A framework for teacher knowledge. Teachers College Record, 108(6), 1017-1054.
Moos, D. C., & Ringdal, A. (2012). Self-regulated learning in the classroom: A literature review on the teacher’s role. Education Research International,2012,1–15.
National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematics success for all. Author.
National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common core state standards for mathematical practice. Author.
Palaigeorgiou, G., & Papadopoulou, A. (2018). Promoting self-paced learning in the elementary classroom with interactive video, an online course platform and tablets. Education and Information Technologies, 24(1), 805-823. doi:10.1007/s10639-018-9804-5
Panadero, E. (2017). A review of self-regulated learning: Six models and four directions for research. Frontiers in Psychology, 8, 422. doi:10.3389/fpsyg.2017.00422
Pape, S. J., Bell, C. V., & Yetkin, İ. (2003). Developing mathematical thinking and self-regulated learning: A teaching experiment in a seventh-grade mathematics classroom. Educational Studies in Mathematics, 53(3), 179-202. doi:10.1023/a:1026062121857
Patton, M. Q. (2002). Qualitative research and evaluation methods. Sage.
Richards, J., & Robertson, A. D. (2015). A review of the research on responsive teaching in science and mathematics. In A. D. Robertson, R. Scherr, & D. Hammer (Eds.), Responsive teaching in science and mathematics (pp. 54-73). Routledge.
Schoerning, E., Hand, B., Shelley, M., & Therrien, W. (2015). Language, access, and power in the elementary science classroom. Science Education, 99(2), 238-259. doi:10.1002/sce.21154
Schreier, M. (2012). Qualitative content analysis in practice. Sage.
Serrano, D. R., Dae-Ayuela, M. A., Gonzalez-Burgos, E., Serrano-Gil, A., & Lalatsa, A. (2019). Technology‐enhanced learning in higher education: How to enhance student engagement through blended learning. European Journal of Education, 54, 273-286.
Simon, M. A. (1995). Reconstructing mathematics pedagogy from a constructivist perspective. Journal for Research in Mathematics Education, 26(2), 114-145. doi:10.2307/749205
Spruce, R., & Bol, L. (2015). Teacher beliefs, knowledge, and practice of self-regulated learning. Metacognition and Learning, 10(2), 245-277.
Tondeur, J., Van Braak, J., Ertmer, P. A., & Ottenbreit-Leftwich, A. (2017). Understanding the relationship between teachers’ pedagogical beliefs and technology use in education: A systematic review of qualitative evidence. Educational Technology Research and Development, 65(3), 555-575. doi:10.1007/s11423-016-9481-2
Zimmerman, B. J. (2002). Becoming a self-regulated learner: An overview. Theory Into Practice, 41(2), 64-70.
Zimmerman, B. J., & Schunk, D. H. (2011). Self-regulated learning and performance. In B. J. Zimmerman & D. H. Schunk (Eds.), Handbook of self-regulation of learning and performance (pp. 1-12). Routledge.
Appendix
Final Codebook To Encode Teacher Questioning Related To Student Thinking
| Code | Definition |
|---|---|
| asks student to recite information | Simple recall question |
| building consensus on big idea | Uses student ideas or teacher’s own information to help build consensus around a main goal of the lesson. Different from connecting student ideas, because this is not just connecting ideas for problem-solving, it’s moving toward an answer based on student ideas and how the lesson or group discussion has gone. The teacher's goal in these comments is to help students grasp the big idea. |
| checking for understanding | Asks a question that helps teacher evaluate students’ understanding |
| collecting ideas | Asks students to share ideas, collects a variety of student thoughts. |
| connecting student ideas | Points out connections between student ideas. Differs from consensus building for the reasons above – also usually has less teacher talking time and teacher more frequently defers to students after making a connection between ideas. |
| explain your thinking | Teacher asks student to explain their thinking |
| interest in student ideas | Reserved for teacher’s expression of interest in student ideas. “That’s so interesting!” “Oh, I'm glad you told me that!” “I love the way you decided to do that.” Is separate from student agency because it’s not simply giving students choice or responding to their ideas – it’s a plain expression of understanding and paying attention to student thinking. |
| leading question | Asks student a question that clearly has a right answer but gets them to the next step in a procedure. Ex: “Okay, and 2 + 5 is what? And then multiply that times 3 and you get what?” |
| non evaluative | The teacher follows up a student idea with a nonevaluative response. |
| probing student thinking | Teacher asks follow up questions to reason with the students’ idea. It is not for purpose of their own evaluation of students’ thinking (checking for understanding), and they are not asking a general explanatory question (explain your thinking). Ex: “Why does it have to be an even number?” |
| student agency | Used when the teacher gives an option or choice to students, if she recognizes their individual way of doing it as valid or recognizes their autonomy. “Do you like it better like that?” (referring to rearranging a mathematical expression), “Do you want to multiply these first or these ones first?” |
| using student idea to get right answer | Refers to student’s idea to present a concept, rather than positioning themselves as knowledge-holder. |
![]()