Dynamic geometry software is a powerful tool that can be used to explore geometric relationships, conjecture, and test hypotheses (Sinclair, Skelin, & Pimm, 2012). However, the potential of this tool for enhancing the mathematics classroom is mediated by the ability of teachers to select tasks that take advantage of the unique features present in dynamic geometry environments and build sketches that make salient, specific mathematical properties for students. While this tool has great potential to enhance mathematics classrooms, it is reliant on teachers’ ability to build sketches that can efficiently and effectively highlight mathematical relationships.
Teacher educators have a unique opportunity to build experiences into teacher preparation programs that allow beginning and preservice teachers to think critically about the benefits and challenges afforded by technology to enhance students’ learning of mathematics (Brakoniecki, Glassmeyer, & Amador, 2016). Using dynamic geometry software in the classroom requires teachers to draw upon their knowledge of content, pedagogy, and technology in new ways.
In looking at the ways teachers build their own sketches and examining how their constructions highlight certain relationships, teacher educators can support teachers to further develop their knowledge of the teaching and learning of mathematics with technology. Thus, the study described in this paper explored the range of dynamic geometry sketches produced by preservice teachers in a mathematics content course for secondary teachers. We highlight here the challenges beginning teachers face as they seek to build mathematically accurate and illustrative sketches.
By better understanding issues in teachers’ construction of sketches, we can identify opportunities to help teachers bring together their knowledge of mathematics, pedagogy, and technology into a richer technology, pedagogy, and content knowledge (TPACK; Mishra & Koehler, 2006).
Technology to Support the Learning of Mathematics
The complex interactions between mathematical subject matter, technological tools, and instructional approaches require thoughtful and purposeful consideration in implementation. Strategic knowledge is required to operationalize the interaction of these domains. Mishra and Koehler (2006) advanced a framework to describe these interactions with their TPACK framework. They argued, much as Shulman (1986) did when proposing pedagogical content knowledge, that the effective teaching of content with technology requires not just an interaction of disparate domains of knowledge, but instead a specialized knowledge pertinent to how the teaching and learning of a subject can be affected by technology.
They argued that in teaching content with technology, teachers draw upon their knowledge of content, pedagogy, and technology. However, they argued for a unique knowledge in the combination of these domains that is distinct from having knowledge of any individual domain. Building upon the work of Shulman, these domains are pedagogical content knowledge (e.g., knowing common misconceptions of students when learning multidigit multiplication), technological content knowledge (e.g., knowing that a particular graphing calculator does not show holes in the visual display of a discontinuous function), technological pedagogical knowledge (e.g., knowing that a piece of classroom software features teacher controls that can capture student work simultaneously, which can then be shared out for the class to examine), and technological pedagogical content knowledge (e.g., knowing how that a geometry software allows for a function to be simultaneously represented in graph, table, and equation form, so that patterns of change can be observed with changing a coefficient of a function). When using dynamic geometry software in the classroom, teachers are often required to draw upon many or all of these different domains of knowledge to think about how the software can make visible mathematical relationships and the observations and generalizations that students might make when interacting with the sketch.
Visual representations are a critical component of geometry. Teachers and students frequently work with diagrams in geometry (Sinclair et al., 2012) and negotiate how to interpret and read these constructions. The creation of these diagrams highlights certain mathematical relationships.
Although static diagrams often present a figure in one arrangement, dynamic diagrams can be thought of as a presentation of a figure in many arrangements (Sinclair, Healy, & Sales, 2009). By dragging objects in dynamic diagrams, students create numerous diagrams in rapid succession. Through this use of dynamic movement, students can become emphatically convinced of mathematical relationships based on the appearance of a diagram and use that visual certainty in their reasoning about mathematical phenomena.
One limitation of physical diagrams is that usually only see the finished product can be viewed, not its construction; however, geometry software allows users to highlight or uncover how sketches came to be produced. These sketches are often designed in parent-child relationships (e.g., a line being constructed through two existing points or a ray constructed to bisect an existing angle). Users can trace through the lineage of sketches to uncover how a sketch operates, learning what parts of these diagrams are dependent on other parts and learning what a sketch attempts to represent. This technological pedagogical understanding can be an important tool for learning about a diagram beyond just how it looks, but what it represents.
In addition to the importance of working with diagrams, the study of geometry also includes heavy emphasis on the focus of variance and invariance (Sinclair et al., 2012). Geometric theorems and properties often highlight what changes with each other (e.g., interior angle measures as the number of sides of regular polygons increase) and what stays the same as other dimensions vary (e.g., diagonals of a rhombus remain perpendicular bisectors of each other, no matter the rhombus).
Known relationships can be used to explore and explain new relationships. These variant and invariant relationships become highlighted in dynamic geometry environments, as the dynamic movement of figures, lines, and points allows certain variance while maintaining other invariance. For example, drawing a rectangle requires the content knowledge that opposite sides are parallel and all interior angles are at 90º. When building a dynamic sketch of a rectangle, it must be constructed in such a way that the movement of points maintains these features, which incorporates a technological content knowledge. The four vertices of the rectangle cannot all be independent points; otherwise, the movement of one point could make opposite sides no longer parallel or interior angles no longer 90º.
A sketch constructed to always be a rectangle highlights certain variances and invariances through the manipulation of the sketch. This is different than a sketch of a parallelogram, which can be manipulated into a rectangle that can highlight other variances and invariances, depending on which objects are made independent and dependent.
When interacting with static diagrams or dynamic geometry sketches, students are often asked to use the figures to explore a mathematical phenomenon. Some activities are possible with figures whether they are static or dynamic, such as drawing, measuring, or constructing within a given sketch. The tools to perform these actions vary and have different degrees of accuracy, but similar observations and outcomes are possible. However, dynamic geometry sketches have the ability to have objects dragged, transformed, and animated, allowing students to consider multiple examples, notice variant and invariant relationships, and even be surprised by emerging patterns (Trocki, 2014).
These types of activities are challenging, time consuming, and maybe even impossible to do with hand-drawn figures. The power of dynamic geometry sketches lies in the ability to manipulate and consider the different relationships of figures and requires teachers to draw upon their technological pedagogical content knowledge when designing these experiences for students.
In addition to highlighting properties of geometric relationships, the use of dynamic geometry software also allows for opportunities to change the kinds of geometry tasks offered to students. Hughes, Thomas, and Scharber’s (2006) Replacing, Amplifying, and Transforming (RAT) framework identifies how different tasks with technology change (or do not) the nature of the mathematics under consideration. Tasks that are (nearly) identical to their paper-and-pencil versions often just replace the analog task with a digital environment, requiring identical thinking and understanding. Sometimes the technological environment offers increased efficiency and productivity to a mathematical task. In these cases, the technology is described as amplifying the mathematical tasks of the classroom. A transformation through technology occurs when the technology changes the instructional method or the actual subject matter (Hughes et al., 2006). The RAT framework, thus, offers a mechanism to characterize the role technology has upon a mathematics task.
To this end, we sought to explore the ways in which preservice teachers built dynamic geometry sketches and to describe the variations of their constructions for how they highlighted or obscured certain variant and invariant mathematical relationships. We next describe an activity in which preservice mathematics teachers were asked to create dynamic geometry sketches and present some examples of their sketches. Our intent is to illustrate some common difficulties that occur when trying to create dynamic geometry sketches so that we can help teachers expand their knowledge and understanding of how their constructions may or may not make visible intended mathematical relationships.
Slope and Angle Activity
The preservice teachers from which we draw our examples came from two sections of a mathematics content course for preservice secondary teachers at a large university in the United States (31 preservice teachers across 2 years). This content course focused on algebra, geometry, and trigonometry.
During one series of activities in this class, the preservice teachers investigated the relationship between the slopes of lines on the coordinate plane and the angles these lines made with respect to the x– and y– directions (the tangent relationship). What was unique for this activity was that the preservice teachers were not told that this was the tangent relationship when they began the task.
The activity has the preservice teachers investigate this relationship for lines through the exploration of slope triangles (right triangles with their hypotenuse on the line). The preservice teachers initially explored with paper and pencil, using the grid lines of graph paper to approximate slope ratio of the lines with the triangles and a protractor to measure angles to the nearest degree of the triangles. Early in the activity, the preservice teachers conjectured that all of the slope triangles of a line are similar to each other, meaning that corresponding angles of the triangles are congruent and the lengths of triangles remain proportional to each other.
Near the beginning of the activity, the preservice teachers were asked to investigate a line that made an 11º angle with the x-axis and a different line that had a slope of 2/5. The preservice teachers noticed that lines with an 11º angle (when rounded to the nearest degree) had a slope of approximately 1/5 and that lines with a slope of 2/5 had slope triangles with base angles of 22º (when rounded to the nearest degree).
The preservice teachers conjectured that this apparent linear pattern between the slope and the angle would continue. That is, they suspected that when the angle is doubled, the slope also doubles. However, after some thinking, some of the preservice teachers identified a potential problem with this apparent linear relationship, noting that if it were true, a line with a slope of 5/5 should correspond to 55º angle right triangles, but some knew a line with the slope of 5/5 should have 45º angle right triangles.
Although they understood that their conjecture broke down when they thought about larger angles, they did not understand why it broke down. To help them explore why their initial hypothesized relationship might not hold, the instructor (the third author of this paper) assigned the preservice teachers the following instructions to create dynamic geometry sketches that allow for the exploration of the angle and slope relationship for homework.
Use Geogebra (geogebra.org), Desmos (desmos.com), or Geometers’ Sketchpad (www.dynamicgeometry.com/) to create two files. These files should be dynamic in that you can click and drag a point to get different slope triangles. Make sure the side length and height is displayed. Your first file should contain the 11 degree angle similar to graph shown on the first page of the in-class activity. Your second file should contain a graph of the line y = (2/5)x with many different slope triangles, similar to problem 4a. Your sketch should include an explanation of what angle is formed between this line and the 3 o’clock position of the x-axis.
The instructor had several goals with this assignment. First, it was an opportunity for the preservice teachers to utilize the dynamic aspect of the software, where they could draw and manipulate a slope triangle with dynamic angles and side lengths to help show that no matter the size or location of the slope triangle, the side lengths remained proportional and, thus, the slope ratio remained unchanged.
Second, the preservice teachers could take advantage of the greater precision of the technology seeing that for an 11º triangle, the slope ratio is not exactly 1/5, and for a line with a slope of 2/5, the angle it makes with the axis is not exactly 22º. Last, while this activity was focused on the creation and use of a tool to help each individual preservice teacher develop their own understanding of the mathematical relationships, we also recognized the potential for the preservice teachers to draw upon their TPACK and construct sketches that could help any user, not just themselves, develop mathematical understanding. The preservice teachers had used dynamic geometry software previously in the course and in other courses as part of their degree program. These sketches were submitted online and used in subsequent class meetings for further explorations and conversations.
From these submitted sketches, we looked at (a) the accuracy with which the sketches were built, (b) which aspects of their sketches that the preservice teachers chose to make variant and invariant, and (c) when a sketch was manipulated, whether it still represented the situation in the homework prompt that could be reasoned with.
Examining the Sketches
Sketches of 11º
To investigate a potential relationship between the 11º angle and a slope of 1/5, the preservice teachers were asked to create a sketch of an 11º angled line (see Figure 1).

From this sketch, it was expected that preservice teachers might notice what the slope of this line was by drawing in right triangles similar to the way they had been exploring during the in-class activity. However, when analyzing the sketches produced by the preservice teachers only 12 of the 31 sketches were constructed to specifically be (and remain) an 11º angle. (All names used in this paper are pseudonyms.)
For five of the preservice teachers, there appeared to be some confusion with the directions, as they instead created lines with a slope of 1/5. However, it was more common (in 14 of the 31 sketches), for lines not to be constructed to be 11º. Most frequently, the line was constructed through two points, a point through the origin, and an independent point (See Figure 2).

The independent point was placed so that the angle was approximately 11º, but upon moving the point, the line could change to have any angle. Because of this inexact angle measure, the slope of the line (and the right triangles off of the line) do not accurately represent the slope made when an exact 11º angle is used. This finding seemed to indicate an absence of technological content knowledge.
With paper-and-pencil constructions, an angle can be constructed by placing down a point and a line through that point and then using a protractor to find a point such that when the two points are connected, the two lines will have the given angle measure between them. In the technological environment, an important change occurs. The point cannot be placed manually with any guarantee of accuracy. Instead, the angle must be constructed to have the greater degree of accuracy. Preservice teachers who did this did not seem to understand how manually placing a point could affect the accuracy of their sketch and the impact it could have on further investigations in the sketch.
Additionally, only 15 of the 31 sketches actually displayed the 11º measure of the line produced in the sketch, letting them know what line was being investigated without having to search through other displays to find that information. Here, the preservice teachers did not take advantage of the labeling available in the dynamic geometry software environment, which can help display information about patterns of change or consistency. This point illuminates an opportunity to expand the preservice teachers’ technological pedagogical knowledge and how the display of information could affect what they, or other users, are able to glean from the sketches.
Through the activity in class, the preservice teachers had constructed right triangles off of the different lines they were investigating, comparing the ratio of the vertical and horizontal leg lengths of different triangles to determine the slope of the line. When constructing the 11º line sketches, right triangles were also produced in the sketches to compare the ratio of leg lengths. However, for eight of the 31 sketches, when the points of the sketch were dragged, these triangles did not remain right triangles (see Figure 3).

Although the triangles initially appeared to be right, the legs of the triangle were not constructed to remain at a right angle to each other. Thus, when manipulated, the ratio of leg lengths for these sketches did not accurately represent the slope of the line under investigation. Teachers may have an opportunity here to develop their technological pedagogical content knowledge. The technological manipulation brings with it the added requirement that every triangle remains a right triangle, not only the initial triangle. This knowledge is important for using this sketch as a tool to explore the patterns of right triangles off of a given line. Without the triangles remaining right, the preservice teachers would not have accurate information with which they could generalize a pattern.
Some of the preservice teachers did not take advantage of the dynamic nature of the software. Four of the preservice teachers created sketches in which slope triangles could not be manipulated. By fixing the points, the created slope triangles remained permanent and static and displayed lengths remained constant. For these sketches, the digital environment presented a medium for which more accurate lengths could be measured as compared to the ruler measurements obtained via pencil and paper in class. It is not clear whether this technological choice was done for any particular reason.
Although not explicitly required in the directions for creating the sketch, two additional observations were made when analyzing the sketches for the 11º angled line. The purpose of the in-class activity was to compare the angle measure of lines to their slopes using the ratio of leg lengths of right triangles to provide that ratio. In their created sketches, the majority of the preservice teachers had the side lengths of their triangles dynamically labeled (27 of 31), while only 10 of the 31 displayed the ratio of the leg lengths as either a ratio or as a decimal (which can make comparisons among different slopes easier).
It is not clear why this ratio was left off of so many sketches. Also, while not explicitly mentioned in the directions, it is interesting to note that for the 11º angle line, 22 of the preservice teachers created one triangle in their sketch, while eight of the preservice teachers created multiple triangles (one preservice teacher used no triangles).
One dynamically constructed triangle can be manipulated into numerous similar triangles, instead of including a separately constructed triangle for each new measurement. Here again, the activity affords opportunities to engage the preservice teachers in conversations to further develop their technological pedagogical content knowledge. Opportunities arise to discuss why the display of a dynamic slope ratio or decimal could be important for the generalization of patterns, or to discuss the advantages and disadvantages of multiple constructions versus a single construction and why they could make relationships more or less difficult to visualize. There are opportunities for teachers to understand in new ways technology can impact the mathematics that users have access to in explorations.
Sketches of 2/5 Slope
To investigate the angle measure made by a slope triangle with a ratio of 2/5, preservice teachers were first instructed to create sketches that contained the line y = (2/5)x, and create slope triangles off of these lines which would help them investigate the angle made, similar to investigations they had done in class (see Figure 4).
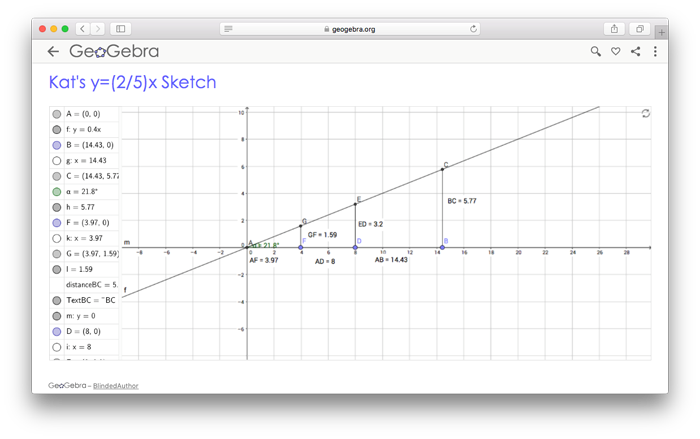
Twenty-six of 31 sketches contained a line of slope 2/5. For the seven sketches where this line was not created, similar to the 11º construction, two points were placed in the sketch (one at the origin and one independent) through which a line passed that approximated the line y = (2/5)x. The line was not exact, however, nor would it remain at a slope of 2/5 when points were dragged and manipulated. Again, there seemed to be some technological content knowledge that was not utilized in the creation of these sketches to help more accurately display these relationships.
Also, only 16 of the 31 sketches were labeled on the sketch that a line of slope 2/5 had been created. Nine sketches contained this information in a side display of all points and lines in the sketch, while this information was not displayed in eight of the sketches, providing opportunities to talk about technological pedagogical knowledge and how the display of information can help to provide an understanding of what is going on in a sketch.
Similar to the results of the 11º sketch, the right triangles produced in these diagrams did not often remain right triangles when manipulated. For eight of the 31 sketches, the legs of the triangles were not fixed to remain right triangles (see Figure 5). This error was problematic when the leg of the right triangle parallel to the x-axis did not remain parallel to the x-axis, affecting the angle measure of the line when measured. Technological pedagogical content knowledge may be further developed by discussing the difficulty in using an interactive sketch to investigate right triangles, but it does not feature triangles that always contain a right angle when manipulated.

Perhaps because the goal of this sketch was to investigate the angle measure of the line through slope triangles, the side lengths of the right triangles were only displayed in 19 of the 31 triangles. The angle was dynamically displayed in 27 of the 31 sketches, which showed how the manipulation of the slope triangles always featured a constant angle.
Last, while the majority of the preservice teachers created sketches that took advantage of the dynamic geometry software, four sketches produced did not allow points to be manipulated. Instead a static sketch was produced that displayed the given line, slope triangles, and angle. Like the static sketches for the 11º angle, this approach took advantage of the precision offered by the digital environment but not the dynamic opportunities.
Looking Across the Two Sketches
Throughout the sequence of activities, the preservice teachers explored the relationship between the angles of lines on the Cartesian plane and the slopes of those lines. For small angles, there appeared to be a linear relationship between the angle and the slope of the line, leading many preservice teachers to initially conjecture that the 11º and 22º angle and 1/5 slope and 2/5 slope pattern would continue linearly. However, these measures are not exact (the angles are measured to the nearest degree), and the slopes were the best estimates based on pencil-and-paper drawings. To help investigate a more precise pattern between these two variables, and continue exploring this relationship via slope triangles produced from the paper-and-pencil activities, the preservice teachers were tasked with creating two sketches of lines with an 11º angle and with a 2/5 slope that were dynamic and allowed manipulation of created slope triangles to explore the relationship.
The construction of these sketches involved an overlap of mathematical, pedagogical, and technological understanding. The sketches produced by the preservice teachers varied in quality and sometimes prevented desired patterns from being observed. One of the most fundamental challenges regards what features must remain constant and unvarying within the sketches produced. The preservice teachers were asked to construct sketches that had lines of 11º and a slope of 2/5, and to build dynamic slope triangles off of those lines. The purpose was to notice patterns in the ratio of the leg lengths or the angle the line made with the given slope.
In order to notice these patterns, the lines must be fixed at 11º or with a slope of 2/5. Without each feature being held constant, it becomes much more difficult to observe how the related measurements change or remain constant. In order to build sketches that follow these rules, the preservice teachers needed to understand not only how to create lines, but to create them so that they remain fixed based upon a desirable measure (angle or slope). Preservice teachers appeared to be better able to create a fixed line of slope 2/5 than a line of 11º.
Perhaps this comfort is due to familiarity with other standard graphing technologies that ask users to plot relationships as functions of x, as opposed to the graphing based on angles. This approach may be a feature that beginning teachers need further support in as they incorporate these kinds of features into their sketches.
A second challenge that occurred in multiple sketches was the way in which the right triangles were created from the given lines, which would not remain right angles if they were moved. The preservice teachers needed to think through what point or points they wanted to interact with and how to ensure that a right triangle would always result from manipulating the available points. If the point to be manipulated was located at the right angle, then two lines perpendicular to each other and parallel to the x and y axes can be constructed based on that single point.
However, if a point on the line where one of the legs of the triangle meets the hypotenuse is constructed first, this point does not determine the other two vertices of the right triangle. A second point (either on the line or at the right angle) must be created to determine the slope triangle. In this construction, two points determine the triangle and can be interacted with, instead of one in the previous construction.
Both of these issues can be addressed by giving the preservice teachers a chance to further develop their TPACK. These beginning teachers need additional experiences to think critically about how to use technology and build sketches and activities with technology in specific ways that are mathematically accurate and allow patterns to be noticed, explored, and even generalized based on experiences with the technology. They must more than expand their knowledge of mathematics content, learning, or technological familiarity separately. This knowledge is a unique kind that emerges when considering how to incorporate technology into the teaching and learning of mathematics effectively.
Dynamic Geometry Software and the Preparation of Mathematics Teachers
In some ways, dynamic geometry sketches are similar to static diagrams, in that they are visual representations of figures and relationships, seeming to be a replacement (Hughes et al., 2006). When produced in pencil and paper, or when a sketch is initially opened, the figures are static and unchanging. However, the dynamic nature of the software adds a layer of planning for preservice teachers beyond what they would think about when creating static sketches, that transforms their opportunities for learning.
With the software, the preservice teachers must consider what aspects of their diagram should be moveable and which ones should remain fixed. This consideration is unique when using dynamic technology environments and can be addressed by developing beginning teachers’ TPACK. Once the desired variant and invariant aspects are identified, the preservice teachers also have to think through how to make the remainder of their sketch and how the placement of points and lines might make subsequent figures dynamic or fixed and independent or dependent on other constructed pieces. Unique to dynamic geometric environments is that sketch creators must consider which mathematical relationships they want their sketch to help illustrate through manipulation.
The dynamic geometry environment can allow for the emphasis of several mathematical practices (National Governors Association Center for Best Practices, & Council of Chief State School Officers, 2010). Software of this kind can be used to help preservice teachers make conjectures and notice patterns. Multiple examples of a sketch (in this case, slope triangles of a line) can be redrawn in rapid succession, allowing users to see what changes and what is constant as points are moved and different triangles are considered.
Preservice teachers do not always take advantage of these benefits, however. Sketches are not always able to be manipulated, and teachers can rely on single fixed figures and their corresponding measurements. Additionally, although a single figure can be dragged to represent multiple figures, some preservice teachers included multiple triangles in their sketches that were not asked for in the directions. These fixed sketches and multiple examples are a common feature of paper-and-pencil diagrams, which are static by their very nature, and must have several iterations of a figure to notice what is constant in a figure and what can vary. Again, teachers need to have experiences where they can think about how aspects of dynamic geometry software can alter the demands of the diagram and how users interact with the sketch to notice mathematical relationships.
Additionally, the technological environment allows mathematics educators and beginning teachers the ability to retrace the building of a sketch. This technological ability allows the story of these diagrams (Sinclair et al., 2012) to be uncovered by reviewing a sequenced log of each step taken during the creation of a sketch, whereas this sequence remains hidden in static drawn diagrams.
These sketches can be compared for the different parent-child relationships used in the creation of the sketch, highlighting why certain features of the sketch vary, while others remain invariant. Two sketches that might appear to behave similarly can be constructed via different methods, highlighting the use of different pedagogical properties and allowing preservice teachers to see the logic used to build these sketches to highlight specific mathematical relationships.
Mathematics teacher educators who support beginning and preservice teachers’ learning about teaching mathematics with technology need to be aware of common issues and mistakes like those described here. The conversations we have with these teachers must include not only how to use particular pieces of technology, but also the strengths and limitations to using that technology to teach specific content, including how sketches should be constructed to highlight particular mathematical phenomena. Additionally, we can make explicit with these beginning teachers common errors or issues with using the technology that can prevent the recognition of patterns and relationships.
As these preservice teachers go out into the field and use technological tools with their own students, they need to be mindful that the ways in which they construct sketches to develop their own understanding of mathematics may need to be adapted for the diverse learners in their classrooms. Although they, as sketch creators, may understand the mechanics about how their sketch behaves, the students in their classrooms are not privy to that information. Thus, care needs to be taken when designing sketches so the mathematical patterns that users can see are accurate, relationships are variable or constant in intended ways, relevant information is displayed, and the sketch minimizes difficulties that could prevent exploration.
The knowledge to use technology effectively in the teaching and learning of mathematics involves the interactions of multiple domains (Mishra & Koehler, 2006). Teachers need to know what mathematical content to highlight, how to build sketches to illustrate the mathematics content, and how student interaction with the sketches might hide or highlight the mathematical content.
The question is then raised regarding when and where preservice teachers will learn about teaching mathematics with technology and who is responsible for teaching it. Is this learning the role of content courses for teachers, where the focus can be on the mathematics and how technology can be used with different content areas? Perhaps this learning occurs in methods courses, where the focus can center on how preservice teachers think about and make sense of mathematics and how they can investigate patterns with high-level tasks that include technology in transformational ways (Hughes et al., 2006).
Maybe some teacher preparation programs have specific courses in teaching and learning with technology, during which preservice teachers learn about multiple technological tools that can be used across different subject areas. A complex interaction occurs between mathematics, technology, and pedagogy as teachers attempt to use dynamic geometry software to help preservice teachers come to a rich understanding of mathematics content. In some ways, the knowledge required to use tools such as these is different than the knowledge as part of a regular content or methods course (Mishra & Koehler, 2006). If teachers are to take full advantage of the affordances that technology tools offer, then teacher preparation programs must specifically devote time to helping preservice and beginning teachers learn how to effectively design and implement technological experiences.
References
Brakoniecki, A., Glassmeyer, D., & Amador, J. (2016). Examining preservice teacher thinking about technology-based trigonometric explorations through a replacing, amplifying, and transforming framework. In M. B. Wood, E. E. Turner, M. Civil, & J. A. Eli (Eds.), Proceedings of the 38th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 1463–1470). Tucson, AZ: The University of Arizona.
Hughes, J., Thomas, R., & Scharber, C. (2006). Assessing technology integration: The RAT – Replacement, amplification, and transformation – framework (Vol. 2006, pp. 1616–1620). Paper presented at the Society for Information Technology & Teacher Education International Conference. Retrieved from www.editlib.org/p/22293
Mishra, P., & Koehler, M. J. (2006). Technological pedagogical content knowledge: A framework for teacher knowledge. Teachers College Record, 108(6), 1017–1054.
National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common core state standards for mathematics. Washington, DC: Authors.
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4–14.
Sinclair, N., Healy, L., & Sales, C. O. R. (2009). Time for telling stories: narrative thinking with dynamic geometry. ZDM, 41(4), 441–452. doi.org/10.1007/s11858-009-0180-x
Sinclair, N., Skelin, M., & Pimm, D. (2012). Developing essential understanding of geometry for teaching mathematics in grades 9-12. Reston, VA: National Council of Teachers of Mathematics.
Trocki, A. (2014). Evaluating and writing dynamic geometry tasks. The Mathematics Teacher, 107(9), 701–705. doi.org/10.5951/mathteacher.107.9.0701
![]()