One potential source of teacher professional growth is through collaborative efforts among teachers and outside organizations (Fullan, 1993). The success of these efforts has been closely linked to the professional development provided to the teachers engaged in the collaboration. Principles common to successful professional development include a targeted focus on instruction; instructional improvement comprising awareness, planning, implementation, and reflection; shared expertise; clear expectations; and collegiality, caring, and respect (Ball & Cohen, 1999; Elmore & Burney, 1999; House, 1994; Little, 2001). In successful collaborations, practicing teachers have the opportunity to work with diverse stakeholders (e.g., university faculty, educational researchers, and district level leadership) to explore subject matter content and various approaches to instruction (Lieberman & McLaughlin, 1992).
By engaging in well-planned collaborative efforts, teachers benefit from utilizing new curriculum materials and having the opportunity to engage in purposeful professional development, while the university faculty and educational researchers benefit from the chance to study how these new curriculum materials and professional support are used by teachers in their classroom settings. If professional development achieves an “inquiry stance on teaching,” teachers with varying degrees of professional experience can challenge their knowledge and practice, and as a result, they create high expectations for students’ learning and their own professional growth (Cochran-Smith & Lytle, 2001, p. 46).
This paper describes one such collaborative effort, entitled the SunBay Digital Mathematics Project. In this project faculty members from a public university’s college of education, educational researchers from an independent, nonprofit research institute, and district leaders from a large and diverse K-12 school district worked together to support middle school mathematics teachers’ classroom implementation of innovative curricular materials supported by professional development designed for sustainable change in practice. The curricular materials were designed to improve students’ learning of essential algebraic content identified by state and national standards (Florida Department of Education, 2012; National Council of Teachers of Mathematics, 2000; National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010).
We focus on important concepts in algebra because, as Kilpatrick (2009) emphasized, traditional approaches to instruction tend to foster deep misconceptions about the nature of algebra. For example, many students believe algebra is primarily “letters of the alphabet that are used, along with symbols for numbers, operations, and relations, to express relationships among known and unknown quantities” (p. 12). In addition, traditional teaching approaches often neglect the conceptual nature of algebra that can be fostered when a mathematics teacher presents concepts that connect algebraic, pictorial, verbal, graphical, and tabular representations in real world contexts (National Council of Teachers of Mathematics, 2001).
One resource for supporting practicing teachers’ efforts to engage their students in conceptually based mathematics is interactive digital technology (Kaput & Roschelle, 1997). Specifically, curricula that incorporates dynamic technology (e.g., SimCalc MathWorlds®) has been found to provide teachers with a compelling avenue to use motion phenomena to assist middle school students in learning “difficult math” by developing the sense that “every picture tells a story” (Nickerson, Nydam, & Bowers, 2000, p. 98). One such digital curriculum unit, created as part of a National Science Foundation project to replace a chapter in the classroom textbook, is entitled Managing the Soccer Team (SRI International, 2010).
Managing the Soccer Team Replacement Unit
In the 2-week curriculum replacement unit, Managing the Soccer Team, middle school mathematics teachers use SimCalc MathWorlds to engage students in a series of activities carefully designed to leverage student intuitions and support their conceptual understanding of complex algebraic concepts (Florida Department of Education, 2012; National Council of Teachers of Mathematics, 2000; National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010). Initially, tasks in Managing the Soccer Team require students to perform simple analyses of motion at a constant speed using multiple representations. These initial tasks emphasize straightforward graph and table reading (Vahey, Roy, & Fueyo, in press) or basic problems such as y = k x and
![]() .
.
However, as the unit unfolds, the students systematically follow a learning progression that culminates in more complex algebraic topics; more specifically, students investigate multirate functions and explore the meanings of positive, negative, and zero slope in motion contexts.
Finally, students investigate rate and proportionality in nonmotion contexts, such as saving money when purchasing team uniforms and predicting how much fuel vehicles would use in miles per gallon. Together, these tasks entail more complex proportional reasoning, requiring a functional approach or requiring reasoning across two or more representations (Vahey et al., in press).
Throughout the curriculum replacement unit the heuristic Predict, Check, and Explain provides a structure that allows the middle school students to gain a robust understanding of the various connected representations of rate and proportionality shown in Figure 1. By making predictions of motion contexts (e.g., who will win a race), the students’ existing knowledge is exposed.
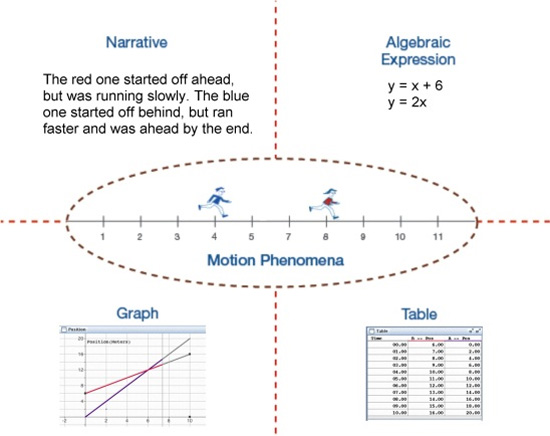 Figure 1. Multiple representations of motion phenomena.
Figure 1. Multiple representations of motion phenomena.
After making predictions about these motion phenomena, students run interactive computer simulations using SimCalc MathWorlds to check their predictions. Finally, teachers prompt their students to explain similarities and differences between their predictions and the computer simulations (Tatar et al., 2008). This use of computer simulations using SimCalc MathWorlds allows teachers to utilize technology as a tool to build student understanding of rate and proportionality concepts, a sharp contrast with traditional uses of technology in which technology is primarily used to either demonstrate ideas previously developed in the classroom or practice known procedures (Niess et al., 2009).
To investigate the viability of implementing curriculum replacement units that use dynamic technology on a large scale, the researchers conducted a randomized control study in seven diverse regions in Texas (Roschelle et al., 2010). Roschelle and colleagues reported that middle school teachers in the study were able to increase student achievement in the advanced mathematics covered using the replacement unit. More specifically, after comparing gain scores from pre-unit to postunit assessment, the seventh-grade students taught with the 2-week curriculum replacement unit and dynamic technology statistically outperformed students in the control group using the adopted textbook, regardless of demographics including gender, ethnicity, and poverty level (Roschelle et al., 2010; Vahey, Lara-Meloy, & Knudsen, 2009).
The work described in this paper builds on the research base described in Roschelle et al. (2010) and Vahey, Lara-Meloy, and Knudsen (2009). However, whereas the earlier study investigated implementation of a curriculum replacement unit by teachers across diverse regions in a large state, collaborators in the SunBay Digital Mathematics Project sought to research the classroom implementation of the 2-week curriculum replacement unit by middle school mathematics teachers in a large, diverse urban school district.
SunBay Digital Mathematics Project
During the SunBay Digital Mathematics Project, each of the collaborators provided complementary expertise to the project, shown in Table 1.
Table 1
SunBay Collaborators Contribution
Collaborator | Responsibilities |
| University Faculty Members |
|
| Educational Researchers |
|
| District Leaders |
|
Together the partners from these three organizations coordinated a series of inquiry-based professional development sessions as a means to ensure middle school teachers’ implementation of Managing the Soccer Team.
Research Focus
The data discussed in this paper highlight the university faculty members’ and educational researchers’ efforts to design an initial 3-day summer professional development followed by monthly professional development sessions aimed at engaging the teacher participants in learning about and planning for the implementation of Managing the Soccer Team. This unit served as replacement unit for a complete chapter in the seventh grade textbook adopted and used by teachers in the district.
Similar to the design process outlined in Simon (2000), data were analyzed on the team’s efforts to design and conduct each professional development session and then to reflect on the professional development process as a whole. These iterative cycles of planning, enactment, and reflection focused the team’s attention on the critical role that teachers’ knowledge plays when implementing key lessons in the replacement unit.
“Integrating technology is not about technology—it is primarily about content and effective instructional practices. Technology involves the tools with which we [teachers] deliver content and implement practices in better ways.” (Earle, 2002, p. 8) Following this reasoning, as part of our research, we sought to investigate the following question: “What type of knowledge is necessary for middle school teachers to implement a conceptually demanding curriculum replacement unit that incorporates dynamic technology?”
In order to explore this question we organized our professional development efforts around the intersection of three major domains of knowledge: content, pedagogy, and technology knowledge (TPACK), also known as technological pedagogical content knowledge (Mishra & Koehler 2006; Niess, 2005). The TPACK framework allowed the research team to emphasize the types of teacher knowledge needed to successfully utilize technology when teaching key algebraic concepts in the middle school curriculum. As a result, by using the framework we sought to ground teachers’ critical instructional decisions in their own evolving understanding of mathematics, pedagogy, and technology.
Teacher Participants
As stated, this study sought to explore middle school mathematics teachers’ implementation of curriculum replacement units that incorporate dynamic technology (e.g., SimCalc MathWorlds), as well as the professional development efforts needed to sustain classroom efforts aimed at students’ learning. All of the teachers taught in one of the top 25 largest school districts in the United States and one of the 10 largest in Florida (Sable, Plotts, & Mitchell, 2010).
As a part of recruitment efforts by the school district’s K-8 mathematics supervisor, mathematics teachers from 10 of the district’s 21 middle schools were invited to participate in the SunBay Digital Mathematics Project. Mathematics teachers from 7 of the 10 invited middle schools volunteered to participate in the project. From these 7 schools, 2 of the schools were classified high-poverty schools with greater than 50% of their students participating in the free or reduced lunch program. Initially, 15 mathematics teachers volunteered to participate in the pilot study. Ultimately, due to transfers between recruitment and the start of the project, 13 mathematics teachers from the 7 schools participated in the SunBay pilot and the professional development associated with the project. Each of the 13 teachers taught students in seventh-grade courses ranging from Regular Math through Algebra I Honors.
The 13 teacher participants had a variety of teaching experiences and educational backgrounds: the teachers’ classroom teaching experience ranged from 2 years to 24 years, and their diverse undergraduate preparation included degrees in finance, engineering, business administration, accounting, mathematics, history, health education, and special education. Many of the teachers had previous careers in the following fields: accounting, engineering, finance, marketing, and instructional technology.
Design Implementation
Records of key design decisions were collected to document the design and implementation of the monthly professional development sessions. Data included (a) notes from collaborative planning sessions between university faculty and nonprofit educational researchers; (b) field notes of professional development sessions written by university team members; and (c) teacher evaluations.
Additional sources of data produced by the participating teachers during professional development sessions were also collected for analysis; the data included: (a) teacher reflections; (b) teacher work samples; and (c) individual work assigned prior to professional development sessions. These products were continuously analyzed to reflect upon and plan for subsequent professional development sessions by the university faculty members and researchers from the nonprofit institute.
PowerPoint slides developed during the sessions were used as evidence to describe how we began to organize the teachers’ professional development around the TPACK framework. Field notes composed by the university team members were also used to help describe the teachers’ professional development participation and engagement with the digital unit as observed by each member. These field notes aided the team in making instructional decisions by allowing us to reflect on monthly sessions and plan for future professional development experiences accordingly.
Later in the project, the field notes and teacher artifacts were used to capture teachers’ reflections about their use of the digital curriculum materials and their comments about their own professional development experiences. The summary that follows describes how we used the TPACK framework to develop and organize the team’s professional development efforts.
Professional Development Details
Initial 3-Day Professional Development Workshop
Mathematics teachers must possess specialized knowledge of mathematics, pedagogy, and technology (Mishra & Koehler, 2006; Niess, 2005). We conjectured that teachers would be able to acquire this specialized knowledge by studying teaching materials, learning from colleagues, and doing mathematics. As such, the first emphasis of the SunBay Digital Mathematics Project was to provide the participating teachers with rich mathematical explorations emphasizing rate and proportionality by exposing them to curriculum materials that integrate technology for learning (Niess, 2005).
To this end, SunBay collaborators engaged the participating teachers in a 3-day professional development workshop prior to the academic school year in which the unit was taught. During these sessions the teachers explored the Managing the Soccer Team unit as mathematics learners. Workshop norms, including “Do the math” and “Make bold conjectures,” helped maintain the mathematical focus of the professional development and allowed the teacher participants to form their own mathematical connections about rate and proportionality.
Teachers were able to delve into rate and proportionality as identified by the state and national standards they are responsible to teach (Florida Department of Education, 2012; National Council of Teachers of Mathematics, 2000; National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010). In doing so, the teachers had the opportunity to develop their own mathematics knowledge prior to teaching the unit to middle school students.
Providing opportunities for teachers to “Do the Math” resulted in opportunities for teachers to broaden their own mathematics knowledge. For example, after running the SimCalc MathWorlds computer simulation shown in Figure 2, the teacher participants discussed their responses to the prompt, “Write a few sentences describing the motion of the bus and the van on the trip in the graph (Figure 2). Make sure to include what speeds the bus and the van traveled.”
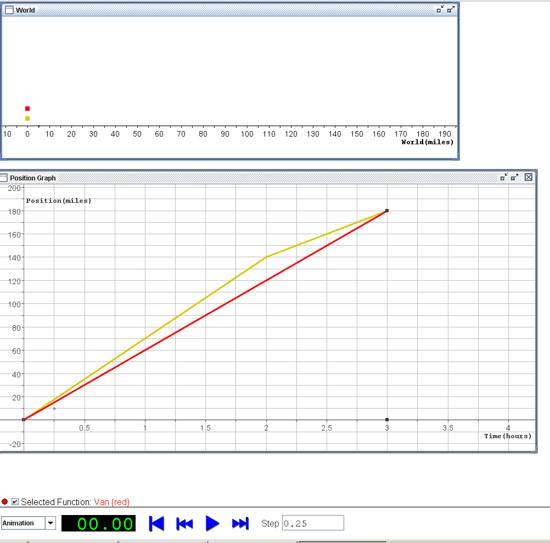 Figure 2. SimCalc MathWorlds-On the Road prior to the simulation being run.
Figure 2. SimCalc MathWorlds-On the Road prior to the simulation being run.
When running the computer simulation, the teachers were able to coordinate dynamically linked representations, including the “World” (located at the top of the screen shot) in which colored dots representing the bus and van travel at different rates of speed. This pictorial represented is connected dynamically to a corresponding “Position Graph” documenting the motion of both vehicles. After running the simulation, shown in Figure 3, all teachers recognized that the bus and van traveled at different speeds before arriving at their destination three hours later.
 Figure 3. SimCalc MathWorlds-On the Road after simulation has been run.
Figure 3. SimCalc MathWorlds-On the Road after simulation has been run.
That is, the teachers observed that the bus initially travels 140 miles during the first 2 hours of the trip and then travels 40 miles in the final hour, whereas the van travels at a constant speed for the whole 3-hour trip. All of the teachers agreed that the van traveled 60 miles per hour on the trip. However, two distinct ways of determining the average speed of the bus were presented.
In one line of reasoning, a teacher incorrectly conjectured that the distinct speeds of the bus should be added together and divided by two since the bus traveled at two distinct speeds. This results in an “average” speed of 55 miles per hour [(70 mph + 40 mph) ÷ 2]. Another teacher conjectured that since the bus traveled 180 miles in 3 hours it must have traveled an average of 60 miles per hour, regardless of the different speeds traveled. As the conversation progressed back and forth, other teachers provided justifications for both conjectures, and ultimately together the teachers correctly concluded that the bus averaged 60 miles per hour over the trip. By addressing the incorrect line of reasoning in whole group dialog, the teacher participants could address their own mathematical knowledge by exploring a possible misconception that may occur in their classrooms.
After the teachers experienced the unit as learners, we shifted the professional development focus so teachers could consider how best to teach the unit, using the norm of “Think about your classroom.” In this phase we developed the participants’ mathematical knowledge, while also emphasizing the classroom implementation of the replacement unit. The pedagogical focus included “the ways of representing and formulating the subject that make it comprehensible to others” (Shulman, 1986, p.9).
To accomplish this focus we provided the teachers with multiple chances to unpack potential teaching moves after engaging in the Predict, Check, and Explain heuristic during various activities in the replacement unit. That is, the teachers worked through key lessons (e.g., On the Road) by first focusing on their own thinking, and then relating it to their seventh-grade students. By doing so the teachers began anticipating the solution pathways that their students may use, and started to formalize how students’ predictions could shape whole class interactions and provide discussion opportunities in which students can articulate while teachers can evaluate their mathematical thinking.
Monthly Professional Development Sessions
Recognizing that using technology-mediated units that emphasize students’ verbal descriptions would be new to some of the teachers, the university faculty members and educational researchers decided that the teachers should continue to discuss pedagogical practices and strategies used to facilitate productive students’ thinking and mathematical discourse in the classroom beyond the timeframe of the initial 3-day workshop (Niess, 2005).
The research team decided that monthly professional development sessions could support these classroom interactions. Consequently, prior to the teachers’ implementation of the Managing the Soccer Team unit, portions of the monthly professional development sessions were devoted to teaching practices to support students justifying their thinking during classroom dialog, shown in Figure 4. By emphasizing the importance of the teachers’ reflections, we focused on how the teachers could use the information to make it a part of their pedagogical practice. Our goal was sustainable change in both teaching and learning—“explicitly connecting teacher and student learning” (Lieberman & Miller, 2001, p. ix).
Justifying Thinking
- Asking for Reasons for Answers
- Probing Student Responses
- Asking for Justifications for Incorrect and Correct Answers
- Asking for Multiple Explanations
- Reformulating Student Contributions
- Asking the Class to Evaluate
Figure 4. Research-based practices explored during professional development.
Interactions during one of the monthly sessions included four groups of three teachers discussing why it is important to implement these practices in their classrooms, in addition to how they would use the research-based strategies during a target lesson entitled On the Road, shown in Figure 5.
Target Lesson: On the Road
- Describe how you will use at least two of the research-based practices when teaching On the Road.
- Where in the lesson may Predict, Check, and Explain impact students’ learning?
- What advice would you give other teachers when teaching On the Road?
Figure 5. Implementation focus of research-based strategies.
One group of teachers concluded that they would require their students to justify correct and incorrect solutions. The teachers said they would ask their students to explain why and to continue to think about a problem by adding to and providing different solutions. The teachers also stated that they would reformulate students’ contributions by requesting that their students use mathematics vocabulary to explain their thinking, shown in Figure 6. This request would allow the teachers “more opportunities to question [students’] misconceptions.”
Responding to First Prompt of Figure 5:
Two Research Based Practices
- [We would ask students to provide] justification for correct and incorrect answers about the bus [by asking the following]
- Explain why?
- Does anyone want to add to that?
- Does anyone differ from that?
- [We would] reformulate [student] contributions [by stating]:
- Now let’s use math to explain vocab
Responding to Second Prompt of Figure 5:
[In questions] 3 & 4, Predict, Check, Explain [allows] more opportunities to question their [students’] misconceptions.
Responding to Third Prompt of Figure 5:
Don’t allow them [students] to watch the simulation until they make their predictions and stories.
Figure 6. Participating teachers’ responses.
When responding to the same prompts, another group of teachers stated that they would ask their students to justify predictions by asking “why they came up with them [predictions].” The teachers also stated that they would probe students’ responses when their students interpreted graphs during the lesson. Finally, as the previous group of teachers indicated, they would reformulate responses in order to “translate” students’ responses “into proper math language” (Figure 7).
Responding to First Prompt of Figure 5:
How we’ll use research-based practices:
- [Ask students] to justify predictions
- Why they came up with them [predictions]?
- Probe students’ responses [when] interpreting graphs
- Reformulate responses
- When students describe graphs, translate them into proper math language; i.e., slope
Responding to Third Prompt of Figure 5:
Advice for other teachers:
- Incorrect predictions are as valuable as “correct” ones
Figure 7. Another group of participating teachers’ responses.
The teachers’ responses document how core aspects of the professional development activities allowed the teachers to consider reflectively how they could use research-based methods to increase student learning of challenging mathematics.
As the project progressed, it became evident that the technology usage also needed to be a focus of monthly professional development sessions. We expected the participating teachers to be comfortable with the use of technology in the classroom, as they were recruited to be the first cohort to implement this replacement unit in the cooperating district; this was not the case. For instance, despite having a mobile cart of laptops available for individual student use during the unit, one teacher found that logistical aspects of computer use hindered effective technology integration into her classroom. The teacher was unable to create effective procedures for computer distribution, for students logging onto the computers, or for students to request necessary technical assistance. This teacher also indicated that the instructional unit would be easier to teach if the school’s technology person was in class when the students were using the laptops.
We also found that some of the participating teachers did not use the technology with the level of intensity they forecasted during the initial professional development. To aid teachers in more effectively using technology in their classrooms, portions of monthly professional development sessions were dedicated to using the technology by framing the technology usage in key lessons in the digital unit. We emphasized the pedagogical purpose (Figure 8) emphasizing how SimCalc MathWorlds helps develop the mathematics content in the lesson, Isabella Improves. We also prompted the teachers to describe the technology procedures they would use when teaching the lesson, in order to assist the teacher having difficulty with computer distribution.
Lesson Preparation: Isabella Improves
Overview
- What is the main mathematical concept constructed during the lesson?
- What additional mathematics concepts support the main concept?
- How will you use technology to develop the main concept?
- What prerequisite mathematics knowledge must students have before you teach this lesson?
- What procedures/materials must be in place to implement the lesson?
- Describe the setting in which you will be teaching the lesson.
Figure 8. Professional development slide highlighting technology foci.
Finally, during the last monthly session we engaged the participating teachers in dialog describing how technology changed their teaching of rate and proportionality. To do so, we asked the teachers to reflect on their implementation experience with their middle school students. After the teacher participants conversed in focus groups, two teachers synthesized their professional development experience in the following quotes:
I think that without that [PD], the program would not have been successful. [The PD] served as an introduction, and provided more extensive training. Normally we are just thrown in cold. [The SunBay team] provided us with overview and foundation. I think there was a lot of modeling to let us see alternative strategies for teaching Managing the Soccer Team. When you’ve taught for a while, you can get in a rut….It is nice to see best practices and current practices…sharing of ideas for groups and individuals….It gave us an alternate way of presenting the mathematics.
[The PD sessions] were good; I liked the fact that [the project team] seemed not only to be concerned about the field test, but opening us up to ideas and strategies that I had forgotten or never learned. I learned stuff about SimCalc [dynamic technology used in the Managing the Soccer Team replacement unit] but also something to be a better teacher.
Conclusion
Bringing together middle school teachers for monthly professional development sessions focused on mathematics instruction offered them the opportunity to access new ideas in a supportive community and provide meaningful action in schools and classrooms (Lieberman, 1995). By addressing the three types of interrelated TPACK knowledge during the professional development component of the SunBay Digital Mathematics Project, we provided regular opportunities for discussion and reflection about mathematics, pedagogy, and technology, in that order, for the participating teachers when teaching a digital curriculum.
Similar to previous research, these support structures allowed for the participating teachers to implement the digital unit in a way that they best saw fit (Roschelle et al., 2010; Tatar et al., 2008). For example during classroom implementation, we observed that the teachers varied in their instructional approach to the different activities. Some teachers had students work individually with their own computer, some in pairs or small groups sharing one computer, and some as a whole class where the teacher would drive the technology based on student responses. Regardless of the instructional approach, experiences during professional development allowed the participating middle school teachers to deepen their intertwined knowledge base of mathematics, pedagogy, and technology and lay the groundwork for using technology when teaching mathematics in the future.
Future Research
Collaborative relationships have been shown to be critical supports to the scale-up of innovative programs (Tatar et al., 2008). One of the most compelling is the example of the Boston Public Schools, a “district learning agenda grounded in teachers’ collaborative, school-based learning, and data outcomes for both students and adults in the district” (McLaughlin & Talbert, 2006, p. 123). As such, it is our intent to take what we have learned while providing engaging and collaborative professional development with the participating teachers of the SunBay Digital Mathematics Project and bring the project to scale.
We have learned the importance of changing teacher behavior and knowledge in professional development sessions by targeting instruction and instructional improvement comprising awareness, planning, implementation, and reflection through sharing expertise among the teachers and those conducting the professional development. As we expand our work to other schools in the district, we plan to investigate further the professional development structures needed to sustain these changes.
References
Ball, D., & Cohen, D. (1999). Developing practitioners: Toward a practice-based theory of professional education. In L. Darling-Hammond & G. Sykes (Eds.), Teaching as the learning profession: Handbook of policy and practice (pp. 3-32). San Francisco, CA: Jossey-Bass.
Cochran-Smith, M., & Lytle, S. (2001). Beyond certainty: Taking an inquiry stance on practice. In A. Lieberman & L. Miller (Eds.), Teachers caught in the action: Professional development that matters (pp. 45-58). New York, NY: Teachers College Press.
Earle, R. S. (2002). The integration of instructional technology into public education: Promises and challenges. Educational Technology, 42(1), 5-13.
Elmore R., & Burney, D. (1999). Staff development and instructional improvement: Community District 2, New York City. In L. Darling-Hammond & G. Sykes (Eds.), Teaching as the learning profession: Handbook of policy and practice (pp. 3-32). San Francisco, CA: Jossey-Bass.
Florida Department of Education. (2012). Next generation sunshine state standards: Mathematics (No. MA.7.A.1). Retrieved from http://floridastandards.org/Standards/PublicPreviewIdea209.aspx
Fullan, M. (1993). Change forces. Levittown, PA: The Falmer Press.
House, P. A. (1994). Empowering K-12 teachers for leadership: A districtwide strategy for change. In A. F. Coxford (Series Ed.) & D. B. Aichele (Vol. Ed.), Professional development for teachers of mathematics: 1994 Yearbook (pp. 214 -226). Reston, VA: National Council of Teachers of Mathematics.
Kaput, J. J., & Roschelle, J. (1997). Deepening the impact of technology beyond the assistance with traditional formalization in order to democratize access to ideas underlying calculus. In E. Pehkonen (Ed.), Proceedings of the 21st conference of the International Group for the Psychology of Mathematics Education (pp. 105-112). Lahti, Finland: University of Helsinki.
Kilpatrick, J. (2009). Algebra is symbolic. In S.L. Swars (Ed.), Proceedings of the 31st annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, (pp. 11-20). Atlanta, GA: Georgia State University.
Lieberman, A. (1995). Practices that support teacher development. Phi Delta Kappan, 76(8), 591-596.
Lieberman, A., & McLaughlin, M. W. (1992). Networks for educational change: Powerful and problematic. Phi Delta Kappan, 73(9), 673-677.
Lieberman, A., & Miller, L. (Eds.). (2001). Teachers caught in the action: Professional development that matters. New York, NY: Teachers College Press.
Little, J. (2001). Professional development in pursuit of school reform. In A. Lieberman & L. Miller (Eds.), Teachers caught in the action: Professional development that matters (pp. 23-44). New York, NY: Teachers College Press.
McLaughlin, M.W., & Talbert, J. (2006). Building school-based teacher learning communities: Professional strategies to improve student achievement. New York, NY: Teachers College Press.
Mishra, P., & Koehler, M. J. (2006). Technological pedagogical content knowledge: A framework of teacher knowledge. Teachers College Record, 108(6), 1017-1054.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (2001). Navigating through algebra in grades 6-8. Reston, VA: Author.
National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common core state standards for mathematics. Washington, DC: Authors.
Nickerson, S. D., Nydam, C., & Bowers, J. S. (2000). Linking algebraic concepts and context: Every picture tells a story. Mathematics Teaching in the Middle School, 6(2), 92-98.
Niess, M. L. (2005). Preparing teachers to teach science and mathematics with technology: Developing a technology pedagogical content knowledge. Teaching and Teacher Education, 21(5), 509-523.
Niess, M. L., Ronau, R. N., Shafer, K. G., Driskell, S. O., Harper S. R., Johnston, C., … Kersaint, G. (2009). Mathematics teacher TPACK standards and development model. Contemporary Issues in Technology and Teacher Education [Online serial], 9(1). Retrieved from https://citejournal.org/vol9/iss1/mathematics/article1.cfm
Roschelle, J., Shechtman, N., Tatar, D., Hegedus, S., Hopkins, B., Empson, S., …Gallagher, L. (2010). Integration of technology, curriculum, and professional development for advancing middle school mathematics: Three large-scale studies. American Educational Research Journal, 47(4), 833-878.
Sable, J., Plotts, C., & Mitchell, L. (2010). Characteristics of the 100 largest public elementary and secondary school districts in the United States: 2008–09 (NCES 2011-301). U.S. Department of Education, National Center for Education Statistics. Washington, DC: U.S. Government Printing Office.
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4-14.
Simon, M. A. (2000). Research on the development of mathematics teachers: The teacher development experiment. In A. E. Kelly & R. A. Lesh (Eds.), Handbook of research design in mathematics and science education (pp. 335-359). Mahwah, NJ: Lawrence Earlbaum Associates, Publishers.
SRI International (2010). Design and development of curriculum units and professional development. Menlo Park, CA: SRI International.
Tatar, D., Roschelle, J., Knudsen, J., Shechtman, N., Kaput, J., & Hopkins, B. (2008). Scaling up innovative technology-based mathematics. Journal of Learning Sciences, 17(2), 248-286.
Vahey, P., Lara-Meloy, T., & Knudsen, J. (2009). Meeting the needs of diverse student populations: Findings from the SimCalc project. In S.L. Swars, D.W. Stinson, & S. Lemons-Smith (Eds.), Proceedings of the 31st annual meeting of the North American chapter of the International Group for the Psychology of Mathematics Education (pp. 416-424). Atlanta, GA: Georgia State University.
Vahey, P., Roy, G., & Fueyo, V. (in press). Sustainable use of dynamic representational environments: Toward a district-wide adoption of SimCalc-based materials. In S. Hegedus & J. Roschelle (Eds.), Democratizing access to important mathematics through dynamic representations: Contributions and visions from the SimCalc research program. New York, NY: Springer.
Author Notes
The Managing the Soccer Team curriculum unit was written and adapted during work supported by the National Science Foundation under Grant No. 0437861, as well as grants from the Helios Foundation, Pinellas Education Foundation, and the Pinellas County Schools. Current SunBay Digital Math work is supported by an EDUCAUSE grant through the Next Generation Learning Challenges. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation, EDUCAUSE, Pinellas Education Foundation, the Helios Foundation, or the Pinellas County Schools. The authors would like to thank the teachers in Texas and Florida who were willing to use our materials and provide feedback to the team. The authors would also like to thank the teams at the University of South Florida St. Petersburg and SRI International for their contributions to the project.
George J. Roy
University of South Florida St. Petersburg
Email: [email protected]
Charles Vanover
University of South Florida St. Petersburg
Email: [email protected]
Vivian Fueyo
University of South Florida St. Petersburg
Email: [email protected]
Phillip Vahey
SRI International
Email: [email protected]
![]()