In the USA, demand for high quality professional development (PD) for K-12 teachers has been highlighted by adaptation of Common Core State Standards (CCSS) for Mathematics (National Governors Association and the Council of Chief State School Officers, 2010). Research has identified key features of effective PD (e.g., Darling-Hammond et al., 2017; Desimone, 2009) and has widely documented that lesson study (LS) demonstrates these features (Huang & Shimizu, 2016; Lewis & Perry, 2017).
Research has also documented that LS yields positive effects on teacher learning, student learning, and curriculum reforms (Gersten et al., 2014; Huang & Shimizu, 2016; Lewis & Perry, 2017; Xu & Pedder, 2014). Yet, several obstacles in the US educational system have prevented LS from being implemented sustainably at scale. Lack of accommodating teaching schedules and qualified LS facilitators are the two major obstacles (Akiba & Wilkinson, 2016; Cravens & Drake, 2017).
Some studies have explored and showed promise with alternative approaches such as using self-videotaped research lessons or cartoon animation to help teachers reflect upon and improve their practice, rather than watching and reflecting on a live research lesson as a typical LS does (Beisiegel et al., 2017; Borko et al., 2015; Skultety et al., 2017). In addition, using various digital technologies and online conferencing systems for teacher PD have shown the potential to remove physical obstacles to teacher collaboration (Choppin et al., 2020; Community for Advancing Discovery Research in Education [CADRE], 2017).
The question has been underexplored, however, of whether these various digital technologies could be utilized together to assist in conducting LS so as to remove scheduling obstacles, while retaining the benefits of LS. To this end, this study was designed to explore how TALS could be implemented effectively by using the Swivl video collaboration system and the Zoom video- conferencing system to allow the LS to be embedded into normal teaching schedules, thus eliminating the scheduling obstacle.
Literature Review
The relevant literature incudes two sections. After synthesis of the features of LS and its effects, studies on addressing the challenges of adaption of LS at scale are summarized.
Features of Effective Lesson Study and Its Effects
LS is a teacher-oriented, student-focused, job-embedded, collaborative teacher PD approach (Lewis, 2016; Murata, 2011). A typical Japanese LS includes four major steps: (a) Study – Setting goals for student learning; (b) Plan – Collaboratively planning a research lesson to address identified goals; (c) Teach – One team member teaching a lesson while the others observe and record observations; and (d) Reflect – Reflecting and revising the research lesson and writing a report (Lewis, 2016).
Originating in Asia, LS has spread worldwide (Huang et al., 2019b). Variations of LS (Huang & Shimizu, 2016) include Chinese LS (Huang et al., 2017), HK/Sweden LS (a combination of design-based study and Japanese LS; Pang & Marton, 2003), and UK- research LS (a combination of action research and Japanese LS; Dudley, 2014). Yet, having repeated teaching of one research lesson to different groups of students and involvement of knowledgeable others (Takahashi & McDougal, 2016) are arguably crucial for ensuring the quality of a LS (Huang et al., 2018; Seleznyov, 2018).
Research has identified key features of effective PD to include (a) alignment with shared goals and assessment; (b) a focus on core content and modeling of teaching strategies for the content; (c) inclusion of opportunities for active learning; (d) provision of opportunities for collaboration among teachers; and (e) inclusion of embedded follow-up and continuous feedback (Darling-Hammond et al., 2017; Desimone, 2009).
Research has also documented that LS demonstrates these features of effective PD (Huang et al., 2019b; Lewis, 2016; Lewis et al., 2009). Specifically, in the study and plan phases, teachers collaboratively identify and plan for addressing their goals related to better teaching core content through the LS. The research lessons themselves aim to model teaching strategies for this content. All teachers in the LS are actively engaged in learning through LS by planning, reviewing, debriefing, and revising lessons, and additionally, some of the teachers teach the lesson. The entire LS process is collaborative, and multiple cycles of LS allow for follow up and continuous feedback, which can be sustained through additional lesson studies throughout the school year.
With the popularity of LS as teacher PD internationally, many studies have documented the effects of LS, which include improving teaching and student learning, promoting teacher learning, implementing new curriculum, and developing a teacher professional learning community (e.g., Huang & Shimizu, 2016; Willems & Van den Bossche, 2019; Xu & Pedder, 2014).
Addressing the Challenges of Adapting LS at Scale
In contrast to the pervasive use of LS in China and Japan, LS has been implemented only sporadically in the US. A few studies have explored the implementation of LS district wide because of funded projects and have identified several factors necessary for scaling up LS. These factors include ensuring school ownership and leadership in organizing and facilitating LS and embedding LS into school organizational structures and routines (Akiba & Wilkinson, 2016; Takahashi & McDougal, 2016). However, the lack of accommodating teaching schedules and the lack of qualified LS facilitators continue to be two major obstacles (Akiba & Wilkinson, 2016; Cravens & Drake, 2017) to scaling up LS.
Researchers have attempted to address these barriers through various approaches. For example, to address the lack of knowledgeable others through a longitudinal and large-scale study Lewis and Perry (2017) found that LS supported by research-based mathematics resource kits could help teachers increase their knowledge for teaching the specific content and improve students’ learning outcomes.
Other researchers have explored developing teacher leaders who can facilitate teachers’ job-embedded PD (Borko et al., 2015; Jacobs et al., 2017). To address difficulties in scheduling live-class observations during LS, some studies explored alternative approaches. For example, researchers explored how technology (self-videotaped research lessons, or animation) helped teachers to reflect and modify lessons during an iterative process of examining lessons (Beisiegel et al., 2017; Borko et al., 2015; Skultety et al., 2017). Researchers have widely documented that teachers viewing their own or their peers’ videos, facilitated by trained teacher leaders, helped teachers to deeply reflect on their teaching (Beisiegel et al., 2017; Borko et al., 2014; van Es et al., 2014).
Many research studies have examined how teachers could develop their thinking and noticing, professional vision, and consequently, their teaching practice through analyzing videos guided by deliberate facilitating frameworks (Borko et al., 2011; Sherin & Han, 2004; van Es et al., 2014). Moreover, online teacher PD systems, as well as blended teacher PD systems involving the integration of onsite and remote components, have shown the potential to overcome the obstacle of difficulty in scheduling times for collaboration and to deepen participants’ reflection on their videos (CADRE, 2017; Choppin et al., 2020).
An Integrative Approach to Addressing the Challenge: Construct of TALS
Building on existing research findings and the researchers’ multiple years of LS experience (Huang et al., 2019a), incorporating effective features of traditional LS and making use of advantages of technologies, a technology-assisted lesson study (TALS) model was created as shown in Figure 1 to address the physical/time constraint obstacles created by the requirement of observing lessons and planning/debriefing in person.
Figure 1 The Process of TALS
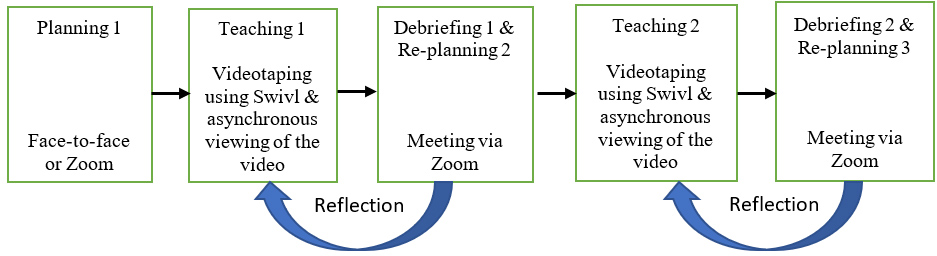
Two key components of a traditional LS, observation of live classes and facilitation of postlesson discussion were substantially restructured using technology. Key features of TALS include (a) all lesson planning meetings and postlesson debriefs are carried out during routine planning or professional learning community (PLC) periods or after school, as opposed to teachers missing class to debrief immediately following the teaching of the research lesson, and are facilitated by the online video-conferencing system Zoom when needed; (b) research lessons are self-video-taped using Swivl and uploaded to the Swivl cloud, as opposed to the LS team observing lessons in person; and (c) TALS team members asynchronously review the videos (with prompt questions created by the facilitator, supported by the research team) before postlesson debriefs.
Swivl is an intelligent technological assistant robot that has the capability of gathering high-quality audio and video from multiple groups within a classroom. The teacher wears a marker (with built-in microphone), which the Swivl robot tracks. Prior to a class, the teacher opens the Swivl application on an iPad (or phone), sets the iPad into a groove on the Swivl robot, connects the iPad and robot with a cable provided, and turns on the robot and the marker. Then the Swivl robot tracks the teacher by rotating the iPad horizontally and vertically, capturing the whole-class activities.
Additionally, the Swivl system has the ability to collect videos from up to four additional iPads (or phones or laptops) simultaneously, which allows small-group activity to be recorded. Before class, the teacher positions the iPads for small group activity and opens the Swivl+Student app on each iPad, which then prompts the teacher to enter a personal identification number, thus allowing the five videos to be associated with each other and synced.
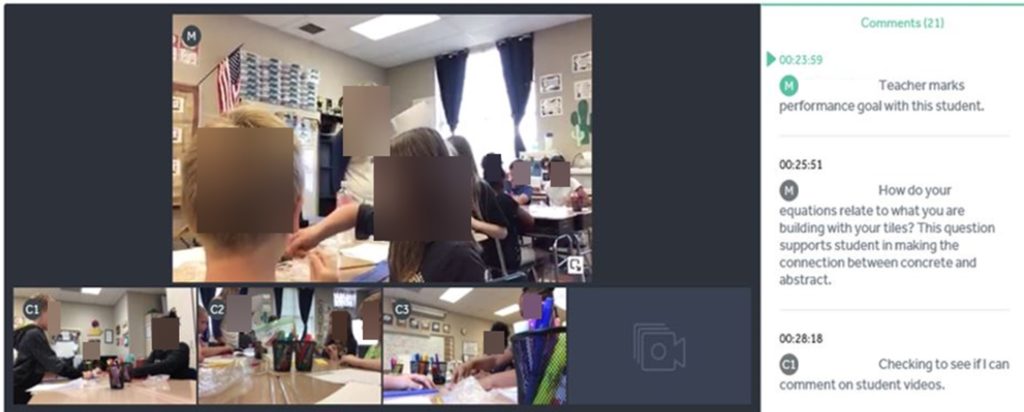
When video collection ceases, the technology provides opportunity for annotation of the videos, allowing for comments and reflection questions to be added prior to viewing. Swivl creates one integrated video file with up to five video windows (containing the video of the teacher and up to four student groups) and uploads the file to the Swivl cloud, producing a link for access.
Figure 2 shows a screenshot from a sample integrated video file (with teacher video M and three student group videos C1, C2, C3) which has been annotated with questions and comments. The viewers can click any video to play that video. When the viewer clicks an annotated comment or question on the right side, the video will be tracked back to the time associated with the annotation and played.
Figure 2 The Integrated Video With Annotated Questions and Comments
The Zoom video-conferencing system platform can incorporate audio and video feeds of multiple participants and includes features such as chats, screen sharing, breakout rooms, and video recording of the meeting. TALS team members may then participate in planning meetings and debriefing sessions from remote locations, if needed – a feature especially helpful for team members whose place of work is typically not the school in which the lesson study is conducted (mathematics specialist, university researchers, etc.).
This exploratory study was designed to explore the feasibility and effects of the TALS model. The study addressed the following research questions:
- Does TALS promote participating teachers’ learning as indicated in traditional LS?
- What are the participating teachers’ and specialist’s perceptions of the usefulness and effects of TALS?
Theoretical Framework
Teacher Collaborative Learning and Community of Practice
Due to the nature of teacher collaborative learning, the school of socialcultural, situated perspective including Cultural-Historical Activity Theory (Engeström, 2001) and community of practice (Wenger, 1998) has been widely used to examine teacher learning in collaborative groups (Borko & Potari, 2020; Jaworski & Huang, 2014). The International Congress on Mathematics Education survey on mathematics teacher collaboration (Robutti et al., 2016) indicated that 80% of 85 papers reviewed employed the theoretical framework of community of practice (CoP; Lave & Wenger, 1991; Wenger, 1998) or community of inquiry (Jaworski, 2006).
To capture teachers’ learning through TALS, this study adopted the perspective of CoP with the enrichment of the concept of community of inquiry. According to Wenger (1998), learning occurs through collaboration with other members of the community who have a shared interest or common concern for something they would like to improve. Wenger defined a CoP as a group whose members are mutually engaged in an activity (e.g., coplanning, watching, and evaluating lessons), held together by a joint enterprise (e.g., addressing the goals of student learning set by a TALS group), and have a shared repertoire of customs for practice (e.g., norm of debriefing, routines of TALS, and shared views of an effective lesson).
Within a CoP, participants negotiate meaning through dual processes of participation and reification. Participation describes the active, experiential, and social process of taking part and sharing in communities (e.g., planning, teaching and evaluating the research lesson), whereas the complementary process of reification involves “giving form to our experience by producing objects that congeal this experience into ‘thingness’” (Wenger, 1998, p. 58; e.g., lesson plans, videotaped lessons, and student learning artifacts), which “become points of reference for sense making.”
Wenger (1998) further argued that the creation of learning communities “depends on a dynamic combination of engagement, imagination and alignment to make this interplay between the local and the global an engine of new learning” (p. 228). Engagement refers to doing things together, talking, and producing artifacts. Imagination includes reflecting, constructing an image of the practice and its members, and seeing self as one of them. Alignment means following directions, aligning self with expectations/standards, and coordinating actions toward a common goal. Thus, in mathematics learning and teaching, participants engage in their practice alongside their peers, use imagination in interpreting their practice, and align themselves with established norms and values.
Wenger et al. (2002) further reported on seven principles for cultivating communities of practice. Some are closely related to LS, such as opening a dialogue between inside and outside perspectives about the community (e.g., knowledgeable others and teachers), inviting different levels of participation (e.g., novice and experienced teachers), developing public and private spaces for members to interact with each other (e.g., teachers’ informal conversations and lesson planning and debriefing meetings), and creating a rhythm for the community (e.g., collaborative lesson planning and norms of debriefing meetings).
Jaworski (2006) developed the concept of community of inquiry (CoI) based on CoP and Wells’ (1999) perspective of dialogic inquiry: “a willingness to wonder, to ask questions, and to seek to make answers to them” (p. 122). Within a CoI, inquiry becomes a way of being or a professional stance, and participants collaboratively learn together and support each other in developing new forms of practice. Thus, teachers taking on an inquiry stance “engage with critical alignment (CA): they look critically at what they are doing and how they are doing it while engaging in practice. The critical nature of inquiry leads to possibilities for development in practice” (Jaworski & Huang, 2014, p. 178). Thus, in this study, a TALS group formed a CoI because the group had explored ways of implementing CCSS math-oriented lessons through critical inquiry.
Teacher Learning Through Lesson Study From the Perspective of CoI
The abstract nature of Wenger’s conceptualization of community and learning (Cobb et al., 2009) makes it powerful yet also creates an analytical challenge: how to productively make sense of learning inside a teacher CoP (Bannister, 2018). Bannister (2015) theorized teacher learning in a CoP using conceptual tools from frame analysis, which refers to the interactive, productive process of meaning-making in a group (Snow & Benford 1988). Through the frame, the teachers’ collective attentions (discourses) in a group are organized into three framings: diagnosing (i.e., identification of a problem), prognosing (i.e., a proposed solution to the diagnosed problem), and motivating (i.e., a call to arms or rationale). Using the frame analysis, researchers can track any shifts in participation and reification patterns within a community over time (Bannister, 2015; Horn, 2007) “based on what teachers found problematic, what teachers proposed as solutions, and what teachers said to garner support for their ideas” (Bannister, 2018, p.135).
Within a TALS CoI, beyond the three framings, the enactment of the proposed solution and reflection on the enactment are the key components. To theorize teacher learning from CoI (Jaworski, 2006; Wenger, 1998), this study developed a model by integrating the construct of CoI and cycle of lesson study as shown in Figure 3.
Figure 3 Connections Between Lesson Study and Community of Inquiry (Jaworski, 2006)
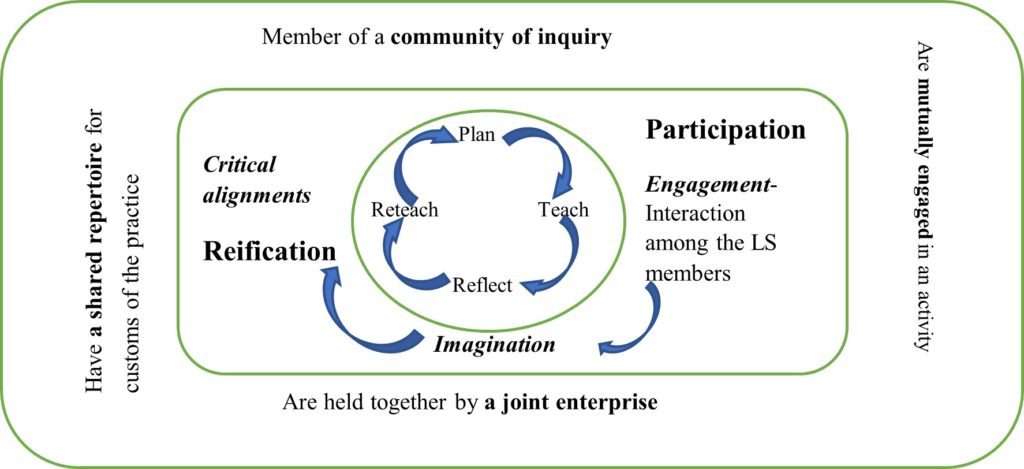
Within the context of TALS, a CoI typically consists of practicing teachers and knowledgeable others (mathematics specialists and researchers) mutually engaged in developing the research lesson, held together with the joint enterprise of achieving learning goals of the research lesson, and having a repertoire of conducting TALS (norms and procedures). In the CoI, setting goals of TALS is crucial: how to implement reform-oriented teaching in the classroom (National Council of Teachers of Mathematics [NCTM], 2014) from an inquiry stance.
By being involved in TALS and interacting with knowledgeable others, participating teachers have many opportunities to encounter innovative ideas from different perspectives that may find their way to their practice. Through the cycle of TALS, the participants engage in the joint enterprise through collaborative planning and enacting lessons, image the research-based effective teaching through evaluating the research lesson and revising the lesson plan, and make critical alignment with the imagination through reteaching and reflecting.
The final enacted research lesson reifies the critical alignments (Figure 3). Thus, we examined how to make critical alignments (CAs) of the development of the research lesson as key indications of teachers’ learning through TALS. In addition, an insider’s perspective from participating teachers and the district mathematics specialist further triangulated teachers’ learning through TALS. Thus, in this study, teacher learning through the lesson study process of planning, teaching, reflecting, reteaching, and reflecting was analyzed in terms of engagement, imagination, and critical alignment as illustrated in Table 1.
Table 1 Participation Patterns and Phases of Lesson Study
| Participant Patterns and Phases | Major Activities |
|---|---|
| Engagement (planning and teaching research lesson) | Collaboratively studying materials, setting goals, planning, and enacting research lessons |
| Imagination (evaluation and revision of research lesson) | Collaboratively evaluating research lesson and revising lesson plan in line with the frame of research-based effective teaching |
| Critical alignment (reteaching/ reflecting/revising research lesson) | Reifying research-based effective teaching through critically investigating what works and what does not work by reteaching and reflecting |
Methodology
The Lesson Study Group
The TALS took place in an urban school system in a midsize city in the southeastern US. The TALS group included two third-grade teachers (“Ms. Brown” and “Ms. Green”) from a typical elementary school, who participated on a voluntary basis; a mathematics specialist (“Ms. Haden”) from the school system; and three researchers (“Dr. Rose,” “Dr. Johns,” and “Dr. Long”) from a large public university in the city. Ms. Brown and Ms. Green are certified to teach grades preK-3 and had 5-12 years teaching experience at the time of the study. Dr. Rose, Dr. Johns, and Dr. Long are experienced in teaching preservice teachers and conducting PD for K-12 teachers. Ms. Haden is a veteran K-3 teacher and former adjunct professor at the university.
Ms. Haden, Dr. Rose, Dr. Johns, and Dr. Long are experienced in leading traditional LS; over the past 3 years they did such as part of a state-funded teacher PD project for K-8 teachers in the school system (Huang et al., 2019b). Ms. Haden led this TALS by facilitating lesson planning sessions, setting technologies for recording lessons, preparing embedded reflection questions for reviewing videos, and facilitating debriefing. Dr. Rose, Dr. Johns, and Dr. Long oversaw TALS activities, monitored the technology, and assisted with lesson planning meetings and facilitating debriefs.
The Goals of the Research Lesson
The school system has made great effort to implement state standards that are an adaption of CCSS (National Governors Association and the Council of Chief State School Officers, 2010) and to prepare their teachers to teach in a reform-oriented way (NCTM, 2014) through various PD programs. One of the attempts was a state-funded 3-year (2016-2018) mathematics and science partnership program led by the first three authors of this paper, aimed at deepening understanding of mathematics numeracy and implementing reform-oriented mathematics teaching of K-6 teachers (Huang et al., 2019b).
In line with this backdrop of curriculum and teaching reform, the research lesson developed and taught in this TALS was designed to help students understand the area model of multiplication and the commutative property of multiplication and to be able to relate area of rectangles to multiplication and addition (3. MD. C7., CCSS). At the same time, the lesson was intended to target several mathematical practices (National Governors Association and the Council of Chief State School Officers, 2010), such as Math Practice (MP) 1 – Make sense of problems and persevere in solving them; MP6 – Attend to precision; and MP7 – Look for and make use of structure.
The school system had promoted a teaching model which began with a number talk. A number talk is a short classroom routine involving a discussion among a teacher and students about how to solve a particular problem mentally, without paper and pencil. The goals of a number talk often include reviewing relevant skills and laying the foundation for introducing the main topic of the lesson (see page 16 of Parrish (2014) for an example). After the number talk, the teaching model involves exploration of high cognitive demanding tasks in groups (peer and pair sharing in groups), and then orchestration of student solutions in a whole classroom setting (Smith & Stein, 2018). The school system has also emphasized teaching through solving problems.
Process of TALS
To (a) set the goals of the TALS and (b) develop an initial plan of the lesson, TALS group members met during their normal common planning period in the school. Another purpose of this meeting was for the specialist to introduce the researchers and teachers and to build personal connection and trust among all team members. This initial meeting was facilitated by Ms. Haden and assisted by Drs. Rose, Johns, and Long (first three authors).
Ms. Haden helped the teachers develop a detailed lesson plan based on a local lesson plan template. Ms. Brown first taught the research lesson (RL1). During the lesson, Dr. Rose took notes focusing on the major events of classroom teaching with a focus on student learning, while Dr. Long took notes focusing on the use of the technologies (i.e., whether the technology captured what was intended or whether it could be better positioned, did the technology seem to be distracting the students, etc.) (During the lesson Ms. Haden assisted the students who were not video recorded because of lack of permissions). After the class, Ms. Haden annotated the videos by inserting comments and by posing reflection questions and then uploaded the integrated video to the Swivl cloud and sent a link to all members of the team so that they could access the video.
Each TALS member reviewed the videos (individually, on their own time) before the debriefing session, which was held during the teachers’ common planning period at school in the following day. It happened not to be inconvenient in that particular case for all to meet to debrief face to face; otherwise the debriefing session would have been held via Zoom.
The first debriefing meeting (DB1) was videotaped for research purposes. In the debriefing meeting Ms. Haden first set the norm of debriefing (focusing on the lesson and on student learning based on analyzing the videos, rather than critiquing the teachers). Then each member of the TALS team shared their perceptions of the strengths of the lesson (in order of enacting teacher, other teacher, specialist, and researchers). Next, the group discussed how the lesson could be improved in the next teaching. Finally, Ms. Haden summarized the major changes needed based on the discussion.
A revised lesson plan was made by Ms. Haden and the teachers. Based on the revised plan, Ms. Green taught the lesson in her class (RL2). Similarly, the lesson was videotaped using Swivl (and three IPads) and then annotated and uploaded by Ms. Haden for others to review. The second debrief (DB2) was conducted through Zoom and recorded following the same norms and procedures of the first debriefing (DB1). Finally, Ms. Haden revised the lesson plan again based on the second debrief and shared with the TALS group.
Data Collection
Multiple data sets surrounding the TALS were collected. These include the following:
- D1: Lesson plans for the two enacted lessons and the finalized lesson plan;
- D2: Videos of each enacted lesson (using Swivl and iPads);
- D3: Video recordings from the two debriefing meetings (the first debrief was recorded by an IPad; the second by the Zoom system);
- D4: Associated student learning artifacts such as completed worksheets in classes.
In addition, after completion of the entire TALS process, the two participating teachers were interviewed using a semistructured interview protocol (D5, see Appendix A). Interviews were designed to elicit teachers’ perceptions of the research lessons (strengths and weakness), benefits from TALS, and strengths and constraints of implementing TALS schoolwide. The specialist was also interviewed using a semistructured protocol (D6, see Appendix B) to elicit her perception of the effectiveness of TALS, strengths and weakness of using TALS in comparison with traditional LS, and the feasibility of using TALS at the district level.
The teacher interviews were conducted face to face by a graduate research assistant, and the specialist interview was conducted by the second author. Each interview lasted around 40 minutes and was audio recorded. Observation notes related to the use of technologies were also collected from the researchers.
Data Analysis
All collected audio and video data were transcribed by a research assistant. The data sources used for analysis to address each research questions are shown in Table 2.
Table 2 Research Questions and Corresponding Data Sources
| Research Question | Data Sources |
|---|---|
| 1. Does TALS promote participating teachers’ learning as indicated in traditional LS? | D1 (lesson plans of RL1 and RL2) D2 (videos of RL1 and RL2) D3 (transcripts of debriefing sessions 1 and 2) D4 (student artifacts) D5 (transcript of teacher interview) |
| 2. What are the participating teachers’ and specialist’s perceptions of the usefulness and effects of TALS? | D5 (transcript of teacher interview) D6 (transcript of specialist interview) |
Analysis of the data included three major steps. Using lesson plans and transcripts of the research lessons (D1 and D2) and student learning artifacts (D4), the first step focused on identifying and validating critical alignments through identifying salient and significant improvements from RL1 to RL2. The first author carefully read the transcripts of RL1 and RL2 line by line and consulted the original videos (D2) or lesson plans (D1), when needed, to make sure of understanding the lessons precisely. Then, a table was made to juxtapose the brief description of the two RLs in terms of the three phases of the lessons: (a) exploration of the number talk, (b) implementing a contextual task (designing a rug) in groups (pair-share in group), and (c) orchestrating sharing of student solutions in whole class.
Through comparison of each phase of RL1 with the corresponding phase of RL2, three major changes in line with the three phases were identified:(a) designing and implementing a number talk serving the learning goal; (b) designing and implementing a major task for achieving learning goals; and (c) orchestrating sharing of student work to highlight the learning goals. The description of lessons and the identification of the major changes were sent to the second author for review, who agreed with the analysis.
To triangulate this analysis from the participants’ perspective, the researchers also analyzed the teachers’ responses to the question, “Comparing the two research lessons, what were the main changes which were made, and what were the reasons for making these changes?” in their interviews (D5). Both teacher participants explicitly indicated these three major changes. For example, Ms. Brown explicated the first two major changes by saying,
We changed the number talk at the beginning of the lesson because with the first lesson, there was some discussion about the differences between layers and dimension, these vocabularies were confusing to the students.… In the rugs that we were making needed change to be rectangular because in the first [lesson] it just said a rug, so we kind of specified that a little bit….
For another example, Ms. Green highlighted the third change by saying,
We wanted the students to sequence what they shared. Um, in the first one, we kind of just called students up to share.… We are systematic in the ways that we had students to share their work in the second lesson. And I thought that was very impactful.…
After determining the three critical alignments (CAs; e.g., salient improvements), debriefing sessions (D3) were analyzed to reveal the causes of these changes. Keeping the three CAs in mind, we analyzed debriefings by asking the questions: How did the group identify the weakness? What were proposed solutions to the issue? What were the rationales for the proposed solutions? (Bannister, 2015). Relevant episodes were located to answer these questions to paint the pathway toward the three CAs.
Third, to answer the second research question, the interview data (D5 and D6) were analyzed using constant comparison (Corbin & Strauss, 2008) to identify participants’ perceived usefulness of TALS and benefits of participating in TALS. Three interview questions (4-6) addressed this research question. The first author read teachers’ and specialist’s interview transcripts carefully line by line and took notes to identify major themes of their responses. Then, based on analyzing Ms. Brown’s responses and corresponding notes again, a tentative category of major themes was created. Then the tentative categories were applied to code Ms. Green’s interview data and necessary modifications were made to generate a coding system.
Furthermore, the specialist’s interview (D6) was used to further triangulate and finalize the coding system. Based on the finalized categories, the first author identified relevant quotations to illustrate. The table, once created (including categories and illustrative quotations), was sent to the second author for review, and no significant changes were suggested.
Results
The results are presented in alignment with research questions. First, the major changes across the two research lessons are illustrated from a perspective of critical alignment. Second, the teachers’ perceived benefits from participating in the TALS are described.
How TALS Promotes Teacher Learning
Before illustrating each critical alignment, we briefly describe the research lessons as background.
Overview of the Two Research Lessons
Both lessons followed a similar structure, consisting of three phases. They began with a number talk, which focused on reviewing relevant concepts such as area, perimeter, and multiplication, leading to the major topic of the lesson (area model of multiplication). Then, a challenging contextual problem was assigned for students to work on individually, followed by discussion in groups of three to five students, with the teacher monitoring students’ work. Then several students were invited to share their solutions with the whole class. Figure 4 briefly summarizes the iterations of key components of the lessons, foreshadowing the critical alignments discussed below in detail.
Figure 4 Iterations of Key Components of the Lessons

Research Lesson 1. The lesson took place in Ms. Brown’s class with 20 students (15 had permission to appear in the video). Ms. Brown first led a number talk called “Which One Does Not Belong?” Students shared their observations, such as “The bottom does not belong because it is a longest rectangle with only two colors.” After appreciating students’ multiple strategies from different perspectives, Ms. Brown launched a contextual task:
Crystal wants a rug for her living room. She asks a rug maker to make a rug with an area of 36 square feet. The rug maker realizes there is more than one way he can make the rug, so he decides to make rugs of all the possible dimensions and then let her choose. What are all the dimensions of all the rugs that he could make? Use pictures, equations, or words to model your thinking. (Extension: Can you design a rug that is 36 square units but not a rectangle? Record your thinking and prove it is 36 square units. Use a diagram and equation.)
Students were provided the following materials: a task recording sheet, grid paper, colored pencils/crayons, and 36 square tiles. After clarifying what the task was asking, students first worked individually. Then, Ms. Brown organized students into groups (four or five students) to discuss their solutions. Three students were then invited to present and explain their solutions to the entire class. Finally, the class ended with the teacher’s summary that there are many possible solutions and the importance of using multiplication to find area.
Research Lesson 2. During the first debrief, the RL1 was highly acclaimed in terms of student engagement, teacher questioning, student productive struggles and rich discourse, and multiple students’ solutions and sharing. However, some revisions and suggestions were discussed in response to concerns about the disconnect between the number talk and the major task and the wording of the major task. Thus, options provided to the students in the number talk and the wording of the major task were revised.
Following a similar structure, RL2 was taught in Ms. Green’s class of 18 students, with 12 of the 18 having permission to appear in the video. Both teachers and knowledgeable others were satisfied with the improvement of the second lesson. The lesson plan is available in Appendix C.
The Critical Alignments
The following three critical alignments evidence growth of the TALS team. Data from research lessons (RL) and debriefing sessions (DB) will be used to illustrate these alignments through the TALS process.
Critical Alignment 1 – Designing and Implementing Number Talk Serving the Learning Goals.
Engagement. The number talk was revised over the enactments of the RLs to focus on review of key concepts closely related to the major content goal: area model of multiplication. Shapes used in the number talk in both RLs were revised as shown in Figure 5. In the RL1, the number talk was used successfully to engage students in observing the shapes from different perspectives visually (such as two layers vs. one layer; patterns and squareness; two colors vs. multiple colors).
Figure 5 Three Versions of the Shapes Presented to the Students in the Number Talk

Imagination. In the first debrief (DB1), the researchers and teachers noticed that the number talk did not draw student attention to the area model of multiplication, but instead to volume because of the inclusion of a shape with two layers, which was a distraction. Thus, it was agreed that linking cubes should be replaced with square tiles. Furthermore, Dr. Johns suggested the desirability of the concepts of area and perimeter arising in the number talk. For example,
We may design a shape where there is one with the perimeter over 30 while the others with the same perimeter, so that students can identify the one does not belong based on their perimeter. But the focus should be on area. (DB1).
Finally, the group decided to remove the shape with two layers, which elicited a discussion of volume and redesign the shape using square tiles to elicit the contrasting ideas of area and perimeter.
Alignment. Ms. Haden redesigned the number talk as shown in the middle of Figure 5. In RL2, in the number talk there was rich and long discussion about area and perimeter. For example, students suggested the top shape did not belong because it is not closed or is without the middle part.
With the guidance of Ms. Green, students also calculated the area of each shape. Students mistakenly said the area of the top shape is 30 (it is 22 square units), but the teacher did not notice. Many errors occurred regarding perimeter, such as stating that the perimeter of the top shape is 26 units (missing the inner segments) and the perimeter of the shape on the right is 30 (it is 34). During the debriefing session, researchers pointed out that the top shapes (rectangle without the middle part) confused students regarding area and perimeter and did not help students understand the area model of multiplication.
Dr. Rose further illustrated students’ misconceptions about the area and perimeter of the top shape and said,
The task just distracted the learning goals of the lesson. We are focusing on area, not perimeter. Therefore, my suggestion will be another version [shown in right column of Figure 5]. All shapes are rectangles. Three of them are of area of 24, while the other one is greater than others.
Dr. Long also agreed: “We should have actually had the outline of the rectangle.”
Summary. Through the cycles of engagement-imagination-critical alignment during the LS process, the number talk was changed from superficial engagement (from focusing on colors and three dimensions) to focusing on area and perimeter with the intended emphasis on the area model for multiplication.
Critical Alignment 2 – Designing and Implementing Major Task for Achieving Learning Goals
Engagement. The major task, Crystal’s Rug, is a complex contextual task, designed to elicit students to apply the area model of multiplication and find multiple solutions using tools and the commutative property. In both RLs the task was implemented through private think time, then group discussion, and finally whole classroom sharing. In the RL1, the task was implemented successfully regarding productive struggle and eliciting rich discourse and multiple solutions to the task, but some students were confused with the extension problem (make irregular shapes). The only successful attempt involved using counting all strategies, not the goal of learning.
Imagination. During the DB1, the issues related to the task design were mentioned, specifically the extension task not extending students’ learning and minor language errors in the task. Ms. Brown shared her struggle with helping students advance when solving the extension problem:
There was one group that with the extension seemed to have a hard time.… All four of them were trying to make shapes that would not have been possible with the tiles, like a circle, and I wasn’t really sure, and we were running out of time.… I don’t know that I would know exactly how to guide them away from that without saying. “No, you can’t make a circle.”
The confusion caused by the ambiguous language of the task led to some discussion about modifying the task. For example, Dr. Long suggested putting “rectangular rugs” in the beginning of the task. Finally, the group decided to delete the extension problems (because the only strategies the students had for calculating the area of an irregular polygon involved counting, which was not the focus of this RL). The group also decided to modify the major task as had been discussed.
Alignment. In the RL2, the revised task was used. Due to removing the extension problem and limiting the possible rugs to rectangular rugs in the major task, the model of multiplication was the primary focus. Thus, sharing students’ work in the whole class was focused on the model of multiplication (real context vs. mathematics models) and relevant properties (such as the commutative property). Overall, due to the inclusion of the language “rectangular rugs,” the RL become more coherent and focused on the goals of learning.
During the second debrief, Dr. Johns identified an issue:
I think about the term of dimensions. I think there’s still an issue with language in the task. In terms of decontextualizing and contextualizing that, I think we might need to think about how to clarify the questions. But I don’t know. Sometimes, we pick a task, but we need to strengthen that task. We as a group should really think about mathematical correctness. I think there are some issues with the task question.
Then, the group carefully discussed formulating the questions of the task. A new version was created by Ms. Haden based on this conversation: (a) List all possible dimensions of rectangles which are used to model possible rugs that the rug maker could make for Crystal; and (b) list all possible rectangular rugs that the rug maker could make for Crystal.
Summary. Through the process of engagement-imagination-alignment, the task was revised and refined to include more precise language and to focus on the major goals of learning (both content and mathematical practices).
Critical Alignment 3 – Orchestrating Student Work to Highlight the Learning Goals
Engagement. In the RL1, three students were invited to share their solutions. Student 1 explained her six solutions as follows:
So, I used equations to solve this problem. I did multiplication and division. I didn’t get to finish my division…. So, I did 12 times 3 equals 36. I did 18 times 2 equals 36. 6 times 6 equals 36. 1 times 36 equals 36. 9 times 4 equals 36, and 3 times 12 equals 36. So, all the ones I said at the top, I switched at the bottom so that they would, because they would turn the carpet around. It would make it different. It would make a different shape in her room, in her living room, so it would, so if she wanted, so if it was like 4 times 9, if she had it, if she couldn’t fit it as 9 times 4, she could turn it the other way so that it could fit in her room.
Student 1 explained five different designs using equations and explained why 4 times 9 and 9 times 4 are different in terms of the contextual situation (fitting a room). Then Ms. Brown highlighted that the student used “the commutative property” to switch factors around and get more equations. The student said that she switched some of them on her graph paper.
Student 2 explained his seven solutions (12 × 3 = 36, 3 × 12 = 36, 18 × 2 = 36, 6 × 6 = 36, 36 ×1 = 36, 9 × 4 = 36, 9 × 4 = 36) and asked Ms. Brown if he could present the extension. After confirmation, Student 2 showed his “Crazy” design, and explained how he proved his answer using a counting all strategy.
The third student showed his six solutions. In particular, he explained how to compute 4 times 9 by drawing nine circles of four tallies in each, and then using 18 plus 18 to get 2 times 18. It is clear the student still performed multiplication as repeated addition.
Imagination. During the DB1, both knowledgeable others and teachers appreciated that the students engaged in productive struggle facilitated by Ms. Brown’s purposeful questioning (accessing and advancing questions, rich discourse, and productive and accountable sharing of students’ solutions). For example, Ms. Haden said, “You did not give them a statement; you did not give them the answer, but always asked questions. So, I felt like those were all strengths.”
In addition to strengths, the team also discussed possible improvements. One aspect was about sharing students work. Ms. Haden wanted to know the rationale behind selecting the three students to share in the order chosen. Dr. Rose was concerned about the wisdom of sharing each of these solutions and strategies in terms of the stated goals of the lesson.
Then, Ms. Brown responded that she chose the first student because the student used the language “commutative property” and was “thinking of the tasks in the real world, like this is a real rug.” The second student was selected because of her use of the repeated addition strategy and her excitement to share her solution to the extension problem.
However, Dr. Rose pointed out the major goals of the RL1 were making sense of the area model of multiplication, finding dimensions of rectangles when given the area, and the commutative property.
Just to talk about final sharing. I liked when you said we can build on each other’s idea. If we have our goal and then, finally, it’s a good place to put everything together along your goal. I think there are some big ideas. Number one is commutative property. So, one student should talk about that. And number two is about the area model. We can draw a rectangle to represent [multiplication]. So, one student should talk about area model.
Moreover, the group discussed the importance of listing all possible solutions systematically. However, Dr. Johns raised another critical point: What is our correct answer? Are there nine solutions or five solutions exactly? After discussion, the group agreed that there are five solutions to the original contextual problem, but students should list nine different sets of dimensions of rectangles to model rugs. Dr. Johns clarified a key point about “contextualized solution” vs. “decontextualized solution” and answers to the real-world task. A 4 by 9 rug is the same rug as a 9 by 4 rug, the orientation is just different. So, there are only five different rugs, while there are nine multiplication facts having a product of 36.
Thus, the group agreed that in the final sharing of students’ solutions should focus on: (a) area model of multiplication (commutative property), (b) listing all nine possible solutions systematically (decontextualized solutions) and explaining the final five solutions (contextualized solutions).
Alignment. In the RL2, Ms. Green asked three students to share their work as shown in Figure 6.
Figure 6 Samples of Student Work in RL2
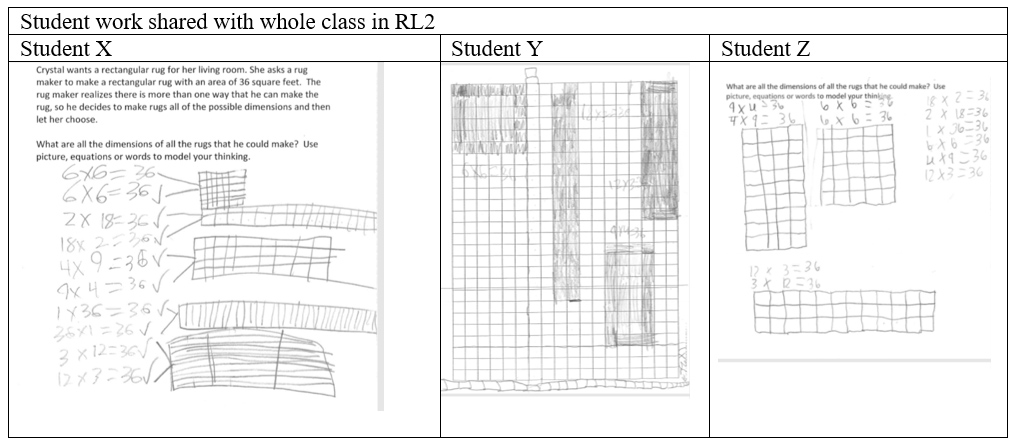
Student X explained her nine solutions systematically using the commutative property (drawing diagrams and writing equations), as evidenced by the following interactions:
Student X: So, what I did is, I did 6 times 6 is 36, and you can flip it around, but it would be using the same numbers. And then, I did 2 times 18 equals 36, and 18 times 2 equals 36. And I did 4 times 9 equals 36 and 9 times 4 equals 36 and 1 times 36 and 36 times 1. Then, I did 3 times 12 equals 36 and 12 times 3 equals 36 and to check it is, I went back with the tiles and did all of them and put a checkmark that I did them.
Ms. Green: So, I see that you said you flipped it around, so what did you mean by you flipped it around?
Student X: I used commutative property.
Ms. Green: Okay, so just changed the shape, the orientation, the way the rectangle is turned. Okay, so that gave you, that gave us how many total ways to make the rug? How many did we come up with on that?
Student X: 9
Student Y from another group shared his five solutions:
Student Y: I did 6 times 6 equals 36, 6 across and 6 going down. I did 18 times 2, which is 18 going down and 2 across which is 36. I did 12 going down and 3 across which equaled 36. I did 9 going down and 4 across which also equaled 36.
Ms. Green: I saw when [Student Y] started, he immediately went to this paper and started putting his model on the paper and then he went and added the equation back with it. Did you put any, I see you have a total of how many on here?
Student Y: Four. Well, the fifth one’s at the bottom.
Ms. Green: The fifth one’s at the bottom, okay, yep. What was the fifth one?
Student Y: 1 times 36
Ms. Green: So you had five where [Student X] had nine on there, so we’re gonna come back and talk about the difference between those two, why [Student Y] got five and why [student X] got nine, and we’ll have a discussion at the end. And then, I want [Student Z] to share her thinking. And [Student Z], I want you to share us talking about how you started off finding rugs that would work with an area of 36, your strategy.
After the two students presented their solutions, the teacher drew students’ attention to the difference in the number of total solutions and emphasized it would be discussed later. A third student presented six solutions (9 × 4 = 4 × 9, 2 × 18, 1 × 36, 3 × 12, 6 × 6) and explained how he found 4 × 9=36 using tiles. The student used division and multiplication to find six solutions, but he said that “he did not draw all of them.”
Building on the conflicts created by different answers to the same task, Ms. Green asked the class to look at the original question and discuss what the correct answer should be. At the beginning, Student Z still believed that the answer should be nine solutions:
If you look at it [rectangle], the width is gonna be switched. The width would probably be 2 and the length would be 18, and then it switched again and 18 would be the width and the length would be 2. If we turn it around, it will be a different length.
Ms. Green further asked a specific question:
Okay, so if I said that this rug [Real-world contextual task] was 18 feet long and only 2 feet wide and I had it going this direction, then, I said, Oh, I want to turn it the other direction, does that make a different rug? Is it the same rug or a different rug? What do we think? Same rug? Tell me why.
Then, Student Z realized, “You’re using the same numbers (18 and 2), so it would be the same answer, the answer would still be 36 because you’re just flipping where you put it.” Then Student X changed her answer to 5. And student Y further explained that “the real amount is five, but I get how she got nine, because if you just switched all of them around except for 6 times 6, then you got nine, but if you didn’t, the real amount would be five.”
Finally, Ms. Green highlighted by saying,
Do we agree, we think there’s five? Five [different solutions] total.… Great job listing them all. We really found all the different ways and all the different dimensions [for modeling the de-contextualized problem], but then, you have to go back to our [original context] problem and decide what our problem is asking us to find.
During the second debrief, all teachers and researchers appreciated the improvement in the selection and sequencing of student work to share with the whole class. Ms. Green said,
Once they got into the task, they really dug into constructing the area model and then translating that onto the graph paper. Like, that’s where I almost saw every group go to was, they built their model, they were using their tiles, and then they were transferring that with the equation already to the grid paper, which I thought was great.
Ms. Brown said,
I thought they did a really good job connecting the concrete to the abstract. I noticed a lot fewer of your kids listed nine ways. Like, a lot of them didn’t even need to kind of be prompted to say, “Are there really nine ways or are they only five ways?” They did a really good job in that.
Dr. Rose said,
I think [the teacher] did an excellent job in connecting the student work among different solutions and particularly that main idea about decontextualization and the contextualization. So, students really understand why the total is nine ways, but we need five ways.
Summary. Through these cycles of engagement-imagination-critical alignment, the participating teachers moved from sharing solutions based on teacher’s personal interest, to sharing students’ solutions based on the learning goal of the lesson.
The Usefulness and Effects of the TALS from the Insiders’ Perspective
The Usefulness of the TALS
The major strengths of TALS presented by teachers and the Ms. Haden in their interviews were as follows:
Watching Colleagues’ Teaching Without Missing Own Lessons. Both teachers were excited about the opportunity to watch colleagues’ lessons without missing their own classes. Ms. Brown recognized the major benefit was that
I could observe another teacher, learn from her, without losing any of my own class time. It was fine to be able to see inside someone else’s classroom and watch someone else teach and watch someone else’s students to see how they’re working in comparison to mine without having to take time away from my own kids.
Similarly, Ms. Green said, “I was able to watch her lesson, the first lesson, um, on my own time. I didn’t have to leave my students, um, and my teaching and things that I need to cover to go watch her.” Ms. Haden appreciated that “we didn’t need to pull teachers out of classrooms, that everything that we did was during their planning times … but we had the option of after school if they wanted that.”
Better Ability to Examine Student Thinking. Both teachers and Ms. Haden appreciated the enhanced opportunity to examine individual students’ thinking in detail by watching small group videos. For example, Ms. Green explained,
The small group videos were very helpful. A lot of the times I’m walking around when students are in group work and they’re having great conversations while I’m there. But then often when I walk away, they go back to working on their own or they go back to not really sharing with others and… So I thought that the small group videos were helpful in seeing what students do when I actually walk away. Like, are they continuing to work? Is their conversation still rich? Are they still, um, persevering through the task? And so, I thought that those videos were helpful to see what students are still doing even when I’m not there.
Ms. Haden also recognized that
with the Swivl camera, the power of seeing what the students were discussing and what they were doing when the teacher wasn’t there and we could catch, capture every small group, what was happening there, I felt like that was a huge strength.
Examining the Research Lesson in Depth Through Using the Annotated Videos. Both teachers and Ms. Haden realized the power of using the annotated videos for watching and reflecting. For example, Ms. Brown expressed how the annotated videos benefited her:
When I was viewing the other video and I noticed that you could click on the comment and it would, um, move the video to the exact spot that the comment connected to. And so that was helpful to me just when I was, was reviewing. It’s helpful to watch it through one time, but it’s always good to have another perspective. Some people might think of things that you don’t think of yourself when you’re watching it, and so I could see a comment and think, “Oh, I didn’t notice that the first time. Let me click this.” It takes me back to that moment in the video and I can rewatch. So I, yeah, I loved that comment section.
From a specialist’s perspective, Ms. Haden spoke to the advantages of the teachers being able to see questions and comments to be addressed in the debrief as they first saw the lesson via the annotated video.
So, I felt like this was better in the sense the teachers knew some of the comments and some of that, whatever I had written up there when they watched the video. And so, they were able to address that. Like, you know, therefore we did this, and this is why we pose this question. And so, I felt like it did help the discussion that everybody had kind of known some of that.
In the annotated video (RL2), Ms. Haden posed 20 comments and questions that were intended to draw teachers’ attention to critical learning moments in class, to link them to mathematical practice, and to pose questions for further thinking to be discussed in the debriefs. Both debriefing sessions and interviews with teachers and the specialist demonstrate that the annotated videos helped the teachers reflect upon their teaching in depth and promoted productive discussion in postlesson debriefs.
Conducting Debriefing Session Through Zoom. The teachers and the specialist appreciated the convenience of using the video-conferencing system. Ms. Brown realized that “we weren’t able to connect in person every time, but we still video-conferenced, and that went really well.” The specialist Ms. Haden noticed,
in our debrief with Zoom we could actually draw a conversation out from some of those comments. So, I thought that was really strong. … I was very comfortable with Zoom, and it was nice from my point of view because I was actually in a meeting till five minutes before, and I just was able to walk in. I didn’t have to worry about driving to a school, and everybody came online. I mean, it really went extremely smooth. The teachers were able to come at a time that was convenient for them because I think they set the time, and because of Zoom, I’m like, that will work. And um, and then, yeah, so other people at different locations, I felt like it really went surprisingly smooth.
The Effect of TALS on Teachers’ Perceived Learning
In agreement with the critical alignments previously described, the teachers perceived their gain from participating in the TALS to include (a) Clarifying and achieving learning goals of the lesson; (b) learning to design mathematics tasks; and (c) developing teacher knowledge needed for teaching.
Clarifying and Achieving Learning Goals of the Lesson. Ms. Brown explained her learning in specifying and targeting learning goals through the TALS process:
So, I thought that a major benefit was we kind of came into this [TA]LS not really knowing where we wanted to head with it. So then once we started talking about it, we really came up with our learning goal, um, of relating area to multiplication and division. And so, um, I thought that taking that learning goal, we knew what we wanted students to achieve in this and then working out from there, I thought that that was powerful. Um, we thought we came up with, um, a great lesson, um, really looking at the math standards and the math practice.
Learning to Design Mathematics Tasks. Both teachers recognized their development in designing tasks (number talk and major challenging tasks). Ms. Brown explained,
I think all debriefing that we did and the discussion when we were choosing what tasks we wanted to do was really beneficial because it was nice to have so many other perspectives on how this could go or how it went.
Ms. Green appreciated that
in the task we really were able to look at like the wording in the task and see that, um, see where we could even strengthen just the wording of the task itself to make sure that students were going to get where we wanted them to be by the end of the process.
Developing Teacher Knowledge Needed for Teaching. Both teachers emphasized learning from others’ input through the TALS process. Ms. Brown said,
Bringing in four extra people that I haven’t worked with before really shed a lot of light on things I did not think of. I mean, I came away from the first debrief with a lot to chew on. I kind of took it home and thought, “You know, it is these certain comments are making me look at this lesson and this task in a completely different way.” Um, and so I think that those conversations were, were invaluable.
Ms. Green expressed the helpfulness of the entire process of teaching-debriefing-revision and reteaching:
I thought that by going through this process, my own knowledge about setting learning goals, what I need to do and how I need to approach it, the questions that I need to ask, the tasks to pose, number talks to tie with it [were strengthened.] I thought that the whole process really just strengthened my teaching and overall content knowledge of this area of math. …. Everything just ties together and promotes teacher knowledge.
In addition to the perceived strengths of TALS and major benefits from participating in TALS, some possible constraints of implementing TALS were mentioned. These include distracting students’ attention due to the use of the novel technology and availability and stability of the technology. According to Ms. Brown,
The constraints with technology are always going to be, its availability…. Do we have the money for it? Uh, is there enough to where I can have it when I need it? Am I sharing with other teachers? That sort of thing. Um, and then just, I think that the technology worked really well in my room, and I think they had maybe one issue in the second lesson. So with technology, I guess a constraint is always that you don’t know if it’s going to work for you that day until you plug it in and try it, which is just not anything I think you can help.”
Ms. Green realized some distraction due to the newness of the technology in saying, “A couple of students were caught looking at it, and I even felt myself a couple times, like making sure it was tracking me.” She believed, however, that
the more and more that students had it in groups and they were familiar with it being there and set up and turned on, I think that that would wear off. So, I think that that really was the only constraint with the technology. But I think it would get better with time.
However, the specialist made positive comments: “The technology is not cumbersome. It does not require days and days of training. So, the technology itself is easy to implement.” In addition, she said that schools should be able to find resources:
I think, um, especially our title schools that have the funding, you know, they could actually purchase— and we know we’ve got a couple schools that are already looking at it because of hearing about Swivl and what, what the capabilities are.
Conclusion and Discussion
This study demonstrated that TALS may improve teaching and develop teachers’ knowledge for teaching as a traditional LS does (Huang & Shimizu, 2016; Lewis & Perry, 2017). This TALS promoted improvement of the research lesson in the following ways: sharpening and achieving learning goals; improving and implementing major instructional tasks; and productively orchestrating discussion around student work.
More than a traditional LS could offer, this TALS removed teachers’ and knowledgeable others’ issues of scheduling and traveling. The capability of the Swivl system to record multiple videos (of the teacher and individual student groups) simultaneously and the capability for the videos to be annotated provided teachers with flexibility and power of examining student thinking and reflecting on their teaching beyond what a traditional LS could provide. The ease of use and availability of these kinds of technologies could make the TALS implemented at scale.
Thus, overall, this study reveals that TALS has potential to yield the similar effects of traditional LS while removing the obstacles of scheduling issues (missing classes) and possibly strengthening teaching and learning of mathematics within TALS. In addition to these positive results, the following intellectual contributions and practical implications are discussed.
Enriching the Theories of CoI
This study enriches the theory of CoI in several ways. First, by incorporating critical alignments from the concept of CoI (Jaworski, 2006), the learning process of participation and reification within a CoI has been refined as observable phases of engagement, imagination, and critical alignment. In particular, the critical alignment could be made through identifying issues in the research lesson, proposing solutions, and enacting the hypothetical solutions.
Second, although researchers have tried to theorize teacher CoP through utilizing frame analysis (Bannister, 2015; Horn, 2007), it has been constrained at the level of intended learning within a CoP by identifying prognostic and motivational frames. Yet, this study focused on the interactions between intention and enactment via collective reflections, and vividly demonstrated how the intended plan could be realized in practice.
Third, this study contributes to deepening understanding of principles of cultivating CoP (Wenger et al., 2002). For example, this study illustrated the importance of knowledgeable others bringing their perspectives into the TALS CoI to leverage the learning of participating teachers, as well as the importance of developing healthy norms and a critical inquiry stance within the TALS CoI when evaluating and improving lessons.
Enriching Theoretical and Methodological Approaches to Studies on LS
LS has been adapted widely around the world, yet the theories of and methodologies for researching LS have recently become an emerging field to explore (Huang et al., 2019a; Quaresma et al., 2018). Due to the situated and collaborative nature of LS, several sociocultural situated theories have been employed in the study of LS, such as CHAT activity theory (Wake et al. 2016), and CoP (Corcoran, 2011; Sato et al., 2019).
Although CoP has been claimed as a theoretical framework in several studies of LS (e.g. Corcoran, 2011; Sato et al., 2019), it has been mainly used to interpret results, but not used as an analytical tool. This study is the first attempt to explore how CoI (Jaworski, 2006) could be used as a theoretical perspective and an analytical tool in examining teacher learning in TALS. Specifically, the three phases of engagement, imagination, and critical alignment help to understand the interactions of planning, enacting, and evaluating of research lessons so that teacher learning is evidenced in detail.
Structurally like design-based research (Cobb et al., 2017) because of the involvement of knowledgeable others and repeated teaching of the same content to different groups of students, the iterative process of TALS (plan-do-reflect-revise-redo) provides participating teachers with opportunities continuously and critically to engage-image-align to gear toward a higher level of critical alignment (as shown in Figure 3). Thus, this study contributes to developing an enriched CoI framework and analytical tools for study on LS, in general.
Enriching the Use of Various Technologies to Strengthen LS
Using various technologies to support teacher learning through examining classroom videos is not new (e.g., Beisiegel et al., 2017; Borko et al., 2011). In Skultety et al. (2017), participating teachers improved their lesson planning skills through face-to-face examination of self-videotaped research lessons (focus on whole class teaching) and researcher-generated animation (focus on virtual students’ learning). However, it was hard to obtain authentic student learning artifacts in this approach.
In Choppin et al.’s (2020) synchronous online model, the participating teachers examined expert teachers’ demonstration lessons in a virtual environment. Although the productive discourse surrounding a well-developed demo lesson was found to be beneficial to participating teachers’ learning, with this approach teachers do not have an opportunity to reflect on their classroom implementation. Thanks to the merits of the TALS model (cycle of plan-do-reflect-revise-redo) and integrative use of technologies (Swivl and Zoom), this study demonstrated a novel approach for teachers’ learning: bringing together authentic student learning artifacts (three student-group videos), the ability to extensively and collectively examine student learning (reviewing annotated videos), enaction of what teachers learned in their classroom (research lessons), and collaborative reflection on their implementation (debriefing discussion).
Possible Limitations and Practical Implications Regarding the Technology
Three possible constraints of using the technology were identified by the teachers in this TALS. One is the possible distraction to students because of the novelty of the technology. However, out of 2 hours of video collected with 27 students, only two instances of students seeming to be distracted by the cameras occurred. In the small group videos, two students were off task performing for the cameras. In light of the low occurrence of this phenomenon, the teacher believed that this possible constraint could be eliminated as the novelty of the technology wears off.
A second possible constraint is the reliability of the technology. Likewise, this possible constraint is also viewed as minimal. Only one instance of a reliability issue occurred during this exploratory study, and the issue was quickly resolved. At one point in the second lesson, the robot stopped tracking the teacher when she moved to the back of the room. It was turned back to face the teacher, and it began tracking again. The teachers and math specialist on the TALS team agree that the technology is easy to use.
A third possible constraint voiced was the availability of the technology. However, the district mathematics specialist did not feel this challenge was formidable because of the relatively low cost of the equipment and the potential availability of funds such as Title II funds in the US that could be used for this purpose.
Based on our experience in using the Swivl robot in this exploratory study, we offer some practical suggestions regarding the use of the technology with TALS (see Appendix D for details). These suggestions involve logistics regarding placement of the Swivl robot, videoing small group work, viewing of the small group videos, and student sharing in whole group using a document camera.
Limitations and Further Studies
In this study, each of the first three authors is experienced in traditional LS, with a trustful working relation with the specialist, and they were involved in the process of the TALS in different ways. The duality of participants and observers in the study may help them get a deep understanding the process of TALS and data analysis. On the other hand, it may prevent them from providing objective perspective, although the researchers were aware of this bias and adopted participant check strategy. In addition, the findings of this small exploratory study are not guaranteed to be generalizable.
Two practical obstacles to scaling up LS have been identified: lack of accommodating teaching schedules to allow for live class observation and lack of trained LS facilitators (e.g., Akiba & Wilkinson, 2016). By eliminating the second variable (given an experienced LS facilitator), this exploratory study only aimed to address the first obstacle. Although the merit of this TALS is evident, it should be noted that the researchers and facilitator have played important roles in supporting the teachers to reflect and design the research lesson.
On one hand, this finding highlights the importance of involvement of knowledgeable others in LS to ensure the quality of LS (Takahashi, 2014). On the other hand, it calls for the imperativeness of developing qualified facilitators of LS (and TALS). Developing facilitators of PD has been an important field to explore (Borko et al., 2014; Lesseig et al., 2017). One promising result from this study is the success in using the video conference system Zoom for debriefing sessions. This strategy would allow for facilitation by an individual not in the building and thus would broaden the pool of possible facilitators.
More research about what knowledge and skills are needed for facilitating and how to identify and develop facilitators is needed. In addition, although the literature includes a great deal of studies on dialogic nature of postlesson discussions in a traditional lesson study CoI (e.g., Vivikki et al., 2017), but little is known about the nature of teacher discussion in a virtual TALS CoI (Choppin et al., 2020), which needs to be explored appropriately.
References
Akiba, M., & Wilkinson, B. (2016). Adopting an international innovation for teacher professional development: State and district approach to lesson study in Florida. Journal of Teacher Education, 67(1), 74-93. https://doi.org/10.1177%2F0022487115593603
Bannister, N. (2015). Reframing practice: Teacher learning through interactions in a collaborative group. Journal of the Learning Sciences, 24(3), 347–372. https://doi.org/10.1080/10508406.2014.999196
Bannister, N. A. (2018). Theorizing collaborative mathematics teacher learning in communities of practice. Journal for Research in Mathematics Education, 49(2), 125-139. https://doi.org/10.5951/jresematheduc.49.2.0125
Beisiegel, M., Mitchell, R., & Hill, H. C. (2017). The design of video-based professional development: An exploratory experiment intended to identify effective features. Journal of Teacher Education, 69(1), 69-89. https://doi.org/10.1177/0022487117705096
Borko, H., & Potrai, D. (2020, February). Teachers of mathematics working and learning in collaborative groups. The proceedings of ICMI Study 25. Lisbon, Portugal. http://icmistudy25.ie.ulisboa.pt
Borko, H., Jacobs, J., Koellner, K., & Swackhamer, L. (2015). Mathematics professional development: Improving teaching using the problem-solving cycle and leadership preparation models. Teachers College Press
Borko, H., Koellner, & K, Jacobs, J. (2014). Examining novice teacher leaders’ facilitation of mathematics professional development. The Journal of Mathematical Behavior, 33, 149–167. https://doi.org/10.1016/j.jmathb.2013.11.003
Borko, H., Koellner, K., Jacobs, J., & Seago, N. (2011). Using video representations of teaching in practice-based professional development. ZDM Mathematics Education, 43(1), 175–187. https://link.springer.com/content/pdf/10.1007/s11858-010-0302-5.pdf
Choppin, J., Amador, J. M., Callard, C., Carson, C., & Gillespie, R. (2020). Synchronous online model for mathematics teachers’ professional development. In P.Wachira & J. Keengwe (Eds.), Handbook of research on online pedagogical models for mathematics teacher education (pp. 176-202). IGI Global.
Cobb, P., Jackson, K., & Sharpe, D. C. (2017). Conducting design studies to investigate and support mathematics students’ and teachers’ learning. In J. Cai (Ed.), Compendium for research in mathematics education (pp. 208–233). National Council of Teachers of Mathematics.
Cobb, P., Zhao, Q., & Dean, C., (2009). Conducting design experiments to support teachers’ learning: A reflection from the field. Journal of the Learning Sciences, 18(2), 165–199. https://doi.org/10.1080/10508400902797933
Community for Advancing Discovery Research in Education. (2017). Emerging design principles for online and blended teacher professional development in K-12 STEM education. Education Development Center.
Corbin, J., & Strauss, A. (2008). Basics of qualitative research (3rd ed.). Sage.
Corcoran, D. (2011). Learning from lesson study: Power distribution in a community of practice. In L. Hart, A. Alston & A. Murata (Eds.), Lesson study research and practice in mathematics education (pp. 251-267). Springer.
Cravens, X., & Drake, T. (2017). From Shanghai to Tennessee: Developing instructional leadership through Teacher Peer Excellence Groups. International Journal for Lesson and Learning Studies, 6(4), 348-364. https://www.emerald.com/insight/content/doi/10.1108/IJLLS-12-2016-0062/full/html
Darling-Hammond, L., Hyler, M. E., & Gardner, M. (2017). Effective teacher professional development. Learning Policy Institute.
Desimone, L. (2009). Improving impact studies of teachers’ professional development: Toward better conceptualizations and measures. Educational Researcher, 38(3), 181-199. https://doi.org/10.3102%2F0013189X08331140
Dudley, P. (2014). Lesson study: Professional learning for our time. Routledge
Engeström, Y. (2001). Expansive learning at work: Toward an activity theoretical reconceptulization. Journal of Education and Work, 14(1), 133–156. https://www.tandfonline.com/doi/abs/10.1080/13639080020028747
Gersten, R., Taylor, M. J., Keys, T. D., Rolfhus, E., & Newman-Gonchar, R. (2014). Summary of research on the effectiveness of mathematics professional development approaches. Instructional Research Group. https://nces.ed.gov/pubsearch/pubsinfo.asp?pubid=REL2014010
Horn, I. S. (2007). Fast kids, slow kids, lazy kids: Framing the mismatch problem in math teachers’ conversations. Journal of the Learning Sciences, 16, 37–79. https://doi.org/10.1080/10508400709336942
Huang, R., Fang, Y., & Chen, X. (2017). Chinese lesson study: An improvement science, a deliberate practice, and a research methodology. International Journal for Lesson and Learning Studies, 6(4), 270-282. https://www.emerald.com/insight/content/doi/10.1108/IJLLS-08-2017-0037/full/html
Huang, R., & Shimizu, Y. (2016). Improving teaching, developing teachers and teacher developers, and linking theory and practice through lesson study in mathematics: An international perspective. ZDM Mathematics Education, 48, 393–409. https://link.springer.com/article/10.1007/s11858-016-0795-7
Huang, R., Kimmins, D., & Winters, J. (2019a). A critical mechanism for improving teaching and promoting teacher learning during Chinese lesson study: An analysis of the dynamics between enactment and reflection. In R. Huang, A. Takahashi, & J. P. da Ponte (Eds.), Theory and practices of lesson study in mathematics: An international perspective (pp.705-730). Springer.
Huang, R., Takahashi, A., & da Ponte, J. P. (2019b). Theory and practices of lesson study in mathematics: An international perspective. Springer.
Huang, R., Takahashi, A., Clivaz, S., Kazima, M., & Inprasitha, M. (May 2018). Lesson study in mathematics: Current status and its further directions. In M. Vianna (Ed.), The International Congress of Mathematicians 2018 Proceedings, Rio de Janeiro.
Jacobs, J., Seago, N., & Koellner, K. (2017). Preparing facilitators to use and adapt mathematics professional development materials productively. International Journal of STEM Education, 4 (30). https://doi.org/10.1186/s40594-017-0089-9
Jaworski, B. (2006). Theory and practice in mathematics teaching development: Critical inquiry as a mode of learning in teaching. Journal of Mathematics Teacher Education, 9, 187–211. https://link.springer.com/content/pdf/10.1007/s10857-005-1223-z.pdf
Jaworski, B., & Huang, R. (2014). Teachers and didacticians: Key stakeholders in the process of developing mathematics teaching. ZDM Mathematics Education, 46, 173-188. https://link.springer.com/article/10.1007/s11858-014-0574-2
Lave, J., & Wenger, E. (1991). Situated learning: Legitimate peripheral participation. Cambridge University Press.
Lesseig, K., Elliott, R., Kazemi, E., Kelley-Petersen, M., Campbell, M., Mumme, J., & Carroll, C. (2017). Leader noticing of facilitation in video cases of mathematics professional development. Journal of Mathematics Teacher Education, 20, 591–619. https://link.springer.com/article/10.1007/s10857-016-9346-y
Lewis, C. (2016). How does lesson study improve mathematics instruction? ZDM Mathematics Education, 48(4), 571-580. https://link.springer.com/article/10.1007/s11858-016-0792
Lewis, C., & Perry, R. (2017). Lesson study to scale up research-based knowledge: A randomized, controlled trial fractions learning. Journal for Research in Mathematics Education, 48(3), 261-299. https://www.jstor.org/stable/10.5951/jresematheduc.48.3.0261
Lewis, C., Perry, R. R., & Hurd, J. (2009). Improving mathematics instruction through lesson study: A theoretical model and North American case. Journal of Mathematics Teacher Education, 12(4), 263-283. https://link.springer.com/content/pdf/10.1007/s10857-009-9102-7.pdf
Murata, A. (2011). Introduction: Conceptual overview of lesson study. In L. C. Hart, A. Alston & A. Murata (Eds.), Lesson study research and practice in mathematics education: Learning together (pp. 1-12). Springer.
National Governors Association and the Council of Chief State School Officers. (2010). Common core state standards for mathematics. In Common Core State Standards Initiative. https://www.corestandards.org/Math/Practice
National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematical success for all. Author.
Pang, M. F., & Marton, F. (2003). Beyond ‘lesson study’ – Comparing two ways of facilitating the grasp of economic concepts. Instructional Science, 31(3), 175-194. https://link.springer.com/article/10.1023/A:1023280619632
Parrish, S. (2014). Number talks: Whole number computation, grades K-5. Math Solutions.
Quaresma, M., Winsløw, C., Clivaz, S., Ponte, J. P., Ni Shuilleabhain, A., & Takahashi, A. (Eds.). (2018). Mathematics lesson study around the world: Theoretical and methodological issues. Springer.
Robutti, O., Cusi, A., Clark-Wilson, A., Jaworski, B., Chapman, O.,Esteley, C., Goos, M.,, Isoda, M., & Joubert, M. (2016). ICME international survey on
teachers working and learning through collaboration. ZDM Mathematics Education, 48, 651–690. https://doi10.1007/s11858-016-0797-5
Soto, M., Gupta, D., Dick, L., & Appelgate, M. (2019). Bridging distances: Professional development for higher education faculty through technology-facilitated lesson study. Journal of University Teaching and Learning
Practice, 16(3). https://eric.ed.gov/?id=EJ1224005
Seleznyov, S. (2018). Lesson study: An exploration of its translations beyond Japan. International Journal for Lesson and Learning Studies, 7(3), 217-229. https://www.emerald.com/insight/content/doi/10.1108/IJLLS-04-2018-0020/full/html
Sherin, M. G., & Han, S. Y. (2004). Teacher learning in the context of a video club. Teaching and Teacher Education, 20, 163–183. https://doi.org/10.1016/j.tate.2003.08.001
Skultety, L., Gonzalez, G., & Vargas, G. (2017). Using technology to support teachers’ lesson modifications during lesson study. Journal of Technology and Teacher Education, 25, 185-213. https://www.learntechlib.org/primary/p/172139/
Smith, M. S., & Stein, M. K. (2018). Five practices for orchestrating productive mathematical discussions (2nd ed.). National Council of Teachers of Mathematics.
Snow, D. A., & Benford, R. D. (1988). Ideology, frame resonance, and participant mobilization. In B. Klandermans, H. Kriesi, & S. G. Tarrow (Eds.), International social movement research (Vol. 1, pp. 197–217). Jai Press Inc.
Takahashi, A. (2014). The role of the knowledgeable other in lesson study: Examining the final comments of experienced lesson study practitioners. Mathematics Teacher Education and Development, 16(1), 4-21 (EJ1046714). ERIC. http://files.eric.ed.gov/fulltext/EJ1046714.pdf
Takahashi, A., & McDougal, T. (2016). Collaborative lesson research: maximizing the impact of lesson study. ZDM Mathematics Education, 48, 513-526. https://link.springer.com/article/10.1007/s11858-015-0752-x
van Es, E. A., Tunney, J., Goldsmith, L. T., & Seago, N. (2014). A framework for the facilitation of teachers’ analysis of video. Journal of Teacher Education, 65(4), 340-356. https://doi.org/10.1177/0022487114534266
Vrikki, M., Warwicj, P., Vermunt, J., Mercer, N., & Van Halem, N. (2017). Teacher learning in the context of Lesson Study: A video-based analysis of teacher discussions. Teaching and Teacher Education, 61, 211-224. https://doi.org/10.1016/j.tate.2016.10.014
Wake, G., Swan, M., & Foster, C. (2016). Professional learning through the collaborative design of problem-solving lessons. Journal of Mathematics Teacher Education, 19(2–3), 243–260. https://link.springer.com/content/pdf/10.1007/s10857-015-9332-9.pdf
Wells, G. (1999). Dialogic inquiry: Towards a socio-cultural practice and theory of education. Cambridge University Press.
Wenger, E. (1998). Communities of practice: Learning, meaning, and identity. Cambridge University Press.
Willems, I., &Van den Bossche, P. (2019). Lesson study effectiveness for teachers’ professional learning: A best evidence synthesis. International Journal for Lesson and Learning Studies, 8 (4), 257-271. https://doi.org/10.1108/IJLLS-04-2019-0031
Xu, H., & Pedder, D. (2014). Lesson study: An international review of the research. In P. Dudley (Ed.), Lesson study: Professional learning for our time (pp. 29–58). Routledge.
Appendix A
Teacher Interview Protocol
First thank you so much for your strong support of the lesson study and allowing us to conduct the interview. In the interview, I will ask you several questions about your experiences gained from the process of participating in lesson study (such as lesson planning, viewing videos, and debriefings). You just share your true feeling and thoughts. All your experiences are valuable for the study. Nothing is good or bad.
- State your pseudonym and today’s date.
- What are your perceptions of the final research lesson? Does the lesson achieve the overall learning goals? What were the most exciting moments? What were major strengths? What were major weaknesses if any? Why? Provide details as much as possible.
- Comparing the two research lessons, what were the main changes you made? What were the reasons for making these changes? How do you think these changes benefited students’ learning? Provide details as much as possible.
- During the independent viewing of the videos, what do you think about the reflection questions? To what extent do they think they are helpful for analyzing the lessons?
- During the group debriefings, what were the most helpful parts? What were the less effective parts? Do you have any suggestions for the improvement of debriefing discussion?
- We used technology to capture the classroom teaching, view and discuss the research lesson. What do you think were the major benefits and constraints regarding the use of the technology to promote teachers’ learning? Do you see things we could change in how the technology was used to make it easier to conduct lesson study or to make the lesson study process better?
- Reflecting over the entire process of lesson study (collaborative lesson planning, teaching, viewing and debriefing and re-teaching), what are the major benefits you gained regarding mathematics content, students’ learning, teaching strategies, analyzing and reflecting on teaching practice?
- Reflecting over the entire process of lesson study, what are the major factors promoting or hindering your learning/development? Why? Provide details as much as possible.
- Based on your experience of this lesson study, to what extent do you think this lesson study can be scaled up? Do you have any insight into the development of productive PLCs by incorporating with LS?
- Are there other ideas that you would like to share?
Appendix B
Math Specialist Interview Protocol
First thank you so much for your leadership in carrying out the lesson study and allowing us to conduct the interview. In the interview, I will ask you several questions about your experiences gained from the process of leading lesson study (such as lesson planning, videotaping, viewing and annotating videos, and debriefings). You just share your true feeling and thoughts. All your experiences are valuable for the study. Nothing is good or bad.
1. State your pseudonym and today’s date.
2. What are your perceptions of the final research lesson? Did the lesson achieve the overall learning goals? What were the most exciting moments? What were major strengths? What were major weaknesses if any? Why? Provide details as much as possible.
3. Comparing the two research lessons, what were the main changes which were made? What were the reasons for making these changes? How do you think these changes benefited students’ learning? Provide details as much as possible.
4. To capture the classroom teaching using Swivl, what were the major strengths and/or constraints? Are there any challenges you think teachers will experience in using the equipment (after training)?
5. Compared with traditional debriefing sessions, what were the strengths and/or weakness of the online debriefing session (using online conference system such as Zoom)?
6. Reflecting over the entire process of technology-assisted lesson study (collaborative lesson planning, teaching, viewing and debriefing and re-teaching), what were the major benefits for you to lead lesson study to promote teachers’ learning, compared to traditional lesson study? Why? Provide details as much as possible.
7. Reflecting over the entire process of technology-assisted lesson study, what were the major factors promoting or hindering teachers’ learning/development? Why? Provide details as much as possible.
8. Based on your experience of this technology-assisted lesson study, to what extent, do you think this lesson study can be sustained at the school level with the support of coaches or lead teachers?
9. Based on your experience of this technology-assisted lesson study, to what extent, do you think this lesson study can be scaled up at the district level? What challenges may be faced when scaling up technology-assisted lesson study? What supports are needed to scale up the technology-assisted lesson study?
10. Are there other ideas that you would like to share?
Appendix C
Lesson Plan from Second Teaching With Notes for Final Revision
Appendix D
Practical Suggestions for Using Swivl Technology With TALS
- Before the lesson, one should think about where to place the robot to minimize the possibility that a small group will be directly between the teacher and the robot during the course of the lesson. We had to move the robot during the videotaping on the second teaching to avoid this; this could have been avoided by considering this prior to the start of the lesson. Also make sure any small groups which are not to be videotaped (if they exist) are sufficiently out of potential range of camera. Experimenting to note the camera angles is helpful.
- In the first lesson, the teacher video was stopped at the end of the first phase of the lesson and restarted in order to start the small group videos for the second phase of the lesson. In contrast for the second lesson, the video for the small groups was activated at the beginning of the lesson even though the students were not working in small groups during the first phase of the lesson. This eliminated the teacher video having to be stopped between phases one and two of the lesson in order to start the small group videos. Having the small group videos filming while not capturing anything important was not a distraction in subsequently viewing the videos as feared; it was not a problem for TALS team members to ignore the initial parts of these videos.
- For maximal viewing, it may be necessary for viewers of the integrated Swivl video to drag the particular video they wish to view into the larger window (the position of video M in Figure 2); after viewing this video they can drag another video to this window to view it. Rationale: In the debrief from the first lesson there was a comment about the choppiness of the videos for the student groups. Videos not in the larger video window seemed choppy even with high speed internet, but when a video was switched to the larger window it was no longer choppy. Viewing small group videos in the larger window also made it easier to see student work.
- It is recommended that the iPads for capturing small group work be carefully placed. During the first lesson, small groups had the choice of sitting on the floor, as they often did, or at tables. In the second lesson they worked at tables. This allowed the iPads for the small groups to be positioned much better in order to capture group interactions. Thus, on the second lesson small group interactions were better captured than on the first lesson. Still, students’ papers in the small group often could not be seen unless a student or teacher purposefully moved their work in front of the iPad, perpendicular to the table, where it could be captured. When the teacher came to monitor a particular group, she sometimes had students do this or she did so. In this case work on student papers could be seen when the small group video was played in the larger viewing window. Surprisingly this did not seem to be a distraction.
- The following is a suggestion if students are sharing their work using a document camera in a whole class setting. For the whole class sharing of student work in the final phase of each of the lessons, selected students put their work on a document camera. In both lessons, the teacher marker was placed on the student sharing the work so that the robot would track the student. However, in the first lesson the students stood by the document camera and pointed to various aspects of their work on their papers on the document camera as they talked; consequently the video picked up the students pointing to their work on the document camera, but it did not show the screen on which the work was projected. In the second lesson, students placed their work on the document camera and then walked to the screen and pointed to various parts of their work on the screen as they talked. This worked well in that now both the student and their work appeared on the video. It was determined that visibility of the work could have been improved with experimentation with the lighting and the document camera.
![]()