Technological tools have changed the landscape of mathematics teaching. In geometry, teachers can launch investigations by having students efficiently manipulate, measure, and analyze dynamic diagrams (Jackiw, 2001). The study of algebra can be facilitated by the graphing calculator’s ability to produce multiple representations of functions to be compared and contrasted with one another (Fey, 1989). The process of statistical investigation can be supported by software with the ability to import data quickly from the Internet for analysis (Finzer, 2002). Various other technologies, like online discussion boards (Groth, 2008), spreadsheets (Alagic & Palenz, 2006), and even robots (Reece et al., 2005), have been discussed in terms of their potential to support students’ mathematical learning.
The rapid expansion of available technological tools has prompted scholarly discourse about how Shulman’s (1987) construct of pedagogical content knowledge might be built upon to help describe the sort of knowledge teachers need for teaching with technology. Recently, the phrase “technological pedagogical content knowledge” (or technology, pedagogy, and content knowledge; TPACK) has been used to describe “an understanding that emerges from an interaction of content, pedagogy, and technology knowledge” (Koehler & Mishra, 2008, p. 17). Such a conceptualization emphasizes that TPACK is more than just the sum of its parts. It implies that teachers must engage with content, pedagogy, and technology in tandem to develop knowledge of how technology can help students learn specific mathematics concepts.
The emergence of the TPACK construct presents a dilemma: How can teachers’ acquisition of TPACK be assessed? Answering this question is necessary for determining the extent to which different teacher education programs and experiences foster the development of TPACK. Without viable assessment mechanisms, comparing approaches and making decisions about actions to take in teacher education is difficult.
Pragmatic issues like program accreditation and grant evaluation also highlight the need for TPACK assessment. Accreditation agencies (e.g., National Council of Teachers of Mathematics & National Council for Accreditation of Teacher Education, 2005) have begun to ask for data about prospective teachers’ abilities to utilize technology in mathematics instruction, and agencies that provide funds to purchase classroom technology often want assessment data on how teachers are using the technology purchased. Hence, the development of TPACK assessment mechanisms is vital for helping build the infrastructure for current and future teacher education efforts.
Two Contrasting Paradigms for the Assessment of Teachers’ Knowledge
One current paradigm for assessing mathematics teachers’ knowledge is primarily quantitative and psychometric in nature. The Learning Mathematics for Teaching (LMT) Project at the University of Michigan exemplifies such an approach (Hill, Schilling, & Ball, 2004). University faculty work to produce forced-response test items meant to measure mathematical knowledge necessary for teaching. The items are field-tested and sorted based on their psychometric properties. Ultimately, scales of items are constructed and disseminated to individuals seeking to measure the effect of teacher education programs on mathematics teachers’ knowledge acquisition. One of the chief advantages to the psychometric approach is that it produces sets of items that can be administered relatively quickly to teachers. The process of refining items and scales in response to empirical data has also contributed to theory construction and refinement about the types of knowledge needed to teach mathematics (Hill, Ball, & Schilling, 2008).
Another current paradigm for assessing mathematics teachers’ knowledge is primarily qualitative in nature and draws upon case descriptions of teachers’ classroom practices. Simon and Tzur’s (1999) idea of generating “accounts of practice” is rooted in such a paradigm. In generating accounts of practice, researchers study teachers’ classroom practices through the lenses of conceptual frameworks that identify important theoretical constructs for attention. The conceptual frameworks may be revisited in response to observational data. Ultimately, accounts of teachers’ practices are built that “can portray the complex interrelationships among different aspects of teachers’ knowledge and their relationships to teaching” (p. 263). One of the primary advantages to such an approach is that it is flexible enough to allow the researcher to focus on aspects of teachers’ knowledge that may have not been identified a priori in the conceptual framework. It also allows for the exploration of contextual factors that contribute to the knowledge that teachers exhibit in their classrooms.
The Assessment Framework
The approach to assessing TPACK described in this paper is in the tradition of the qualitative “accounts of practice” paradigm. It grew out of a lesson study (Lewis, 2002) professional development project. A lesson study cycle involves having a group of teachers collaboratively construct a lesson on a shared learning goal for students, implement it, observe the implementation, and then debrief on the strengths and weaknesses of the lesson. The debriefing may lead to another lesson study cycle in which teachers continue to refine their approach to teaching the chosen concept. Stigler and Hiebert (1999) drew attention to lesson study as a model of professional development in their comparison of mathematics education in the U.S. and Japan. They noted that teachers in the U.S. tend to work in relative isolation from one another when compared to Japanese teachers.
Whereas Japanese teachers regularly meet to plan, observe, and debrief on lessons, U.S. teachers generally do not. Hiebert and Stigler (2000) hypothesized that such differences in professional development contributed to achievement differences between students in the U.S. and Japan and suggested that lesson study be implemented in the U.S.
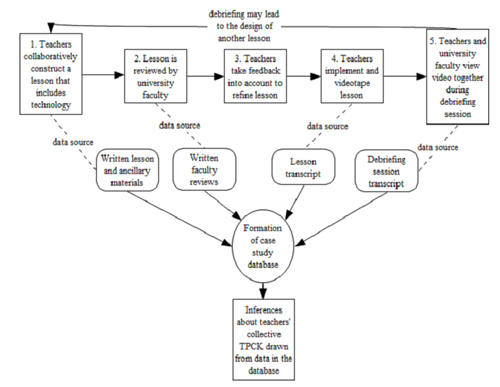
The lesson study process can generate a substantial amount of qualitative data for analysis, as illustrated in Figure 1. The rectangles in Figure 1 represent the phases in a lesson study cycle. Arrows between the rectangles indicate the progression that occurs from one phase to the next. The arrow from phase 5 (debriefing) to phase 1 (planning) shows that a debriefing session may spark a new cycle. The dashed lines extend to the qualitative data produced at each phase.
Arrows extending from the qualitative data sources indicate that the qualitative data can be assembled into a case study database (Yin, 2003), from which inferences about teachers’ collective TPACK are drawn. Further details about each phase in the process and how the process can be used to assess TPACK are provided in the remainder of this section. The assessment model built on this process will be referred to as the Lesson Study TPACK (LS-TPACK) model.
As indicated in Figure 1, the first step in the LS-TPACK model is that teachers collaboratively construct a lesson that incorporates technology in a school-based lesson study group (LSG). The type of technology and the learning goals for the lesson are not dictated to them by university personnel. Instead, teachers choose learning goals and accompanying technology for the lesson by identifying problematic concepts to address in collaboration with one another (Lewis & Tsuchida, 1998). Once learning goals and pertinent technology have been identified, the teachers use a four-column lesson plan format (Curcio, 2002) to write a lesson to be implemented by one of the members of the LSG. The four-column format the teachers are to use is shown in Figure 2. The primary goals of using the four-column format are to draw teachers’ attention toward matching instructional activities with students’ perceived learning needs and assessing students’ progress toward learning goals.
Figure 1. The LS-TPACK assessment framework. (Click on image for larger version.)
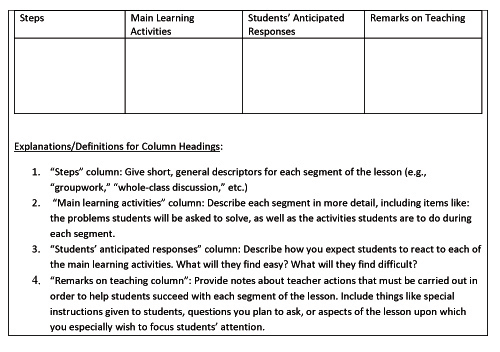
Figure 2. Four-column lesson plan format.
After the LSG writes the four-column lesson, it is sent to university faculty for review. Teachers also submit ancillary materials like worksheets and handouts to be used during the lesson. University faculty members are chosen to review the lesson based upon their teaching and research interests. The faculty reviews are solicited because previous research has illustrated that outside perspectives on the work of a LSG can help identify pedagogical and content-related weaknesses in lessons (Fernandez, 2005).
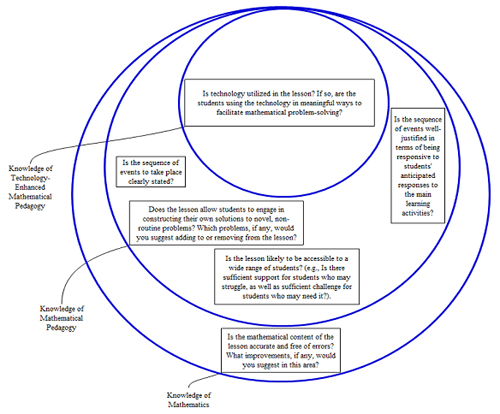
Reviewers are asked to comment on questions at three levels of specificity, as shown in Figure 3. The inclusion of the three levels of specificity resonates with Lee and Hollebrands’ (2008) observation that TPACK can be conceptualized as technological and pedagogical knowledge nested within content knowledge.
Figure 3. Questions reviewers are given to evaluate LSG lessons. (Click on image for an enlarged version.)
Within 2 weeks of the submission of the initial four-column lesson, university faculty feedback is sent to the LSG. The LSG is then left to decide which feedback will be used to refine the written lesson before it is implemented. At this point, university faculty members are involved in the planning of the lesson only if the LSG requests their help. This minimally invasive stance is taken to allow teachers to reflect on which pieces of feedback are feasible to build into the lesson and which ones are not.
Once the lesson has been refined based on reviewers’ feedback and teachers’ judgment, one member of the LSG teaches it. Another LSG member serves as videographer. The video is later viewed by all members of the LSG along with university faculty. Although it is often ideal to have all of the LSG teachers present in the room when the lesson is implemented (Lewis, 2002), video is used as a sharing mechanism to overcome obstacles associated with coordinating the schedules of all of the LSG members and university faculty members during the school day.
LSG members and university faculty view the lesson video together during a debriefing session at Step 5 in the lesson study cycle. To begin the debriefing session, the teacher who implemented the lesson and the videographer are asked to provide any contextual information that may help explain what will be observed in the video. After this information is shared, the video is played, and debriefing session participants are asked to take notes on perceived strengths and weaknesses of the lesson.
When the video is over, individuals participating in the meeting each share their perceptions of the strengths and weaknesses of the lesson. Initially, each person shares one perceived strength and one perceived weakness. The teacher who taught the lesson goes first during this portion of the session, and university faculty members go last. A more unstructured conversation occurs after each debriefing participant has shared perceived strengths and weaknesses. During the unstructured conversation, discourse may turn toward goals for the next, related lesson study cycle.
As shown in Figure 1, the LS-TPACK process produces qualitative data that are assembled into a case study database (Yin, 2003). The initial LSG four-column lessons and ancillary materials comprise part of the database. The lesson reviews written by university faculty comprise another part. Transcripts of the implemented, videotaped lessons and transcripts of debriefing sessions are also included.
To draw inferences about the collective TPACK of the LSG from the case study database, university faculty comments about teachers’ use of technology are compiled from the initial written reviews and the observations made during the debriefing session. These written and verbal observations are then compared against the LSG’s implemented lesson and teachers’ debriefing session comments. The comparison process is used by the project principal investigator to draw inferences about the nature of the teachers’ TPACK.
University faculty members who reviewed lessons and participated in debriefing sessions are asked to validate the inferences by revisiting, as necessary, the LSG’s initial lesson, the reviews they gave it, and the transcripts of the written lessons and debriefing sessions. The purpose of the validation step is to help ensure the production of trustworthy inferences (Cobb, 2000) about teachers’ TPACK.
An Application of the Assessment Framework
In one instance, the LS-TPACK framework was used to assess an LSG’s TPACK related to teaching systems of equations using graphing calculators. Two lesson study cycles related to this topic occurred within one academic year. The first cycle dealt with constructing a lesson for the general algebra I population at the school, and the second cycle’s lesson was for a group of algebra I students the LSG considered to be more advanced.
The first author drew inferences about the teachers’ TPACK by examining the case study database for these cycles, as described earlier. The inferences were then validated and refined when necessary in consultation with the second, third, and fourth authors of the paper, who served as university faculty reviewers and debriefers during the lesson study cycles. Three of the most salient TPACK inferences drawn and validated are offered in the next section. The three inferences helped form the foundation for future work with the LSG by identifying TPACK elements in need of further development.
Inference 1: LSG members needed to develop knowledge of how to use the graphing calculator as a means for efficiently comparing multiple representations and solution strategies
The first lesson implemented by the LSG involved solving systems of linear equations presented in word problems. The university faculty member reviewing the initial written lesson commented on the need to have students use the graphing calculator to make connections among the algebraic, tabular, and graphical representations of functions. Initially, the lesson called only for students to solve systems using their “preferred method.” The reviewers felt that using the calculator to make the connections among the representations would help students understand one solution strategy in terms of another and develop the capacity to make informed choices about which representation to use in solving a given problem.
In implementing the lesson, the LSG largely stayed with the idea of not pushing students beyond their individual preferred methods for solving systems of equations. During the debriefing session, they gave a variety of reasons for taking this course of action. The student population was cited as one contributing factor. Teachers noted that the class in which the lesson was implemented contained some special education students. They believed that the special education students would not be capable of understanding algebraic representations for the problems. Teachers also said that the standardized test given by the state did not require students to exhibit knowledge of multiple representations of functions – it required only that students generate a solution. Finally, time constraints of the lesson were cited as a reason not to delve into multiple representations. The school had shortened its class periods to 42 minutes, and the LSG felt that this did not provide adequate time to explore multiple representations of functions.
The LSG’s second lesson was written for an algebra class that contained only students who had been identified as academically strong. The main idea developed in the lesson was how to use the matrix multiplication capabilities of the graphing calculator to solve systems of equations. In reading the initial written lesson, reviewers again stated that using only one function on the calculator to produce an answer was not mathematically rich. In particular, they noted that the calculator was not used to compare and contrast representations and solution strategies for systems of equations.
Teachers again attributed this missing element of the lesson to lack of time during the class period and the types of questions students would have to answer on the state’s standardized test. Unlike the first lesson, however, student ability was not cited as one of the reasons for not delving into connections among multiple representations.
Comparing the first lesson to the second, the two entrenched reasons for not using the graphing calculator to make connections among representations and solution strategies were perceived time constraints and the fact that students would not be explicitly asked to make such comparisons on the state’s standardized test. This observation led to a hypothesis: Teachers needed a vision of how using the calculator to make comparisons among representations and solution strategies would ultimately be more time-efficient by helping build student understanding and, hence, student capacity to solve items on the state’s standardized test with a higher degree of success.
Sharing classroom activities with the potential to do so (e.g., Burke, Erickson, Lott, & Obert, 2001) thus became a goal for future work with the LSG. University faculty members reviewing the lesson also noted that understanding what a given representation shows about a system is valuable mathematically, regardless of whether or not it is explicitly stated on the guidelines for the state’s standardized test. Such “representational fluency” (Zbiek, Heid, Blume, & Dick, 2007) can be considered an important learning goal in and of itself.
Inference 2: LSG members needed to develop knowledge of how to avoid portraying graphing calculators as black boxes.
Although graphing calculators open up new learning experiences like the ability to generate and compare multiple representations efficiently, they also pose a pedagogical dilemma: When should students be allowed to use the technology, and when should they use paper and pencil? Buchberger (1989) posited a solution to this pedagogical dilemma by forwarding the White Box/Black Box Principle. The principle asserts that when an area of mathematics is new to students, hand calculations are important for building understanding of the concepts being studied. When the hand calculations become routine, and in some cases cumbersome, students should use the capabilities of the technology to facilitate problem-solving.
Doerr and Zangor (2000) posited a slightly different view of black box uses of calculators. They acknowledged that in some situations black box use was detrimental to helping students develop mathematical understanding, but also gave examples of classroom situations where students can use graphing calculators to make sense of mathematical concepts before doing hand computations. For instance, using calculators to test conjectures can lead to mathematically rich discussions when students are asked to compare calculator output to predicted results. Hence, the overall context of a lesson and its goals need to be taken into account in order to distinguish between potentially harmful and potentially productive “black box” uses of calculators.
Concerns about potentially harmful black box uses of technology arose in connection with the LSG’s second lesson. The lesson introduced the idea that matrices can be used to solve systems of equations. Students were to set up systems of equations for situations presented in word problems and put the systems in matrix form. The students were then told to “take the inverse of the first matrix and multiply it by the ‘answer’ matrix.” Finally, students were to use the calculator to determine the product of the two matrices. They were told that the product was the solution to the system of equations. So, for example, solving the system of equations 4x – 3y = 15; 8x + 2y = -10 was portrayed as consisting of the following sequence of steps:
- Step 1 – Write the system in matrix form:
![]()
- Step 2 – Compute the inverse of the first matrix by using the calculator:
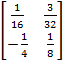
- Step 3 – Use the calculator to multiply the matrices:
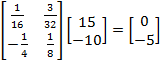 .
.
The solution to the system is (0, -5).
The appropriateness of this instructional sequence was discussed at length during the LSG’s debriefing session. One concern voiced by university faculty members was that students would not understand what the calculator was doing in performing matrix operations. University faculty conjectured that the instructional sequence could lead students to see the calculator merely as an answer-producing machine. Step 2 in the instructional sequence was seen as particularly problematic, since not all matrices are invertible. The graphing calculator returns an error message when one attempts to take the inverse of a noninvertible matrix.
A few students tried using the graphing calculator and matrices to solve systems that had no solution, and the calculator produced an error message because the corresponding matrices were not invertible. Students had no way of interpreting the error message based on the activities that took place during the lesson, because they had not carefully studied the meaning of the concept of inverse or matrix multiplication. The LSG teachers said that they planned to go back and help students interpret the “error” message in subsequent lessons. However, by not doing so in the given lesson, it seemed likely that they missed out on a teachable moment to help students reconcile the calculator output with their existing knowledge about systems of equations.
By treating the calculator as a black box during the matrix lesson, teachers also missed another opportunity to exploit the graphing calculator’s capabilities to generate multiple solution strategies and representations for comparison (as discussed in the exposition of Inference 1). The geometry of systems of equations was obscured by the black box approach. During the debriefing session, LSG teachers mentioned that in earlier lessons, they taught students that a unique solution for a system of two linear equations occurs when two lines intersect, the case of no solution corresponds to parallel lines, and the existence of infinitely many solutions indicates that the lines in the system are the same. However, these ideas were not related to the matrix representations in the matrix lesson.
Teachers did not have students explore the idea that when an inverse matrix exists, it corresponds precisely to having two lines that intersect at a single point. Likewise, there was no discussion of the fact that when the inverse does not exist, it indicates that the lines are parallel or the same. The original lesson plan contained a brief mention of the geometric interpretation of a system with one solution, but not of the other two cases. Reviewers expressed concern about this omission when reading the initial lesson, but the point had to be revisited during debriefing sessions because the original feedback was not utilized. Students could have used the calculator to graph the lines in cases where an inverse existed, as well as in cases where an inverse did not exist. Instructive comparisons could then have been drawn.
The LSG teachers affirmed the university faculty member’s concerns about the possibly premature black box usage of the graphing calculator for the lesson. However, they had difficulty seeing how they could move away from this sort of use of the calculator given their school context. On the state’s standardized tests, students were required to produce solutions to systems of equations. Teachers saw the matrix capabilities of the graphing calculator as a means to ensure that they would do so correctly. Understanding the mathematics of matrix operations, thus, became a distant secondary goal to producing correct answers to the systems of equations that would be included on the tests.
The LSG teachers acknowledged the possible harmful effects of having students learn a procedure without meaning, but at the same time were charged with having students produce correct answers to a narrow selection of systems of equations to be included on tests that would be used by administrators to judge the quality of their teaching. The matrix capabilities of the graphing calculator were thus seen by the teachers as a safe pathway for students to take to achieve high scores.
Although teachers seemed to see the matrix capabilities of the calculator as somewhat of a security blanket for students, near the end of the debriefing session, teachers paused to consider whether or not the matrix method, using the calculator, was even the best means for producing answers efficiently on the state test. The LSG was asked if students had experience with the substitution method for solving systems of equations before learning how to solve a system of equations on the graphing calculator. They replied that teachers had decided to take substitution out of the curriculum due to perceived time constraints in preparing students for the state test. This observation led to a discussion about systems of equations that could actually be solved more quickly, more accurately, and with more understanding using substitution rather than with matrices on the calculator (e.g., the system of equations y = 3x and y = x + 3).
This discussion appeared to help the LSG develop another important TPACK aspect – knowing how to foster students’ judicious use of technology by giving students situations where it would be inefficient to use the technology. Therefore, the debriefing session conversation illustrated how the LS-TPACK assessment method intertwines assessment with teacher education in “real time,” since teachers considered changes in practice at the same time their practice was assessed.
Inference 3: Teachers needed to develop knowledge of how to pose problems that expose the limitations of the graphing calculator.
Inference 3 is closely related to Inference 2, because students who develop only a “black box” view of technology may also come to trust the technology to produce answers for them even when it is not an appropriate tool to use for approaching a given problem. In both lessons, the LSG posed problems that were easily solved by the calculator with a minimum amount of human reasoning. In lesson 1, the solutions to the systems of equations were all viewable within the calculator’s standard window, so no estimation of the range of reasonable solutions to the systems was required. All of the problems in the lesson also had ordered pairs consisting of positive integers for their solutions, so students were not required to think about how algebraic approaches to systems with noninteger solutions yield exact answers, whereas graphical and tabular approaches generally do not. In Lesson 2, the LSG used only examples involving invertible matrices when showing how the matrix capabilities of the calculator could be used to solve systems of equations.
As discussed in connection with the previous two inferences, the state test and beliefs about students both appeared to be contributing factors to the LSG’s decision to pose problems requiring a minimum human element. The teachers felt that some students involved in lesson 1 were not capable of more advanced reasoning about systems of equations and also felt that students could succeed on the state test by following a sequence of steps on the calculator without thinking much about them.
In the four-column lesson plan for Lesson 2, many of the remarks in the “student’s anticipated responses” column pertained to students’ procedural understanding of carrying out steps on the calculator (e.g., “Some students will need help with putting matrices into the calculator,” and “Some students will want to skip steps in the process so they do not have to write as much”). Helping the LSG move beyond posing straightforward problems solvable solely with well-defined sequences of calculator steps, hence, emerged as perhaps the most challenging goal for future work with the group, since beliefs about students and test-related contextual factors both worked against attainment of the goal.
Reflections on Strengths and Weaknesses of the Assessment Framework
One’s perceptions of the strengths and weaknesses of the LS-TPACK assessment model will depend, in part, on his or her philosophical orientation toward assessment. Some aspects of the model considered strengths by those working within a qualitative, “accounts of practice” type of paradigm may be considered weaknesses by those who use quantitative, psychometric methods. However, there are also some strengths and weaknesses that are somewhat philosophically neutral and likely not as dependent on one’s assessment paradigm.
From assessment perspectives in the tradition of the accounts of practice paradigm, the manner in which the LS-TPACK model intertwines assessment with professional development could be considered one of its strengths. Using this approach eliminates the need for developing the assessment component of a project separately from the teaching component. This, in turn, has the potential to save time and resources. By writing lesson reviews and participating in debriefing sessions, university faculty members simultaneously assess teachers’ knowledge and provide professional development.
Reviews and comments during debriefing sessions are not simply for the purpose of summative assessment, but also to identify aspects of teachers’ lessons that can be improved upon. University faculty members’ assessments of teachers’ lessons are essentially “reviews that teach” (Smith, 2004), so they provide teachers with the same sort of learning opportunities that university faculty experience when submitting their research for peer review.
The intertwinement of assessment and professional development could also be considered a weakness, particularly from a psychometric perspective. Psychometrically sound items are costly to develop. Therefore, the items themselves and teachers’ performance data are generally not shared with the teachers completing them. Doing so could lead to inaccurate measurements of the construct under investigation, because increases in scores could then be plausibly attributed to teachers’ enhanced test-taking skills rather than increases in their knowledge related to the construct of interest. Transferring this line of reasoning to the LS-TPACK model might lead one to the conclusion that increases in teachers’ observed LS-TPACK could be attributed to increased ability to write lessons that please the reviewer, since the teachers have access to the reviewers’ comments throughout the entire process.
The concern that teachers’ knowledge of reviewers’ tendencies clouds the portrait of TPACK ultimately constructed for them is mitigated by several features of the LS-TPACK model. The model is based on assessment of knowledge enacted in the context of teaching lessons. Teachers not only write lessons, but must implement them with students in their school. Shifts in lesson writing that are made solely in order to accommodate reviewers are likely to be apparent in students’ reactions to lessons. The debriefing sessions provide an opportunity to inquire about sources of unusual student behavior.
In addition, teachers have little incentive for making unusual shifts in instructional practices, as they are explicitly told that they should use their knowledge of the school context to decide which pieces of reviewer feedback to implement and which pieces cannot be feasibly implemented. They are not required to implement reviewers’ advice to remain part of the project. Therefore, documented shifts in TPACK are likely to be the result of genuine teacher learning rather than merely attempts to receive more favorable reviews.
Researchers embracing a psychometric assessment paradigm might also consider the LS-TPACK model to be deficient in that it does not provide a way to measure individual teachers’ knowledge. The very nature of the process, which intertwines professional development and assessment of TPACK, provides several opportunities for teachers to influence one another in the way they respond to assessment questions. Given this situation, it becomes virtually impossible to draw inferences about an individual teacher’s knowledge in isolation from the collective LSG.
Although measurement of individual teachers’ knowledge is not feasible within the LS-TPACK model, its ability to capture the reasoning of groups of teachers makes it an assessment model worthy of consideration. It is increasingly recognized that communities of practice (Lave & Wenger, 1991), such as lesson study groups, are powerful learning sites for teachers. Such communities allow teachers to develop knowledge in the context of their teaching practice. Professional development projects that seek to foster communities of practice need ways to capture the fluid, dynamic development of knowledge that takes place in the community. The LS-TPACK model provides a means for doing so, because it focuses on documenting, examining, and explaining the interactions that take place among LSG members.
In contrast, the customary psychometric goal is to produce snapshots of individual teachers’ knowledge at fixed moments in time. Of course, for some professional development projects, individual snapshots of teachers’ knowledge may be desired. In such cases, psychometrically sound items can be used to supplement the LS-TPACK assessment, possibly in pre- and postassessments, without foreseeable adverse consequences to the integrity of either assessment method.
Even if one holds a purely psychometric assessment paradigm, the LS-TPACK model can be seen as valuable because of its exploratory potential. The construct of TPACK itself is relatively new among the types of teacher knowledge needing assessment. From a psychometric perspective, the in-depth exploration of specific cases and examples can help further define and clarify emergent constructs (American Statistical Association, 2007). Unanticipated and potentially important aspects of the TPACK construct can be uncovered as actual teaching practice is observed, documented, and evaluated.
Qualitative “exploratory” studies can also be valued for their potential to generate plausible ideas for assessment items to be field tested for their psychometric properties (Rossi, Wright, & Anderson, 1983). For example, the first inference drawn about teachers’ knowledge in this paper might motivate the formation of items that measure teachers’ knowledge of using the graphing calculator to facilitate the exploration of multiple representations and solution strategies for systems of equations.
On the other hand, from the accounts-of-practice perspective, the exploration that occurs as part of the LS-TPACK model can be considered valuable as an end in itself, because it captures the fluid, contextually situated, and collective development of teachers’ knowledge. The dynamic models of teachers’ TPACK and explanations for its growth or stasis can be seen as ends in themselves rather than a means for attempting to produce quantitative measurements.
From either perspective, however, the in-depth exploration inherent to the model can be perceived as one of its strengths. The reason for viewing the exploratory nature of LS-TPACK as a strength will depend largely on one’s beliefs about the nature of knowledge. If one holds that knowledge is an individual characteristic that can be precisely measured with instruments that do not need to take teachers’ instructional contexts into account, the exploratory aspect is valuable only insofar as it leads to the development of psychometrically sound assessment items. If one holds that teachers’ knowledge development is contextually situated and fluid, then the exploratory nature of LS-TPACK offers a more authentic way to track teachers’ learning trajectories (Peressini, Borko, Romagnano, Knuth, & Willis, 2004) than more static, context-independent psychometric approaches.
Another pragmatic aspect of the LS-TPACK model that can be viewed from different assessment paradigms as a strength is that it is adaptable to the assessment of TPACK in many different settings. Lesson study has been used as a professional development strategy in other content areas, such as science (Kolenda, 2007) and language arts (Lewis, 2002). Practicing teachers from the elementary (Lewis, Perry, Hurd, & O’Connell, 2006) to the college level (Alvine, Judson, Schein, & Yoshida, 2007; Roback, Legler, Chance, & Moore, 2006) can benefit from engaging in the process. Lesson study can also be adapted for use with preservice teachers (Marble, 2007), so the LS-TPACK model need not be limited solely to the assessment of in-service education for high school mathematics teachers. The data gathering and analysis process inherent to the LS-TPACK model dovetails with the lesson study process, making it an assessment approach that is portable to a variety of settings.
A final strength of the LS-TPACK model worthy of mention, from the perspective of virtually any assessment paradigm, is that it draws upon the expertise of mathematicians, mathematics educators, and teachers. Each group of individuals brings unique perspectives to the reviews they complete and the debriefing sessions they attend. Mathematicians generally bring a content-oriented perspective that concentrates upon the fidelity of the lesson to the discipline of mathematics. Mathematics educators are often in a position to comment on the psychological and developmental appropriateness of lessons. In the project described in this paper, mathematicians and mathematics educators were able to couple their knowledge of content and students with knowledge of technology, since they had previously taught the algebraic topics under consideration with the graphing calculator. University faculty members with this knowledge were purposefully chosen to participate in the project.
Without previous experience using technology to teach the concepts under consideration, it seems unlikely they would have been able to contribute meaningfully to the assessment of TPACK. Teachers play a valuable role in the assessment process as well, since they help to situate the lesson within the overall curriculum and school setting, helping to prevent university faculty from drawing errant or superficial inferences from their observations.
Thoughts on Getting Started With the LS-TPACK Model
Researchers who consider LS-TPACK to be a viable means of assessing teacher knowledge need to devise strategies to overcome some logistical challenges. Establishing productive LSGs in schools is perhaps the foremost of these challenges. For the project described in this paper, the decision to use lesson study as a professional development model was agreed upon during discussions with teacher and administrator representatives. Teachers in the school district from which the examples in this paper came were not required to participate, but all of them did so after learning about the lesson study model. Teachers received stipends for time spent in lesson planning and debriefing sessions. They also received expense accounts for purchasing the instructional materials and technology required to carry out the LSG-planned lessons. Educating teachers on the lesson study model, giving them the choice of whether or not to participate, and providing monetary support for those who chose to participate were, therefore, all key elements in attracting teachers to LSG participation.
A second major logistical challenge in implementing LS-TPACK is recruiting university faculty. The university faculty members in the project described in this paper all had a stake in teacher education. Some of them taught courses in the mathematics major that were taken by prospective secondary teachers, and others taught mathematics content or methods designed specifically for preservice elementary and middle school teachers. As teachers submitted written lessons to the university, the third author looked for matches between the content of the lesson and the teaching and research interests of university faculty members.
Faculty members were then asked to participate based on the match between their interests and the interests of the LSG. They were informed that writing a lesson review according to the guidelines in Figure 3 would constitute approximately 1 day’s work (usually spread over several days), and that preparing for and participating in a debriefing session would take about the same amount of time. Reimbursement was then offered in accord with these time requirements. This process facilitated the construction of an efficient communication mechanism between the university and the LSG.
Once faculty members have been recruited as reviewers, discussion about the nature of TPACK can help inform the feedback they give to teachers on using technology. During such discussions, it is important to keep in mind that TPACK is an evolving construct, and that it is likely premature and counterproductive to try to pin down a final definition for it. Shulman’s (1987) original formulation of “pedagogical content knowledge” is still being debated, revised, and extended (Hill et al., 2008), so formulations of TPACK will likely remain in flux for some time.
A somewhat concrete aspect of TPACK, however, is that it is related to the three-way intersection of technology, pedagogy, and content (Koehler & Mishra, 2008). The three-way intersection idea can help inform the assessment team’s initial thinking, even though there may be debate about the nature of the three aspects. Zbiek et al., (2007) provided a helpful discussion of some specific constructs that may be related to TPACK. These included ideas like representational fluency (including use of multiple representations, hotlinks, and interactive displays) and mathematical concordance (i.e., examining the alignment between technology-generated representations and mathematical ones). Even though the formal definition and formulation of TPACK remains in flux, focusing on these constructs in lessons can help get the assessment team started. In the process, possible new aspects of TPACK may become apparent as well.
Another important consideration for the assessment team is to avoid a purely deficit-oriented approach to describing teachers’ TPACK. Although it can be useful to identify areas of TPACK that need development, as illustrated in this paper, it is also important to identify teachers’ strengths when they are apparent. Some strengths are implicit in the examples given earlier. For example, even though teachers did not use the graphing calculator’s representation-generating capabilities to its fullest extent, they knew the mechanics of generating various representations on the calculator. This baseline knowledge is an important prerequisite to learning to use the graphing calculator more effectively in the classroom. Also, even though they used the matrix capabilities of the calculator in a manner that could be detrimental to students’ learning, they later acknowledged the problems that this teaching strategy could cause. This bit of knowledge sparked consideration of how to navigate the complex and shifting dynamics among high stakes testing requirements, technology usage, and students’ learning more effectively. By acknowledging strong aspects of teachers’ TPACK along with weak ones, university faculty can take inventory of the knowledge teachers possess and identify viable directions to pursue in future work with them.
Conclusion
The concepts of lesson study and TPACK are both relatively new to the field of teacher education. Both are increasingly becoming recognized as important elements of the field. This article connects the two concepts by demonstrating that lesson study is not only an emerging approach to teacher education, but also the foundation for a potentially robust method for assessing the nature of teachers’ TPACK. The LS-TPACK model provides a means for assessing the TPACK exhibited by groups of teachers as they immerse themselves in the simultaneous study of content, technology, and pedagogy.
References
Alagic, M., & Palenz, D. (2006). Teachers explore linear and exponential growth: Spreadsheets as cognitive tools. Journal of Technology and Teacher Education, 14, 633-649.
Alvine, A., Judson, T.W., Schein, M., & Yoshida, T. (2007). What graduate students (and the rest of us) can learn from lesson study. College Teaching, 55(3), 109-113.
American Statistical Association. (2007). Using statistics effectively in mathematics education research. Retrieved from http://www.amstat.org/education/pdfs/UsingStatisticsEffectivelyinMathEdResearch.pdf
Buchberger, B. (1989). Should students learn integration rules? SIGSAM Bulletin, 24(1), 10-17.
Burke, M., Erickson, D., Lott, J.W., & Obert, M. (2001). Navigating through algebra in grades 9-12. Reston, VA: National Council of Teachers of Mathematics.
Cobb, P. (2000). Conducting teaching experiments in collaboration with teachers. In A.E. Kelly & R. Lesh (Eds.), Handbook of research design in mathematics and science education (pp. 307-333). Hillsdale, NJ: Lawrence Erlbaum Associates.
Curcio, F. (2002). A user’s guide to Japanese lesson study: Ideas for improving mathematics teaching. Reston, VA: National Council of Teachers of Mathematics.
Doerr, H., & Zangor, R. (2000). Creating meaning for and with the graphing calculator. Educational Studies in Mathematics, 41, 143-163.
Fernandez, C. (2005). Exploring lesson study in teacher preparation. In H.L., Chick & J.L.,Vincent (Eds.), Proceedings of the 29th conference of the International Group for the Psychology of Mathematics Education, Vol. 2 (pp. 305-312). Melbourne: PME.
Fey, J.T. (1989). Technology and mathematics education: A survey of recent developments and important problems. Educational Studies in Mathematics, 20, 237-272.
Finzer, W. (2002). Fathom [software]. Emeryville, CA: Key Curriculum Press.
Groth, R.E. (2008). Analyzing online discourse to assess students’ thinking. Mathematics Teacher, 101, 422-427.
Hiebert, J., & Stigler, J.W. (2000). A proposal for improving classroom teaching: Lessons from the TIMSS video study. Elementary School Journal, 101, 3-20.
Hill, H.C., Ball, D.L., & Schilling, S.G. (2008). Unpacking pedagogical content knowledge: Conceptualizing and measuring teachers’ topic-specific knowledge of students. Journal for Research in Mathematics Education, 39, 372-400.
Hill, H.C., Schilling, S.G., & Ball, D.L. (2004). Developing measures of teachers’ mathematics knowledge for teaching. Elementary School Journal, 105, 11-30.
Jackiw, N. (2001). The Geometer’s Sketchpad. Berkeley, CA: Key Curriculum Press.
Koehler, M.J., & Mishra, P. (2008). Introducing TPCK. In AACTE Committee on Innovation and Technology (Ed.), Handbook of technological pedagogical content knowledge (TPCK) for educators (pp. 3-29). New York: Routledge.
Kolenda, R.L. (2007). Japanese lesson study, staff development, and science education reform – The Neshaminy story. Science Educator, 16(1), 29-33.
Lave, J., & Wenger, E. (1991). Situated learning: Legitimate peripheral participation. New York: Cambridge University Press.
Lee, H.S., & Hollebrands, K.F. (2008). Preparing to teach data analysis and probability with technology. In C. Batanero, G. Burrill, C. Reading, & A. Rossman (Eds.), Joint ICMI/IASE study: Teaching statistics in school mathematics. Challenges for teaching and teacher education. Proceedings of the ICMI Study 18 and 2008 IASE Round Table Conference. Retrieved from http://www.ugr.es/~icmi/iase_study/
Lewis, C. (2002). Lesson study: A handbook of teacher-led instructional change. Philadelphia: Research for Better Schools.
Lewis, C., Perry, R., Hurd, J., & O’Connell, M.P. (2006). Lesson study comes of age in North America. Phi Delta Kappan, 88, 273-281.
Lewis, C., & Tsuchida, I. (1998 Winter). A lesson is like a swiftly flowing river: How research lessons improve Japanese education. American Educator, 14-17, 50-52.
Marble, S. (2007). Inquiry into teaching: Lesson study in elementary science methods. Journal of Science Teacher Education, 18, 935-953.
National Council of Teachers of Mathematics and National Council for Accreditation of Teacher Education. (2005). NCATE/NCTM program standards: Programs for the initial preparation of mathematics teachers. Reston, VA: National Council of Teachers of Mathematics.
Peressini, D., Borko, H., Romagnano, L., Knuth, E., & Willis, C. (2004). A conceptual framework for learning to teach secondary mathematics: A situative perspective. Educational Studies in Mathematics, 56, 67-96.
Reece, G.C., Dick, J., Dildine, J.P., Smith, K., Storaasli, M., Travers, J.K., Wotal, S., & Zygas, D. (2005). Engaging students in authentic mathematics activities through calculators and small robots. In W.J. Masalski & P.C. Elliot (Eds.), Technology-supported mathematics learning environments: The Sixty-Seventh Yearbook of the National Council of Teachers of Mathematics (pp. 319-344). Reston, VA: National Council of Teachers of Mathematics.
Roback, P., Chance, B., Legler, J., & Moore, T. (2006). Applying Japanese lesson study principles to an upper-level undergraduate statistics course. Journal of Statistics Education, 14(2). Retrieved from http://www.amstat.org/publications/jse/v14n2/roback.html
Rossi, P.H., Wright, J.D., & Anderson, A.B. (Eds.). (1983). Handbook of survey research. New York, NY: Academic Press.
Shulman, L.S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57, 1-22.
Simon, M.A., & Tzur, R. (1999). Explicating the teacher’s perspective from the researchers’ perspectives: Generating accounts of mathematics teachers’ practice. Journal for Research in Mathematics Education, 30, 252-264.
Smith, J.P. (2004). Reviews that teach. Journal for Research in Mathematics Education, 35, 292-296.
Stigler, J.W., & Hiebert, J. (1999). The teaching gap: Best ideas from the world’s teachers for improving education in the classroom. New York, NY: Free Press.
Yin, R.K. (2003). Case study research: Design and methods (3rd ed.). Thousand Oaks, CA: Sage.
Zbiek, R.M., Heid, K.M., Blume, G.W., & Dick, T.P. (2007). Research on technology in mathematics education: A perspective of constructs. In F.K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 1169-1207). Charlotte, NC: Information Age Publishing & National Council of Teachers of Mathematics.
Author Notes:
Preparation of this article was supported by mathematics partnership grant funds from the Delaware Department of Education.
Randall Groth
Salisbury University
email: [email protected]
Donald Spickler
Salisbury University
email: [email protected]
Jennifer Bergner
Salisbury University
email: [email protected]
Michael Bardzell
Salisbury University
email: [email protected]
![]()