During the past decades, computers have been used as learning tools in education. Computer-assisted instruction (CAI) provided a better learning environment in education (Chang, Sung, & Lin, 2006; Crook, 1994; Li & Edmonds, 2005; Liao, 2007; Lin, 2008; Niewiec & Walberg, 1987; Ragasa, 2008). At present, the dynamic and interactive Web sites related to mathematics teaching and learning can be easily reached through the Internet.
In England, the National Curriculum for England (2008) encouraged teaching mathematics by using information and communication technology. In the USA, the National Council of Teachers of Mathematics’ (NCTM, 2000) Principles and Standards for School Mathematics encouraged teachers to use computers in the classroom and stated, “Computers are essential tools for teaching, learning, and doing mathematics. They furnish visual images of mathematical ideas, they facilitate organizing and analyzing data, and they compute efficiently and accurately” (p. 24).
Despite the National Curriculum for England and the NCTM standards’ support for using computers in the classroom, the empirical research conducted on the comparative efficiency of Web-based instruction (WBI) and traditional instruction in mathematics teacher education is limited. However, studies of how CAI programs compare to other methods of teaching have been conducted since the 1980s. Mevarech and Rich (1985) compared the effects of CAI and traditional instruction on the mathematics achievement and attitudes of disadvantaged Israeli students in grades 3, 4, and 5. The results indicated that students in the CAI group scored higher on achievement. In addition, their attitudes toward school and toward themselves as mathematics learners were more positive.
Ganguli (1992) investigated the effect on students’ attitudes of the computer as a teaching aid. Fifty-one students participated in an experimental group that involved a computer as an aid in teaching mathematical concepts. Fifty-nine students in a control group were taught traditional methods. The results indicated a significant treatment effect on students’ attitudes, favoring the use of a computer as a teaching aid.
Tilidetzke (1992) investigated differences in achievement for control groups learning college algebra using traditional classroom instruction methods, compared to experimental groups using computer algebra tutorials for three precalculus topics. The results indicated no significant difference in mean scores on a posttest or a delayed posttest between CAI and traditional instruction in a college algebra course when studying three topics of course material with 2 hours of computer lab time.
Ragasa (2008) compared the effects of 38 sophomore college students in the basic statistics taught with the use of CAI and 15 students with the use of the traditional method on the basic statistics achievement. The results indicated a significant treatment effect on students’ achievement posttest.
Research on the importance of CAI on PK-12 students has examined the effectiveness of CAI on student achievement (Chen & Liu, 2007; Liao, 2007), including drill-and-practice (Fuchs, Fuchs, Hamlet, & Powell, 2006), tutorial (Donovan & Nakhleh, 2007; Hannafin, Burruss, & Little, 2001), and simulation (Iskander & Curtis, 2005; Schorr & Goldin, 2008). The findings of the effectiveness of CAI on achievement suggest that CAI is more effective than traditional instruction. They show that CAI improved student mathematics performance and attitude (Chen & Liu, 2007; Liao, 2007).
Research studies have found that CAI improves instruction for PK-12 students because students receive immediate feedback, and the programs let students know whether their answer is correct. CAI moves at the students’ pace and usually does not move ahead until they have mastered the skill (Fuchs, Fuchs, Hamlett, & Appleton, 2002; Fuchs et al., 2006).
Based on the study of drill-and-practice, Fuchs et al. (2006) found that CAI improved number combination skills among children with concurrent risk for mathematics disability and reading disability. Iskander and Curtis (2005) and Schorr and Goldin (2008) investigated CAI simulations on mathematics learning. They found that CAI helps to capture the students’ attention, because the programs are interactive and learner centered. It is focused on the learner rather than the teacher and on learner active mastery of material through interactive learning and teaching.
Research has shown that effective use of multimedia or interactive Web-based modules can increase student learning (Aberson, Berger, Healy, & Romero, 2003; Bliwise, 2005; Fletcher-Flinn & Gravatt, 1995; McNeil & Nelson, 1991). Aberson et al. (2003) evaluated a Web-based interactive tutorial used to present hypothesis testing concepts. The results indicated that students who used the tutorial performed better on a quiz than did students who completed the standard laboratory, supporting the effectiveness of this freely available online tutorial. Similarly, Bliwise (2005) suggested that a Web-based tutorial improved student learning on statistics.
Several research studies have found that preservice elementary teachers have difficulties with the concepts of fractions (Ball, 1990; Behr, Khoury, Harel, Post, & Lesh, 1997; Cramer, Post, & del Mas, 2002; Davis & Thipkong, 1991; Flores, 2002; Izsak, 2008; Ma, 1999; Rizvi & Lawson, 2007; Simon, 1993; Tirosh, 2000). Ball (1990) found that preservice elementary teachers had significant difficulty with the meaning of division of fractions. Similarly, in a study of the prospective elementary teachers’ knowledge of division, Simon (1993) concluded that preservice elementary teachers have a serious shortcoming in their understanding of division by modeling of situations. The preservice elementary teachers were unable to think flexibly and consciously about division as partitive and quotitive.
Research suggests that preservice elementary teachers experience difficulty in explaining fractions to children and are unable to explain why algorithms work (Chinnappan, 2000; Selden & Selden, 1997). Similarly, Tirosh (2000) found that before the mathematics methods course most participants knew how to divide fractions but could not explain the procedure. In addition, they were unaware of major sources of students’ incorrect responses in fraction division. In the study of prospective teachers’ knowledge of the concept of division, Rizvi and Lawson (2007) discovered that the prospective teachers successfully represented division of whole numbers using models of fair sharing and, to a lesser extent, repeated subtraction. However, they had difficulty in successfully representing division of fractions.
Several research studies have found a positive correlation between teachers’ content knowledge and their students’ success in learning mathematics (Darling-Hammond, 1999; Hill, Rowan, & Ball, 2005; Hill, Schilling, & Ball, 2004). In addition, research has demonstrated a connection between teachers’ pedagogical knowledge and students’ performance (Carpenter, Fennema, Peterson, & Carey, 1988; Rowan, Chiang, & Miller, 1997; Staub & Stern, 2002).
Therefore, in order to teach effectively in an elementary school, a teacher needs not only a strong background in mathematics but also a thorough understanding of pedagogy. A competent teacher should have a solid foundation of both procedural knowledge and conceptual knowledge. This type of knowledge is known as knowledge of mathematics for teaching (Ball, 1990; Hill et al., 2005) and as profound understanding of fundamental mathematics (Ma, 1999). That is, teachers need a deeper, more profound understanding of fundamental mathematics.
Hiebert and Lefevre (1986) described “procedural knowledge as being made up of two distinct parts. One part is composed of the formal language, or symbol representation system, of mathematics. The other part consists of the algorithms, or rules, for completing mathematical tasks” (p. 5). Procedural knowledge includes algorithms and formulas used to solve mathematical problems. Procedure knowledge is knowing how to (Hiebert & Lefevre, 1986). For example, students who know how to apply the rule to do fraction division are exhibiting procedural knowledge.
Hiebert and Lefevre further defined conceptual knowledge as being characterized most clearly as knowledge that is rich in relationships. It can be thought of as a connected web of knowledge, a network in which the linking relationships are as prominent as the discrete pieces of information. Relationships pervade the individual facts and propositions so that all pieces of information are linked to some network (p. 3). Thus, conceptual knowledge provides the reasons why these formulas work. Conceptual knowledge is knowing why (Hiebert & Lefevre, 1986). For example, if students know why they “invert and multiply” in fraction division, they are exhibiting conceptual knowledge.
Teaching for procedural knowledge means teaching students to solve a problem through the manipulation of mathematical skills, such as procedures, rules, formulas, algorithms, and symbols used in mathematics (Skemp, 1987). Teaching for conceptual knowledge, on the other hand, means to teach students to understand mathematical concepts by being able to interpret and apply them correctly to a variety of situations, as well as to translate these concepts between verbal statements and their equivalent mathematical expressions (Skemp, 1987). In addition, students make connections to what they already know, thus allowing them to extend their prior knowledge and transfer it to new situations (National Council of Teachers of Mathematics, 2000).
Ma (1999) described profound understanding of fundamental mathematics (PUFM) in her book Knowing and Teaching Elementary Mathematics. PUFM provides a vision of the ideal structure of elementary teachers’ conceptual and procedural knowledge. She found that some classroom teachers lacked conceptual knowledge and others did not. She compared conceptual understanding and procedural knowledge of experienced U.S. and Chinese primary teachers across a range of mathematical topics. For example, she asked teachers to calculate 1¾ ÷ ½. She found that only 43% of the U.S. teachers succeeded in calculation, and none of them showed an understanding of the rationale of the algorithm. In contrast, all Chinese teachers succeeded in their calculations. In addition, many teachers showed various calculation methods and evaluated them, and they also demonstrated their conceptual understanding.
To further examine how preservice teachers develop their understanding of fraction division, I investigated the comparative efficiency of WBI and traditional teaching methods on their fraction knowledge. The analysis focuses on a fraction topic with which most people have difficulty. I attempted to understand which method is better for preservice teachers in procedural and conceptual knowledge for learning fractions.
Purpose of the Study
The purpose of this study was to compare the effectiveness of web-based and traditional instruction on preservice elementary teachers’ procedural knowledge and their conceptual knowledge of fractions. The specific questions investigated in the study were as follows:
- What is the effect of WBI on students’ procedural knowledge on posttest scores when their pretest scores were used as a covariate?
- What is the difference in students’ procedural knowledge in eight areas of fraction concepts on posttest scores in the experimental and control groups?
- What is the effect of WBI on students’ conceptual knowledge on posttest scores when their pretest scores were used as a covariate?
- What is the difference in students’ conceptual knowledge of eight areas of fraction concepts on posttest scores in the experimental and control groups?
Method
Subjects
The subjects of this study were 42 university students (aged 18 to 21; M = 19.20, SD = 0.25) attending two classes in a College of Education. Ninety-five percent of the participants were female (40 women, 2 men). The minimum number of math courses required by the university is four. All the participants were in a teacher education program, having completed two required prerequisite courses. The Mathematics Content and Methods for the Elementary School course is a 3-hour lecture per week and a required course for all undergraduate students in the teacher education program. The fraction unit was covered during the fall semester. One class was randomly assigned to the experimental group (n = 21), while the other class formed the control group (n = 21). The students in the experimental group were taught with Web-based resources related to fraction concepts, while the students in the control group received traditional instruction. All students were taught by the same instructor, and both groups received 6 weeks of instruction, or 18 hours, in the study.
Instrument
The test on fraction concepts was adapted from Cramer et al. (2002) and Ma (1999). I modified this test to provide more emphasis on procedural and conceptual knowledge. The survey instruments were piloted with 40 preservice teachers who were enrolled in different mathematics methods courses. A panel of specialists, including three mathematics educators, ascertained content validity of the test. The survey instruments were modified following their suggestions (see appendix).
Thirty-two test items were used as both pretest and posttest measures of students’ learning of fraction concepts. The test was specifically designed to measure possible fraction concepts in areas related to
- Concepts: items 1, 2, 3, and 4
- Equivalence: items 5, 6, 7, and 8
- Order: items 9, 10, 11, and 12
- Fraction addition: items 13, 14, 15, and 16
- Fraction subtraction: items 17, 18, 19, and 20
- Fraction multiplication: items 21, 22, 23, and 24
- Fraction division: items 25, 26, 27, and 28
- Transfer: items 29, 30, 31, and 32.
The procedural knowledge items were items 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, and 31. The conceptual knowledge items are items were 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, and 32. The internal reliability (Cronbach’s alpha) of the test was found to be 0.86 in this study. The following two items exemplify respective items included on the test.
1. Procedural knowledge item:
Solve the problem
![]() = ?
= ?
2. Conceptual knowledge item:
Imagine that you are teaching multiplication with fractions. To make this meaningful for kids, what would you say would be a good story or model for
![]() = ?
= ?
Treatment
There were two groups of students: one experimental group and one control group. Both groups received 6 weeks of instruction on the fractions units (18 hours). Topics related to fraction concepts were covered as part of the regular classroom curriculum in Mathematics Content and Methods for the Elementary School course. The topics were fraction concepts, equivalence of fraction, order of fractions, fraction operations, and transfer.
Students in the experimental group received instruction using Internet computer applets on the mathematics content. They spent all of their classtime using WBI. When first developed, two mathematics education experts selected and reviewed Web sites that were comprehensive, well-organized, dynamic, interactive, hands-on, and ready to use for mathematics teaching in the classroom. For example, interactive Web sites, including the National Library of Virtual Manipulatives (http://nlvm.usu.edu/), Illuminations (http://illuminations.nctm.org/; see Figure 1) and Visual Fractions (http://www.visualfractions.com; see Figure 2) were selected.
Figure 1. Examples of the interactive Web sites.

Figure 2. Sample page that provides immediate feedback.
Interactive WBI was developed, as research suggests that animated demonstration may be more efficiently processed by learners than nonanimated demonstration (Wender & Muehlboeck, 2003). Therefore, students in the experimental group had tasks making use of dynamic animated representations on computers.
The selected Internet computer applets are interactive and can illustrate a concept through attractive animation, sound, and demonstration. In addition, they allow students to progress at their own pace and to work individually or to problem solve in a group. They provide immediate feedback, letting students know whether their answers are correct. If an answer is not correct, the program shows students how to answer the question correctly, and this helps them strengthen their procedural knowledge of fractions (see Figure 2). For the conceptual knowledge of fractions, they could find many solutions (Becker & Shimada, 1997; Hashimoto & Becker, 1999) to a problem like ½ ÷ ¾ on the Internet. In addition, they could find a story or a meaning to explain a problem like ½ ÷ ¾ on the Internet computer programs.
Students in the control group were instructed with traditional instruction. The traditional instruction method in this study was lectures given by a teacher, use of textbooks and other materials, and a clear explanation of procedural knowledge and conceptual knowledge of fractions to students. The teacher demonstrated fraction models and a review of the textbook topics. They spent their class time using hands-on and manipulatives activities. However, they did not have any tasks that made use of dynamic representations on computers (see Table 1).
Table 1
Web-based Instruction vs. Traditional Instruction
Method | Web-based Instruction | Traditional Instruction |
| Instructional content | The instruction included lessons on fraction concepts, equivalence of fraction, order of fractions, fraction operations, and transfer. | The instruction included lessons on fraction concepts, equivalence of fraction, order of fractions, fraction operations, and transfer. |
| Forms of instruction | The students worked in pairs on a computer. | The students worked in groups without using any computers. |
| Learning environments | Student received instruction using a computer-based, online learning system. | Students did not use any computer-assisted instructional programs or software. |
| Homework assignments | The students completed a series of homework assignments on a computer | The students completed a series of homework assignments without using any computers. |
Analysis of Data
To understand how the two groups would be affected by the treatment in terms of students’ procedural and conceptual knowledge, an analysis of covariance (ANCOVA) on posttest scores with the pretest as the covariate on the procedural and conceptual knowledge items was conducted to determine significance between them. Students were given 1 point for the correct answer; otherwise, no credit was given.
For research questions 1 and 3, an ANCOVA was used to determine the treatment effects on students’ procedural and conceptual knowledge, respectively, when pretest results were used as a covariate. For research questions 2, an analysis of variance (ANOVA) was used to identify students’ procedural knowledge in areas of fraction concepts and whether there was a significant difference on posttest results between the experimental and control group students’ correct answers. For research question 4, ANOVA was used to identify students’ conceptual knowledge of eight areas of fraction concepts, and whether or not there was a significant difference on posttest results between the experimental and control group students’ conceptual understanding.
Results
Table 2 shows the students’ mean and standard deviations for pre- and posttest scores for procedural knowledge and pre- and posttest scores for conceptual knowledge responses for the experimental and the control groups. Students in the experimental group had higher performance in procedural knowledge and conceptual knowledge on post-Fraction Knowledge Test (FKT) scores than did the students in the control group (see Figure 3). In order to identify students’ prior knowledge in fraction concepts, the FKT was administered to the experimental and control groups before treatment. Analysis of independent t-test results showed no significant mean difference between the groups, t (40) = 1.697, p > 0.05. After the treatment, the ANCOVA was run to compare the effects of instruction on students’ fraction concepts on post-FKT scores for procedural knowledge and conceptual knowledge responses when their pre-FKT scores were used as a covariate.
Table 2
Means, Standard Deviation (SD), and Effect Size for Pre- and Post-FKT Scores
Test | Group | n | M | SD | Effect Size |
| PK | |||||
| Pre-FKT | Experimental | 21 | 11.76 | 3.05 | |
| Control | 21 | 11.11 | 3.28 | ||
| Post-FKT | Experimental | 21 | 15.34 | 1.3 | |
| Control | 21 | 13.22 | 2.2 | 0.81 | |
| CK | |||||
| Pre-FKT | Experimental | 21 | 5.19 | 3.21 | |
| Control | 21 | 4.72 | 3.00 | ||
| Post-FKT | Experimental | 21 | 11.25 | 2.44 | |
| Control | 21 | 6.66 | 2.13 | 1.80 | |
| PK: procedural knowledge; CK: conceptual knowledge; FKT: Fraction Knowledge Test | |||||
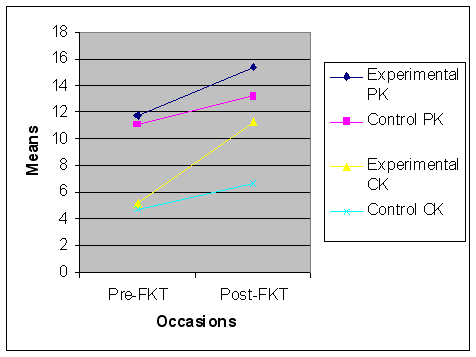
Figure 3. Pretest and posttest for procedural and conceptual knowledge scores.
Tables 3 and 4 provide the summary of ANCOVA comparing the mean scores of the students’ fraction concepts in experimental and control groups with respect to post-FKT scores for procedural knowledge and conceptual knowledge responses, respectively. The results of ANCOVA showed a significant difference between the experimental and control groups with respect to students’ procedural knowledge, F(1, 39) = 12.69, p < 0.05, and conceptual knowledge, F(1, 39) = 64.63, p < 0.05. The students in the experimental group, who were taught with WBI, demonstrated better performance in fraction concepts than did the control group students, who received traditional instruction.
Table 3
Summary of Analysis of Covariance Comparing the Mean Post-FKT Scores of Students’ Procedural Knowledge in the Experimental and the Control Groups
Source | Type III Sum of Squares | df | Mean Square | F | Sig. |
| Pretest | 40.642 | 1 | 40.642 | 19.308 | .001 |
| Group | 26.715 | 1 | 26.715 | 12.691 | .001 |
| Error | 82.094 | 39 | 2.105 | ||
| *p < 0.05 | |||||
Table 4
Summary of Analysis of Covariance Comparing the Mean Post-FKT Scores of Students’ Conceptual Knowledge Responses in the Experimental and the Control Groups
Source | Type III Sum of Squares | df | Mean Square | F | Sig. |
| Pretest | 84.555 | 1 | 84.555 | 21.306 | .001 |
| Group | 256.485 | 1 | 256.485 | 64.627 | .001 |
| Error | 154.778 | 39 | 3.969 | ||
| *p < 0.05 | |||||
A summary ANOVA is presented in Tables 5 and 6. Students’ performance in seven dimensions on the post-FKT is compared for procedural knowledge and conceptual knowledge for the experimental and control groups. Results indicate a significant mean difference between the experimental and control group students’ procedural knowledge of equivalent fractions, ordering of fractions, subtraction of fractions, division of fractions, and fraction transfer. The results indicate that the students in the experimental group demonstrated better understanding than did the control group students.
Table 5
Summary of ANOVA Comparing the Mean Post-FKT Scores of Students’ Procedural Knowledge for Seven Dimensions.
Experimental Group | Control Group | |||||||
Dimension of FKT | n | M | SD | n | M | SD | MS | F |
| Fraction Concept | 21 | 1.83 | .38 | 21 | 1.66 | .48 | .183 | 1.55 |
| Equivalent Fractions | 21 | 1.87 | .44 | 21 | 1.33 | .76 | .37 | 8.25* |
| Ordering of Fractions | 21 | 2.00 | .00 | 21 | 1.61 | .60 | .16 | 9.91* |
| Addition of Fractions | 21 | 1.95 | .20 | 21 | 1.83 | .38 | .09 | 1.85 |
| Subtraction of Fractions | 21 | 1.95 | .20 | 21 | 1.55 | .61 | .19 | 9.02* |
| Multiplication of Fractions | 21 | 1.91 | .28 | 21 | 1.66 | .59 | .20 | 3.28 |
| Division of Fractions | 21 | 2.00 | .00 | 21 | 1.72 | .57 | .14 | 5.66* |
| Fraction Transfer | 21 | 1.83 | .48 | 21 | .83 | .85 | .45 | 23.07* |
| *Significant at p < .05. | ||||||||
Table 6
Summary of ANOVA Comparing the Mean Post-FKT Scores of Students’ Conceptual Knowledge on Seven Dimensions
Experimental Group | Control Group | |||||||
Dimension of FKT | n | M | SD | n | M | SD | MS | F |
| Fraction Concepts | 21 | 1.83 | .38 | 21 | 1.66 | .48 | .18 | 1.56 |
| Equivalent Fraction | 21 | 1.87 | .33 | 21 | 1.33 | .68 | .27 | 11.36* |
| Fraction Ordering | 21 | 2.00 | .00 | 21 | 1.33 | .76 | .25 | 18.29* |
| Fraction Addition | 21 | 1.87 | .44 | 21 | .66 | .76 | .37 | 41.07* |
| Fraction Subtraction | 21 | 1.83 | .48 | 21 | .55 | .78 | .39 | 42.58* |
| Fraction Multiplication | 21 | 1.20 | .88 | 21 | .27 | .46 | .54 | 16.52* |
| Fraction Division | 21 | 1.20 | .88 | 21 | .00 | .00 | .45 | 33.45* |
| Fraction Transferring | 21 | 1.83 | .48 | 21 | .83 | .85 | .45 | 23.07* |
| *Significant at p < .05. | ||||||||
Table 6 indicates a significant mean difference between the experimental and control group students’ conceptual knowledge of equivalent fractions, ordering of fractions, fraction addition, fraction subtraction, fraction multiplication, fraction division, and fraction transferring. The results indicate that students in the experimental group demonstrated better understanding compared to the control group students.
Procedural Knowledge
Mean average percentages of students in the experimental and control groups giving correct answers on the post-FKT were evaluated. The results showed that 95.87% of students in the experimental group solved the items of procedural knowledge correctly, while 82.63% of students in the control group solved the items of procedural knowledge correctly. In particular, differences between the experimental and control groups were found in the dimensions of equivalent fractions, fraction addition, fraction subtraction, fraction multiplication, and fraction division (see Table 7).
Table 7
Summary of Percentages of Students in the Experimental and the Control Groups Giving Correct Answers on the Post-FKT
Experimental Group | Control Group | |||
Dimension of FKT | PK | CK | PK | CK |
| Fraction Concepts | 91.5% | 83% | 91.5% | 83% |
| Equivalent Fraction | 95% | 66.7% | 93.5% | 66.5% |
| Fraction Ordering | 100% | 83.3% | 100% | 66.5% |
| Fraction Addition | 97.5% | 91.5% | 93.5% | 33% |
| Fraction Subtraction | 100% | 77.8% | 91.5% | 27.5% |
| Fraction Multiplication | 95.5% | 83% | 60% | 13.5% |
| Fraction Division | 100% | 88.89% | 60% | 20% |
| Fraction Transferring | 91.7% | 44.4% | 91.5% | 41.5% |
| PK: procedural knowledge; CK: conceptual knowledge; FKT: Fraction Knowledge Test | ||||
Conceptual Knowledge
Mean average percentages of the students in the experimental and the control groups selecting correct answers on post-FKT were also evaluated. The results showed that 85.43% of the students in the experimental group solved the items of conceptual knowledge correctly, while only 41.63% of the students in the control group solved the items of conceptual knowledge correctly. In particular, the most striking differences between the experimental and the control groups were found in the dimensions of fraction ordering, fraction addition, fraction subtraction, fraction multiplication, and fraction division (see Table 7). These results suggest that the students in the experimental group who were taught with WBI had a better acquisition of fraction conceptions than did those in the control group who were taught by traditional instruction.
Effect Sizes
Table 2 reports the effect sizes for procedural knowledge and conceptual knowledge. The effect sizes were .81 and 1.8 for procedural knowledge and conceptual knowledge, respectively. Thus, the outcome of the WBI is a gain on the dependent variable equivalent to a move from the mean to the 79th percentile for procedural knowledge and the 96th percentile for conceptual knowledge. The effect size of both procedural knowledge and conceptual knowledge are considered large (Cohen, 1988). This large effect size was interpreted as WBI raising achievement scores on both procedural knowledge and conceptual knowledge. Equivalently, learners in the WBI performed better than the learners in the control group.
Discussion and Recommendations
The purpose of this study was to compare the effectiveness of Web-based and traditional instruction on preservice elementary teachers’ procedural knowledge and their conceptual knowledge of fractions. The main difference between the two instructional methods was that students in the experimental group were instructed with Web-based resources related to fraction concepts, while students in the control group received the same information as the experimental group with traditional instruction. The results indicated that when the preservice teachers instructed with Web-based resources related to fraction concepts, it constituted an effective method in providing students with an opportunity to promote both their procedural and conceptual understandings. These results are consistent with previous research, which found that CAI increases learning (Chen & Liu, 2007; Kulik & Kulik, 1987; Liao, 2007; McNulty, Halama, Dauzvardis, & Espiritu, 2000; Mevarech & Rich, 1985; Wilson & Harris, 2002).
Why did the preservice teachers in the experimental group gain more from working with these interactive Internet resources? Students in the experimental group built on the concepts of fraction meaning and equivalence to learn fraction operations through the interactive Internet resources. The interactive Internet resources helped them to see the purpose of constructing same size parts when they added and subtracted fractions. The construction Web sites not only helped students do the basic fraction constructions, they also helped them explain why and how they work. In addition, the interactive Internet resources helped them use visual models to experience multiplying and dividing fractions. This finding is in agreement with Bliwise (2005), who found that Web-based tutorials were helpful for teaching introductory statistics.
Second, the interactive Web sites provided a rich environment for animated demonstration. Animated demonstration made possible by the dynamic interactive Web sites facilitates connections between a mathematical expression and the situation to which it refers. It helps students not to stick to a description in words and symbols or to a diagram in a book that cannot be examined or explored. For example, to calculate 1¾ ÷ ½, the students can easily learn in the computer program “ How many ½’s are there in 1¾ ?” This finding aligns with those of Wender and Muehlboeck (2003), where animated demonstrations helped students understand statistical concepts.
The greater success of students in the experimental group may be attributed to the following: students’ participation in WBI helped them to acquire meaningful learning in both procedural and conceptual knowledge of fractions. They utilized different representations they found in the interactive Web sites. This helped them in facilitating their understanding and also encouraged their conceptual restructuring. In addition, WBI encouraged students to use interactive and virtual representations. This helped them not only to strengthen their procedural knowledge of fractions, but also to deepen their conceptual understanding of fraction computations and to avoid some struggles and frustrations. Therefore, it is recommended that mathematics teacher education programs should take into consideration the use of technology for preparing preservice teachers to teach fractions effectively in tomorrow’s mathematics classroom.
There are multiple methods and representations for doing fraction operations. The computer program plays an important role by showing dynamic and interactive representations of fractions. Preservice teachers should be acquainted with these multiple methods and should have facility not only in calculations but also in knowing how to explain why and how they work. The positive findings in this study suggest that preservice teachers can develop their accuracy in computation and understanding of fractions by using dynamic computer programs.
According to the Principles and Standards for School Mathematics, “effective mathematics teaching requires understanding what students know and need to learn and then challenging and supporting them to learn it well” (NCTM, 2000, p. 16). Ma (1999) suggested that effective teachers must have a profound understanding of mathematics. A profound understanding of mathematics means a teacher is well equipped with content knowledge. That is, a teacher is equipped to represent mathematical ideas to students in ways that will connect their prior knowledge with the mathematics they are expected to learn.
By developing content knowledge through Internet resources, preservice teachers not only could deepen their profound understanding of mathematics but also become capable of making instructional decisions that lead to meaningful activities and real-world experiences for the students in their future classrooms. Capraro, Capraro, Parker, Kulm, and Raulerson (2005) found that a lack of mathematical content knowledge leads to ineffective mathematics instruction. Therefore, if solid mathematical content knowledge leads to effective mathematics instruction, this current study suggests that WBI can lead to the needed mathematical content knowledge for effective teaching of fraction concepts.
Investigations of the use of Internet resources to improve preservice teachers’ mathematical knowledge are only just beginning. A further study is needed to see whether WBI impacts preservice teachers’ learning outcomes in other content areas such as integers, operation of integers, and percentages. In addition, future research should compare preservice teachers’ and in-service teachers’ perceptions of teaching mathematics with interactive Internet resources. The findings would be helpful for designing mathematics teacher education programs.
However, some major limitations of the study should be noted. The first limitation of this research project was that the test consisted of only two items for each of eight constructs. Future studies could add more questions to make sure the results are accurate. The second limitation of this research project was that 42 subjects were used, and therefore, our results are not generalizable. Third, subjects from only one institution and one instrument were used in the investigation. The generalizability of the observed findings to other instruments or contexts should be established. Future studies could involve more institutions and compare the outcomes. Lastly, a limitation of this research project was that the WBI emphasized only topics on fractions. Future studies could add more topics such as measurement, geometry, and data analysis.
Author Note:
The author wishes to thank Jerry P. Becker, Miran Byun, and the three anonymous reviewers for their helpful comments on an earlier draft of this article.
Cheng-Yao Lin
Southern Illinois University Carbondale
Email: [email protected]
References
Aberson, C. L., Berger, D. E., Healy, M. R., & Romero, V. L. (2003). Evaluation of an interactive tutorial for teaching hypothesis testing concepts. Teaching of Psychology, 30, 75-78.
Ball, D. L. (1990). Prospective elementary and secondary teachers’ understanding of Division. Journal for Research in Mathematics Education, 21(2), 132-144.
Becker, J. P. & Shimada, S. (Eds.) (1997). The open-ended approach: A new proposal for teaching mathematics. Reston, VA: National Council of Teachers of Mathematics.
Behr, M. J., Khoury, H. A., Harel, G., Post, T., & Lesh, R. (1997). Conceptual units analysis of preservice elementary teachers’ strategies on a rational-number-as operator task. Journal for Research in Mathematics Education, 28(1), 48-69.
Bliwise, N.G. (2005). Web-based tutorials for teaching introductory statistics. Journal Educational Computing Research, 33(3), 309-325.
Capraro, R. M., Capraro, M. M., Parker, D., Kulm, G., & Raulerson, T. (2005). The mathematics content knowledge role in developing preservice teachers’ pedagogical content knowledge. Journal of Research in Childhood Education, 20(2), 108-124.
Carpenter, T.P., Fennema, E., Peterson, P.L., & Carey, D.A. (1988). Teachers’ pedagogical content knowledge of students’ problem solving in elementary arithmetic. Journal for Research in Mathematics Education, 19(5), 385-401.
Chang, K., Sung, Y., & Lin, S. (2006). Computer-assisted learning for mathematical problem solving. Computers and Education, 46(2), 140-151.
Chen, C.J., & Liu, P.L. (2007). Personalized computer-assisted mathematics problem-solving program and its impact on Taiwanese students. Journal of Computers in Mathematics and Science Teaching, 26(2), 105-121.
Chinnapan, M. (2000). Preservice teachers understanding and representation of fractions in a JavaBars environment. ERIC Document Reproduction Service No. EJ623921.
Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale, NJ: Lawrence Earlbaum Associates.
Cramer, K., Post, T. R., & del Mas, R. C. (2002). Initial fraction learning by fourth- and fifth-grade students: A comparison of the effects of using commercial curricula with the effects of using the Rational Number Project curriculum. Journal for Research in Mathematics Education, 33(2), 111-144.
Crook, C. (1994). Computers and the collaborative experience of learning. London: Routledge.
Darling-Hammond, L. (1999). Teacher quality and student achievement: A review of state policy evidence. Retrieved from the Center for the Study of Teaching and Policy Web site: http://depts.washington.edu/ctpmail/PDFs/LDH_1999.pdf
Davis, E. J., & Thipkong, S. (1991). Preservice elementary teachers’ misconceptions in interpreting and applying decimals. School Science and Mathematics, 91(3), 93-99.
Donovan, W., & Nakhleh, M. (2007). Student use of web-based tutorial materials and understanding of chemistry concepts. Journal of Computers in Mathematics and Science Teaching, 26(4), 291-327.
Fletcher-Flinn, C. M., & Gravatt, B. (1995). The efficacy of computer-assisted instruction (CAI): A meta-analysis. Journal of Educational Computing Research, 12, 219-241.
Flores, A. (2002). Profound understanding of division of fractions. In B. Litwiller (Ed.), Making sense of fraction, ratios, and proportions. Reston, VA: National Council of Teachers of Mathematics.
Fuchs, L.S., Fuchs, D., Hamlett, C. L., & Appleton, A. C. (2002). Explicitly teaching for transfer: Effects on the mathematical problem-solving performance of students with mathematics disabilities. Learning Disabilities: Research & Practice, 17(2), 90-106.
Fuchs, L.S., Fuchs, D., Hamlet, C.L., & Powell, S.R. (2006). The effects of computer-assisted instruction on number combination skill in at-risk first graders. Journal of Learning Disabilities, 39(5), 467-475.
Ganguli, A. (1992). The effect on students’ attitudes of the computer as a teaching aid. Educational Studies in Mathematics, 23, 611-618.
Hannafin, R. D., Burruss, J. D., & Little, C. (2001). Learning with dynamic geometry programs: Perspectives of teachers and learners. Journal of Educational Research, 94(3), 132-144.
Hashimoto, Y., & Becker, J. P. (1999). The open approach to teaching mathematics-Creating a culture of mathematics in the classroom: Japan. In L. Sheffield (Ed.), Developing mathematically promising students. Reston, VA: National Council of Teachers of Mathematics.
Hiebert, J., & Lefevre, P. (1986). Conceptual and procedural knowledge in mathematics: An introductory analysis. In J. Hiebert (Ed.), Conceptual and procedural knowledge: The case of mathematics (pp. 1-27). Hillsdale, NJ: Lawrence Erlbaum Associates.
Hill, H.C., Rowan, B., & Ball, D. L. (2005). Effects of teachers’ mathematical knowledge for teaching on student achievement. American Educational Research Journal, 42(2), 371-406.
Hill, H.C., Schilling, S.G., & Ball, D.L. (2004). Developing measures of teachers’ mathematics knowledge for teaching. The Elementary School Journal, 105(1), 11-30.
Iskander, W., & Curtis, S. (2005). Use of colour and interactive animation in learning 3D vectors. Journal of Computers in Mathematics and Science Teaching, 24(2), 149-156.
Izsak, A. (2008). Mathematical knowledge for teaching fraction multiplication. Cognition and Instruction, 26(1), 95-143.
Kulik, J. A., & Kulik, C. L. C. (1987). Review of recent research literature on computer-based instruction. Contemporary Educational Psychology, 12, 222-230.
Li, Q., & Edmonds, K. A. (2005). Mathematics and at-risk adult learners: Would technology help? Journal of Research on Technology in Education, 38(2), 143-166.
Liao, Y-K. (2007). Effects of computer-assisted instruction on students’ achievement in Taiwan: A meta-analysis. Computers & Education, 48(2), 216-233.
Lin, C. (2008). Preservice teachers’ beliefs about using technology in the mathematics classroom. Journal of Computers in Mathematics and Science Teaching, 27(3), 341-360.
Ma, L. (1999). Knowing and teaching elementary mathematics: Teachers’ understanding of fundamental mathematics in China and the United States. Mahwah, NJ: Lawrence Erlbaum.
McNeil, B. J., & Nelson, K. R. (1991). Meta-analysis of interactive video instruction: A ten year review of achievement effects. Journal of Computer-Based Instruction, 18, 1-6.
McNulty, J. A., Halama, J., Dauzvardis, M. F., & Espiritu, B. (2000). Evaluation of Web-based computer-aided instruction in basic science course. Academic Medicine, 75, 59-63.
Mevarech, A. R., & Rich, Y. (1985). Effects of computer assisted mathematics instruction on disadvantaged pupils’ cognitive and affective development. Journal of Educational Research, 79(1), 5-11.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
National Curriculum for England. (2008). Retrieved from the Qualifications and Curriculum Authority Web site: http://www.nc.uk.net/webdav/harmonise?Page/@id=6016
Niewiec, R., & Walberg, H. (1987). Comparative effects of computer-assisted instruction: A synthesis of reviews. Journal of Educational Computing Research, 3, 19-37.
Ragasa, C.Y. (2008). A comparison of computer-assisted instruction and the traditional method of teaching basic statistics. Journal of Statistics Education, 16(1). Retrieved from http://www.amstat.org/publications/jse/v16n1/ragasa.html
Rizvi, N. F. & Lawson, M. J. (2007). Prospective teachers’ knowledge: Concept of division. International Education Journal, 8(2), 377-392.
Rowan, B., Chiang, F., & Miller, R. (1997). Using research on employees’ performance to study the effects of teachers on students’ achievement. Sociology of Education, 70(4), 256-284.
Schorr, R. Y., & Goldin, G. A. (2008). Students’ expression of affect in an inner-city SimCalc classroom. Educational Studies in Mathematics, 68(2), 131-148.
Selden, A., & Selden, J. (1997). Preservice teachers conceptions of mathematics and how to teach it. Retrieved from the Mathematical Association of America Web site: http://www.maa.org/t_and_l/sampler/rs_3.html
Simon, M.A. (1993). Prospective elementary teachers’ knowledge of division. Journal for Research in Mathematics Education, 24(3), 233-254.
Skemp, R. (1987). The psychology of learning mathematics. Hillsdale, NJ: Erlbaum.
Staub, F., & Stern, E. (2002). The nature of teachers’ pedagogical content beliefs matters for students’ achievement gains: Quasi-experimental evidence from elementary mathematics. Journal of Educational Psychology, 94(2), 344-355.
Tilidetzke, R. (1992). A comparison of CAI and traditional instruction in a college algebra course. Journal of Computers in Mathematics and Science Teaching, 11, 53-62.
Tirosh, D. (2000). Enhancing prospective teachers’ knowledge of children’s conceptions: The case of division of fractions. Journal for Research in Mathematics Education, 31(1), 5-25.
Wender, K. F., & Muehlboeck, J. S. (2003). Animated diagrams in teaching statistics. Behavior Research Methods, Instruments, & Computers, 35, 255-258.
Wilson, S.P., & Harris, A. (2002). Evaluation of the psychology place: A Web-based instructional tool for psychology courses. Teaching of Psychology, 29, 165-168.
![]()