In 1986 Lee Shulman launched a new way of thinking about the knowledge teachers need for teaching with a construct that he called pedagogical content knowledge (PCK). This new way of thinking about the knowledge teachers need for teaching called for the integration of content knowledge (the knowledge previously considered the primary knowledge for teachers) and pedagogical knowledge (the knowledge about teaching and learning). The intersection of these two knowledge bases, PCK, was described as the way of representing and formulating subject matter knowledge, the knowledge that makes the subject matter comprehensible to learners (Shulman, 1986, 1987; Wilson, Shulman, & Richert, 1987). More specifically, Shulman (1986) characterized a teacher’s PCK as knowledge of
the most regularly taught topics in one’s subject area, the most useful forms of representation of those ideas, the most powerful analogies, illustrations, examples, explanations, and demonstrations … including an understanding of what makes the learning of specific concepts easy or difficult: the concepts and preconceptions that students of different ages and backgrounds bring with them to the learning. ( p. 9)
During those early discussions of the construction of knowledge growth in teaching, teacher preparation programs were challenged to determine how they might guide the development of this teacher knowledge. Some programs honed in on the development of six primary domains of knowledge essential for effective instruction: subject matter knowledge, pedagogical knowledge, knowledge of schools, knowledge of learners, and curricular knowledge, with PCK as the essence of the intersection of these five domains of knowledge (Niess, 2001). The relationship was viewed as a complex and integrated structure where no domain was totally distinct or separate from the other, with the relative amount of overlap and interaction among the domains constantly changing as preservice teachers made sense of and prioritized the multiple factors affecting student learning.
Attention to PCK through research studies provided insight into the preparation of preservice mathematics teachers’ development of PCK (Ball, 1988; Civil, 1992; Grossman, 1991; McDiarmid, 1990; Simon & Brobeck, 1993; Simon & Mazza, 1993; Wilcox et al., 1990). Grossman’s (1989, 1990) research identified four central components of PCK to focus the description and understanding of the knowledge needing development in the preparation programs: (a) an overarching conception of what it means to teach a particular subject; (b) knowledge of instructional strategies and representations for teaching particular subject matter topics; (c) knowledge of students’ understandings, thinking, and learning in the subject area; (d) knowledge of curriculum and curriculum materials with learning subject matter (Borko & Purtnam, 1996).
As this understanding of PCK evolved, modern digital technologies also began to be recognized as useful for teaching and learning. During the late 1970s and 1980s, the focus in mathematics education was on identifying places in mathematics instruction for inserting digital technology applications. A myriad of software programs afforded drill and practice in a variety of environments that were more entertaining than traditional paper-and-pencil worksheets for providing practice with computational skills. Graphing calculators offered capabilities for efficiently generating visuals of graphs useful for demonstrating mathematical ideas such as slope and y-intercept for linear functions and points of intersection for multiple functions.
The primary vision for employing mathematical digital technologies was for demonstration and verification of ideas previously developed in the classroom. Calculators – from limited four-function calculators to scientific calculators – were restricted with the belief that these tools trivialized the mathematics rather than engaging students in learning mathematics. The lack of an in-depth integration of these technologies prompted Kaput’s (1992) lament that the “major limitations of computer use in the coming decades are likely to be less a result of technological limitations than a result of limited human imagination and the constraints of old habits and social structures” (p. 515).
An examination of mathematics teachers’ PCK in the late 1980s and early 1990s revealed an overarching conception that teachers’ beliefs about how to teach mathematics generally were aligned with how they learned mathematics. Although a few teachers embraced the use of graphing calculators, spreadsheets, and software like Logo and Geometric Supposer, many did not. Mathematics teachers’ knowledge of instructional strategies and representations for teaching particular mathematical topics relegated the application of such digital technologies to demonstration, verification, and drill and practice. Their knowledge of students’ understandings, thinking, and learning in mathematics held to the importance of mastery of skills with paper and pencil prior to using modern digital technologies (Kastberg & Leatham, 2005; Walen, Williams, & Garner, 2003; Yoder, 2000).
Furthermore, access to technology without necessary knowledge of related curriculum materials did not encourage teachers to incorporate the technology in their classroom instruction (Kastberg & Leatham, 2005). “In the absence of professional development on instructional technology and curriculum materials that integrate technology use into the lesson content, teachers are not particularly likely to embed technology-based or technology-rich activities into their courses” (Ferrini-Mundy & Breaux, 2008, p. 437-438).
Fast forward to 2008 to see that many mathematics teachers’ PCK lacks a solid and consistent integration of modern digital technologies in mathematics curriculum and instruction. Technologies, such as dynamic geometry tools or advanced graphing calculators with computer algebra systems (CAS), are primarily used for modeling and providing examples, where students imitate the actions and use the technologies for verification, demonstration, and drill and practice. In essence then, while digital technologies have evolved, strategies for their effective integration into the learning of mathematics have not evolved as rapidly.
Mathematics TPACK: The Total Package for Teaching Mathematics
As time shifted and digital technologies became more accessible and incorporated into citizens’ work and play, the International Society for Technology and Education (ISTE) challenged teachers to think about the technology skills and knowledge students would need in an increasingly technology savvy society. By the turn of the 21st century, the National Education Technology Standards for Students (NETS-S; ISTE, 2000) were released with the goal of supporting the evolution of effective use of appropriate technologies in school settings.
ISTE recognized that these new standards called for different teacher knowledge than was currently operating in the schools. Within the following 2 years, the National Educational Technology Standards for Teachers (NETS-T; ISTE, 2002) were also released. Although embedded in a rapidly changing digital society, little real instructional change filtered into classrooms. Therefore, ISTE moved to shift the focus of the NETS-S from basic skills and knowledge needed to operate the technology to learning how to effectively use the technology; the NETS-S were updated in 2007. Subsequently, to assist teachers in responding to the call of learning environments supported by multiple technologies, a revision of the teacher standards was released in 2008.
These standards effectively shifted the focus on digital technologies toward a concern about the curriculum and instructional uses of the digital tools and resources. Earle (2002) framed this shift most clearly:
Integrating technology is not about technology – it is primarily about content and effective instructional practices. Technology involves the tools with which we deliver content and implement practices in better ways. Its focus must be on curriculum and learning. Integration is defined not by the amount or type of technology used, but by how and why it is used. (p. 8)
Numerous researchers focused on the integration of technology, content, and pedagogy in much the same way that Shulman described PCK, to gain a broader perspective on the knowledge teachers need for teaching with technology. In essence, they defined technological pedagogical content knowledge (TPCK) as that body of knowledge teachers needed for teaching with and about technology in their assigned subject areas and grade levels. TPCK was presented as the interconnection and intersection of content, pedagogy (teaching and student learning), and technology (Margerum-Leys & Marx, 2002; Mishra & Koehler, 2006; Niess, 2005; Pierson, 2001). The idea of TPCK developed to the point that the American Association of Colleges of Teacher Education supported the collaboration of multiple TPCK authors in the development of The Handbook of Technological Pedagogical Content Knowledge for Educators (AACTE Committee on Technology and Innovation, 2008).
TPCK was proposed as the strict intersection between the three individual knowledge constructs of technology, pedagogy, and subject matter content. The discussion often expanded beyond this intersection to include the overlapping constructs of technological content knowledge (TCK), technological pedagogical knowledge (TPK), and PCK (Koehler & Mishra, 2008). With the importance of the interplay between these constructs, TPCK has, over time, been recast as TPACK, or the total package required for integrating technology, pedagogy, and content knowledge in the design of instruction for thinking and learning mathematics with digital technologies (Niess, 2008; Thompson & Mishra, 2007). As technology, students, teachers, and classroom contexts change, TPACK provides a dynamic framework for viewing teachers’ knowledge necessary for the design of curriculum and instruction focused on the preparation of their students for thinking and learning mathematics with digital technologies.
Mathematics Teacher TPACK Standards
The National Council of Teachers of Mathematics (NCTM) supported this new vision of TPACK early in 2000 with its Technology Principle in its standards for a new century, stating that “Technology is essential in teaching and learning mathematics; it influences the mathematics that is taught and enhances students’ learning” (NCTM, 2000, p. 24). NCTM recognized and advocated the importance of the types of experiences teachers needed to be prepared to meet this standard. “If teachers are to learn how to create a positive environment that promotes collaborative problem solving, incorporates technology in a meaningful way, invites intellectual exploration, and supports student thinking, they themselves must experience learning in such an environment” (NCTM, 2007, p. 119). Similarly, the Association for Mathematics Teacher Educators (AMTE) advocated for enhancing the preparation of mathematics teachers in their Technology Position Statement: “Mathematics teacher preparation programs must ensure that all mathematics teachers and teacher candidates have opportunities to acquire the knowledge and experiences needed to incorporate technology in the context of teaching and learning mathematics” (AMTE, 2006). Yet, the question remained: What do these recommendations mean for improving the preparation of mathematics teachers?
The AMTE Technology Committee, whose role is to promote the investigation, engagement, and evaluation of uses of technology in mathematics teacher education and to recommend policy related to technology issues pertaining to enhancing mathematics teacher education programs, began addressing this question, initiating work on a set of mathematics-specific standards for TPACK. Given their charge, the AMTE Technology Committee considered the identification of directions and standards for mathematics teaching essential for promoting the improvement of mathematics education in the 21st century.
Beginning in 2007, the Committee focused on the task of creating a set of mathematics teacher standards to promote the implementation of technology in the context of teaching and learning mathematics in grades preK-12 as envisioned in the NETS-T. Although the NETS-T and NETS-S have been revisited and updated, neither set of standards provides content-specific ideas that address what students or teachers should know about using technology for learning mathematics. Therefore, these new mathematics teacher standards are intended to provide a framework for guiding professional practice that supports the improvement of mathematics teaching and learning. The themes in the standards are framed around the TPACK ideas that Niess (2005) adapted from Grossman’s four components of PCK. The themes consider the teacher knowledge of incorporating technology in teaching mathematics as the knowledge and beliefs teachers demonstrate consistent with
- An overarching conception about the purposes for incorporating technology in teaching mathematics;
- Knowledge of students’ understandings, thinking, and learning of mathematics with technology;
- Knowledge of curriculum and curricular materials that integrate technology in learning and teaching mathematics;
- Knowledge of instructional strategies and representations for teaching and learning mathematics with technologies.
A draft of the standards was presented to a working group session at the 12th annual conference of the AMTE in January 2008. Changes were made to the standards reflecting suggestions from the working group session. The updated standards draft was then presented at the 19th annual Society for Information Technology and Teacher Education (SITE) conference. As a followup, the standards were then disseminated to the AMTE Technology Committee, AMTE working group session participants, and SITE panel participants with a request for feedback. Subcommittees of the AMTE Technology Committee were then assigned to revisit other standards documents, such as the new versions of the NETS-S and NETS-T and to further revise the standards draft. Appendix A provides the current proposed draft of mathematics teacher TPACK standards and indicators.
Development of Mathematics Teachers’ TPACK
In reviewing the draft version of the Mathematics Teacher TPACK Standards and Indicators, one of the authors interviewed a former undergraduate mathematics education major (called Mary for this discussion). Mary was a student in an undergraduate setting where technology was used in the teaching and learning of mathematics. Specifically, graphing calculators were used in her discrete mathematics course, and Geometer’s Sketchpad was used extensively in her modern geometry course. After graduation, Mary taught Algebra I in a large suburban high school and was interviewed at the end of her third year in the classroom. She identified that Geometer’s Sketchpad continued to be an important technological tool for her teaching and learning and that it had helped her learn non-Euclidean geometries. Geometer’s Sketchpad was available at her school and was used by another teacher in her school. However, Mary chose not to use this software with her Algebra I students and thought that the software was only appropriate for use in a geometry class.
Mary reported that she primarily used graphing calculators for computation but not exploration. In her first 3 years of teaching, Mary indicated using technology only one time to teach a mathematical concept. The lesson she described had the students graph systems of linear equations and discover if and where the lines intersected, an appropriate use of the graphing calculator. Mary’s lesson provided evidence of some of the indicators in the TPACK Standards I and II. Specifically, Mary planned a student-centered, technology-based lesson that promoted higher order thinking in her students, but this activity was a one-time occurrence in a 3-year time span.
Mary’s case suggests different levels of the integrated knowledge of TPACK. Although the Mathematics Teacher TPACK Standards and Indicators set goals for technology integration, the standards themselves do not provide information on how teachers such as Mary progressively gain this integrated knowledge for appropriately teaching mathematics with suitable technologies. This recognition raises important questions. How does TPACK develop? Is there a process in which teachers gain mathematics TPACK knowledge? Do teachers suddenly display this knowledge in their professional practice? What is needed is a model that captures the progression of mathematics TPACK as teachers integrate technology into the teaching and learning of mathematics.
Niess, Sadri, and Lee (2007) proposed a developmental model for TPACK emanating from Everett Rogers’ (1995) model of the innovation-decision process (first introduced in 1962 concerning societal diffusion of innovations). Rogers described a five-stage, sequential process by which a person makes a decision to adopt or reject a new innovation. Niess et al. reframed this process in terms of mathematics teachers learning to integrate a technology that they had not yet integrated in teaching and learning mathematics. Over a 4-year period, they observed many teachers learning about spreadsheets and how to integrate spreadsheets as learning tools in their mathematics classrooms. Analysis of these observations found that teachers progressed through this five-stage developmental process when learning to integrate a particular technology in teaching and learning mathematics:
- Recognizing (knowledge), where teachers are able to use the technology and recognize the alignment of the technology with mathematics content yet do not integrate the technology in teaching and learning of mathematics.
- Accepting (persuasion), where teachers form a favorable or unfavorable attitude toward teaching and learning mathematics with an appropriate technology.
- Adapting (decision), where teachers engage in activities that lead to a choice to adopt or reject teaching and learning mathematics with an appropriate technology.
- Exploring (implementation), where teachers actively integrate teaching and learning of mathematics with an appropriate technology.
- Advancing (confirmation), where teachers evaluate the results of the decision to integrate teaching and learning mathematics with an appropriate technology.
Considering these five levels for integrating technology in teaching and learning mathematics relying on the integration of knowledge of technology, pedagogy, and content (TPACK), AMTE’s Technology Committee created a visual description for thinking about the TPACK levels. Figure 1 depicts levels in which teachers engage as they develop their knowledge and understandings in ways that merge multiple knowledge bases ― technology, content, and pedagogy. On the left side of the graphic, the figure highlights PCK as the intersection of pedagogy and content. Then, as knowledge of technology expands and begins to intersect with pedagogical and content knowledge, the teacher knowledge base that emerges is the knowledge described as TPACK – where teachers actively engage in guiding student learning of mathematics with appropriate technologies.
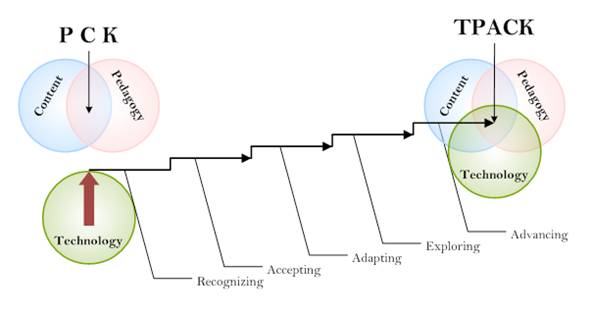 Figure 1. Visual description of teacher levels as their thinking and understanding merge toward the interconnected and integrated manner identified by TPACK.
Figure 1. Visual description of teacher levels as their thinking and understanding merge toward the interconnected and integrated manner identified by TPACK.
An important caveat when thinking about these levels and the progression toward TPACK is that, while appearing linear with respect to a particular technology, the transition from one level to another does not display a regular, consistently increasing pattern. As with Rogers’ innovation-decision process, the emergence of a new technology requires rethinking its acceptance for teaching and learning mathematics. It requires rethinking the content and the pedagogies, as well. Thus, the levels are proposed to display more of an iterative process in the development of TPACK. Some aspects of what is learned about teaching a particular topic with one technology may provide a disposition toward acceptance of another technology, but teachers often challenge an integration that is different from the way they learned specific mathematics concepts.
A Mathematics Teacher TPACK Development Model
While the Mathematics Teacher TPACK Standards provide a lens for considering the actions of teachers who have an integrated knowledge of technology, content, and pedagogy, the recognition of the levels of thinking and understanding as they begin to develop this TPACK calls for clarification. Mishra and Koehler (2006) dissected the basic TPACK framework into its knowledge components beginning with content knowledge (CK), pedagogical knowledge (PK), and pedagogical content knowledge (PCK). As technology knowledge (TK) becomes integrated with these components, additional components emerge: technological content knowledge (TCK) and technological pedagogical knowledge (TPK) are added to PCK as intersections of the content, pedagogical, and technological knowledge. They discussed TCK as follows: “teachers need to know not just the subject matter they teach but also the manner in which the subject matter can be changed by the application of technology” (p. 1028). TPK was described as “knowledge of the existence, components, and capabilities of various technologies as they are used in teaching and learning settings, and conversely, knowing how teaching might change as the result of using particular technologies” (p. 1028).
These added descriptions explain the various intersections in general terms; however, they are not embedded within the context of developing mathematics TPACK. The AMTE Technology Committee decided to unpack the teacher levels in thinking and understanding in the process of the development of TPACK, as described in the Mathematics Teacher TPACK Standards. Four major themes further framed the Mathematics Teacher TPACK Development Model: Curriculum and Assessment, Learning, Teaching, and Access. Rather than treating Curriculum and Assessment separately, the Technology Committee decided that these themes should be grouped to highlight the connection between the curricular and assessment decision-making process. From this thinking, the Technology Committee developed descriptors as outlined in Table 1.
Table 1
Descriptors for Major Themes in the Mathematics Teacher TPACK Development Model
Theme | Descriptors |
Curriculum and Assessment |
|
Learning |
|
Teaching |
|
Access |
|
The next step was to expand the descriptors through the TPACK levels and identify specific examples for each descriptor at each of the TPACK levels using detailed descriptions of the levels provided from Niess’ (2007) work. Appendix B expands the Mathematics Teacher TPACK Development Model, providing detailed (albeit not exhaustive) actions that teachers may experience and engage in while adapting technology in their teaching in order to enhance student learning.
As an example of how the Curriculum and Assessment theme engages the shift in mathematics subject matter, consider teachers who initially recognize that technology can be used to support mathematical processes such as square root. Teachers’ thought processes progress toward an acceptance of the technology as they incorporate it as an alternative for the algorithmic procedure for finding a square root, although they remain concerned about the loss of algorithmic skills for finding square roots.
At the adapting level teachers are willing to try some activities in the classroom that typically mimic activities from their own professional development experiences. Perhaps they focus on estimating square roots and then compare their estimates with calculator results. At some point, these teachers begin to explore their specific mathematics curriculum in search of places to incorporate the calculator square root function as a tool for shifting the subject matter emphasis toward an application of the concept of square roots, where students are allowed to find the results using appropriate technologies such as calculators for identifying the square root results.
Teachers at the advancing level not only incorporate calculators for working on other mathematical topics, they actually challenge the curriculum, looking for how that curriculum might shift as a result of the calculator’s capability for finding square roots. These teachers are more willing to make changes in their curriculum, adding and dropping particular topics as a result of the technological capabilities. Now, these teachers no longer focus on teaching the square root algorithm and allow students to use calculators to identify actual square roots, if such a result is needed. With these teacher decisions, the curriculum is shifted toward teaching the concept of square root and estimating square roots, rather than the more procedural emphasis on finding square roots; in fact, a new curriculum component may be introduced to focus on understanding the difference between approximate and exact solutions.
From the Learning theme, teachers might recognize that technology provides an instructional tool for their mathematics classes but at the same time they might perceive that the technology potentially interferes with learning key mathematical ideas. Therefore, the technology is allowed only outside of the regular instructional activities. At the accepting level, teachers see that the technology is here to stay and form their own attitudes and beliefs regarding its use in their instruction. At this level teachers might have concerns that students do not develop appropriate mathematical thinking skills; so technology is used to check their work, first completed with paper and pencil. At the adapting level, teachers start experimenting with the technology to determine whether to adopt or reject it. They might consider it to be useful but still express questions about students developing appropriate mathematical thinking skills. Therefore, although students use technology for most topics, testing remains mostly technology free.
At the exploring level, teachers who decide to adopt the technology in their classrooms start integrating teaching and learning of mathematics with appropriate technologies; they plan, implement, and reflect on teaching and learning with a possible concern for guiding students in understanding mathematics using the technology as a tool for learning. At the last level, advancing, teachers are likely to evaluate the results of the decision to integrate technology in teaching and learning mathematics. As a result, technology integration becomes integral (rather than in addition) to the development of the mathematics students are learning.
TPACK Next Steps
This description of the overarching construct of TPACK provides specific and identifiable constructs of teacher knowledge associated with TPACK, accompanied with a model or a framework that supplies context for the constructs. The themes, levels, and descriptors provide structured detail to permit various groups to use the model independently. The five levels (recognizing, accepting, adapting, exploring, and advancing) expand upon the themes of Curriculum and Assessment, Learning, Teaching, and Access. The descriptors for each level and the mathematics examples provide further delineation of the themes and levels. This structure may be useful for teachers, researchers, teacher educators, professional development consultants, and school administrators to guide development and evaluation of professional development activities, mathematics education programs, and school mathematics programs.
Teachers may find the model useful in assessing their level of mathematics TPACK using the descriptors and examples, and then plan their individual professional development in mathematics instructional technology. Principals and professional development consultants, with specific work guided by TPACK, are able to plan more informed and directed professional development for groups of teachers, as well as evaluate the effectiveness of their programs. Teacher educators might find the TPACK levels helpful in evaluating and planning the technology preparation of their preservice and in-service students. The Mathematics Teacher TPACK Developmental Model establishes common constructs and language that should help researchers connect their work to that of others and within a larger context.
A number of questions remain about the model. For example, a mathematics teacher may be at different levels for different themes and descriptors (Appendix B). That is, in the Curriculum and Assessment theme, one might be at the exploring level by demonstrating a willingness to develop personal ideas for using technologies in instruction, yet at the recognizing level when it comes to allowing students to use technologies during assessments. This proposal must be tested. Moreover, moving from one level to another may require different sets of experiences for different levels and for different teachers. What are these sets of experiences? Do experiences exist that cause teachers to regress from one level to a previous one? Do teachers skip levels?
This model generates a number of new questions for mathematics educators; however, these questions are much more focused and specific than what typically emerge without such a model. Moreover, the answers to these questions, should they be answered, will have a ready-made framework for a mathematics context. In this way, mathematics education moves forward in the understanding of the impact of technology on the learning of mathematics.
The Mathematics Teacher TPACK Standards and the corresponding TPACK Development Model are works in progress that may change as new technologies are introduced into mathematics classrooms and as more research is conducted in classrooms that carefully examine and describe the teaching and learning. A directed focus on understanding mathematics teachers’ TPACK will continue to push the uses of technology in the mathematics classroom, as well as outside of our current limited human imagination.
References
AACTE Committee on Innovation and Technology (Eds). (2008). Handbook of technological pedagogical content knowledge (TPCK) for educators. New York: Routledge
Association of Mathematics Teacher Educators. (2006). Preparing teachers to use technology to enhance the learning of mathematics. Retrieved from http://www.amte.net/
Ball, D. L. (1988). Knowledge and reasoning in mathematical pedagogy: Examining what prospective teachers bring to teacher education. Unpublished doctoral dissertation, Michigan State University, East Lansing.
Borko, H., & Putnam, T. (1996). Learning to teach. In D. C. Berliner & R. C. Calfee (Eds.), Handbook of educational psychology (pp. 673-708), New York: Simon & Schuster Macmillan.
Civil, M. (1992, April). Prospective elementary teachers’ thinking about mathematics. Paper presented at the annual meeting of the American Educational Research Association, San Francisco, CA.
Earle, R.S. (2002). The integration of instructional technology into public education: Promises and challenges. ET Magazine, 42(1), 5-13.
Ferrini-Mundy, J., & Breaux, G. A. (2008). Perspectives on research, policy, and the use of technology in mathematics teaching and learning in the United States. In G. W. Blume & M. K. Heid (Eds.), Research on technology and the teaching and learning of mathematics: Volume 2. Cases and perspectives (pp. 427-448). Charlotte, NC: Information Age Publishing.
Grossman, P. L. (1989). A study in contrast: Sources of pedagogical content knowledge for secondary English. Journal of Teacher Education, 40(5), 24-31.
Grossman, P. L. (1990). The making of a teacher: Teacher knowledge and teacher education. New York: Teachers College Press.
Grossman, P. L. (1991). Overcoming the apprenticeship of observation in teacher education coursework. Teaching and Teacher Education, 7, 245-257.
International Society for Technology in Education. (2000). National educational technology standards for students: Connecting curriculum and technology. Eugene, OR: International Society for Technology in Education.
International Society for Technology in Education. (2002). National educational technology standards for teachers: Preparing teachers to use technology. Eugene, OR: International Society for Technology in Education.
International Society for Technology in Education. (2007). National educational technology standards and performance indicators for students. Eugene, OR: International Society for Technology in Education.
International Society for Technology in Education. (2008). National educational technology standards and performance indicators for teachers. Eugene, OR: International Society for Technology in Education.
Kaput, J. (1992). Technology and mathematics education. In. D. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 515-556). New York: MacMillan Publishing.
Kastberg, S., & Leatham, K. (2005). Research on graphing calculators at the secondary level: Implications for mathematics teacher education. Contemporary Issues in Technology and Teacher Education, 5(1). Retrieved from https://citejournal.org/vol5/iss1/mathematics/article1.cfm
Koehler, M. J. & Mishra, P. (2008). Introducing technological pedagogical content knowledge. In AACTE Committee on Innovation and Technology (Eds)., Handbook of technological pedagogical content knowledge (TPCK) for educators (pp. 3-29). New York: Routledge.
Margerum-Leys, J., & Marx, R. W. (2002). Teacher knowledge of educational technology: A study of student teacher/mentor teacher pairs. Journal of Educational Computing Research, 26(4), 427-462.
McDiarmid, G. W. (1990). Challenging prospective teachers’ beliefs during early field experience: A quixotic undertaking? Journal of Teacher Education, 41(3), 12-20.
Mishra, P., & Koehler, M. J. (2006). Technological pedagogical content knowledge: A framework for teacher knowledge. Teachers College Record, 108(6), 1017-1054.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (2007). Mathematics teaching today: Improving practice, improving student learning (2nd ed.). Reston, VA: Author.
Niess, M. L. (2001). Research into practice: A model for integrating technology in preservice science and mathematics content-specific teacher preparation. School Science and Mathematics, 101(2), 102-109.
Niess, M. L. (2005). Preparing teachers to teach science and mathematics with technology: Developing a technology pedagogical content knowledge. Teaching and Teacher Education, 21, 509-523.
Niess, M. L. (2007, June). Mathematics teachers developing technological pedagogical content knowledge (TPCK). Paper presented at IMICT2007, Boston, MA.
Niess, M. L. (2008). Knowledge needed for teaching with technologies – Call it TPACK. AMTE Connections, 17(2), 9-10.
Niess, M. L., Sadri, P., & Lee, K. (2007, April). Dynamic spreadsheets as learning technology tools: Developing teachers’ technology pedagogical content knowledge (TPCK). Paper presented at the meeting of the American Educational Research Association Annual Conference, Chicago, IL.
Pierson, M. E. (2001). Technology integration practices as a function of pedagogical expertise. Journal of Research on Computing in Education, 33(4), 413-429.
Rogers, E. M. (1995). Diffusion of innovations. New York, Free Press.
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15, 4-14.
Shulman, L. S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57, 1-22.
Simon, M. A., & Brobeck, S. (1993, March). Changing views of mathematics learning: A case study of a prospective elementary teacher. Paper presented at the annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (PME-NW), Monterey, CA.
Simon, M. A., & Mazza, W. (1993, October). From learning mathematics to teaching mathematics: A case study of a prospective teacher in a reform-oriented program. Paper presented at the annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (PME-NA), Monterey, CA.
Thompson, A. D., & Mishra, P. (2007). Breaking news: TPCK becomes TPACK! Journal of Computing in Teacher Education, 24(2), 38, 64.
Walen, S. B., Williams, S. R., & Garner, B. E. (2003). Pre-service teachers learning mathematics using calculators: A failure to connect current and future practice. Teaching and Teacher Education, 19, 445-462.
Wilcox, S., Schram, P., Lappan, G., & Lanier, P., et al. (1990, April). The role of a learning community in changing preservice teachers’ knowledge and beliefs about mathematics education. Paper presented at the annual meeting of the American Educational Research Association, Boston, MA.
Wilson, S. M., Shulman, L. S., & Richert, A. E. (1987). ‘150 different ways’ of knowing: Representation of knowledge in teaching. In J. Calderhead (Ed.), Exploring teachers’ thinking (pp. 104-124). London: Cassell.
Yoder, A. J. (2000, October). The relationship between graphing calculator use and teachers’ beliefs about learning algebra. Paper presented at the annual meeting of the Mid-Western Educational Research Association, Chicago, IL.
Author Note:
Margaret L. Niess
Oregon State University
[email protected]
Robert N. Ronau
University of Louisville
[email protected]
Kathryn G. Shafer
Ball State University
[email protected]
Shannon O. Driskell
University of Dayton
[email protected]
Suzanne R. Harper
Miami University
[email protected]
Christopher Johnston
George Mason University
[email protected]
Christine Browning
Western Michigan University
[email protected]
S. Asli Özgün-Koca
Wayne State University
[email protected]
Gladis Kersaint
University of South Florida
[email protected]
![]()