I. Introduction
The phrase “technology and education” usually means inventing new gadgets to teach the same old stuff in a thinly disguised version of the same old way. Moreover, if the gadgets are computers, the same old teaching becomes incredibly more expensive and biased towards its dullest parts, namely the kind of rote learning in which measurable results can be obtained by treating the children like pigeons in a Skinner box.
The purpose of this essay is to present a grander vision of an educational system in which technology is used not in the form of machines for processing children but as something the child himself will earn to manipulate, to extend, to apply to projects, thereby gaining a greater and more articulate mastery of the world, a sense of the power of applied knowledge and a self-confidently realistic image of himself as an intellectual agent. Stated more simply, I believe with Dewey, Montessori, and Piaget that children learn by doing and by thinking about what they do. And so the fundamental ingredients of educational innovation must be better things to do and better ways to think about oneself doing these things.
I claim that computation is by far the richest known source of these ingredients. We can give children unprecedented power to invent and carry out exciting projects by providing them with access to computers, with a suitably clear and intelligible programming language and with peripheral devices capable of producing on-line real-time action.
Examples are: spectacular displays on a color scope, battles between computer controlled turtles, conversational programs, game-playing heuristic programs, etc. Programmers can extend the list indefinitely. Others can get the flavor of the excitement of these ideas from movies I shall show at the IFIPS meeting.
Thus in its embodiment as the physical computer, computation opens a vast universe of things to do. But the real magic comes when this is combined with the conceptual power of theoretical ideas associated with computation.
Computation has had a profound impact by concretizing and elucidating many previously subtle concepts in psychology, linguistics, biology, and the foundations of logic and mathematics. I shall try to show how this elucidation can be projected back to the initial teaching of these concepts. By doing so, much of what has been most perplexing to children is turned to transparent simplicity; much of what seemed most abstract and distant from the real world turns into concrete instruments familiarly employed to achieve personal goals.
Mathematics is the most extreme example. Most children never see the point of the formal use of language. They certainly never had the experience of making their own formalism adapted to a particular task. Yet anyone who works with a computer does this all the time. We find that terminology and concepts properly designed to articulate this process are avidly seized by the children who really want to make the computer do things. And soon the children have become highly sophisticated and articulate in the art of setting up models and developing formal systems.
The most important (and surely controversial) component of this impact is on the child’s ability to articulate the working of his own mind and particularly the interaction between himself and reality in the course of learning and thinking. This is the central theme of this paper, and I shall step back at this point to place it in the perspective of some general ideas about education. We shall return later to the use of computers.
2. The Don’t-Think-About-Thinking Paradox
It is usually considered good practice to give people instruction in their occupational activities. Now, the occupational activities of children are learning, thinking, playing and the like. Yet, we tell them nothing about those things. Instead, we tell them about numbers, grammar, and the French revolution; somehow hoping that from this disorder the really important things will emerge all by themselves. And they sometimes do. But the alienation-dropout-drug complex is certainly not less frequent.
In this respect it is not a relevant innovation to teach children also about sets and linguistic productions and Eskimos. The paradox remains: why don’t we teach them to think, to learn, to play? The excuses people give are as paradoxical as the fact itself. Basically there are two. Some people say: we know very little about cognitive psychology; we surely do not want to teach such half-baked theories in our schools! And some people say: making the children self-conscious about learning will surely impede their learning. Asked for evidence they usually tell stories like the one about a millipede who was asked which foot he moved first when he walked. Apparently the attempt to verbalize the previously unconscious action prevented the poor beast from ever walking again.
The paradox is not in the flimsiness of the evidence for these excuses. There is nothing remarkable in that: all established doctrine about education has similarly folksy foundations. The deep paradox resides in the curious assumption that our choice is this: either teach the children half-baked cognitive theory or leave them in their original state of cognitive innocence. Nonsense. The child does not wait with a virginally empty mind until we are ready to stuff it with a statistically validated curriculum. He is constantly engaged in inventing theories about everything, including himself, schools and teachers. So the real choice is: either give the child the best ideas we can muster about cognitive processes or leave him at the mercy of the theories he invents or picks up in the gutter. The question is: who can do better, the child or us’? Let’s begin by looking more closely at how well the child does.
3. The Pop-Ed Culture
One reads in Piaget’s books about children re-inventing a kind of’ Democritean atomic theory to reconcile the disappearance of the dissolving sugar with their belief in the conservation of matter. They believe that vision is made possible by streams of particles sent out like machine gun bullets from the eyes and even, at a younger age, that the trees make the wind by flapping their branches. It is criminal to react (as some do) to Piaget’s findings by proposing to teach the children “the truth.” For they surely gain more in their intellectual growth by the act of inventing a theory than they can possibly lose by believing, for a while, whatever theory they invent. Since they are not in the business of making the weather, there is no reason for concern about their meteorological unorthodoxy. But they are in the business of making minds—notably their own—and we should consequently pay attention to their opinions about how minds work and grow.
There exists amongst children, and in the culture at large, a set of popular ideas about education and the mind. These seem to be sufficiently widespread, uniform and dangerous to deserve a name, and I propose “The PopEd Culture.” The following examples of Pop-Ed are taken from real children. My samples are too small for me to guess at their prevalence. But I am sure very similar trends must exist very widely and that identifying and finding methods to neutralize the effects of Pop-Ed culture will become one of the central themes of research on education.
EXAMPLES OF POP-ED THINKING
(a) Blank-Mind Theories. Asked how one sets about thinking a child said: “Make your mind a blank and wait for an idea to come.” This is related to the common prescription for memorizing: “Keep your mind a blank and say it over and over.” There is a high correlation, in my small sample, between expressing something of this sort and complaining of inability to remember poetry!
(b) Getting-It Theories. Many children who have trouble understanding mathematics also have a hopelessly deficient model of what mathematical understanding is like. Particularly bad are models which expect understanding to come in a flash, all at once, ready made. This binary model is expressed by the fact that the child will admit the existence of only two states of knowledge often expressed by “I get it” and “I don’t get it.” They lack—and even resist—a model of understanding something through a process of additions, refinements, debugging and so on. These children’s way of thinking about learning is clearly disastrously antithetical to learning any concept that cannot be acquired in one bite.
(c) Faculty Theories. Most children seem to have, and extensively use, an elaborate classification of mental abilities: “He’s a brain”, “He’s a retard,” “He’s dumb,” “I’m not mathematical-minded.” The disastrous consequence is the habit of reacting to failure by classifying the problem as too hard, or oneself as not having the required aptitude, rather than by diagnosing the specific deficiency of knowledge or skill.
4. Computer Science as a Grade School Subject
Talking to children about all these bad theories is almost certainly inadequate as an effective antidote. In common with all the greatest thinkers in the philosophy of education I believe that the child’s intellectual growth must be rooted in his experience. So I propose creating an environment in which the child will become highly involved in experiences of a kind to provide rich soil for the growth of intuitions and concepts for dealing with thinking, learning, playing, and so on. An example of such an experience is writing simple heuristic programs that play games of strategy or try to outguess a child playing tag with a computer controlled “turtle.”
Another, related example, which appeals enormously to some children with whom we have worked is writing teaching programs. These are like traditional CAI programs but conceived, written, developed and even tested (on other children) by the children themselves.
(Incidentally, this is surely the proper use for the concept of drill-and-practice programs. Writing such programs is an ideal project for the second term of an elementary school course of the sort I shall describe in a moment. It is said that the best way to learn something is to teach it. Perhaps writing a teaching program is better still in its insistence on forcing one to consider all possible misunderstandings and mistakes. I have seen children for whom doing arithmetic would have been utterly boring and alienating become passionately involved in writing programs to teach arithmetic and in the pros and cons of criticisms of one another’s programs like: “Don’t just tell him the right answer if he’s wrong, give him useful advice.” And discussing what kind of advice is “useful” leads deep into understanding both the concept being taught and the processes of teaching and learning.)
Can children do all this? In a moment I shall show some elements of a programming language called LOGO, which we have used to teach children of most ages and levels of academic performance how to use the computer. The language is always used “on-line,” that is to say the user sits at a console, gives instructions to the machine and immediately gets a reaction. People who know languages can think of it as “baby LISP,” though this is misleading in that LOGO is a full-fledged universal language. Its babyish feature is the existence of self-contained sub-sets that can be used to achieve some results after ten minutes of instruction. Our most extensive teaching experiment was with a class of seventh grade children (twelve year olds) chosen near the average in previous academic record. Within three months these children would write programs to play games like the simple form of NIM in which players take l, 2, or 3 matches from a pile; soon after that they worked on programs to generate random sentences—like what is sometimes called concrete poetry—and went on from there to make conversational and teaching programs. So the empirical evidence is very strong that we can do it, and next year we shall be conducting a more extensive experiment with fifth grade children. The next sections will show some of the elementary exercises we shall use in the first weeks of the course. They will also indicate another important aspect of having children do their work with a computer: the possibility of working on projects with enough duration for the child to become personally—intellectually and emotionally—involved. The final section will indicate a facet of how more advanced projects are handled and how we see the effects of the kind of sophistication developed by the children.
5. You Can Take the Child to Euclid, but You Can’t Make Him Think
Let’s go back to Dewey for a moment. Intellectual growth, he often told us, must be rooted in the child’s experience. But surely one of the fundamental problems of the school is how to extend or use the child’s experience. It must be understood that “experience” does not mean mere busy work: two children who are made to measure the areas of two triangles do not necessarily undergo the same experience. One might have been highly involved (e.g., anticipating the outcome, being surprised, guessing at a general law) while the other was quite alienated (the opposite). What can be done to involve the mathematically alienated child? It is absurd to think this can be done by using the geometry to survey the school grounds instead of doing it on paper. Most children will enjoy running about in the bright sun. But most alienated children will remain alienated. One reason I want to emphasize here is that surveying the school grounds is not a good research project on which one can work for a long enough time to accumulate results and become involved in their development. There is a simple trick, which the child sees or does not see. If he sees it he succeeds in measuring the grounds and goes back to class the next day to work on something quite different.
Contrast this situation with a different context in which a child might learn geometry. The child uses a time-shared computer equipped with a CRT. He programs on-line in a version of the programming language LOGO, which will be described in more detail below.
On the tube is a cursor point with an arrow indicating a direction.
The instruction
FORWARD 100
causes the point to move in the direction of the arrow through 100 units of distance. The instruction
ROTATELEFT 90
causes the arrow to rotate 90°.
The child knows enough from previous experience to write the following almost self-explanatory program:
TO CIRCLE
FORWARD 1
ROTATELEFT 1
CIRCLE
END
The word “TO” indicates that a new procedure is to be defined, and it will be called “CIRCLE.” Typing
CIRCLE
will now cause the steps in the procedure to be executed one at a time. Thus:
| 1st Step: | FORWARD 1 | The point creeps ahead 1 unit. |
| 2nd Step: | ROTATELEFT 1 | The arrow rotates 1o. |
| 3rd Step: | CIRCLE | This is a recursive call; naturally it has the same effect as the command CIRCLE typed by the child. That is to say, it initiates the same process: |
| 1st Step: | FORWARD l | The point creeps on, but in the new, slightly different direction. The arrow now makes an angle of 2° with its initial direction. | |
| 2nd Step: | ROTATELEFT | ||
| 3rd Step: | CIRCLE | This initiates the same process all over again. And soon, forever. |
It is left as a problem for the reader to discover why this point will describe a circle rather than, say, a spiral. He will find that it involves some real geometry of a sort he may not yet have encountered (See answer at end of paper.). The more immediately relevant point is that the child’s work has resulted in a
certain happening, namely a circle has appeared. It occurs to the child to make the circle roll? How can this be done? A plan is easy to make:
Let the point go around the circle once.
Then FORWARD 1
Then repeat.
But there is a serious problem! The program as written causes the point to go round and round forever. To make it go just once round we need to give the procedure an input (in more usual jargon: a variable).
This input will be used by the procedure to remember how far round it has gone. Let’s call it “DEGREES” and let it represent the number of degrees still to go, so it starts off being 360 and ends up 0. The way this is written in LOGO is:
| TO CIRCLE:DEGREES | : DEGREES means: the thing whose name is “DEGREES.” |
| IF:DEGREES= O STOP | |
| FORWARD 1 | |
| ROTATE LEFT 1 | |
| CIRCLE:DEGREES – 1 | Each time round the number of degrees remaining is reduced by 1. |
| END |
Now we can use this as a sub-procedure for ROLL:
TO ROLL
CIRCLE 360
FORWARD 10
ROLL
END
Or, to make it roll a fixed distance:
TO ROLL :DISTANCE
IF :DISTANCE = 0 STOP
CIRCLE 360
FORWARD 10
ROLL :DISTANCE 1
END
Or we can make the circle roll around a circle:
TO FUNNYROLL
CIRCLE 360
FORWARD 10
ROTATELEFT 10
FUNNYROLL
These examples will, if worked on with a good dose of imagination, indicate the sense in which there are endless possibilities of creating even more, but gradually more, complex and occasionally spectacularly beautiful effects. Even an adult can get caught up in it! Not every child will. But if he does, the result is very likely to be a true extension of his experience in Dewey’s sense. And evidence is accumulating for the thesis that there is scarcely any child who cannot be involved in some computational project.
The next two sections will discuss two other peripheral devices suitable for a computation laboratory in an elementary school: a programmable vehicle and a music generator. There is, of course, no end to what one could invent. At M.I.T. we are thinking in terms of soon adding mechanical manipulators, psychedelic light shows in a reactive environment, apparatus for automated experiments in animal psychology, etc., etc., etc.
6. The Love of the Turtle
At M.I.T. we use the name “Turtle” for small computer controlled vehicles, equipped with various kinds of sense, voice and writing organs. Turtles can be controlled by the same commands used in the previous section to describe Graphics. They can be made to draw or to move about without leaving a visible trace. Procedures to achieve this are exactly like the procedures for CRT Graphics. However, sense organs allow another interesting dimension of work. An interesting, simple one is a reflectivity sensor held close to the floor. A LOGO operation called “LIGHT” has an integer value between 0 and 10, depending on the reflectivity of the surface. Suppose we wish to program the turtle to follow the left edge of a black line on a white floor. Using an important heuristic we encourage the child to study himself in the situation, and try to simulate his own behavior. The key idea, of course, is to use feed-back according to the following plan:
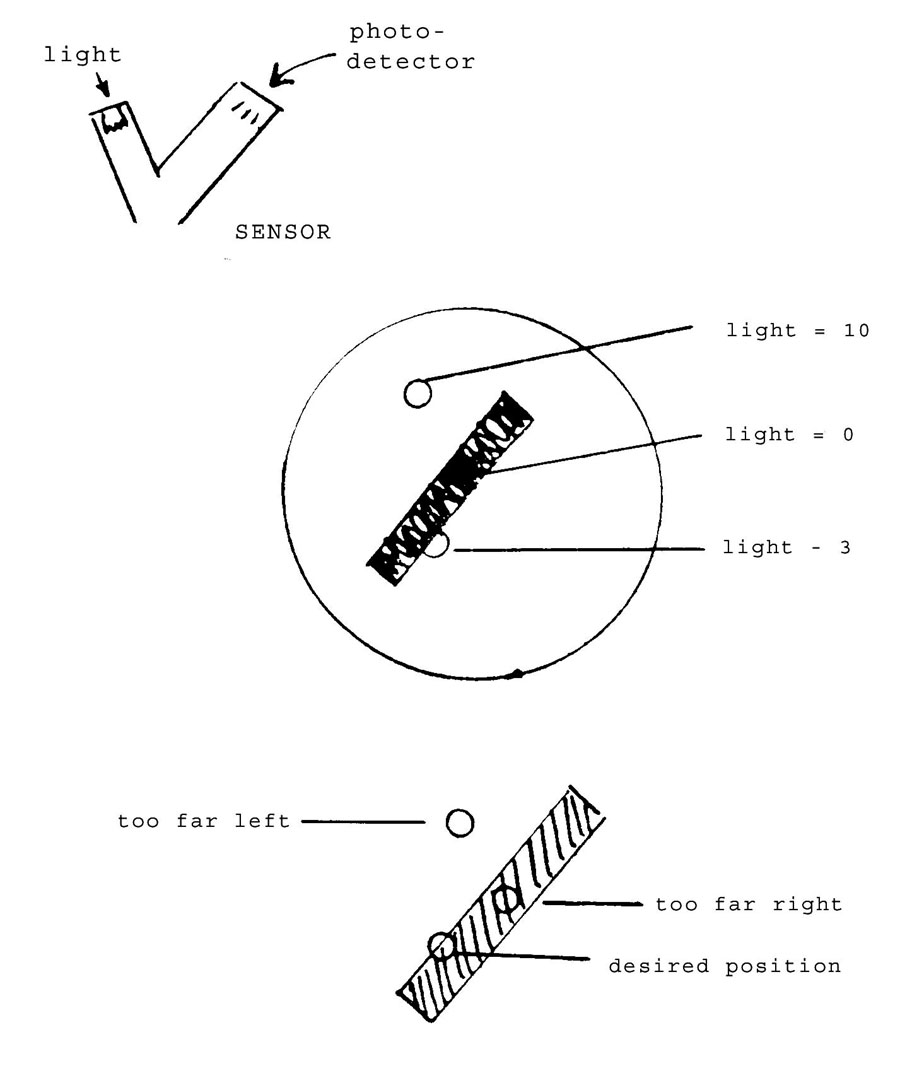
COLOR | LIGHT | POSITION ERROR | CORRECTION |
| Mainly Black | small value | Too far right | ROTATELEFT |
| Equal Black & White | 5 | O. K. | Nothing |
| Mainly White | big value | left | ROTATERIGHT |
This leads to the procedure:
TO WALK
IF LIGHT < 4 ROTATELEFT
IF LIGHT > 6 ROTATERIGHT
FORWARD 1
WALK
END.
Notice that the child can think of the program as a very simple formal model of himself, or, indeed, more justly, of a moth flying to a light. It is rare that children in the traditional context of math-science get a chance to develop a model so simple.
Turtles with touch, interactive behavior with several turtles, searching mazes, and so on scarcely scratch the surface of what can be done with these beasts.
7. Music
Just as the computer can be instructed to move a point on a TV display or make a turtle move or print a word, it can be instructed to sing a note. The LOGO instruction SING can be followed by an input to indicate a note (represented by 1 … 7) or a time. A program can be written thus:
TO MARY
SING 3
SING 2
SING 1
SING 2
SING 3
SING 3
END
The command
MARY
will cause the computer to sing the tune.
The program
TO CHANTMARY
MARY
CHANTMARY
END
will cause the tune to be repeated indefinitely. Programs can be written to speedup, slowdown, raise, lower, transpose, sing in chorus, etc., etc. Children can use the computer as a super musical instrument. They can compose at the typewriter and hear their creations played perfectly. They can make and undo small changes. They can cause the turtle or the CRT display to move to music and so on endlessly.
8. Case Histories from the Muzzey Jr. High School Experiment
The following piece is extracted verbatim from a report on the seventh grade teaching experiment performed at Muzzey Jr. High School at Lexington.
8.1. PROBLEM VS. PROJECT
The most exciting single aspect of the experiment was that most of the children acquired the ability and motivation to work on projects that extend in time over several days, or even weeks. This is in marked contrast with the usual style of work in mathematics classes, where techniques are taught and then applied to small repetitive exercise problems. It is closer, in ways that are essential to the later argument here, to the work style of some art classes where children work for several weeks on making an object; a soapcarving for example. The similarity has several dimensions. The first is that the duration of the process is long enough for the child to become involved, to try several ideas, to have the experience of putting something of oneself in the final result, to compare one’s work with that of other children, to discuss, to criticise and to be criticised on some other basis than “right or wrong.” The point about criticism is related to a sense of creativity that is important in many ways which we shall talk about later—including, particularly, its role in helping the child develop a healthy self-image as an active intellectual agent.
Let’s take an example. A continuing project over the last third of the year was working on various kinds of “language generating” programs. The children studied a program (given as a model) which generated two word sentences like:
CATS RUN
DOGS SHOUT
CHILDREN BITE
DOGS RUN
CATS RUN
.
.
.
The assignment was to study the model and go on to make more interesting programs. The sample printout that follows brought great joy to its creator who had worked hard on mastering the mathematical concepts needed for the program, on choosing sets of words to create an interesting effect and on converting her exceedingly vague (and unloved) knowledge about grammar into a useful, practical form.
INSANE RETARD MAKES BECAUSESWEET SNOOPY SCREAMS
SEXY WOLF LOVES THATS WHY THE SEXY LADY HATES
UGLY MAN LOVES BECAUSE UGLY DOG HATES
MAD WOLF HATES BECAUSE INSANE WOLF SKIPS
SEXY RETARD SCREAMS THATS WHY THE SEXY RETARD
HATES THIN SNOOPY RUNS BECAUSE FAT WOLF HOPS
SWEET FOGINY SKIPS A FAT LADY RUNS
The next class assignment was to generate mathematical sentences which were later used in “teaching programs.” For example:
8 * BOX + 6 = 48
WHAT IS BOX’?
Finally, in the last weeks, someone in the class said she wanted to make a French sentence generator . . . for which she spurned advice and went to work. In the course of time other children liked the idea and followed suit—evoking from the first girl prideful complaints like “why do they all have to take my idea?” The interesting feature was that although they took her idea, they imprinted it strongly with their own personalities, as shown by the following case studies:
K.M. The girl who initiated the project. Thoughtful, serious about matters that are important to her, often disruptive in class. Her approach to the French project was to begin by writing procedures to conjugate all the regular verbs and some irregular ones. The end of the school year fell before she had made a whole sentence generator. But she did have a truly professional program, completely debugged and working with great competence at conjugating—e.g. given VOUS and FINIR as inputs it would reply: VOUS FINISSEZ.
MR A gay, exuberant girl who made the “SEXY COMPUTER” program quoted above. Only half seriously she declared her intention of making the first operational French sentence generator. In a sense she did—but with cavalier disregard for the Academy’s rules of spelling and grammar!
JC A clear mind with a balanced sense of proportion. Deliberately decided to avoid the trap of getting so involved with conjugation that no sentence would ever be generated. Too serious to allow his program to make mistakes. Found a compromise: he would make a program that knew only the third person—but was still non-trivial because it did know the difference between singular and plural as well as the genders: thus it would say
LE BON CHIEN MANGE
but
LES BONNES FILLES MANGENT.
8.2. A DETAIL FROM A CHILD’S MATHEMATICAL RESEARCH PROJECT
The fine texture of the work on projects of this sort can only be shown by case studies. The following vignette needs very little reference to LOGO— thus illustrating how the projects are more than programming.
J is the author of the last French program mentioned. A little earlier he is working on generating equations as part of a project to make “a program to teach 8th grade algebra.” He has perfected a program to generate equations with coefficients in the range of 0-9 using a “random” number generator. His present problem is to obtain larger coefficients.
First Solution: Almost everyone tries this: get bigger numbers by adding smaller ones obtained from the old procedure. Amongst other considerations, this looks like a good technique that has often paid well: use old functions to define new ones.
Consequences: J chooses his equation generator but soon finds some annoying features:
The new coefficients are in the range 0-18, which is unnatural and not very big.
There is a preference for some numbers e.g. 9 conics up ten times as often as 18!
Comment: The first problem can be alleviated by adding more numbers. One can even add a random number of random numbers. But this aggravates the second problem. J understands this qualitatively but does not see a way out. It is interesting that children and adults often have a resistance to making numbers by “non-numerical” operations. In this case the solution is to concatenate the single digit random numbers instead of adding them. LOGO has a simple way to express this and J is quite accustomed to making non-numerical strings by concatenation. In fact this is how he makes the equation! Nevertheless he resists. The problem is discussed in a class meeting and after some prompting everyone suddenly “discovers” the solution.
New Solution: j changes his program, now making numbers up to 99 by concatenation; he does some crude check of uniformity of distribution and tries his program.
Disaster: For a while it seems to go well. But in the course of playing with the “teaching program” a user types 5 and is surprised to get a reply like:
YOU KNUCKLEHEAD; YOU TOOK 11 SECONDS AND YOUR ANSWER IS WRONG. THE ANSWER IS 05. HERE IS SOME ADVICE… etc.
Comment: Poor J will get the sympathy of every mathematician who must at some stage have tried to generalize a result by extending the domain of an innocent looking function only to find that the extended function violates some obscure but essential condition. He is also in the heart of the problem of representation. Is `05″ a good representation? Yes, no . . . have your choice but face the consequences and be consistent. J’s problem is that his procedures accept “05” for arithmetic operations but not for the test of identity!
Solution: Change the identity test or peel off the leading zero, J chose the latter. His program worked for a while and was used to great effect.
New Step: Later J was urged to allow negative numbers. He found a good way: use the one digit random number generator to make a binary decision:
If less than 5, positive
Otherwise, negative.
That Problem Again: J had a program working perfectly with negatives. Then one day decided to make it more symmetrical by using +5 and -5 for positive and negative. This brought him back to the old problems raised by differences between the machine’s representation and the human user’s. At this point the year ended with J’s program not quite as effective as it had been at its peak.
Author Note:
This work was supported by the National Science Foundation under grant number GJ-1049 and conducted at the Artificial Intelligence Laboratory, a Massachusetts Institute of Technology research program supported in part by the Advanced Research Projects Agency of the Department of Defense and monitored by the Office of Naval Research under Contract Number N00014-70-A-0362-0002.
This article originally appeared in: World Conference on Computer Education, IFIPS, Amsterdam, 1970.
![]()