It was with great interest that I recently read Using Technology to Support Prospective Science Teachers in Learning and Teaching About Scientific Models (Cullin & Crawford, 2003). This article presented a convincing argument that the role of models and modeling in science education represented an important and often neglected aspect of investigative science in the classroom. Specifically, the paper presented efforts to engage preservice secondary science teachers participating in a methods course and teaching practicum in modeling experiences ultimately brought to the fore by building and testing dynamic computer models. While the results were mixed, there was a demonstrated shift in the preservice teachers’ views of model use from a teacher-centered use for explaining concepts to a student-centered approach using models to learn about natural phenomena.
This article presents a framework for thinking about the use of models and model-based curriculum in K-12 settings. In doing so, it draws from the work of two colleagues, Leona Schauble and Richard Lehrer, as well as research we conducted together while I was a postdoctoral fellow at The University of Wisconsin and my subsequent work at The University of Texas. The article also proposes that it may be time to look at modeling as a tool that requires both scientific and mathematical reasoning to fully leverage the power of sophisticated thinking by both students and teachers.
There has been a shift in recent years in thinking about mathematics and science instruction. This shift is best exemplified by a transition from pedagogical approaches based on learning facts and procedures to those oriented around constructing, evaluating, and revising models. To be clear, models may be thought of as any number of conceptual entities for the purpose of our discussion. These entities include physical microcosms, representational systems, syntactic models, and hypothetical-deductive models
This pedagogical shift toward modeling entails a number of changes to existing practice, namely, the need to rethink the content that is taught resulting in an emphasis on much more challenging forms of mathematics and science than is typical in K-12 education (Metz, 1995). This change in content creates the need to generate core knowledge about the development of students’ thinking and learning in these new areas of mathematics and science education. This knowledge base then informs the development of curriculum and the day-to-day practice of teachers. These changes are tracked and resolved longitudinally over years, not months or weeks (Lehrer & Schauble, 2001).
Because modeling is central to both mathematics and science (Lehrer, Schauble, Strom, & Pligge, 2001; National Research Council, 1995), one might expect that it would be emphasized from the earliest years of instruction and developed over time, not postponed until high school or beyond. Yet, modeling is not routinely practiced in K-12 schools at all, perhaps because of the persistence of theories of education and evaluations focusing on simple, component skills for young children and a graduation to complex forms of reasoning only for older and more capable students (Bruer, 1993; Collins, Brown, & Newman, 1989; Schauble, Glaser, Duschl, Schulze, & John, 1995). Or, perhaps just as likely, this results because of the lack of existing information to guide teachers in how to engage children in complex forms of scientific and mathematical thinking and reasoning. Whatever the specific reasons for the paucity of modeling in the K-12 curriculum and in teacher training, it is widely agreed that good instruction should proceed in accord with the development of children’s understanding (Carpenter & Lehrer, 1999).
Modeling as Representation and Inscription
One of the foundational pillars of a modeling perspective is the belief that early reasoning about models is anchored in children’s invention and use of a broad variety of representational devices, such as maps, data displays, drawings, or photographs. Collectively, these are known as inscriptions (Latour, 1990; Lehrer & Schauble, 2000) because they involve writing , drawing, or some other form of symbolization of the external world of the student. Inscriptions stem from an even more fundamental capacity regarding one thing as representing or standing for another. These early forms of representational competence with inscriptions comprise the foundation and leverage point for model-based reasoning.
Modeling contains more than simply inscriptions. For instance, modeling contains the self-conscious separation by the learner of a model from its referent. This is surely central to the kinds of modeling practiced by scientists and mathematicians, even though novice students tend to blur these distinctions (Petrosino, 1998; Schauble et al., 1995). This is also known as “models as copies” and was demonstrated quite well in studies by Grosslight and colleagues (Grosslight, Unger, Jay, & Smith, 1991).
Another aspect of modeling is that children do not consider the possibility of measurement error. They often get disconcerted when they find a discrepancy between the expected value of a measure and its observed value. Moreover, given its centrality to core scientific and mathematical ideas (e.g., evolution), variability is given short, if any, attention in school instruction. Students are given few conceptual tools to reason about variability, and even if they are, the tools are rudimentary, at best. Typically, these tools consist only of brief exposure to a few statistics (e.g., for calculating the mean or standard deviation), with little focus on the more encompassing sweep of data modeling (Lehrer & Romberg, 1996). That is, students do not typically participate in contexts that allow them to develop questions, consider qualities of measures and attributes relevant to a question, and then go on to structure data and make inferences about their questions (Petrosino, Lehrer, & Schauble, 2003).
Third, it appears to be challenging for young students to develop the understanding, based on analogy of residual or mismatch between the model and the world (Grosslight et al., 1991), that alternative models are possible and may be preferable to the ones currently being entertained. Finally, other than scientists and mathematicians, few people in society are typically aware of the role rival models play in evaluating alternative hypotheses. This has serious implications when it comes to both the understanding of rival models in teacher education and in the K-12 curriculum.
Pedagogical Implications
While it is fine to cite the importance of models and model-based reasoning, what is needed is a way to think systematically about the pedagogical implications for such a method of curriculum. In order to build critical standards about representational choices, teachers need a history of experience with fixing and composing representations in inscriptions and notations used as matters of convention for communicating and supporting the reasoning of a practicing community (Lehrer & Schauble, 2000). At the core of this process must be the understanding that modeling needs to be practiced systematically, so that over time the forms and uses of a variety of models are explored and evaluated for a range of purposes.
Model-based reasoning can be thought of as a continuum in which teachers begin with children’s basic representational capacities and try to end up near the practices of mathematicians and scientists. In the middle is an intermediate form of representation and modeling. The teacher’s role then becomes one of a bridge between the child’s world and the more scientifically developed world of the content experts (in this case, mathematicians and scientists). This puts a stress on teachers since they must be masters of two worlds. The first world is the world of children with their preconceptions and naïve and experiential notions of the world. The second world is that of the “scientist,” with the development of abstractions, symbolism, and analogical reasoning. The teacher who transverses a world with which pedagogical content knowledge (Schulman, 1987) and domain expertise are paramount must be an effective medium between the two. Therefore, teaching in a model-based manner requires a good understanding of children’s thinking, in order to ensure that pedagogy builds systematically on a base of understanding. It is just as important, however, that teaching be informed by a long-term view needed to navigate these early competencies into forms of thinking that are complex, multifaceted, and unfolding over yearsnot weeks or months. Such a commitment to modeling suggests the value of addressing early some forms of mathematics and science concepts not typically taught until later in a student’s education, if ever at all.
A Developmental Taxonomy of Models
At root, a model is an analogy. Something familiar stands in for something unfamiliar, like water for electricity. At issue is the nature of the relationship between the model and the world. Gentner (1983) and Gentner and Toupin (1986) proposed a continuum of instructional models that may be helpful (see Figure 1 and Table 1). At one end is similarity, which invokes whole-scale correspondence between relations and literal attributes. At the other end is analogy, which succeeds when a system of relations in one domain is aligned with a system of relations in a second domain.
Although this modeling taxonomy is consistent with educational theory about the development of analogical reasoning in children, it holds the status of a design hypothesis. The importance of this hypothesis is that it will be most fruitful to introduce children to modeling practices through models that preserve resemblance, because these models more readily sustain mappings between the model and the world. As children learn over a number of cases that resemblance is less fundamental than function, they become increasingly prepared to work with models that do not preserve similarity between the model and the modeled world. Moreover, as suggested by Lehrer and Schauble (2000), emphasizing the historical trend toward the mathematization of science captures an important pedagogical principle: The cognitive move toward functional description (i.e., analogy; relational structure) is provoked and sustained by having mathematical resources at one’s disposal.
Mathematical Tools for Effective Modeling
Navigating a modeling curriculum requires that students have mastery of mathematical tools. Traditionally, the mathematics taught in elementary school in the United States has almost exclusively emphasized number and computation. Yet, mathematics reform leaders, such as the National Council of Teachers of Mathematics (NCTM), have been prescribing a wider view of mathematics, one that accords much better with an emphasis on modeling. The NCTM standards (1991) suggest that the mathematics of geometry, probability, and data should be introduced much earlier and in an integrated fashion, not postponed until high school and then presented as self-contained courses providing little or no contact with students’ other mathematical knowledge and perhaps even less with students’ mathematical sense-making.
To fully address a modeling perspective, teachers need to develop appropriate mathematical models to make sense of the world. While there well may be any number of critical mathematical concepts and associated abilities, Lehrer and Schauble (2000) identified four (Space and Geometry, Data, Measure, and Uncertainty and Probability) as significant leverage points by which teachers can bring modeling into the child’s world. A few short examples of each follow.
Space and Geometry
Students need to be able to mathematize three dimensional space in order to study such phenomena as diversity of microinvertabrates in a local stream, to map heights of model rocket launches in the local schoolyard (Petrosino, 1998), or to think about core concepts like density, which makes little sense without a significant sense of volume. Furthermore, the properties of geometrical figures like triangles (i.e., trigonometry functions) are useful for understanding a variety of phenomena ranging from calculating the height of a model rocket launch to the length of shadows to rates of change expressed on a graph (Lehrer & Schauble, 2000).
Data
The concept of data encompasses a number of issues for the teacher, including the construction of relationships between common, familiar cases to the child’s world and more general global patterns of which the cases are a component (Hancock, Kaput, & Goldman, 1992; Schauble et al., 1995). Teachers need to allow students to come to the realization that one can manipulate data to ask novel questions that can be usefully addressed (Lehrer & Romberg, 1996). Furthermore, a key aspect of this mathematical model is bringing to the fore the importance of data representations and data interpretation, as well as problems of sampling, measurement error, and ideas about central tendency and variability, which are fundamental to modeling (Mokros & Russell, 1995; Petrosino et al., 2003).
Measure
Teachers need to work deliberately to assist students in the development of a consistent and disciplinarily rich theory of measure. It is usual for teachers to focus exclusively on procedures for measuring since this is the emphasis in many textbooks and curricula objectives. Using a more student-centered approach, students can discover which properties of measure need to be emphasized in measuring some attribute. What is critical, however, is not applying instruments such as rulers, but coming to understand some rather fundamental ideas not necessarily obvious to children. One such idea holds that measure incorporates ideas such as iteration, origin, and equal units (Lehrer, Jenkins, & Osana, 1998). Moreover, measuring helps students progress in thinking about such traditionally scientific ideas as force, speed, and time by mathematizing them. When children work with data there is often much struggle over deciding what should count as a valid measure of the variables of interest (Petrosino, 1998).
Probability and Uncertainty
Uncertainty is at the pivot point of certain scientific phenomena such as evolution, genetic inheritance, and atomic theory and plays a somewhat more limited role in many others (Lehrer & Schauble, 2000). For example, the behavior of migrating birds can be modeled by specifying the simple rules that participating members follow, but these rules often include an element of randomness. While there is a body of research on children’s understanding of uncertainty and probability (Fay & Klahr, 1996), there is a paucity of research that investigates how these ideas develop in the context of real classrooms. Initial investigations in this area indicate that understanding the mathematical implications of these ideas is difficult. For instance, elementary school children have a tendency to regard some events that are actually probabilistic as deterministic. One example of this is the work of Horvath and Lehrer (1998), who determined that children found constructing the notion of a sample space and then evaluating observed outcomes against that model to be challenging (e.g., “Three is my lucky number, so I think I’ll get mostly threes”). When the observed outcomes do not match the sample space, children are liable to generate causal interpretations to account for the deviations.
These four important mathematical ideas are the foundation for creating and maintaining a modeling approach to instruction. Likewise, these ideas are essential to both mathematics and science and, consequently, point out the connections between these two disciplines. Geometry, measure, data, and probability conceptually intersect at many points. Understanding how children think about these concepts, how teachers teach these ideas, and how technology can support these processes is the major goal of a number of researchers in the field.
In the same manner, the developmental taxonomy of models proposed by Gentner (1983) and subsequently elaborated upon gives us a firm theoretical foundation on which to consider how to introduce models in the K-12 curriculum. Technology has and will continue to play a vital role in the process of incorporating modeling into K-12 instruction (Jonassen, 2003). However, here needs to be a firm foundation and developmental trajectory for children’s understanding in these areas of mathematics and science education. What models should be used? When? What are the affordances and limitations of various models? This manuscript, along with the applied work of Cullin and Crawford, contributes to the ongoing dialogue.
References
Bruer, J. (1993). Schools for thought: A science of learning in the classroom. Cambridge, MA: MIT Press.
Carpenter, T. P., & Lehrer, R. (1999). Teaching and learning mathematics with understanding. In E. Fennema & T. R. Romberg (Eds.), Mathematics classrooms that promote understanding (pp. 19-32). Mahwah, NJ: Lawrence Erlbaum .
Collins, A., Brown, J. S., & Newman, J. E. (1989). Cognitive apprenticeship: Teaching the crafts of reading, writing, and mathematics. In L. B. Resnick (Ed.), Knowing, learning, and instruction (pp.453-494). Hillsdale, NJ: Lawrence Erlbaum Associates.
Cullin, M., & Crawford, B. A. (2003). Using technology to support prospective science teachers in learning and teaching about scientific models . Contemporary Issues in Technology and Teacher Education [Online serial], 2(4). Available: https://citejournal.org/vol2/iss4/science/article1.cfm
Fay, A. L., & Klahr, D. (1996). Knowing about guessing and guessing about knowing: Preschoolers’ understanding of indeterminacy. Child Development, 67, 689-716.
Gentner, D. (1983). Structure-mapping: A theoretical framework for analogy. Cognitive Science, 7, 155-170.
Gentner, D., & Toupin, C. (1986). Systematicity and similarity in the development of analogy. Cognitive Science, 10, 277-00.
Grosslight, L., Unger, C., Jay, E., & Smith, C. L. (1991). Understanding models and their use in science: Conceptions of middle and high school students and experts. Journal of Research in Science Teaching, 29, 799-822.
Hancock, J., Kaput, J. J., & Goldsmith, L. T. (1992). Authentic inquiry with data: Critical barriers to classroom implementation. Educational Psychologist, 27, 337-364.
Horvath, J., & Lehrer, R. (1998). A model-based perspective on the development of children’s understanding of chance and uncertainty. In S. P. LaJoie (Ed.), Reflections on statistics: Agendas for learning, teaching, and assessment in K-12 (pp. 121-148). Mahwah, NJ: Lawrence Erlbaum.
Jonassen, D. H. (2003). Using cognitive tools to represent problems. Journal of Research on Technology in Education 35(3), 362-381.
Latour, B. (1990). Drawing things together. In M. Lynch & S. Woolgar (Eds.), Representation in scientific practice (pp.19-68). Cambridge, MA: MIT Press.
Lehrer, R., Jenkins, M., & Osana, H. (1998). Longitudinal study of children’s reasoning about space and geometry. In R. Lehrer & D. Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 137-168). Mahwah, NJ: Lawrence Erlbaum.
Lehrer, R., & Romberg, T. (1996). Exploring children’s data modeling. Cognition and Instruction, 14, 69-108.
Lehrer, R., & Schauble, L. (2000). Modeling in mathematics and science. In Robert Glaser (Ed.), Advances in instructional psychology. Educational design and cognitive science. Mahwah, NJ: Lawrence Erlbaum.
Lehrer, R., Schauble, L., Strom, D., & Pligge, M. (2001). Similarity of form and substance: Modeling material kind. In S. Carver & D. Klahr (Eds.), Cognition and instruction: Twenty-five years of progress. Mahwah, NJ: Lawrence Erlbaum.
Metz, K.E. (1995). Reassessment of developmental constraints on children’s science instruction. Review of Educational Research, 65, 93-127.
Mokros, J., & Russell, S. R. (1995). Children’s conceptions of average and representativeness. Journal of Research in Mathematics Education, 26, 20-39.
National Council of Teachers of Mathematics. (1991). Professional standards for teaching mathematics . Reston, VA: Author.
Petrosino, A. J. (1998). At-risk children’s use of reflection and revision in hands-on experimental activities. Dissertation Abstracts International-A, 59(03). (UMI No. AAT 9827617).
Petrosino, A. J., Lehrer, R., & Schauble, L. (2003). Structuring error and experimental variation as distribution in the fourth grade. Mathematical Thinking and Learning, 5(2&3), 131-156.
Resnick, M. (1995). Turtles, termites, and traffic jams. Cambridge, MA: MIT Press.
Schauble, L., Glaser, R., Duschl, R. A., Schulze, S., & John, J. (1995). Students’ understanding of the objectives and procedures of experimentation in the science classroom. The Journal of the Learning Sciences, 4, 131-166.
Shulman, L. S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57, 1-22.
Acknowledgement
This work was supported by the following: National Science Foundation grant (14656-S1 Amendment 4) entitled Challenges to Projects: VaNTH K-12 Partners in Education and a grant from the Department of Education (DOE P342A000111) entitled (Inventing New Strategies for Integrating Technology in Teacher Education (Project INSITE) additional support was made possible by The University of Texas at Austin’s Dean’s Faculty Fellowship Program under the direction of Dean Manuel J. Justiz and Larry Abraham. I would like to thank Richard Lehrer and Leona Schauble for their invaluable mentorship during my postdoctoral studies at The University of Wisconsin. Thanks also to Cathy Loving and Carol Stussey for their comments and suggestions on earlier drafts and a final special thanks goes to Jennifer Cook for her editorial assistance.
Contact Information:
Anthony J. Petrosino
Department of Curriculum and Instruction
Science and Mathematics Education Center
E-mail [email protected]
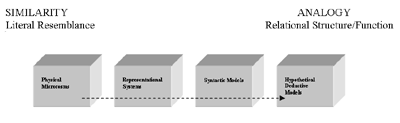
Figure 1. A Developmental Trajectory for Models Used in Instruction
Table 1. A Developmental Taxonomy of Models
| TYPE OF MODEL | EXAMPLE | INSTRUCTIONAL USES |
| Physical Microcosms | Model the world via resemblance | Models of the solar system, planetarium models of the cosmos, terrarium models of ecosystems, model rockets |
| Representational Systems | Maps, diagrams, and related display notations | These preserve an intermediate degree of resemblance between the model and the world. Nevertheless, extended work with them fosters understanding of the need for symbolic conventions to make the relation between the model and the world more explicit. |
| Syntactic Models | Exchange similarity for analogy; the model and the world are in a relational correspondence that is not sustained by resemblance | The power of syntactic models resides in their ability to summarize the essential functioning of a system. This form of modeling is apt to be challenging for children, because it deprives them of easy ways to establish correspondence between the representing and the represented world. Nevertheless, resemblance is never a sufficient condition for modeling. |
| Hypothetical-Deductive Models | These models move beyond the realm of describing the observable to embodying unseen hypothetical entities that interact to produce emergent behavior | These models incorporate mechanisms that can produce previously unseen and often unpredicted behaviors. (Gas Model). This form of modeling is especially difficult since there is no direct connection between any single hypothetical entity and the observed world and partly because the idea of emergence may prove problematic for people of any age (Resnick, 1995). |
![]()