
2021 NTLI Award Paper in Mathematics Education
Teaching is extremely complex. In every lesson teachers make thousands of decisions. Fundamental to those decisions is their taking in information about what is happening in the classroom at the moment — otherwise known as teacher noticing (Jacobs & Spangler, 2017). One way to support the development of teacher noticing is to provide teachers with frameworks to help guide their noticings and ultimately their decision making.
The literature is rich with examples of the ways in which frameworks have supported preservice teachers learning to notice in mathematics classrooms. For example, Mitchell and Marin (2014) used an analysis framework to support preservice teachers noticing important aspects of mathematics, while Teuscher et al. (2017) used a framework to support preservice teachers noticing mathematically significant pedagogical opportunities.
When students are working in technology-mediated learning environments (i.e., working on technology-enhanced mathematics tasks), the practice of teacher noticing is more challenging because teachers must pay attention not only to what students say or write but also to ways the technology contributes to student understanding (e.g., Chandler, 2017; Lovett et al., 2019; Walkoe et al., 2017; Wilson et al., 2011).
Walkoe et al. (2017) noted this challenge and the need to support teachers in learning to “look for key student thinking practices … through the lens of technology-mediated student work” (p. 67). Because of this additional complexity, this study sets out to investigate the ways in which preservice teachers engaged in noticing students’ mathematical thinking in technology-mediated learning environments when introduced to a framework intended to support this noticing of students’ thinking.
Background Literature
To situate this work, we first drew from relevant literature on preservice teacher noticing of students’ mathematical thinking. We share here frameworks that have supported teachers in their development of teacher noticing and discuss teacher noticing within technology-mediated learning environments.
Preservice Teacher Noticing
Jacobs and Spangler (2017) described teacher noticing as “focusing attention on and making sense of what students do before actually responding to them” (p. 771). Teacher noticing is grounded in the work of Mason (2002), who stated that “every act of teaching depends on noticing: noticing what children are doing, how they respond, evaluating what is being said or done against expectations and criteria, and considering what might be said or done next” (p. 7). There is much to notice within a classroom. Due to this complexity, the importance of noticing students’ mathematical thinking is emphasized in the Association of Mathematics Teacher Educators’ (2017) Standards for Preparing Teachers of Mathematics:“Well-prepared beginners commit themselves to noticing, eliciting, and using student thinking to assess student progress in understanding the mathematics and to adjust instruction in ways that further support and advance learning toward the intended learning goals” (p. 16).
When studying teacher noticing, conceptualizations depend on the particular focus; are teachers noting everything they deem important within a lesson or are teachers noticing specific instances of student interactions or student thinking for a particular subject (Philipp et al., 2014)? For the purposes of this study, we draw upon Jacobs et al.’s (2010) conceptualization of teacher noticing of students’ mathematical thinking, which comprises three interrelated skills: attending to students’ strategies, interpreting their understanding, and deciding how to respond on the basis of those understandings.
Since noticing is such an important practice, much research has been completed studying teacher noticing of student thinking in various mathematical contexts, ranging from elementary preservice teachers’ noticing student’s early numeracy skills (Schack et al., 2013) to secondary preservice teachers’ noticing students’ statistical understanding of a line of best-fit task (Nagel et al., 2020). When working with developing preservice teachers’ noticing, various artifacts of student work have been considered. According to Jacobs and Spangler (2017) video cases are the most common choice (e.g., Jong et al., 2021; Krupa et al., 2017), but other artifacts include student written work (e.g., Dick, 2017), transcripts of student conversations (e.g., Dreher & Kuntze, 2015) or combinations of the two (e.g., Ivars et al., 2020). Regardless of the type of artifact, a commonality between these studies is a desire to help preservice teachers improve their noticing skills through exposure to student thinking.
Results considering improvement of preservice teacher noticing have been mixed (Amador et al., 2021). Noting simultaneously all aspects of student thinking is often difficult for preservice teachers. Despite the difficulty, one method that has shown some success in supporting preservice teachers’ noticing has been through decomposing the practice (Grossman et al., 2009) through frameworks that break aspects of teacher noticing into component parts.
Use of Frameworks
The importance of integrating frameworks into preservice teacher education is emphasized in the Association of Mathematics Teacher Educators’ (2017) Standards for Preparing Teachers of Mathematics:
An effective mathematics teacher preparation program ensures that practice-based experiences, including mathematics methods courses and equivalent learning experiences, provide candidates with experiences using tools and frameworks grounded in research to develop core pedagogical practices and pedagogical content knowledge for teaching mathematics. (p. 35)
In line with this advice, researchers have studied how incorporating frameworks has supported preservice teacher noticing. For example, Ivars et al. (2020) provided preservice teachers (PTs) with a learning trajectory framework for the fraction concept to guide their noticing and found that the learning trajectory “provided PTs with a guide to talk about students’ mathematical understandings” (p. 543) and ultimately acted as a scaffold to support their noticing.
In contrast, Moreno et al. (2021) provided preservice teachers with a learning trajectory they described as “research-based frameworks of children’s thinking” (p. 57) with an expressed goal of developing their noticing. They studied the ways in which the preservice teachers used the learning trajectory to notice students’ thinking of measurement and found the complexity of the learning trajectory was too much for the preservice teachers and did not lead to increased noticing. These studies show the need for careful selection of frameworks accessible to preservice teachers.
Additional frameworks have been used in an attempt to scaffold the noticing practice. For example, Stockero and colleagues shared frameworks related to high-leverage instances of students’ mathematical thinking and found they supported their noticing of mathematically significant pedagogical opportunities (MOST framework; Leatham et al., 2015; Stockero & VanZoest, 2013). Their most recent work showed the transferability of preservice teacher noticing using the MOST framework over time from coursework to student teaching experience (Stockero, 2020).
Though not only focused on teacher noticing, Santagata and Yeh (2016) provided preservice teachers with the Lesson Analysis Framework to guide their analysis of video cases, for which one aspect was attending to student mathematical thinking. They found that the framework supported the preservice teachers’ analysis. Similarly, Mitchell and Marin (2015) provided the Mathematical Quality of Instruction (MQI) framework as a scaffold for preservice teachers’ noticing of salient features of classroom practice — one of which was noticing student thinking. They found that, while it took time for the preservice teachers to fully understand and apply the framework, overall “the MQI as an analysis framework supported participant ability to notice student thinking” (p. 573).
In addition, Fisher et al. (2019) and Dick et al. (2021) provided Jacobs et al.’s (2010) framework as part of preservice teacher instruction with the express goal of helping preservice teachers focus on the differences between the three components of noticing. Fisher et al. began with the attend component and slowly developed preservice teachers’ noticing to next interpret and finally make instructional decisions. They found this process led to increases in preservice teacher attending and interpreting, but concluded, “The deciding component increases when the complexity increases” (p. 148).
Given the promise of providing frameworks as a way to support the practice of preservice teacher noticing, for this study, we provided preservice teachers with a framework based on Jacobs et al. (2010) and adapted to include noticing students’ thinking in technology-mediated learning environments.
Technology-Mediated Learning Environments
In their synthesis of research on teacher noticing, Amador et al. (2021) noted that results show the practice of teacher noticing can be complex, especially for preservice and novice teachers. Teacher noticing gains additional complexity when students are working in technology-mediated learning environments. In such environments students use technologies “that can perform mathematical tasks and/or respond to the user’s actions in mathematically defined ways” (Dick & Hollebrands, 2011, p. xii).
With these technologies, students can interact with objects through dragging and dynamically view the resulting changes (e.g., Desmos Graphing Calculator and GeoGebra). Research on these technologies has shown that they can help mediate student’s mathematical thinking (e.g., Arzarello et al., 2002; Baccaglini-Frank & Mariotti, 2010; Trouche & Drijvers, 2010).
For example, Baccaglini-Frank and Mariotti (2010) studied high school students and asked them to conjecture about geometric shapes while exploring an open problem in a dynamic geometry environment. They found that noticing the students’ dragging schemes elucidated the students’ mathematical thinking. Similarly, Arzarello et al. (2002) found the way a student used the dynamic representations in Geometer’s Sketchpad to solve a problem revealed insight to their mathematical thinking. Both Baccaglini-Frank and Mariotti and Arzarello et al. commented on the usefulness of examining students’ technology engagement, which demonstrates the importance of the role of technology engagement when noticing students’ thinking in such environments.
Research into the ways teachers notice students’ mathematical thinking when they are working in technology-mediated learning environments is limited (e.g., Chandler, 2017; Wilson et al., 2011; Yeo & Webel, 2019). Chandler researched how preservice teachers noticed students’ thinking with written artifacts vs. technology-mediated artifacts and found that, overall, preservice teachers ignored the role of the technology in developing the students’ understanding and instead noticed similarly across the two task mediums.
More recently, Yeo and Webel (2019) asked preservice teachers simultaneously to evaluate a dynamic mathematics technology and notice students’ thinking within a technology-mediated environment. They found that having preservice teachers first work with the technology helped them interpret student’s thinking related to “how students solved the task and how they engaged with different [dynamic] representations” (p. 1052) and assisted them in their evaluation of the technology itself.
In our previous work, we studied preservice teacher noticing of students’ thinking in technology-mediated learning environments and found that not explicitly asking preservice teachers to notice the ways students engaged with the technology hindered their noticing (Lovett et al., 2019). Such findings illuminate the potential benefit preservice secondary mathematics teachers (PSMTs) may draw from explicit scaffolding on noticing student thinking within technology-mediated learning environments and led to this study that questions how a framework focused on noticing students’ mathematical thinking in such environments may support preservice teacher noticing.
Conceptual Framework
We framed this work using a framework for Noticing of Students’ Mathematical Thinking in Technology-Mediated Learning Environments (NITE; Bailey et al., 2021; Dick et al., 2021) as a means to support preservice teacher noticing. The NITE framework is an adaptation of Jacobs et al.’s (2010) professional noticing of students’ mathematical thinking framework.
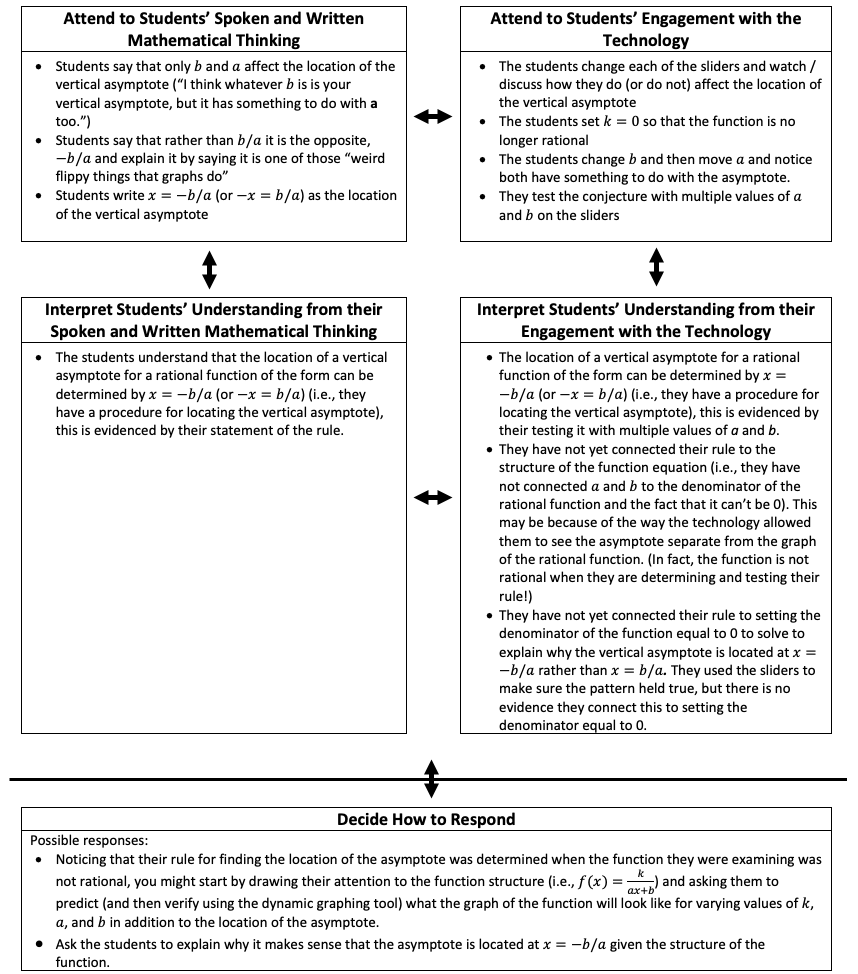
The NITE framework (Figure 1) acknowledges that all components of noticing are by their nature interrelated (Jacobs et al., 2010). The separation of “attention to and interpretation of students’ spoken and written mathematical thinking” from “attention to and interpretation of students’ engagement with the technology” is to highlight the importance of including the actions students take with the technology and see the results of these actions when attending to and interpreting students’ mathematical thinking. Thus, the arrows in the NITE framework indicate the importance of both the horizontal coordination of attention and interpretation as well as the vertical integration of both attention and interpretation. The “decide how to respond” component is separated from the other components for two reasons: (a) to indicate the importance of balancing insight gained from attending to and interpreting both students’ spoken and written mathematical thinking and their technology engagement when making instructional decisions and (b) when deciding how to respond, teachers must consider how to position the technology (or not) in their response to support the student in moving forward.
Figure 1
Teacher Noticing of Student’s Work in a Tool-Mediated Learning Environment (The NITE Framework; Bailey et al., 2021; Dick et al., 2021)

To illustrate the coordination articulated by the NITE framework, an example is provided here that we will return to later in this paper. Consider a dynamic exploration task in which students were being introduced to the idea of a vertical asymptote. In this Desmos task, students used sliders to explore the parameters of rational functions and their effect on the number of vertical asymptotes a function has and their location. Students explored more complex rational functions as they moved through the activity (see Figure 2). At the end of the activity, students were asked to respond to the following questions:
- Based on what you have learned, how could you explain to a friend how to determine the number of vertical asymptotes a rational function might have?
- How would you explain how to find the location of those vertical asymptotes given the rational function?
Imagine monitoring students as they are working in pairs on the activity. One pair, Eden and McKenzie (these are pseudonyms), used sliders to explore the parameters k, a, and b in the function
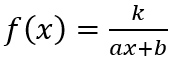
and their effect on the location (and existence) of vertical asymptotes. A detailed transcript of what they did and said while they worked is provided in Figure 3.
Figure 2
Snapshot of the Vertical Asymptote Desmos Activity
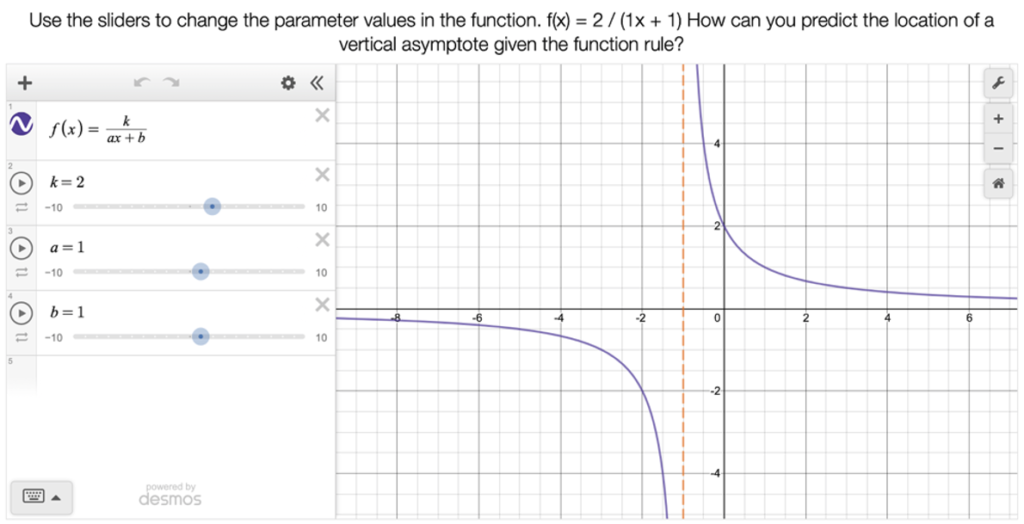
Figure 3
Transcript of Eden and McKenzie Working on the Vertical Asymptote Desmos Activity

See Appendix for text version of transcript
Paying attention to what the students say, it is apparent that they have determined a way to find the location of a vertical asymptote for rational functions of the form in question. However, using the NITE framework to guide noticing, in the attend and interpret components of noticing in a technology-mediated learning environment, teachers should go beyond what they hear students say or see them write, and also consider their engagement with the technology. Doing this carefully might result in the noticing shown in Figure 4. Ultimately, the NITE framework highlights both the thinking that students can express through their technology engagement and what teachers can learn about their thinking by attending to it and, therefore, scaffolds the practice to support PSMTs focusing on all components.
Figure 4
Example of the NITE Framework
Methods
This study was situated within the context of a larger project that is creating a series of modules for mathematics teacher educators to use with PSMTs to examine secondary students’ mathematical practices. We aimed to answer the following research question: How does explicitly sharing the NITE framework and providing opportunities for practice during a single course support PSMTs’ engagement with the individual noticing skills of attending to and interpreting students’ mathematical thinking in technology-mediated environments as well as their coordination of the two?
Participants
This study was situated in a course focused on teaching secondary mathematics with technology at a university in the southeast United States that occurred in spring 2020. The earlier portion of the course was carried out in person, and the latter was carried out remotely (a mixture of synchronous and asynchronous online settings) due to the COVID-19 pandemic. While the transition to a virtual setting in the middle of the semester did change the structure of some of the course materials, it did not change the content of the course materials or plans for data collection.
Eight of nine PSMTs enrolled in the course agreed to participate in the study. Unlike the typically female dominated population of U.S. teachers (National Center for Education Statistics, 2020), our group of PSMTs was evenly distributed across the gender binary (50% female identifying, 50% male identifying, 0% other). At the time of the study, all participants had successfully completed coursework at least through Calculus 2, were mathematics majors and secondary mathematics education minors, and were preparing to be high school mathematics teachers. The participants are referred to in this article using codes (i.e., PSMT 1). Additionally, we chose to use gender neutral pronouns (i.e., they/them), as our goal is not to highlight any similarities or differences across gender identification categories.
Context of This Study
To support PSMTs in their development of the practice of noticing students’ mathematical thinking in technology-mediated learning environments, we are in the process of designing curriculum materials that use the NITE framework and video cases of secondary students to deepen teachers’ understanding of students’ mathematical thinking while engaged in technology-mediated tasks. Guided by the tradition of design research in curriculum development (e.g., Clements, 2007; Cobb et al., 2003), we are engaging in cycles of refinements based on feasibility and pilot testing of the materials as they are being developed.
The first module introduced the NITE framework. PSMTs were provided with a 3-minute video clip of a pair of secondary students engaged in a Desmos activity, in which they used sliders to explore the parameters of a quadratic function in vertex form — that is, f(x) = a(x – h)2 + k. This clip was focused on the students’ exploration of parameter h. PSMTs watched the video and then were asked to attend to and interpret the students’ thinking. Next, each of the components of the NITE framework and the importance of coordinating among them were discussed in class. PSMTs then watched the same clip again and refined their attend and interpret responses.
As a whole class, we built upon the work of the small groups and created what we agreed were robust attend and interpret responses — fully coordinating students’ written and spoken mathematical thinking along with the ways they engaged with the sliders to describe and make sense of the effect parameter h has on the graph of the function. We wrapped up the module by sharing tips for effective attending and interpreting. Additionally, we discussed Thomas et al.’s (2015) conceptualization of how the practice of noticing students’ mathematical thinking is foundational to the Five Practices for Orchestrating Productive Mathematics Discussions (Smith & Stein, 2018), providing the bigger picture of what we were building toward across this course and others in the program.
In addition to this introductory module, the project aims to develop six additional modules, each with a different mathematical focus. At the time of this study, tasks for four modules had been developed and were being piloted. The design of these tasks was guided by our design principles for examining student practices in technology-mediated learning environments (Lovett et al., 2020). Mathematical topics in the four modules included the concept of function, rate of change, and function families.
In each module, PSMTs examined carefully selected video clips of pairs of secondary students working together on technology-based tasks (e.g., Desmos and GeoGebra). The question prompts that accompanied the videos were guided by the NITE framework, often beginning with a focus on attending and interpreting students’ thinking and later adding other practices that build on noticing (e.g., questioning, predicting, selecting, sequencing, and connecting). For example, one of the tasks was in the context of a Desmos activity named Function Carnival. PSMTs had completed the Function Carnival task in a prior lesson.
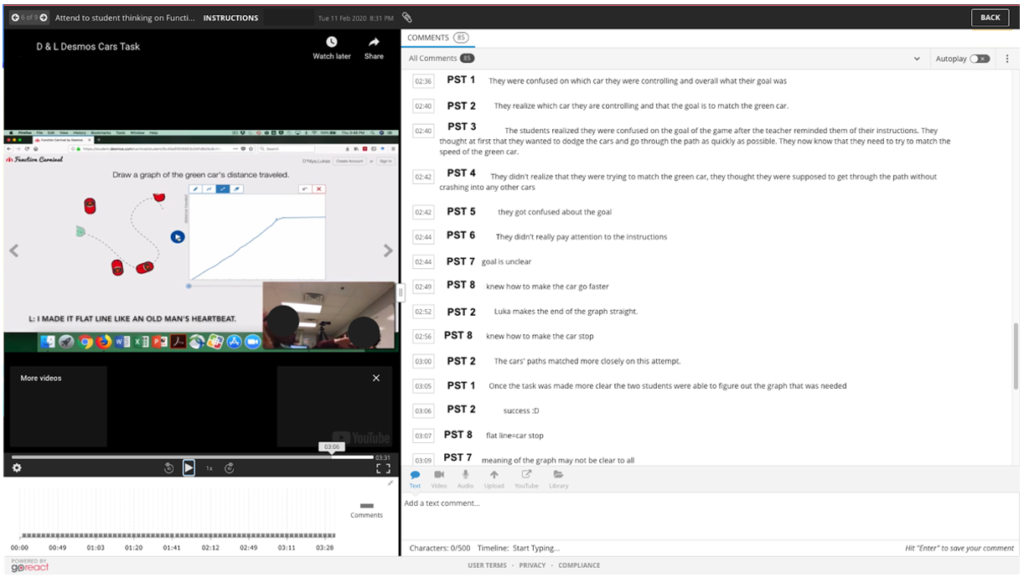
Here, PSMTs watched a video of a pair of students working on a portion of the activity in which they were to draw the time vs. distance traveled graph for a car that was traveling along a curvy road. PSMTs collaborated in an interactive platform (i.e., GoReact) to tag moments in the video that they thought were mathematically important given the learning goals (see Figure 5). Next, PSMTs were asked to write up their interpretations of the students’ current understandings related to the learning goals (i.e., describing qualitatively the functional relationship between two quantities by analyzing a graph, describing qualitatively the functional relationship between quantities by analyzing a simulation of their interaction, and sketching a graph that exhibits the features of a function described through a simulation of the resulting action). While only a subset of the modules was piloted at this time, additional video-based tasks were used with the PSMTs throughout the semester in similar ways. These tasks included examining small groups of students working on technology-based geometry and statistics tasks.
Figure 5
PSMTs Collaborate to Attend to Students’ Mathematical Thinking on a Desmos Activity
Data Sources and Collection
To evaluate the usefulness of introducing the NITE framework to PSMTs, we created an identical pre- and postvideo case noticing assessment based on the example provided in the Framework section (see Figure 4) that focused on attending to and interpreting students’ spoken and written mathematical thinking and their technology engagement. Research has illustrated that PSMTs and practicing teachers often struggle with the skill of deciding how to respond (e.g., Dick, 2017; Jacobs et al., 2010), and the skill of deciding is even more complex for a task situated in a technology-mediated learning environment. Given this complexity, for this assessment we decided to focus only on the ways in which PSMTs attended and interpreted.
Data included the PSMTs written responses to the pre and post video case noticing assessment, which took place during the first and last weeks of the course. We collected eight responses on the preassessment and seven on the postassessment. The one PSMT who did not complete the postassessment was excluded from analysis.
The identical pre- and postassessment included the video clip of Eden and McKenzie (see Figure 3 for the transcript) and written prompts for the PSMTs to answer. Prior to completing the preassessment and in line with the design principles, PSMTs engaged with the Desmos activity as a learner to provide context for the video clip they would later examine. Following their engagement as learners, the PSMTs watched the video clip and responded to two noticing prompts. The first prompt focused on attending to the students’ spoken and written mathematical thinking and engagement with the technology. The second prompt focused on interpreting the students’ understanding of vertical asymptotes:
1. Describe how the students determined the location of the vertical asymptote for a rational function of the form
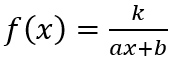
2. Interpret the students’ current understanding of vertical asymptotes. Provide evidence from the video to support your claims.
Analysis
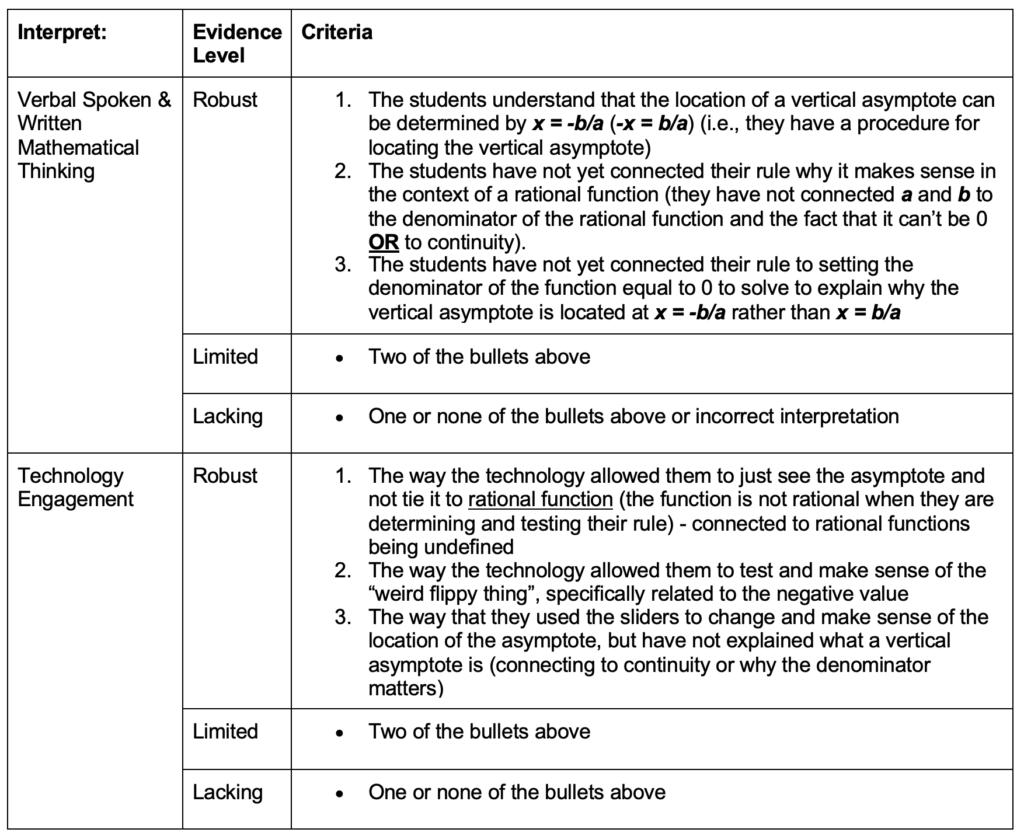
Data were analyzed using a coding rubric (see Figures 6 and 7) designed based on the NITE framework (see Figure 1). Similar to the coding scheme used by Jacobs et al. (2010), the rubric included three levels of evidence (i.e., lacking, limited, and robust) on each of the four components in the framework, robust being aligned with the example in Figure 4. Since research indicates that the skills of attending and interpreting are interwoven (e.g., Superfine et al., 2017), we coded PSMT responses across both prompts. In other words, if students attended in their interpret response, it was coded as attending, and vice versa.
Figure 6
Rubric for Attending to Students’ Spoken and Written Mathematical Thinking and Technology Engagement
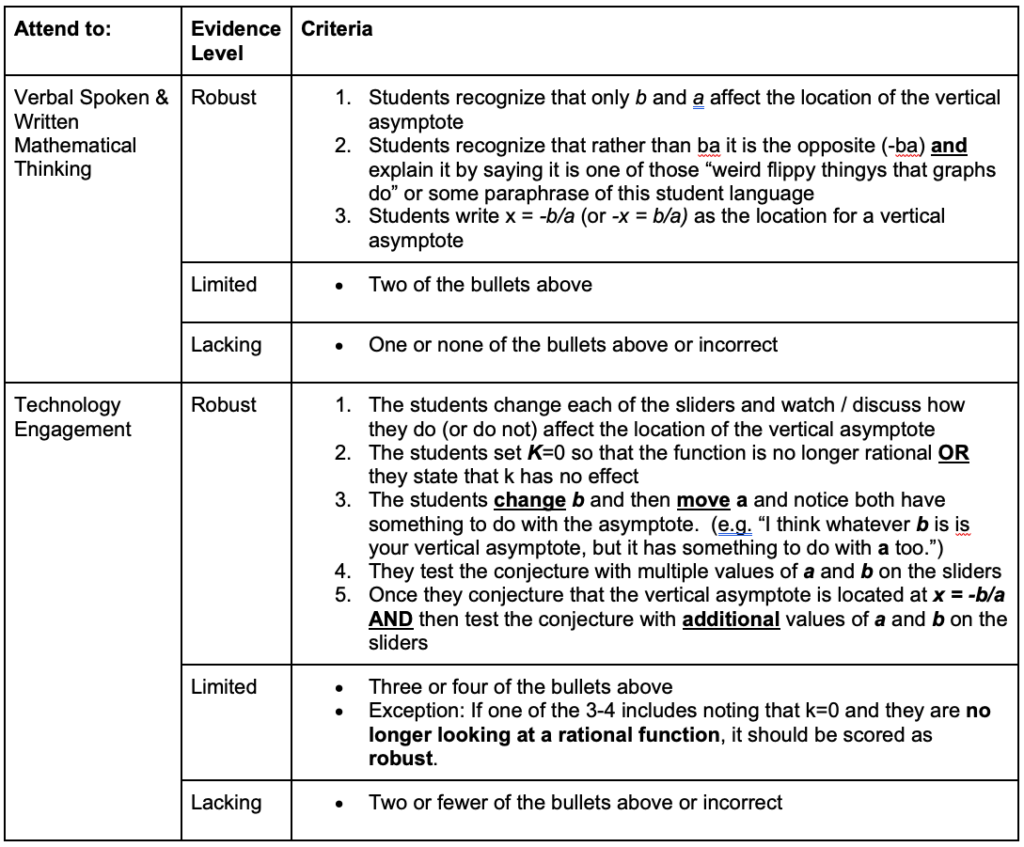
Figure 7
Rubric for Interpreting Students’ Spoken and Written Mathematical Thinking and Technology Engagement
We used an iterative process of refinement to achieve consistent application of the codes (as recommended in DeCuir-Gunby et al., 2011). We began by having the entire research team code a blinded PSMT response. All discrepancies were discussed until consensus was reached by the entire team. As needed, we refined the coding rubric to reflect the changes based on these conversations.
Using the final coding rubric (see Figures 6 and 7), each remaining blinded PSMT response was coded by two researchers, and all discrepancies were discussed by the entire team until reconciled. After coding was complete, tables were created to summarize the frequencies of each evidence level on the pre- and postassessments, as well as tables to capture the PSMTs’ change in evidence level from the pre- to postassessment. Finally, we created tables to describe the coordination of attending to students’ spoken and written mathematical thinking and technology engagement and the coordination of the interpretation of students’ spoken and written mathematical thinking and technology engagement, as seen in Figure 4.
Findings
On the preassessment, the PSMTs in this study collectively demonstrated higher levels of evidence for the attention to and interpretation of students’ spoken and written mathematical thinking than the attention to and interpretation of technology (see Table 1). With respect to the attention to spoken and written mathematical thinking, six PSMTs demonstrated at least limited evidence, and one demonstrated lacking evidence. Four PSMTs demonstrated at least limited evidence when interpreting the students’ spoken and written mathematical thinking, and three demonstrated lacking evidence. This result contrasts with three PSMTs and no PSMTs demonstrating at least limited evidence on the attention to and interpretation of technology engagement respectively.
Table 1
Summary of PSMTs’ Evidence Level on the Preassessment
| Evidence Level | Attend | Interpret | ||
|---|---|---|---|---|
| Spoken and Written Mathematical Thinking | Technology Engagement | Spoken and Written Mathematical Thinking | Technology Engagement | |
| Robust | 1 | 0 | 2 | 0 |
| Limited | 5 | 3 | 2 | 1 |
| Lacking | 1 | 4 | 3 | 6 |
On the postassessment, the PSMTs collectively demonstrated higher levels of evidence for the attention to students’ spoken and written mathematical thinking and attention to technology engagement (see Table 2). Similar to the preassessment, six PSMTs demonstrated at least limited evidence of attention to students’ spoken and written mathematical thinking, and one demonstrated lacking evidence. Notably, four of those PSMTs achieved robust evidence compared to only one on the preassessment.
Table 2
Summary of PSMTs’ Evidence Level on the Postassessment
| Evidence Level | Attend | Interpret | ||
|---|---|---|---|---|
| Spoken and Written Mathematical Thinking | Technology Engagement | Spoken and Written Mathematical Thinking | Technology Engagement | |
| Robust | 4 | 0 | 0 | 0 |
| Limited | 2 | 6 | 2 | 2 |
| Lacking | 1 | 1 | 5 | 5 |
Six PSMTs demonstrated limited evidence of attention to technology engagement, and one of the PSMTs demonstrated lacking evidence. On the preassessment, four PSMTs demonstrated at least limited evidence of the interpretation of students’ spoken and written mathematical thinking, whereas only two did on the postassessment. While no PSMTs demonstrated at least limited evidence of the interpretation of technology engagement on the preassessment, two did on the postassessment.
Through comparison of the rubric levels (i.e., lacking, limited, and robust evidence) of the pre- and postassessment, we documented level changes of PSMTs’ engagement with noticing students’ mathematical thinking in technology-mediated environments (see Table 3 for summary of results). The change in evidence levels revealed that PSMTs demonstrated the most growth in attending to students’ spoken and written mathematical thinking and attending to students’ technology engagement. We did not see parallel growth regarding the interpretation of students’ spoken and written mathematical thinking and the interpretation of students’ technology engagement. Looking across the PSMTs’ interpretation of spoken and written mathematical thinking, despite the stagnation or regression in evidence level from the pre- to postassessment, it is important to note that one PSMT demonstrated robust evidence for their interpret response on the preassessment, indicating that PSMTs may interpret the students’ mathematical thinking at a robust level.
Table 3
Summary of PSMTs’ Change in Coding Level From Pre- to Postassessment
| Change in Evidence Level From Pre-Post | Attend | Interpret | ||
|---|---|---|---|---|
| Spoken and Written Mathematical Thinking | Technology Engagement | Spoken and Written Mathematical Thinking | Technology Engagement | |
| Remained robust | 1 | 0 | 0 | 0 |
| Improvement in level | 3 | 3 | 0 | 1 |
| Same level | 2 | 4 | 3 | 6 |
| Decline in level | 1 | 0 | 4 | 0 |
With respect to interpreting the students’ technology engagement, none of the PSMTs demonstrated robust evidence. Thus, these findings show mixed results as to how explicitly sharing the NITE framework and providing opportunities for PSMT practice supported their engagement with the individual noticing skills of attending to and interpreting students’ mathematical thinking in technology-mediated environments. In our discussion, we will address potential reasons for these findings.
Since a teacher’s pedagogical response depends upon both attending to and interpreting students’ spoken and written mathematical thinking and students’ technology engagement, and how the two inform one another, in the sections that follow, we discuss the findings according to changes in the PSMTs’ coordination between students’ spoken and written mathematical thinking and technology engagement. We define coordination as having PSMTs demonstrate at least limited evidence on both attention to (or interpretation of) students’ spoken and written mathematical thinking and the attention to (or interpretation of) technology engagement. Full coordination occurs when PSMTs demonstrate robust attention to and robust interpretation of both students’ spoken and written mathematical thinking and technology engagement. This level of coordination is the goal because it depicts the students’ current understanding using all information available.
Coordination of Attending
Regarding PSMTs’ coordination between the attention to students’ spoken and written mathematical thinking and the attention to technology engagement, the PSMTs collectively demonstrated growth. Figure 8 demonstrates that only two PSMTs demonstrated coordination on the preassessment (denoted in green on Figure 8); whereas, on the postassessment, five PSMTs demonstrated coordination. Two examples demonstrate where PSMTs went from no coordination on the preassessment to coordination on the postassessment. While these are both considered improvements, each includes a typical example of no coordination.
Figure 8
Comparison of PSMTs’ Coordination of Attend on the Pre- and Postassessment
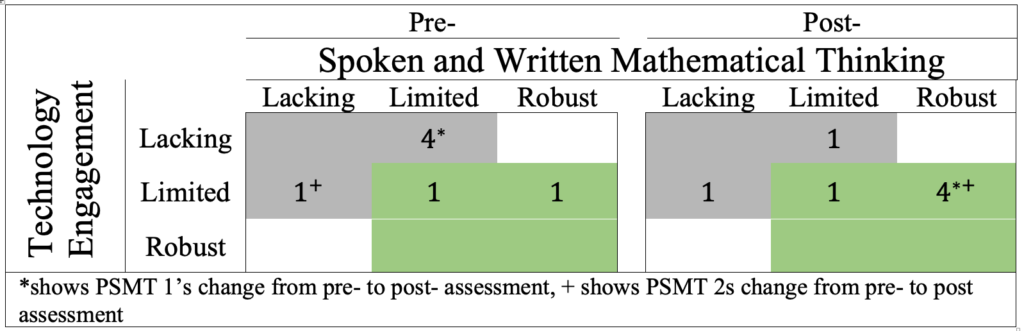
PSMT 1’s responses are an example of the improvement from no coordination on the preassessment (denoted in gray with an * on Figure 8) to coordination on the postassessment (denoted in green with an *; see also Table 4). On the preassessment PSMT 1 demonstrated lacking evidence of attention to students’ spoken and written mathematical thinking and limited evidence of attention to technology engagement. PSMT 1 did identify that the students arrived at a formula, but incorrectly identified the formula as negative a divided by b instead of negative b divided by a. Furthermore, PSMT 1 did not explicitly discuss how the students determined that only a and b affect the location of the asymptote, nor did they discuss the language used by the students.
PSMT 1 did attend to four of the details for technology engagement. They noted that the students moved the sliders, that they began with slider b and then made changes to slider a, and that the students changed parameter k to 0 (therefore, implicitly indicating that k had no effect), and that the students tried different values for the parameters (i.e., “setting a to 0 and moved b and then set a to 0 and moved b”) to formulate an initial conjecture. However, because PSMT 1 made no explicit connections to the ways the technology helped the students make particular discoveries, there is no evidence of coordination. This conclusion can be drawn from PSMT 1’s vague language: “By doing that they finally figured out that a and b are closely related.”
Table 4
Quotations From PSMT 1’s Pre- and Postassessment
| Pre | Post |
|---|---|
| They started by setting a to 0 and moved and then set to 0 and moved a. By doing that they finally figured out that and are closely related when figuring out the vertical asymptote. … Eventually they realized that to find the vertical asymptote they got the equation of a/b and switch the sign… They left equal to 0 and would only change and within the problem to see that those variables are closely related to the vertical asymptotes. | They first began by moving all three sliders until they realized that when they move ‘a’ slider to 0, the graph becomes a straight line. Then they began to move slider ‘b’ in which they determined that it causes the graph to move up and down. Then they set ‘k’ to 0 and moved both ‘a’ and ‘b’ to determine that the asymptote moves when sliding the slider negatively and positively. By moving the sliders ‘a’ and ‘b’ they came to realize that ‘a’ is half of ‘b’ and that determines the location of the vertical asymptote. They determined that the vertical asymptote is the variable ‘b’ divided by the variable ‘a’… Then they came to the conclusion that the sign in front of the vertical asymptote is opposite sign of the division when they mention that they think “it’s one of those flippy thingys”. The students current understanding of vertical asymptotes is that it is variable ‘b’ divided by variable ‘a’ and the sign flipped. |
On the postassessment, PSMT 1 correctly attended to all three details of the students’ mathematical thinking (robust evidence) by identifying the formula that the students produced, taking note of the students’ language, and addressing that only a and b affect the location of the asymptote. PSMT 1 attended to the same four details of technology engagement as they did on the preassessment. However, most notably PSMT 1 demonstrated coordination on the postassessment. PSMT 1 explicitly discussed how the students’ manipulation of the sliders helped them determine which parameters determined the location of the vertical asymptote.
Another example of the ways in which PSMTs improved in their noticing was PSMT 2, who also improved from no coordination on the preassessment (denoted in gray with a + on Figure 8) to coordination on the postassessment (denoted in green with a +). However, unlike the previous example, PSMT 2 demonstrated limited evidence of attention to students’ spoken and written mathematical thinking and lacking evidence of attention to technology engagement, on the preassessment (see Table 5). PSMT 2 correctly noted that the students determined a procedure for finding the location of the vertical asymptote which only incorporated parameters a and b. Regarding technology engagement, they did mention that the students “figured out that it was not impacted by k” but did not explicitly connect this to the students’ technology engagement. PSMT 2 did not take note of when or how the students used the technology to refine their understanding of which variables affect the location of the asymptote nor did they comment on how the students tested their conjectures using the technology.
Table 5
Quotations From PSMT 2’s Pre- and Postassessment
| Pre | Post |
|---|---|
| They first figured out that it was not impacted by …They knew from the graph that both and changed the vertical asymptote, it was just determining how they were connected. They figured out that it was and then changing the sign which is the equivalent to setting it equal to zero and solving the equation, they just didn’t know to solve the equation that way. | At first the students didn’t think you could determine the asymptote with those numbers alone, and also thought and did the same thing, while moving all the sliders. When moving the sliders, they said that didn’t move the vertical asymptote, but and did. Then moving only and sliders, one student said she thought it could be because it wasn’t exactly or . Then, the other student noticed that which was was and the vertical asymptote was at . So, they determined it was by trying it multiple times with different numbers but giving it a negative which they referred to as “one of those weird flippy thingy’s” “I would tell my friend to divide ”. |
Again, we saw a stark contrast on PSMT 2’s postassessment, in which they demonstrated coordination with robust evidence of attention to students’ spoken and written mathematical thinking and limited evidence of attention to technology engagement. PSMT 2 attended to all three details of the students’ spoken and written mathematical thinking. PSMT 2 also explicitly noted how and when the students manipulated the sliders. Coordination between attention to the students’ spoken and written mathematical thinking and attention to technology engagement was evident throughout their response. For example, PSMT 2 made the connection between what the students did with the technology (e.g., tested multiple values) to arrive at and ultimately refine their conjectures about the location of the vertical asymptote (e.g., revised b/a to the opposite of b/a).
Coordination of Interpreting
The findings regarding the PSMTs’ coordination between the interpretation of students’ spoken and written mathematical thinking and the interpretation of technology engagement did not demonstrate parallel growth to the coordination of attending (see Figure 9). The majority of PSMTs did not demonstrate coordination. In fact, none of the PSMTs demonstrated coordination on the postassessment. PSMT 3’s responses (denoted on Figure 9 with a ~) are a typical example of no coordination between the interpretation of students’ spoken and written mathematical thinking and the interpretation of technology engagement. PSMT 3 demonstrated limited evidence of the interpretation of students’ spoken and written mathematical thinking and lacking evidence of the interpretation of technology engagement on the preassessment (see Table 6). PSMT 3 indicated that the students understood that the location of a vertical asymptote can be determined by “b/a, then flip the sign.”
Figure 9
Comparison of PSMTs’ Coordination of Interpret on the Pre- and Postassessment
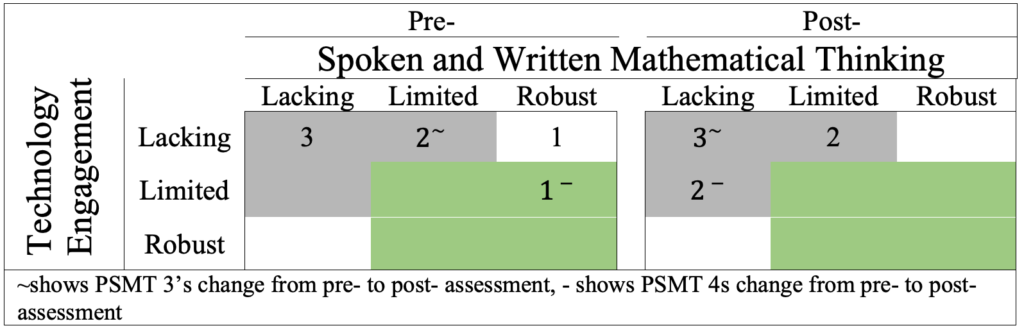
Table 6
Quotations from PSMT 3’s Pre- and Postassessment
| Pre | Post |
|---|---|
| The students used trial and error until they noticed a pattern, then tested any patterns they found. They landed on b/a, then flip the sign. This is the correct method for finding the asymptote, as it is equivalent to solving the equation ax+b=0. The students used trial and error to see which parameter would affect the asymptote. The students determined that k did not affect the location of the asymptote, and focused on a and b. Their formula for the vertical asymptote is correct, though it seemed their understanding of why was lacking. The two used terms like “flippy thingy” which seemed two show a lack of understanding why the ratio defining the asymptote had the opposite sign of what they expected. | The students used trial and error to see which parameter would affect the asymptote. The students determined that k did not affect the location of the asymptote, and focused on a and b… By the end of the activity, students determined the correct equation for the vertical asymptote, x = -ba. This was shown when they determined and stated that the asymptote was -x = ba, which is equivalent. |
PSMT 3 also explained that while the students arrived at the correct formula there was no evidence that they made the connection to setting the denominator equal to 0 to figure out why there was an opposite sign in their formula. While PSMT 3 noted that the students used the technology in specific ways, such as using trial and error to test their conjectures, PSMT 3 did not explicitly indicate how the technology was used nor did they interpret how these actions informed their understanding, which shows a lack of coordination.
On the postassessment, PSMT 3 again noted that the student understood the procedure for the location of the vertical asymptote. However, this time PSMT 3 did not mention the lack of evidence for a connection to the denominator of the rational function. Similar to the preassessment, because PSMT 3 did not interpret how the students’ technology use informed their understanding of the location of the vertical asymptote, there is no evidence of coordination. PSMT 3’s list-like structure of what the students did with the technology is common to PSMTs who did not demonstrate coordination between the interpretation of students’ spoken and written mathematical thinking and the interpretation of technology engagement. Such PSMTs treated the technology as separate facts documenting what the students did during the investigation instead of using those facts as evidence for what the students understood.
While we feel disheartened that none of the PSMTs demonstrated coordination of interpreting on the postassessment, PSMT 4 did demonstrate coordination on the preassessment, with robust evidence of interpreting students’ spoken and written mathematical thinking and limited evidence of interpreting technology engagement (denoted on Figure 9 with a –). PSMT 4 demonstrated coordination in balancing their interpretations of the students’ spoken and written mathematical thinking with the interpretations of their technology engagement (see Table 7).
For example, PSMT 4 discussed how the students’ engagement with the technology enabled them to make sense of the “weird flippy thingy.” They also noted that the students understood there is a procedure for finding the location of the vertical asymptote but the students had not yet connected their procedure to setting the denominator equal to 0 and solving. Additionally, PSMT 4 noted that the students used the sliders to make sense of the location of the vertical asymptote (i.e., arrive at a procedure) but that the students did not explain what a vertical asymptote is (i.e., did not realize that the location is where the function in undefined).
This response starkly contrasted with PSMT 4’s postassessment response. Similar to PSMT 3 and other PSMTs that did not demonstrate coordination, PSMT 4 listed what the students did with technology but did not interpret what these actions meant for the students’ understanding of the location of the vertical asymptote.
Table 7
Quotations From PSMT 4’s Pre- and Postassessment
| Pre | Post |
|---|---|
| As Eden and McKenzie changed the values on the simulator, they quickly eliminated k as a significant factor. As they continued to manipulate a and b, they realized those two values were key to where the vertical asymptote fell. By noticing how changes in a and b affected the graph, they found the solution, which was the negative of b divided by a. They then tested their solution by inputting different values for a and b, which confirmed their hypothesis. Eden and McKenzie had no real understanding that the vertical asymptote represents where a function is undefined; they are just looking for a connection between a, b, and the x-value of the vertical asymptote. The student who first discovered the solution even states that she thinks having to change the sign is “one of those weird flippy thingies that doesn’t really make sense in math.” If they had been setting the denominator equal to zero, they would have clearly understood why the sign was reversed. | The students moved the sliders back and forth to see what changes were made in the graph. They did not appear to be looking at the equation at the top of the screen. They moved b first and then they started moving a. They say that a and b do the same thing. They discovered that when a is 0, the function becomes a horizontal line that changes with b. They know that k doesn’t affect the vertical asymptote. |
Discussion
Findings from this study suggest that using the NITE framework did support PSMTs’ noticing of students’ mathematical thinking within a technology-mediated environment, which is consistent with Thomas et al.’s (2015) findings in nontechnological environments. For example, results show that PSMTs developed the skill of attending to technology engagement in coordination with students’ spoken and written mathematical thinking, and the NITE framework appears to have supported them in their engagement with this work. However, it did not seem to support PSMTs on all components of the framework in the same way.
Parallel growth was not evidenced in the PSMTs’ skill of interpreting technology engagement in coordination with the students’ spoken and written mathematical thinking. Our findings are consistent with the literature indicating that interpreting students’ mathematical thinking is a difficult practice (e.g., Stahnke et al.’s, 2016, synthesis of noticing literature) as PSMTs’ interpretations are dependent upon attending as the skills are interwoven (e.g., Superfine et al., 2017). These findings suggest that the skill of interpreting in a technology-mediated environment is even more challenging than when technology is not involved.
While we cannot fully explain the lack of growth related to PSMTs’ interpretations, we propose a few potential reasons for this result. Possibly, the PSMTs’ content knowledge of rational functions influenced their interpretations, which would be consistent with prior research connecting noticing to content knowledge (e.g., Dick, 2017; Dreher & Kuntze, 2015; Sánchez-Matamoros et al., 2015). While the PSMTs all had extensive prior experiences with rational functions, rational functions were not explicitly discussed in this course. As a result, the PSMTs’ interpretations of this video example are possibly not representative of their skills as a whole.
Another possible interpretation is related to PSMTs’ visions of high-quality mathematics instruction, which also influences the practice of noticing (e.g., Sherin, 2014; Sherin et al., 2008). If PSMTs hold the belief that teaching should focus on imparting procedural knowledge, it follows that those PSMTs would focus on the students’ success in finding a rule for locating the vertical asymptote, instead of focusing on how the students were or were not grappling with the conceptual connections between the rule and the structure of rational functions.
This first semester of the COVID-19 pandemic undoubtedly influenced the PSMTs. Multiple PSMTs had limited or robust interpretations of the students’ written and spoken work in the preassessment that regressed in the postassessment. As the skill of interpreting demands a heavier cognitive load than attending, it is possible that the PSMTs’ emotional loads from the pandemic (e.g., stress and anxiety or change in modality) interfered with their available cognitive load to interpret to the best of their ability. Specifically, the PSMTs’ responses on the postassessment were less detailed than on the preassessment.
Last and importantly, the PSMTs were possibly expending more mental effort on integrating what they learned by focusing on the foundational skill of attending to students’ spoken and mathematical thinking, attending to students’ technology engagement, and coordinating between the two. In our study, the PSMTs demonstrated higher levels of evidence with respect to attend than interpret, implying that the skill of attending develops prior to interpretation. Research supports this hypothesis, as Jacobs et al. (2010) indicated that attending to students’ mathematical thinking is “a foundational skill for interpreting and deciding how to respond” (p. 195). Thus, with continued practice the PSMTs may improve the level of evidence for interpreting students’ spoken and mathematical thinking and interpreting students’ technology engagement after they have developed the foundational skill of attending.
Implications for Mathematics Teacher Educators
Findings from this study suggest that mathematics teacher educators should provide PSMTs with more opportunities to engage with examples of students working in technology-mediated learning environments. PSMTs’ early experiences may benefit from careful scaffolding using the language of the NITE framework. As a result, we have refined our introductory module to include an explicit example of what robust attention to and interpretation of students’ written or spoken responses and of students’ technology engagement entails, and we have added questions that prompt the PSMTs to consider the relationship between technology engagement and mathematical thinking. In addition, we have included questions that require PSMTs to consider how interpreting students’ mathematical thinking is dependent upon the ability to attend and how these skills are interwoven (e.g., Superfine et al., 2017).
We suggest that mathematics teacher educators who are working to design such experiences for their PSMTs include these types of explicit scaffolds when PSMTs are engaged in noticing students’ thinking in technology-mediated learning environments. Additionally, mathematics teacher educators should work to incorporate a variety of opportunities for PSMTs to practice the pedagogical intricacies associated with teacher noticing in such environments.
Noticing students’ mathematical thinking in a technology-mediated environment is a complex but incredibly important practice for preservice teachers to develop. The results of this study suggest that using the NITE framework to support PSMTs’ development of this practice has promise, especially related to coordinating students’ attention to written and spoken mathematical thinking with their technology engagement. With further refinements to the project modules based on the findings of this study, we hope to see similar results related to PSMTs’ interpretations.
Author Note
This project is supported by the National Science Foundation under Grant DUE 1820998 awarded to Middle Tennessee State University, Grant DUE 1821055 awarded to University of North Carolina at Charlotte, Grant DUE 1820967 awarded to East Carolina University, and DUE 1820976 awarded to NC State University. Any opinions, findings, and conclusions or recommendations expressed herein are those of the principal investigators and do not necessarily reflect the views of the National Science Foundation.
Reference
Amador, J.M., Bragelman, J., & Superfine, A.C. (2021). Prospective teachers’ noticing: A literature review of methodological approaches to support and analyze noticing. Teaching and Teacher Education, 99, 1-16. https://doi.org/10.1016/j.tate.2020.103256
Arzarello, F., Olivero, F., Paola, D., & Robutti, O. (2002). A cognitive analysis of dragging practices in Cabri environments. ZDM, 34(2), 66–72. https://doi.org/10.1007/BF02655708
Association of Mathematics Teacher Educators. (2017). Standards for preparing teachers of mathematics. https://amte.net/standards
Baccaglini-Frank, A., & Mariotti, M. A. (2010). Generating conjectures in dynamic geometry: The maintaining dragging tool. International Journal of Computers in Mathematics Learning, 15(3), 225–253. https://doi.org/10.1007/s10758-010-9169-3
Bailey, N. G., Yalman Ozen, D., McCulloch, A. W., Dick, L., Lovett, J. N., & Cayton, C. (2021). AMTE’s 2021 NTLI Fellowship: Using a framework to teach preservice mathematics teachers how to professionally notice within technology-mediated learning environments. In E. Langran & L. Archambault (Eds.), Proceedings of the 32nd annual conference of the Society for Information Technology and Teacher Education (pp. 1359–1368). Association for the Advancement of Computing in Education. https://www.learntechlib.org/primary/p/219385/
Chandler, K. (2017). Examining how prospective secondary mathematics teachers notice students’ thinking on a paper and pencil task and a technological task [Unpublished doctoral dissertation]. NC State University, Raleigh, NC, United States.
Clements, D. (2007). Curriculum research: Toward a framework for “Research-Based Curricula.” Journal for Research in Mathematics Education, 38(1), 35–70.
Cobb, P., Confrey, J., diSessa, A., Lehrer, R., & Schauble, L. (2003). Design experiments in educational research. Educational Researcher, 32(1), 9–13. https://doi.org/10.3102/0013189X032001009
DeCuir-Gunby, J. T., Marshall, P. L., & McCulloch, A. W. (2011). Developing and using a codebook for the analysis of interview data: An example from a professional development research project. Field Methods, 23(2), 136–155. https://doi.org/10.1177/1525822X10388468
Dick, L. K. (2017). Investigating the relationship between professional noticing and specialized content knowledge. In E. O. Schack, M. H. Fisher, & J. A. Wilhelm (Eds.), Teacher noticing: Bridging and broadening perspectives, contexts, and frameworks (pp. 339–358). Springer, Cham. https://doi.org/10.1007/978-3-319-46753-5
Dick, L. K., McCulloch, A. W., & Lovett, J. N. (2021). When students use technology tools, what are you noticing? Mathematics Teacher: Learning and Teaching PK-12, 114(4), 272–283. https://doi.org/10.5951/MTLT2020.0285
Dick, T., & Hollebrands, K. (2011). Focus on high school mathematics: Reasoning and sense making with technology. National Council of Teachers of Mathematics.
Dreher, A., & Kuntze, S. (2015). Teachers’ professional knowledge and noticing: The case of multiple representations in the mathematics classroom. Educational Studies in Mathematics, 88(1), 89–114. https://doi.org/10.1007/s10649-014-9577-8
Fischer, M. H., Thomas, J., Jong, C., Schack, E. O., & Dueber, D. (2019). Comparing preservice teachers’ professional noticing skills in elementary mathematics classrooms. School Science and Mathematics, 119, 142–149. https://doi.org/10.1111/ssm.12324
Grossman, P., Compton, C., Igra, D., Ronfeldt, M., Shanhan, E., & Williamson, P. (2009). Teaching practice: A cross-professional perspective. Teachers College Record, 111(9), 2055–2100.
Ivars, P., Fernández, C., & Llinares, S. (2020). A learning trajectory as a scaffold for pre-service teachers’ noticing of students’ mathematical understanding. International Journal of Science and Mathematics Education, 18, 529–548.
Jacobs, V. R., Lamb, L. L., & Philipp, R. A. (2010). Professional noticing of children’s mathematical thinking. Journal for Research in Mathematics Education, 41(2), 169–202. https://doi.org/10.5951/jresematheduc.41.2.0169
Jacobs, V. R., & Spangler, D. A. (2017). Research on core practices in K-12 mathematics teaching. In J. Cai (Ed.), Compendium for research in mathematics education (pp. 766–792). National Council of Teachers of Mathematics.
Jong, C., Schack, E. O., Fisher, M. H., Thomas, J., & Dueber, D. (2021). What role does professional noticing play? Examining connections with affect and mathematical knowledge for teaching among preservice teachers. ZDM, 53(1), 151–164.
Krupa, E. E., Huey, M., Lesseig, K., Casey, S., & Monson, D. (2017). Investigating secondary preservice teacher noticing of students’ mathematical thinking. In E. O. Schack, M. H. Fisher, & J. A. Wilhelm (Eds.), Teacher noticing: Bridging and broadening perspectives, contexts, and frameworks (pp. 49–72). Springer, Cham. https://doi.org/10.1007/978-3-319-46753-5_4
Leatham, K. R., Peterson, B. E., Stockero, S. L., & van Zoest, L. R. (2015). Conceptualizing mathematically significant pedagogical opportunities to build on student thinking. Journal for Research in Mathematics Education, 46(1), 88–124.
Lovett, J. N., Dick, L. K., McCulloch, A. W., Sherman, M. F., & Martin, K. (2019). Preservice mathematics teachers’ professional noticing of students’ mathematical thinking with technology. Journal of Computers in Mathematics and Science Teaching, 38(4), 305–319. https://www.learntechlib.org/primary/p/183521/
Lovett, J. N., McCulloch, A. W., Dick, L. K., & Cayton, C. (2020). Design principles for examining student practices in a technology-mediated environment. Mathematics Teacher Educator, 8(3), 120–133. https://doi.org/10.5951/MTE.2020.0007
Mason, J. (2002). Researching your own practice: The discipline of noticing. Routledge.
Mitchell, R. N., & Marin, K. A. (2015). Examining the use of a structured analysis framework to support prospective teacher noticing. Journal of Mathematics Teacher Education, 18(6), 551–575. https://doi.org/10.1007/s10857-014-9294-3
Moreno, M., Sánchez-Matamoros, G., Callejo, M.L., Perez-Tyteca, P., & Llinares, S. (2021). How prospective kindergarten teachers develop their noticing skills: The instrumentation of a learning trajectory. ZDM, 53, 57–72. https://doi.org/10.1007/s11858-021-01234-5
Nagle, C., Casey, S., & Carney, M. (2020). Professional noticing on a statistical task. Investigations in Mathematics Learning, 12(1), 10–27. https://doi.org/10.1080/19477503.2018.1534539
National Center for Education Statistics. (2020). Characteristics of public school teachers. https://nces.ed.gov/programs/coe/indicator_clr.asp
Philipp, R., Jacobs, V. R., & Sherin, M. G. (2014). Noticing of mathematics teachers. In S. Lerman (Ed), Encyclopedia of mathematics education (pp. 465–466). https://doi.org/10.1007/978-94-007-4978-8_120
Sánchez-Matamoros, G., Fernandez, C., & Llinares, S. (2015). Developing pre-service teachers’ noticing of students’ understanding of the derivative concept. International Journal of Science and Mathematics Education, 13, 1305–1329. https://doi.org/10.1007/s10763-014-9544-y
Santagata, R. & Yeh, C. (2016). The role of perception, interpretation, and decision making in the development of beginning teachers’ competence. ZDM, 48(1–2), 153–165. http://doi.org/10.1007/s11858-015-0737-9
Schack, E. O., Fisher, M. H., Thomas, J. N., Eisenhardt, S., Tassell, J., & Yoder, M. (2013). Prospective elementary school teachers’ professional noticing of children’s early numeracy. Journal of Mathematics Teacher Education, 16(5), 379–397. https://doi.org/10.1007/s10857-013-9240-9
Sherin, M. G. (2014). The development of teachers’ professional vision in video clubs. In R. Goldman, R. Pea, B. Barron, & S. Derry (Eds.), Video research in the learning sciences, (pp. 383–395). Routledge.
Sherin, M. G., Russ, R. S., Sherin, B. L., & Colestock, A. (2008). Professional vision in action: An exploratory study. Issues in Teacher Education, 17(2), 27–46.
Smith, M. S., & Stein, M. (2018). Five practices for orchestrating productive mathematics discussions. National Council of Teachers of Mathematics.
Stahnke, R., Schueler, S., & Roesken-Winter, B. (2016). Teachers’ perception, interpretation, and decision-making: A systematic review of empirical mathematics education research. ZDM, 48(1–2), 1–27. https://doi.org/10.1007/s11858-016-0775-y
Stockero, S. L. (2020). Transferability of teacher noticing. ZDM, 53, 73–84. https://doi.org/10.1007/s11858-020-01198-y
Stockero, S.L., & Van Zoest, L.R. (2013). Characterizing pivotal teaching moments in beginning mathematics teachers’ practice. Journal of Mathematics Teacher Education, 16, 125–147. https://doi.org/10.1007/s10857-012-9222-3
Superfine, A. C., Fisher, A., Bragelman, J., & Amador, J. M. (2017). Shifting perspectives on preservice teachers’ noticing of children’s mathematical thinking. In E. O. Schack, M. H. Fisher, & J. A. Wilhelm (Eds.), Teacher noticing: Bridging and broadening perspectives, contexts, and frameworks (pp. 409–420). Springer, Cham. https://doi.org/10.1007/978-3-319-46753-5_24
Thomas, J. N., Eisenhardt, S., Fisher, M. H., Schack, E. O., & Tassell, J. (2015). Professional noticing: Developing responsive mathematics teaching. Teaching Children Mathematics, 21(5), 294–303. https://doi.org/10.5951/teacchilmath.21.5.0294
Teuscher, D., Leatham, K.R., & Peterson, B.E. (2017). From a framework to a lens: Learning to notice student mathematical thinking. In E. O. Schack, M. H. Fisher, & J. A. Wilhelm (Eds). Teacher noticing: Bridging and broadening perspectives, contexts, and frameworks (pp. 31–48). Springer, Cham. https://doi.org/10.1007/978-3-319-46753-5_3
Trouche, L., & Drijvers, P. (2010). Handheld technology for mathematics education: Flashback into the future. ZDM, 42(7), 667–681. https://doi.org/10.1007/s11858-010-0269-2
Walkoe, J., Wilkerson, M., & Elby, A. (2017). Technology-mediated teacher noticing: A goal for classroom practice, tool design, and professional development. In B. K. Smith, M. A. Borge, E. Mercier, & K. Y. Lim (Eds.), 12th international conference on computer supported collaborative learning conference proceedings (Vol. 1, pp. 65–70). International Society of the Learning Sciences.
Wilson, P. H., Lee, H. S., & Hollebrands, K. F. (2011). Understanding prospective mathematics teachers’ processes for making sense of students’ work with technology. Journal for Research in Mathematics Education, 42(1), 39–64. https://doi.org/10.5951/jresematheduc.42.1.0039
Yeo, S., & Webel, C. (2019). Preservice teachers’ use of noticing practices to evaluate technological resources. In S. Otten, A. Candela, Z. de Araujo, C. Haines, & C. Munter (Eds.), Proceedings of the 41st annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Issue 41, pp. 1048–1056). University of Missouri.
Appendix
Transcript of Eden and McKenzie Working on the Vertical Asymptote Desmos Activity
| Transcript | |
|---|---|
| McKenzie: | The asymptote isn't based on... just those numbers alone. Because look, if you do it there... it's not going to be exactly on that number. [Student drags slider b to change the value from 5 to 4 which moves the graph to the right on the x axis.] |
| Eden: | Yeah… |
| McKenzie: | So… how can you predict the location of a vertical asymptote given the function rule? I think... wait… I don't know… I'm confused because 'a' and 'b' do the same thing… wait move 'a' [Student drags slider a to change the value from 5 to 2 which results the graph moving to the left 3 places and the graph stretches horizontally.] |
| McKenzie: | I feel like it makes it bigger, or is that just me? |
| Eden: | Oh oops! What did I just do? |
| McKenzie: | Go to zero. [Student drags slider to change the value to 0 which results in a horizontal line at y=1.] |
| Eden: | But it's still three. |
| McKenzie: | Go to zero for 'b'. [Student drags slider b to change the value to 0 which results in the function no longer appearing in the graphing window; the asymptote is still visible.] |
| McKenzie: | That moves up and down because… this doesn't move vertical asymptote. [Student drags slider k to change the value from 1 to 12 which does not affect the vertical asymptote but results in the graph stretching vertically.] |
| McKenzie: | This moves your vertical asymptote, so something with that and this one is your vertical asymptote. [Student drags slider a to test values from -1 to 4 which results in the horizontal asymptote moving from left to right.] |
| McKenzie: | So I think that whatever 'b' is your vertical asymptote. |
| Eden: | I think it's... |
| McKenzie: | But it has something to do with 'a' too, though. |
| Eden: | I think it's… I think it's… um… [groaning] divided by 'a'. Yeah, I think it's, I think it's 'b' divided by 'a' cause, cause look two divided by four is what? |
| McKenzie: | Two divided by four is one half but two divided by negative four is negative one half. |
| Eden: | I know, I think it's just, I think it's just one of those weird flippy thingy with that graphs do. |
| McKenzie: | Let's try this number and… oh and I need to go down to this number. Hold on one… point five. [Student drags the sliders and sets the values at k = 0, a = -10, b = 5. K = 0 results in the graph not moving even when the student changes the a value from -10 to 0.] |
| McKenzie: | Oh! You’re right cause that's point five. |
| Eden: | I think it's one of those weird flippy thingy. That doesn't really make sense and yeah |
| McKenzie: | Or... This [laughing] or... |
| Eden: | Two… two and a four |
| McKenzie: | We can do two in here and four. [Student drags sliders a and b and sets the value of a to 2 and the value of b to 8 which changes the vertical asymptote from x=-.5 to x=-4] |
| Eden: | Yeah |
| McKenzie: | Yeah, it's one of those flip things. And then that's... |
| Eden: | So… if I were to define the vert... I would tell my friend to… divide... 'b', whatever 'b' is, by 'a' and then make it equals… okay, 'b' divided by 'a'. |
| McKenzie: | One sec, I have to write this out. |
| Eden: | Equals negative 'x' or whatever. |
| McKenzie: | Okay. |
![]()