Frameworks can influence the work of mathematics teacher educators (MTEs) in many different ways. Frameworks can suggest a structure around which MTEs design instruction, provide a common language for communicating with prospective teachers, and support prospective teachers as they design their own instruction. The Association of Mathematics Teacher Educators (AMTE, 2017) Standards for Preparing Teachers of Mathematics (SPTM) articulated the importance of frameworks in mathematics teacher education in indicator P.3.4, stating that
an effective mathematics teacher preparation program ensures that practice-based experiences, including mathematics methods courses and equivalent learning experiences, provide candidates with experiences using tools and frameworks grounded in research to develop core pedagogical practices and pedagogical content knowledge for teaching mathematics. (p. 35)
The document went on to explain that frameworks serve as “important vehicles for connecting theory and practice and guiding candidates in their work with authentic artifacts of teaching” (p. 36). Frameworks are thus positioned as important to the work of MTEs.
The field of mathematics teacher education has begun to consider seriously the ways and the extent to which MTEs follow such recommendations – how MTEs use research-based frameworks to build and explore our work with prospective mathematics teachers (PSMTs; e.g., see Kastberg et al., 2012, Kastberg et al, 2017). In 2005 Mewborn emphasized this work when she challenged the field to develop conceptual definitions for big ideas and frameworks for “long-used ideas” (p. 7) in mathematics teacher education.
With the articulation of new frameworks, however, comes the need to compare and contrast them to identify gaps and overlap, and the need to reconcile differences between those that rival each other (Lester, 2005). In doing so, the field need not coalesce around a single framework, but rather can adopt and adapt those that meet our goals (Lester, 2005).
If MTEs aim to meet the goals set forth by the AMTE SPTM, specifically as they relate to teaching mathematics with technology (C.1.6), the time is ripe for this careful consideration of the frameworks that have emerged related to teaching with technology. This paper describes our findings related to the frameworks that MTEs are currently using in their work of preparing secondary mathematics teachers to teach with technology.
Framing Our View of Frameworks
We adopted a broad view of frameworks for this work and speak of these frameworks in terms of what is being framed. Many phenomena are related to the pedagogy of learning to teach mathematics with technology that could be framed (i.e., viewed in a particular way). One might seek to frame the work of the MTE, the work of the mathematics teacher, or the work of the mathematics students. One might seek to frame technology itself.
Regardless of its object, framing takes an explicit theoretical stance regarding ways of viewing this object – how one might distinguish this phenomenon from other phenomena, how one might discern critical characteristics, and nuances of the phenomenon. Noting the importance of such work, Leatham (2019) stated, “We frame our work theoretically by drawing on, adapting, and developing theories (plausible explanations for phenomena) in order to delineate the scope and nature of the phenomena we study” (p. 169).
With this conceptualization of framing in mind, in this study we sought to answer the following research questions:
- What frameworks are MTEs using to frame their work related to teaching secondary mathematics teachers to teach with technology?
- What phenomena related to teaching mathematics with technology are these frameworks framing?
After the results of this study is a discussion of the findings. This discussion includes an examination of the sufficiency of these frameworks for helping frame these phenomena and questioning whether important phenomena might be related to learning to teach mathematics with technology that yet lack sufficient framing.
Methods
A set of frameworks identified by MTEs were the impetus for this study. These frameworks were elicited from a nationwide survey study focused on describing how secondary mathematics teacher preparation programs are preparing teachers to teach mathematics with technology. Primary sources for the frameworks elicited from the survey became the data sources for the current study (see Figure 1). Using qualitative methods these data were analyzed with respect to the research questions. Our specific data collection and analysis processes are described in detail in the sections that follow.
Figure 1 Methods for Data Collection

The Survey
Our survey was designed to elicit descriptive information about courses designed to address learning to teach mathematics with technology. Items targeted the structure of the course or courses, course learning objectives, different types of technology utilized and frequency of use, and types of learning activities (for a full report of this study see McCulloch et al., 2021). One survey item asked participants to “list any frameworks related to teaching mathematics with technology that are explicitly shared with PSMTs in their course(s).” Responses to this item are the focus of this paper.
Since our goal was to describe how teachers are being preparing to teach mathematics with technology widely, we aimed to reach all 4-year-university-affiliated secondary mathematics teacher preparation programs. To do so, we identified all accredited university secondary mathematics teacher preparation programs by visiting the department of public instruction websites for all 50 states. (We define secondary mathematics teacher preparation programs as programs that prepare PSTs to teach Grades 9-12. In some states designation includes some or all of Grades 6-8.)
We then verified that each university on the list had an undergraduate secondary mathematics teacher preparation program and identified an appropriate contact person. This search resulted in a list of 956 accredited programs. Using a presurvey email we confirmed the correct contact for 383 of the 956 (40%) accredited programs prior to survey distribution. The survey was sent to all 956 universities along with at least one reminder email if necessary, resulting in two to five email contacts per program.
The response rate was 30% overall, and 61% from those programs for which an appropriate contact had been confirmed. The overall response rate is larger than that of previous studies focused on this topic (Kersaint et al., 2003; Leatham, 2006), and the respondents represent a broad cross-section of universities from 48 of the 50 states and from different Carnegie classifications.
Of the 286 programs that responded to the survey, 61 (21%) responded to the item about shared frameworks (i.e., “Which frameworks related to technology, if any, do you share explicitly with students in these classes?”). These responses yielded a list of 23 different frameworks, ranging from theoretical frameworks (e.g., Technology Pedagogy and Content Knowledge [TPACK]), to state-specific standards (e.g., Ohio Learning Standards for Technology), to position statements from professional organizations (e.g., the National Council of Teachers of Mathematics [NCTM] 2015 Technology Position Statement).
Data Sources for the Frameworks
With a set of frameworks identified, we then set out to collect data related to each. In this situation, the data were collected from primary sources for each identified framework. For example, we noted how the framework was developed, for whom (e.g., teacher educators or practicing teachers), any figures used to represent it, and whether it was peer reviewed. Data collection was facilitated by the use of a Google form. The form provided prompts to guide the extraction of data from the sources and recorded and organized responses to these prompts in a spreadsheet.
Finally, precise summaries of each framework were constructed. Summary construction was an iterative process. First, a pair of research team members worked collaboratively to write a one- to two-page summary from the primary source. Based on this first iteration the team agreed upon the important features to include a clear description of the framework (including any figures), its original purpose (e.g., to inform or to describe), and identification of any work from which it is built.
Next, two researchers reviewed the summaries to make sure that all of the previously mentioned features were included. Any summaries that did not include all of those features were revised. Then the entire research team read each summary for consistency with the primary resources with any further refinements done as a group. At this time the summaries were approximately one page each. In an effort to focus on the goal of each of the frameworks (i.e., the phenomenon it is framing), summaries were abbreviated to brief descriptions that left out details about where the framework originated and how it was developed and only focused on what it framed. For example, our brief description of Pea’s (1985) framework stated,
Computers and technology are often viewed as amplifiers of cognition, in that they allow humans to perform tasks with increased speed and accuracy. Pea claimed that computers and technology can also act as reorganizers of cognition, in that technology can transform the way in which an individual views a concept or idea.
While teams of two led the construction of each summary and brief description, each was brought back to the team to work to ensure what was written aligned with the original resources. This process of refinement continued until we were confident both the summary and the brief description accurately reflected the original author’s work. In addition, one draft of the brief descriptions of each framework was vetted by other mathematics teacher educators in a conference session of the AMTE (Bailey et al., 2020). Feedback from that session, mostly focused on clarity not content, led to further refinement of the brief descriptions. (The framework summary cards can be downloaded from https://ptmt.s3.amazonaws.com/impact/Framework%20Cards.pdf)
Analysis
As expected, the survey prompt elicited a variety of responses, including some frameworks that were not specific to technology and some that were not aligned with the conceptualization of framing guiding this study. As an example of the latter, the Ohio Learning Standards indicate the expectation to integrate technology in instruction, but they do not frame a phenomenon related to learning or teaching mathematics with technology. To address this issue we removed the survey responses that did not meet the criterion of explicitly framing a phenomenon related to learning or teaching mathematics with technology (N = 6). This approach resulted in a set of 17 frameworks.
We open-coded the 17 framework brief descriptions to identify themes related to what was being framed by each. This coding was done through a sorting process in which framework descriptions (with no identifying features) were placed on virtual cards (using the card sort capabilities of the software program Desmos Activity Builder), and each member of the team sorted the cards into categories utilizing the guiding question, “What is being framed?”
The Desmos teacher dashboard “overview” feature for card sorts was utilized to identify commonalities among the sorting done by each member of the research team and to identify overarching themes among the frameworks (see Figures 2 and 3). (Our sorting allowed for frameworks to be placed in more than one category if appropriate.) This refining process resulted in four themes, each of which will be described in detail in the findings.
Figure 2 Sample Desmos Card Sort
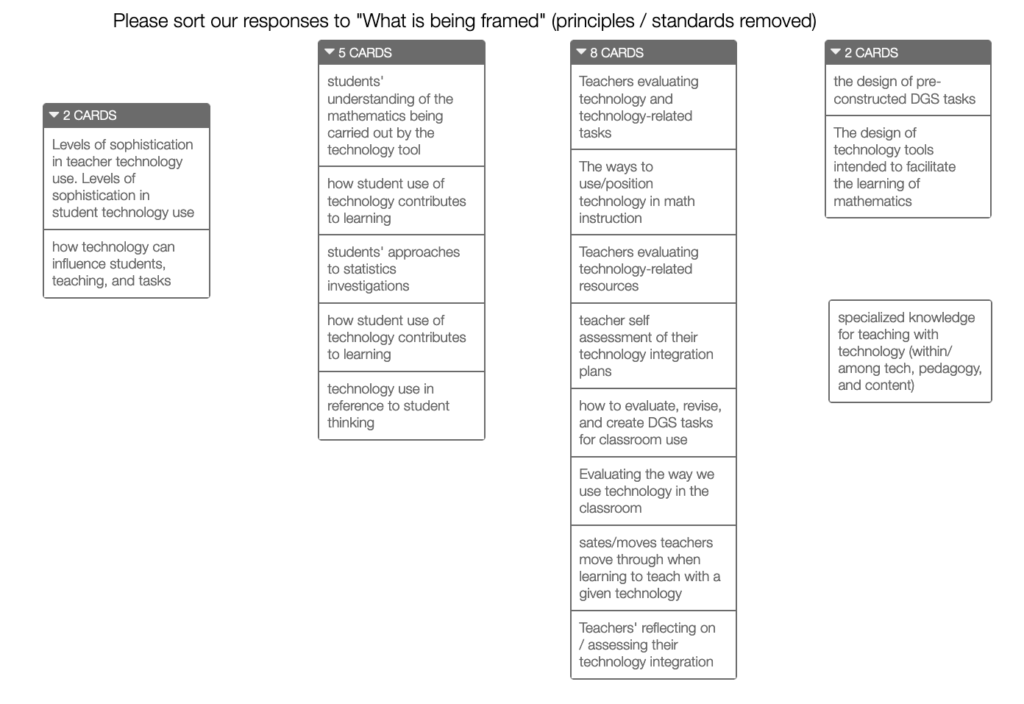
Figure 3 Overview of the Sample Desmos Card Sort

Findings
The 17 frameworks included in our analysis are, in essence, the answer to our first research question (What frameworks are MTEs using to frame their work related to teaching secondary mathematics teachers to teach with technology?). Of these 17 frameworks, all but one, the Substitution, Augmentation, Modification, and Redefinition (SAMR) model, have been peer reviewed. Examining the audience each was intended for, we found that 12 of the frameworks were derived from mathematics-specific contexts, with the remaining 5 originating from a broader perspective. The two most commonly submitted frameworks, TPACK (N = 13) and the SAMR model (N = 8) are not from mathematics-specific contexts.
By way of answering our second research question, the four resulting “what is being framed” categories are described (see Figure 4), beginning with the consideration of how students use and learn with technology. This category informs both the design and evaluation of technology tools and tasks and ways teachers use technology in instruction. These categories, in turn, inform the framing of how teachers learn to use technology for instruction.
Figure 4 Four Framing Categories Related to Preparing Teachers to Teach Mathematics With Technology
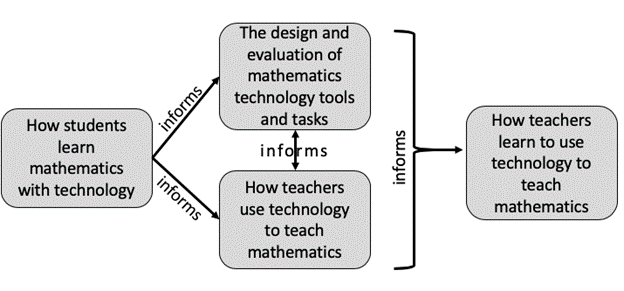
Framing How Students Learn Mathematics With Technology
This category, framing how students learn mathematics with technology, brings together a collection of frameworks that can be used to describe how students use technology in mathematics courses, the ways in which students learn with technology, and other cognitive dimensions of students’ technology use. Within this category, three of the five frameworks originated in mathematics-specific contexts (virtual cultural theory; master, servant, partner, extension of self, and white box/black box), and two frameworks are not mathematics-specific (activity theory and amplifier/reorganizer)
Virtual Cultural Theory
Shaffer and Kaput’s (1998) virtual cultural theory was based on the power of “computational media” (a term meant to better depict the impact of future computers to be transformational) to externalize, or cognitively off-load, significant pieces of algorithmic processing. By doing so, such technology affords the power to transform the way we approach mathematics. In a virtual culture, students will have innovative ways of sharing new forms of mathematical experiences, mathematical representations, and mathematical understanding. “The implications of virtual culture for mathematics education will be an increased emphasis on embedded and situated mathematics – on mathematics as a way of knowing the world rather than on mathematics as computation or mathematics as formal proof” (Shaffer & Kaput, 1998, p. 113).
Virtual cultural theory suggested that, as the nature of technology evolves, the nature of mathematical learning (and of mathematics itself) will also evolve. The most direct applications of the theory are to student use of technology to access and explore mathematics. As with other such theories, these possibilities have pedagogical implications for teachers who seek to allow or encourage their students to use technology in these ways.
Master, Servant, Partner, Extension-of-Self
Goos et al. (2000) analyzed teachers’ use of technology within mathematics lessons to theorize “four roles for the interaction between teacher and technology” (p. 307): Master, Servant, Partner, and Extension-of-self. We categorized this framework here (as well as in “how teachers use technology” category) because, as this work progressed, Goos et al. (2003) came to view these roles as metaphors that “are suggestive of different ways in which teachers and students [emphasis added] might appropriate technology into classroom mathematical practices” (p. 76).
These roles are viewed as hierarchical with respect to user knowledge and the potential use of a given technology: Technology as (a) Master – characterized by limited knowledge of a technology and dependent technology use; (b) Servant – some knowledge of a technology, but use is limited to supporting typical ways of thinking/working without technology; (c) Partner -increased knowledge of a technology and its use enhances mathematical learning; and (d) Extension-of-self – using mathematical and communication technologies as a natural part of mathematical work.
White Box/Black Box
Buchberger (1990) used a white box/black box metaphor to describe two contrasting ways of using technology to carry out mathematical calculations. Technology is a black box if the user does not already have an understanding of the mathematical calculations being carried out by the technology. By contrast, technology is a white box if the user does have that preexisting understanding. He proposed that, as a general principle, both teachers and students should use technology as a white box.
The field of mathematics education has viewed the metaphor itself as much more valuable than the proposed didactic principle (particularly, given the evidence that students can indeed develop robust understanding of a concept without being able to carry out associated procedures by hand; see, e.g., de Beer et al., 2017; Heid, 1988). The metaphor facilitates consideration of the affordances and constraints of using technology before, while, and after coming to understand mathematical ideas. For example, such consideration has led to expanding the dichotomy to thinking of what using technology as a “grey box” might mean (Cedillo & Kieran, 2003).
Activity Theory
Activity Theory is a collection of principles related to human activity that grew out of the work of Vygotsky (1978) and Leont’ev (1978; see also Engström et al., 1999; Nardi, 1996). It is sometimes referred to as tool oriented because of the central role that tools play in the theory as a mediating means. As explained by Liang et al. (2009), Activity Theory
uses activity as the basic unit for studying human practices and highlights the idea that the relationship between the subject and the object is not direct but rather mediated through the use of a tool. A tool can be something physical (e.g., wirelessly interconnected handhelds) or intellectual (e.g., rules and roles displayed on handhelds). (p. 393)
As a tool-oriented theory of learning, Activity Theory can be used as a framework for explaining how students learn mathematics using technology (see Nardi, 1996). As with other theories of learning, Activity Theory is not a theory of teaching, but it does have implications for designing learning environments.
Amplifier and Reorganizer
Pea (1985) described two metaphors to characterize technology use, amplifier and reorganizer. When used as an amplifier, technology is used to make students’ work more efficient and accurate by quickly performing calculations or computations and generating representations, but the nature of students’ thinking is not modified. In contrast, technology use as a reorganizer leverages the affordances of a given technology to shift students’ thinking in a way that would be difficult or impossible to achieve without technology. Pea’s metaphors focus on the cognitive processes of the learner (student), thus framing both the ways students learn with technology and how the affordances of technology relate to these ways.
Each of these frameworks can be used to explain some aspect of the role technology plays in technology-mediated mathematics learning. That said, not all of these theories are theories of learning per se. Some of these theories frame the nature of the activity (i.e., technology use) itself more so than the learning that may or may not result from that activity. Nevertheless, each of these frameworks has important implications for how teachers make decisions about the inclusion of technology within mathematics instruction. Knowing how students may use and learn with mathematics can inform the design of students’ opportunities to learn through the use of technology.
Framing the Design and Evaluation of Mathematics Technology Tools and Tasks
In the second category of frameworks, we identified those that frame the design and evaluation of mathematics technology tools and tasks. These frameworks are intended to guide teachers in the creation or curation of technology learning experiences or the evaluation of technology tools for use in secondary mathematics instruction.
The five frameworks in this category ranged from framing the design or evaluation of specific types of technology tools (e.g., dynamic geometry tools) to digital instructional resources, in general. All the frameworks in this category were developed in a mathematical context. In this category, the Design Principles for Pre-Constructed Dynamic Geometry Sketches framework is presented first to provide a description of how it influenced two other frameworks: Interactive Geometry Software Framework (IGS FW) and Dynamic Geometry Task Analysis.
Design Principles for Pre-Constructed Dynamic Geometry Sketches
Sinclair (2003) utilized preconstructed geometry sketches within tasks and described elements of the task, directions, and questions that afforded or constrained the students. Specifically, she studied student engagement with such tasks from two perspectives: (a) how students responded to particular question types and sketch provisions and (b) how particular results highlighted elements that were missing (and needed) or poorly designed. As a result of this work Sinclair offered up five design principles for activities that utilize dynamic geometry sketches (see Figure 5).
Figure 5 Design Principles for Preconstructed Dynamic Geometry Sketches

constructed, Dynamic Geometry Sketches and Accompanying Materials,“ by M.P. Sinclair,
2003, Educational Studies in Mathematics, 52(3), p. 312 (https:
//doi.org/10.10.1023/A:1024305603330). Copyright 2003 by Kluwer Academic Publishers.
Interactive Geometry Software Framework
Sherman and Cayton (2015) applied a research-based framework to a specific task and discussed how it can be used to evaluate and revise the task with respect to goals of student thinking. This particular framework was inspired by two studies: Sherman (2014), which examined how the use of technology was related to students’ mathematical thinking by examining secondary school mathematics teachers’ use of technology, and Cayton (2012), which used one-to-one Algebra 1 classes to study how teacher implementation of preconstructed interactive tasks influenced cognitive demand.
The Interactive Geometry Software (IGS) Framework combines Pea’s (1985) characterization of amplifier vs. reorganizer and Sincliair’s (2003) design principles in a two-dimensional array (as seen in Figure 6) to facilitate analysis of the use of interactive geometry within a task with respect to the goals of meaningful observation, exploration, and conjecture.
Figure 6 IGS Framework
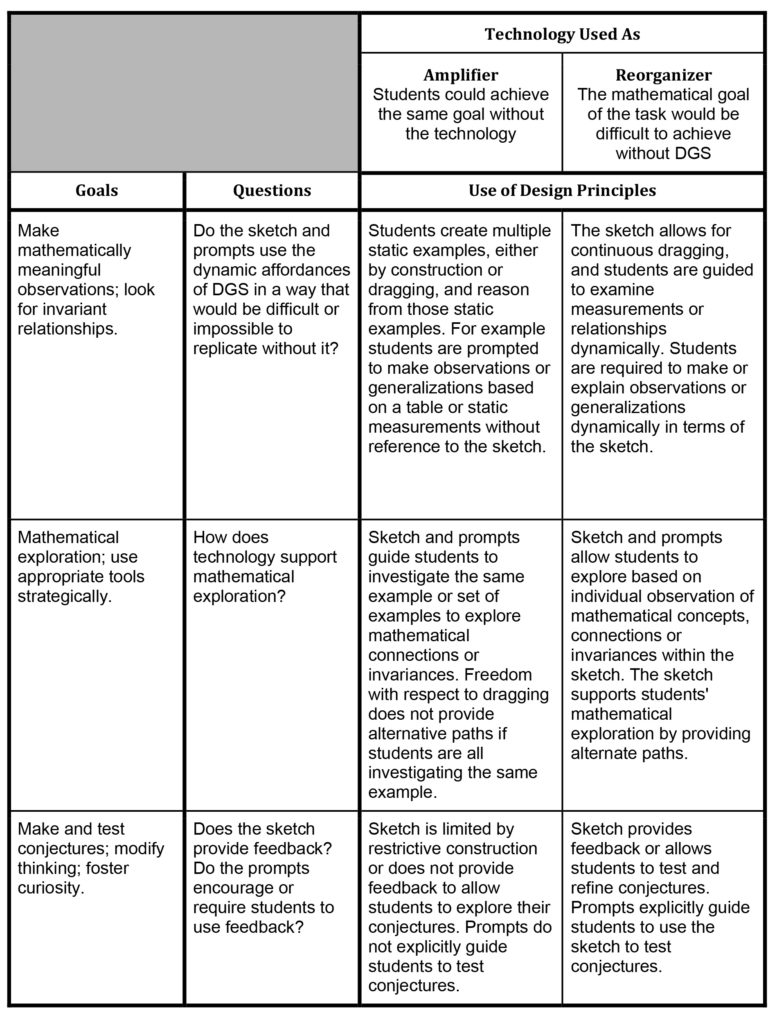
and C. Cayton, 2015, Mathematics Teacher, 109(4), p. 308
(https://doi.org/10.5951/mathteacher.109.4.0306). Copyright 2015 by National Council of
Teachers of Mathematics.
Dynamic Geometry Task Analysis
The Dynamic Geometry Task Analysis framework (Trocki, 2014), seen in Figure 7, outlines two dimensions for analyzing dynamic geometry tasks: (a) mathematical depth, drawing on cognitive demand (Smith & Stein, 1998), and (b) types of technological action, drawing on Sinclair (2003). These dimensions capture the extent to which a prompt or sketch allows for mathematical depth and the types of technological action required.
Figure 7 Dynamic Geometry Task Analysis
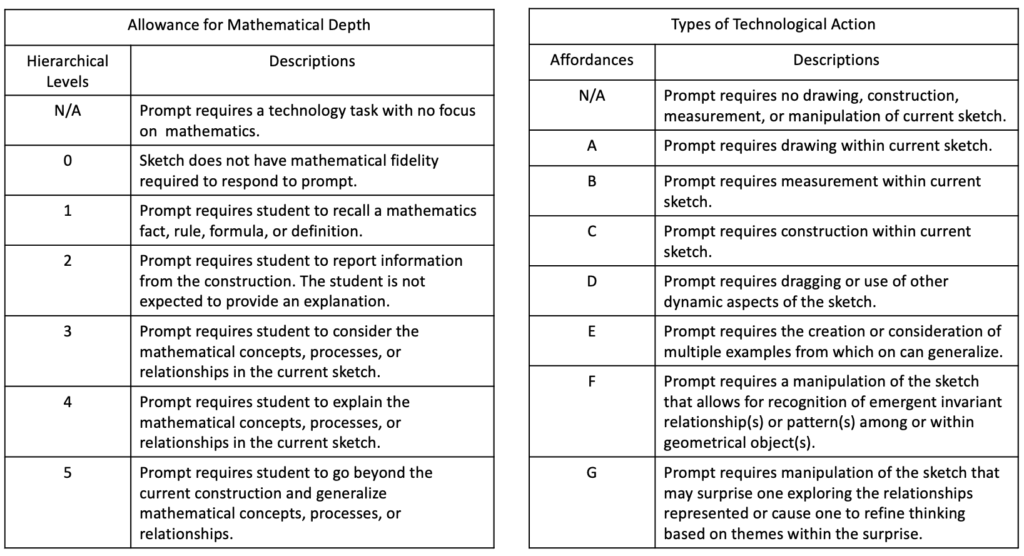
Trocki and Hollebrands (2018) classified a high-quality dynamic geometry mathematics task as one in which both the mathematical prompts and the technological actions combine to concentrate students on understanding concepts, processes, and relationships. A medium-level task contains a collection of prompts that coordinate mathematical depth and technological actions in a way that may encourage but does not necessitate that students reach generalized conclusions based on emergent invariant relationships that go beyond a static sketch. A low-level task does not contain a collection of prompts that coordinate mathematical depth and technological actions in a way that requires students to make generalized conclusions based on emergent invariant relationships that go beyond a static sketch.
Pedagogical, Mathematical, and Cognitive Fidelity
Dick (2008) proposed three types of fidelity (pedagogical, mathematical, and cognitive) that could be used to evaluate how true the design of technological tools is to the learning and teaching of mathematics those tools were designed to facilitate. Pedagogical fidelity is characterized by the extent to which students are likely to view a technological tool as “(a) facilitating the creation of mathematical objects, (b) allowing mathematical actions on those objects, and (c) providing clear evidence of the consequences of those actions” (p. 334). In other words, technological tools are pedagogically faithful when their interface clearly and transparently allows the user to enact and perceive mathematical actions, a primary pedagogical intent of teaching mathematics with technological tools.
Mathematical fidelity is characterized by the accuracy and comprehensiveness of a tool with respect to the properties and definitions of whatever mathematical concepts the tool is designed to represent. Technological tools are mathematically faithful when the technological representations of and actions on a concept are in harmony with the way that concept is viewed by the mathematics community. Students need to be able to use the tool in ways that are consistent with the ways they construct the mathematics.
Cognitive Fidelity is characterized by the extent to which the actions the tool allows align with the cognitive actions of the user. Tools are cognitively faithful when they enable students to enact explicitly with the tool various actions or schemas that are associated with a given mathematical concept.
Framework for Evaluating Digital Instructional Materials
Building on both the Replacement, Amplification, and Transformation (RAT) framework (Hughes et al., 2006) and NCTM’s (2014) eight effective mathematics teaching practices, Thomas and Edson (2017, 2019) introduced the research-based Digital Instructional Materials (DIM) framework to help teachers evaluate digital resources for use in the classroom. They conceptualized digital instructional materials to be at the cross-section of curriculum materials and technology and to include the full range of digital forms of instructional resources, from digital textbooks to mathematics action technologies. Using a two-dimensional matrix (for an excerpt, see Figure 8), the DIM framework describes what each category of technology use would look like for each of the eight teaching practices.
Figure 8 Excerpt of the DIM Framework
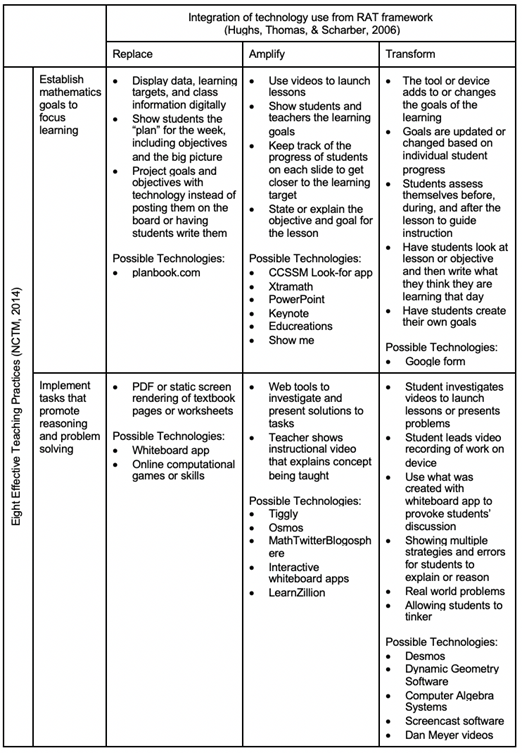
Instructional Materials: Integrating Mathematics Teaching Practices With Technology Use in K-8 Classrooms,” by A. Thomas & A. J. Edson, 2017, Contemporary Issues in Technology and Teacher Education, 19(3) (https://citejournal.org/volume-19/issue-3-19/mathematics/a-framework-for-teachers-evaluation-of-digital-instructional-materials-integrating-mathematics-teaching-practices-with-technology-use-in-k-8-classrooms). Copyright 2017 by A. Thomas and A. J. Edson.
The intent of the DIM framework is to guide teachers in their technology integration choices. This newly developed framework was found to be useful by the K-8 teachers that were part of its development, but to date it has not been tested more widely.
The five frameworks presented in this category may be effective in helping teachers choose and design technology-based tasks. In that same regard, it could show value for MTEs by providing a lens for preservice teachers to evaluate what constitutes high-quality technology tools and tasks. Excluding the Design Principles for Pre-Constructed Dynamic Geometry Sketches Framework, all in this category contain criteria about the technology’s ability to maintain mathematical fidelity and keep mathematical goals at the forefront of the task. This thread of common criteria suggests that MTEs could utilize any of these frameworks to ensure teachers keep mathematical fidelity as a focus when curating and designing technology-based tasks.
Framing How Teachers use Technology to Teach Mathematics
The third category of frameworks we identified were those that frame how teachers use technology during mathematics instruction and evaluate that use. These six frameworks were designed to aid teachers in planning technology integration and in assessing how they are using technology within their classrooms. The first three frameworks (the Didactic Tetrahedron; Master, Servant, Partner, Extension of Self; Orchestration Types) were derived from mathematics-specific contexts; the remaining three frameworks (PIC-RAT, SAMR, and TIP) were derived from the broader context of learning and teaching with technology.
The Didactic Tetrahedron
Cohen et al. (2003) presented a model, the instructional triangle, in which they described mathematics teaching practices in terms of the interactions among the teacher, students, and content. Hollebrands (2017) built upon this work by adding a fourth dimension to consider the ways in which the use of technology mediates the interactions among the teacher, students, and mathematics task (see Figure 9).
Figure 9 The Didactic Tetrahedron
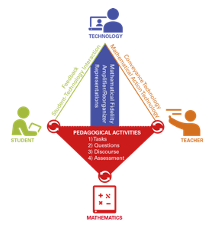
courses.s3.amazonaws.com/tmt/unit_5/FrameworkMath-TechMOOC_REVISED.pdf) In the public domain.
Master, Servant, Partner, Extension of Self
As mentioned previously, Master, Servant, Partner, and Extension of Self are metaphors used to describe technology use in mathematics classrooms by both students and teachers (Goos et al., 2000). With respect to teacher use, the role of Master indicates minimal technology use in the classroom because of limited teacher knowledge. The role of Servant describes when the teacher utilizes technology in a limited way with little attempt to change the nature of mathematical tasks or students’ interactions with those tasks. When teachers use technology as a Partner, they leverage their greater knowledge of technology to enhance the quality of students’ mathematical learning. The role of Extension of Self occurs when a teacher’s extensive knowledge allows them to incorporate technology in instruction in powerful yet natural ways.
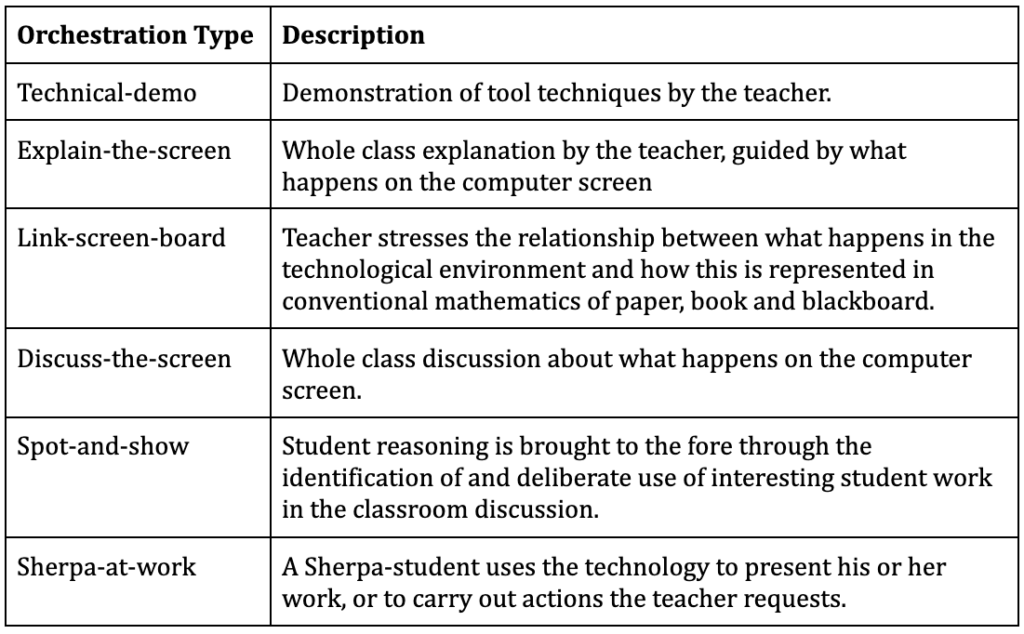
Orchestration Types
Drijvers et al. (2010) reported on six orchestration types that teachers demonstrated when using a java applet in their classrooms to teach the concept of function: Technical-demo, Explain-the-screen, Link-screen-board, Discuss-the-screen, Spot-and-show, and Sherpa-at-work (see Figure 10). The first three orchestration types are considered to be more teacher-centered orchestrations, and the last three more student-centered.
Figure 10 Description of Drijvers et al.’s (2010) Orchestration Types
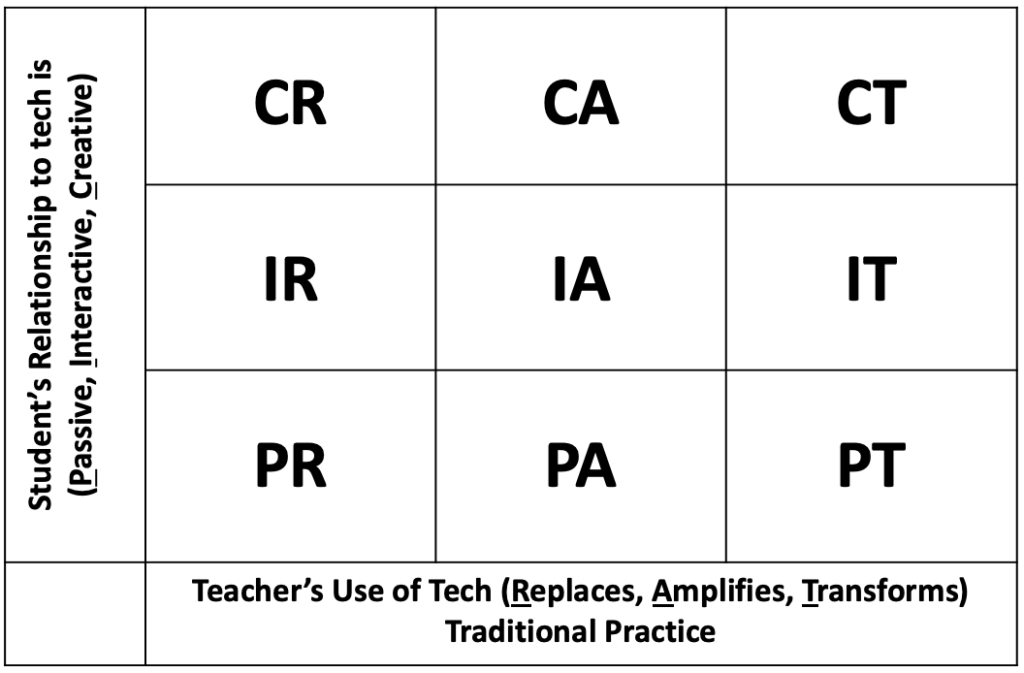
The PIC-RAT Framework
The PIC-RAT framework is an array with two dimensions: student use (Passive, Interactive, or Creative [PIC]) and teacher use (Replacement, Amplification, and Transformation [RAT]). Kimmons (2016) built upon the work of Hughes et al. (2006), who developed the RAT framework, which was designed to help in-service and preservice teachers make decisions about technology implementation. They drew on the work of Pea (1985) to define replacement, amplification, and transformation as the action on student learning, instructional practices or content goals. Kimmons argued that one progresses from the lower left corner (see Figure 11) or the PR section of the array toward the top right corner or CT section.
Figure 11 The PIC-RAT Framework
The SAMR Model
Puentedura (2006) developed the SAMR model to provide science teachers with an approach to selecting, using, and evaluating technology (Figure 12 shows the four-step heirarchy). The Substitution level is similar to replacement in Hughes et al.’s (2006) RAT framework, in that technology is being used to replace or substitute ordinary actions. If the technology were removed, no real difference in the learning goal would occur.
Figure 12 The SAMR Model

At the Augmentation level technology use affords some benefits, despite the actions remaining the same. At the Modification level, technology is used to significantly redesign a task, redesign that could not have happened without the technology tool. The Redefinition level is achieved when the task itself cannot exist without the employment of that technology. Substitution and Augmentation are considered stages that enhance a teacher’s practice, whereas Modification and Redefinition are considered stages that transform a teacher’s practice.
The Technology Integration Planning Model
The Technology Integration Planning (TIP) Model described seven steps organized into three phases (see Figure 13) related to selecting, planning, implementing, and evaluating technology use (Roblyer & Doering, 2010). In the first phase, teachers consider learning needs and the potential that technology integration holds in addressing those needs. The goal of this phase is to clearly define the learning problem, identify a solution, consider the relative advantage of using technology, and finally, determine what resources are necessary to implement the solution.
The second phase deals with the logistics of implementation, including creating clearly defined learning goals, attending to how to evaluate those goals, and considering what instructional approach best aligns with the technology use and how to prepare students to successfully engage with the technology. The third phase focuses on assessing the technology integration. The goal of this final phase is to assess the evidence that students reached the learning goal and consider how to improve the lesson for future use.
Figure 13 The TIP Model
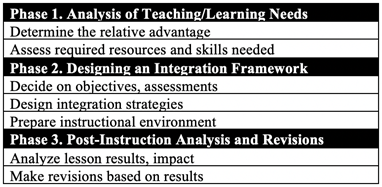
While these six frameworks broadly address some stage of planning for technology integration and often employ a hierarchical structure, they differ in whether they attend to both use and evaluation of technology. Some are more general guidelines for planning for technology integration (e.g., The TIP Model), while others aim to consider the ways in which teachers position the technology in conjunction with learning mathematics (e.g., PIC-RAT and The SAMR Model).
Framing How Teachers Learn to Use Technology to Teach Mathematics
The final category of frameworks we identified were those that frame how teachers learn to use technology for teaching mathematics. These frameworks describe the specialized knowledge that teachers need for teaching mathematics with technology and how they develop that knowledge. Such frameworks are not necessarily intended for use by teachers, but they can be useful to guide the design of learning experiences (i.e., courses or professional development) or to inform research that includes identifying or developing teachers’ knowledge for teaching mathematics with technology. The two frameworks that fell into this category – TPACK and Play, Use, Recommend, Incorporate, and Assess (PURIA) – are described in the following section.
Technological Pedagogical and Content Knowledge
The TPACK framework describes the specialized knowledge needed to teach with technology (Mishra & Koehler, 2006). TPACK is an expansion of Shulman’s (1986) pedagogical content knowledge (PCK), which described the intersection of knowledge of content and knowledge of teaching. TPACK, as described by Mishra and Koehler, asserts that effective teachers rely on the integration of multiple domains of knowledge: deep understanding of the content (e.g., mathematics), deep understanding of pedagogy, and a deep understanding of technology (see Figure 14).
Figure 14 The TPACK Framework
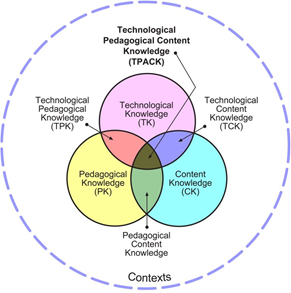
In the case of mathematics, Niess (2005) and Niess et al. (2009) adapted Grossman’s (1989, 1990) proposed components of PCK to take technology into consideration. Neiss et al.’s (2009) adaptation included using the elements of the framework to outline the outcomes of TPACK knowledge:
(1) an overarching conception about the purposes for incorporating technology in teaching mathematics; (2) knowledge of students’ understandings, thinking, and learning of mathematics with technology; (3) knowledge of curriculum and curricular materials that integrate technology in learning and teaching mathematics; (4) knowledge of instructional strategies and representations for teaching and learning mathematics with technologies. (p. 8)
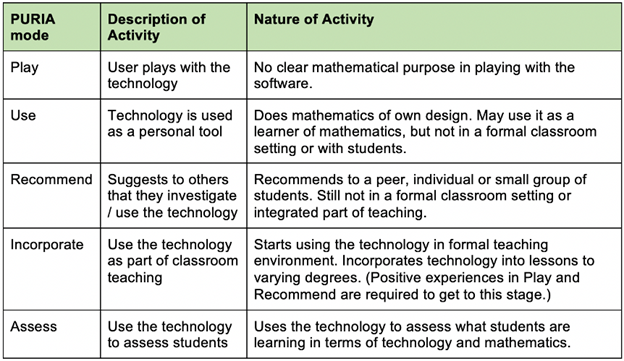
The PURIA Model
The PURIA model (Beaudin & Bowers, 1997) describes developmental phases teachers go through to become confident teachers of mathematics with technology. Originally conceived as a way to describe how teachers learn to integrate computer algebra systems (CAS) into their teaching, the model was later expanded by Zbiek and Hollebrands (2008) to include all mathematics action tools. Each stage is described in Figure 15.
Figure 15 The PURIA Model
Mathematics Teachers’ Processes for Making Sense of Students’ Work with Technology,” by R.
M. Zbiek and K. Hollebrands, 2008. Research on Technology and the Teaching and Learning of Mathematics 1, 287-344. Copyright 2008 by National Council of Teachers of Mathematics.
In this model, teachers develop through using technology in one mode until they are comfortable enough to go on to the next mode of use. Stages can overlap and are traversed at different rates depending on the aptitude of the user. Zbiek and Hollebrands (2008) noted that PURIA is useful for understanding “not only how teachers’ understandings grow but also why teachers’ personal technology use and classroom practice may differ greatly” (p. 334).
In summary, the two frameworks in this category are different, but complimentary. TPACK describes knowledge needed to teach mathematics with technology and PURIA is a process one might go through to develop that knowledge.
Implications for Mathematics Teacher Educators
The findings from this study provide an overview of the ways the work of MTEs related to the preparation of teachers to teach mathematics with technology both is and is not being framed. The MTEs who responded to this item on the survey all listed frameworks well aligned with the work of preparing teachers to teach with technology. While some frameworks were elicited that were not framing particular phenomena (e.g., Ohio Learning Standards for Technology), they were all in some way related to teaching and learning with technology. Focusing on the 17 frameworks that were framing a phenomenon, and hence were included in this study, approximately three quarters of them were derived from mathematics specific contexts. However, the two most commonly elicited frameworks, TPACK (21%) and the SAMR model (12%), were not. These results lead us to reflect on not only what is being framed by this collection of frameworks, but also what might be missing.
What Is Being Framed?
Our analysis of the 17 frameworks was guided by identifying the phenomena related to teaching mathematics with technology that were being framed. From this lens, we identified four categories:
- How students use and learn with technology.
- The design and evaluation of technology tools and tasks.
- How teachers use technology.
- How teachers learn to use technology.
Two to seven frameworks fit in each category (see Figure 16), with a variety coming from mathematics-specific contexts and nonmathematics-specific contexts across the four.
Figure 16 List of Frameworks by Category

Approximately half of the frameworks in the “How students use and learn with technology” and “How teachers use technology” categories did not originate in a mathematics-specific context. Those that did not originate in mathematics contexts often originated in general education contexts instead. In contrast, all of the frameworks related to the design and evaluation of technology-based tasks were developed in a mathematics-specific context.
This result makes sense, as these frameworks are related to mathematics-specific technology tools. In fact, some of the frameworks in this category were related to very specific tools. For example, three of the six are specific to dynamic geometry software. It is worth considering the benefit of both more and less specific frameworks in this category. As mathematics-specific tools have broadened to include more than dynamic geometry spaces (e.g., Desmos Activity Builder), having frameworks to guide the selection or adaptation of their use would be helpful to teachers. That said, frameworks specific to particular software capabilities might be more helpful in guiding the work of curriculum designers working to incorporate such technology tools in meaningful ways.
Reflecting on the frameworks that MTEs are using that are not mathematics specific, we wonder what benefit there may be in adapting them for mathematics specific contexts. For example, TPACK started as a framework to describe knowledge to teach with technology broadly (Mishra & Koehler, 2006). Neiss (2005) and Neiss et al. (2009) then adapted it to frame knowledge for teaching science and mathematics specifically.
Others have since adapted it to be even more specific, focusing on knowledge to teach statistics (Lee & Hollebrands, 2011) and functions (Lovett et al., 2020) with technology. Such specified frameworks have proven useful for the development of both curricula and research activities related to the teaching of mathematics and statistics with technology (e.g., Ayieko et al., 2019; Lee & Hollebrands, 2008; Lee & Hollebrands, 2011; Lovett, et al., 2020; Niess, et al., 2009).
That all but one of the frameworks in this study has been peer reviewed is encouraging. Our work as MTEs should be guided by research (AMTE, 2017). Knowing a framework has gone through a rigorous review process provides MTEs’ confidence in its usefulness and insight into ways it can guide various aspects of our work.
The only framework submitted that has not gone through the peer review process is The SAMR Model. In fact, this framework has been criticized for having not gone through peer review, and its shortcomings are well documented (Hamilton et al., 2016). Yet both our findings here and those of Hamilton et al. (2016) indicate that it is widely used across a variety of settings.
This wide use suggests something about the framework is useful to MTEs. It may simply be that the SAMR model has appeared in more visible venues, so more people are aware of it, or maybe it offers something that other frameworks do not. For example, the primary source for the SAMR model is a presentation created by the head of an educational consulting firm (Hippasus). This presentation has been disseminated widely through paid professional development sessions at both the school and district level (Puentedura, 2006), possibly making it more visible to teachers and professional developers than are frameworks disseminated through peer reviewed journals. Determining the reasons for its popularity would be fruitful, as such findings could guide the ways in which frameworks intended for use with teachers are communicated.
What Is Not Being Framed?
Given our findings related to what is being framed, we find it prudent to step back and consider phenomena related to MTEs’ work to prepare PSMTs to teach mathematics with technology that is not being framed. To do so, we compared the resulting collection of 17 frameworks with the aspirational goals outlined in the AMTE (2017) SPTM related to teaching with technology (see Figure 17).
Figure 17 Framing the Goals for Preparing Teachers to Teach Mathematics With Technology
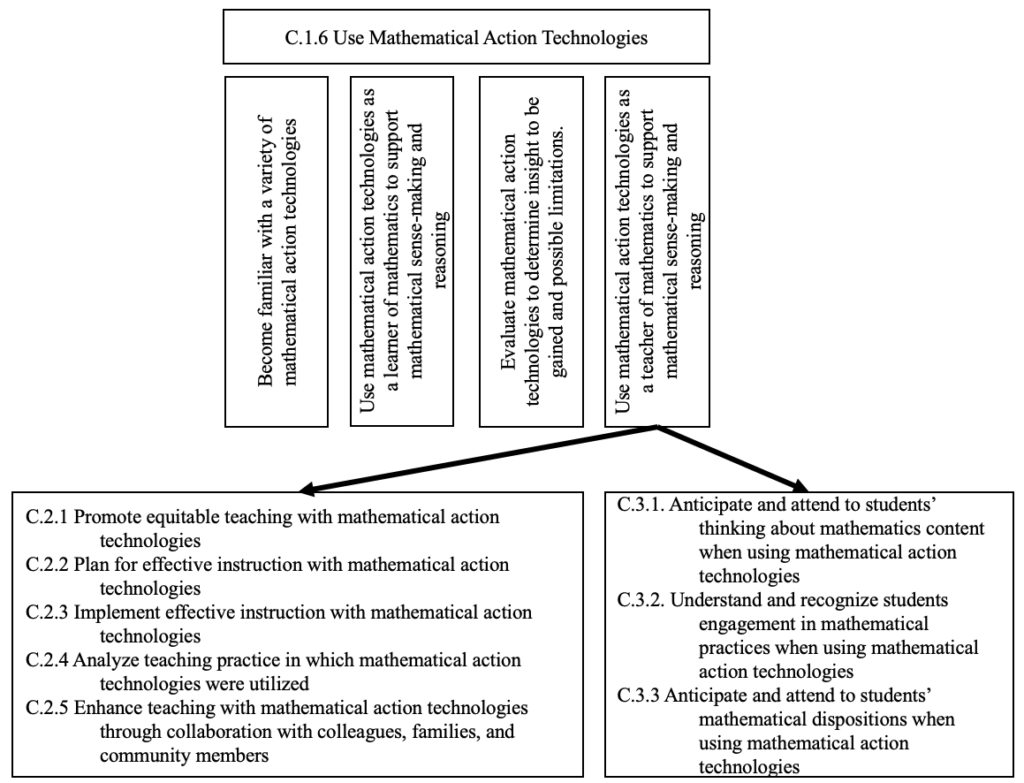
One of the first things we notice across all categories was that equity issues are not explicitly addressed in any of the frameworks in this sample. While the language in some of the frameworks seems to provide space for considering issues of equity, none specifically frame issues related to equity to inform teaching and learning with technology. For example, when considering the framing of work related to designing and evaluating tasks, not only would you expect attention to the ways the task connects to students’ personal assets broadly, but also specifically related to the technology (e.g., is the task accessible based on prior technology experiences? AMTE, 2017).
Furthermore, issues of equity should inform decisions about technology use as it relates to access, yet none of the frameworks in this sample address how decisions are made regarding when and what to use. In a study of 21 technology-using early career mathematics teachers, McCulloch et al. (2018) found regularity among the criteria teachers consider when deciding whether to incorporate technology into a lesson and, when deemed appropriate, for deciding which technology tool to use. Many of the criteria noted were related to issues of access (e.g., Does the tool work on a variety of platforms? Does it have to be downloaded? Do students need to have an account to use it?). These findings suggest that a framework to guide such teacher decisions would be useful. (For an example of an equity-related framework for technology use in the classroom, see Damarin, 2000.)
Another area of work noticeably missing among this group of frameworks is attention to the ways that eliciting and using student thinking differs when students are using mathematics action technologies compared to when they are not. Many researchers have observed that the ways students interact with a technology tool, especially a dynamic mathematics tool, can provide insight to student thinking (e.g., Azarello et al., 2002; Doerr & Zangor, 2000; McCulloch, 2011; Wilson et al., 2011). These observations, coupled with recent research that points to the importance of PSMTs’ developing the skill of professional noticing of students’ mathematical thinking (Jacobs & Spangler, 2017), suggest a need for framing the noticing of student mathematical thinking when using technology.
We briefly mention one other noticeably missing intersection of technology and mathematics education missing in this collection of frameworks: classroom mathematics discourse. A great deal of attention has been paid in the past few decades to the critical role discourse can play in the learning of mathematics (Herbel-Eisenmann et al., 2017) and, with that emphasis, explorations into the ways technology can influence that discourse (see Leatham & Barton, 2017). Promising directions in this area include work by Anderson-Pence (2017) and adapting existing mathematics discourse frameworks, such as Adler and Ronda (2015).
Conclusion
While our findings provide a helpful snapshot of the ways MTEs are framing the work related to teaching PSMTs to teach with technology, this study has limitations. The sample of frameworks we examined were not drawn systematically from the complete set of frameworks available for such work, rather they were offered by participants who completed a particular item on the survey: “Which frameworks related to technology (if any) do you share explicitly with students in these classes?” The wording of this item limited the responses to frameworks MTEs use with their PSMTs, thus, not providing a full picture of the frameworks that might be informing their work as a whole. For example, the category of framing how teachers learn to use technology only has two responses, likely due to this wording, as such frameworks guide the work of MTEs but might not be shared explicitly with PSMTs.
Our analysis of this collection of frameworks was guided by our research questions. As such, we focused on the phenomenon each was framing. However, if we had asked a different question, we might have categorized them differently. For example, one might think about whose work each framework was intended to inform (e.g., MTEs designing learning experiences for PSTs or PK-12 teachers designing instruction for their students).
Another possibility would be to examine the frameworks in reference to whether they are descriptive (models of what happened) versus prescriptive/aspirational (models of what should happen). This possibility brings up a critical point related to our decision to write our summaries based on the original use of a given framework.
Our summaries did not take into account how these frameworks might be used beyond their originally stated intent. For example, within the category of “Framing how teachers use technology”, Drijvers et al. (2010) described six technology orchestration types that teachers were observed using during instruction, which reports on models of what happened with technology use during instruction. However, the potential exists for MTEs to use this framework with PSMTs to educate them on which orchestration types should be the focus of teachers’ technology use during instruction.
In any of these scenarios, we hypothesize that themes may not be mutually exclusive. In fact, within the themes from our results Master, Partner, Servant, Extension of Self (Goos et al., 2000) was highlighted in both “How students use and learn with technology” and “How teachers use technology.” We would encourage fellow researchers, not only to think about different ways of examining the frameworks highlighted in this paper, but also to consider potential uses beyond the original purpose.
Furthermore, other areas of MTEs’ work related to preparing PSMTs to teach with technology likely exist that are neither captured by this study nor apparent in the mathematics teacher education literature. For example, we do not have frameworks to guide the complex interplay among providing PSMTs experience learning with technology, designing and evaluating tasks and instruction, and actually teaching with technology. In other words, given frameworks that frame student learning, teaching, and learning to teach mathematics with technology, what we do not seem to have yet are those for framing the teaching of mathematics teachers. Such a framework would likely draw heavily on frameworks like those discussed in this paper but would need to frame the work of MTEs (see Figure 18).
Figure 18 Framing the Work of MTEs to Prepare Teachers to Teach Mathematics With Technology
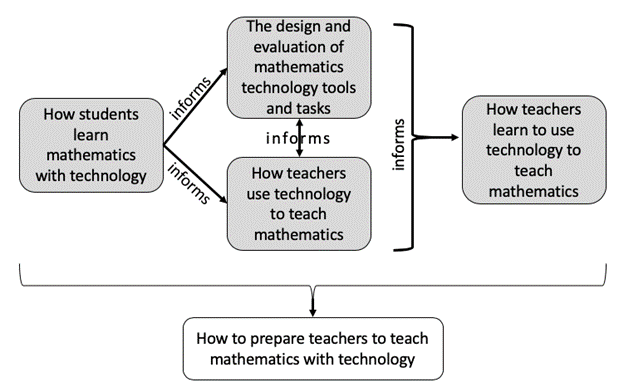
As our collective work toward preparing teachers to teach mathematics with technology continues to progress, it is important to consider the ways we are “using tools and frameworks grounded in research to develop core pedagogical practices” (AMTE, 2017, p. 35). In this study we utilized the frameworks identified by a survey of all accredited U.S. secondary mathematics teacher preparation programs to begin a conversation about the frameworks specific to this work that have emerged, as well as those that might still be needed. The findings from this study indicate a robust collection of frameworks that MTEs use in their instruction related to ways students’ use and learn with technology, ways teachers use technology, and selecting, evaluating, and adapting technology based tasks. However, fewer frameworks are related to ways teachers learn to use technology in their instruction (although the small numbers of such frameworks in our results may have been due to the focus of the survey prompt).
As we noted at the beginning of this paper, comparing and contrasting frameworks to identify overlaps and gaps are important tasks (Lester, 2005). We began that work here, noting overlaps, like the multiple frameworks specific to the design and evaluation of dynamic geometry tasks, and gaps, like the lack of explicit attention in these frameworks to issues of access and equity.
Future work focused on reconciling differences among overlapping frameworks as well as addressing identified gaps is necessary if these frameworks are going to guide work with PSMTs toward achieving the AMTE SPTMs. In addition, the findings here suggest that we are poised to consider how the frameworks in the four categories identified in this study could together inform an overarching framework (see Figure 18) for the work of MTEs in preparing secondary mathematics teachers to teach with technology.
Acknowledgements
We thank those who attended and participated in our AMTE 2020 session titled, “Theoretically Framing the Pedagogy of Learning to Teach Mathematics With Technology” for thinking critically about these frameworks with us. Support for this work was partially supported by the National Science Foundation under Grant No. DUE 1821054 awarded to University of North Carolina at Charlotte, Grant No. DUE 1820998 awarded to Middle Tennessee State University, and Grant No. DUE 1820967 awarded to East Carolina University. Any opinions, findings, and conclusions or recommendations expressed herein are those of the principal investigators and do not necessarily reflect the views of the National Science Foundation.
References
Adler, J., & Ronda, E. (2015). A framework for describing mathematics discourse in instruction and interpreting differences in teaching. African Journal of Research in Mathematics, Science and Technology Education, 19(3), 237-254. https://doi.org/10.1080/10288457.2015.1089677
Anderson-Pence, K. L. (2017). Techno-mathematical discourse: A conceptual framework for analyzing classroom discussions. Education Sciences, 7(1), 40. https://doi.org/10.3390/educsci7010040
Association of Mathematics Teacher Educators. (2017). Standards for preparing teachers of mathematics. amte.net/standards
Arzarello, F., Olivero, F., Paola, D., & Robutti, O. (2002). A cognitive analysis of dragging practices in Cabri environments. ZDM, 34(2), 66-72. https://doi.org/10.1007/BF02655708
Ayieko, R. A., Gokbel, E. N., & Akçay, A. O. (2019). Building knowledge for technology integration in learning to teach secondary school mathematics: Building technology knowledge. In M. L. Niess, H. Gillow-Wiles, & C. Angeli (Eds.) Handbook of research on TPACK in the digital age (pp. 24-26). IGI Global. https://doi.org/10.4018/978-1-5225-7001-1.ch002
Bailey, N., McCulloch, A.W., Leatham, K.R., Lovett, J.N., Cayton, C., Reed, S., & Fye, K. (2020, February 6-8). Theoretically framing the pedagogy of learning to teach mathematics with technology [Conference presentation]. Twenty-fourth annual meeting of the Association of Mathematics Teacher Educators, Phoenix, AZ, United States.
Beaudin, M., & Bowers, D. (1997). Logistic for facilitating CAS instruction. In J. Berry, J. Monaghan, M. Kronfellner, & B. Kutzler (Eds.), The state of computer algebra in mathematics education (pp. 216-135). Chartwell-Bratt.
Buchberger, B. (1990). Should students learn integration rules? ACM SIGSAM Bulletin, 24(1), 10-17. https://doi.org/10.1145/382276.1095228
Cayton, C. (2012). Examining the cognitive demand of tasks in three technology-intensive high school algebra 1 classrooms. In L. V. Van Zoest, J. Lo, & J. L. Kratky (Eds.), Proceedings of the thirty-fourth annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education-North America Chapter (pp. 865–868). Western Michigan University.
Cedillo, T., & Kieran, C. (2003). Initiating students into algebra with symbol-manipulating calculators. In J. T. Fey, A. Cuoco, C. Kieran, L. McMullin, & R. M. Zbiek (Eds.), Computer algebra systems in secondary school mathematics education (pp. 219-239). National Council of Teachers of Mathematics.
Cohen, D.K., Raudenbush, S.W., & Ball, D.L. (2003). Resources, instruction, and research. Educational Evaluation and Policy Analysis, 25(2), 119-142. https://doi.org/10.3102/01623737025002119
Damarin, S. (2000). The “digital divide” versus digital differences: Principles for equitable use of technology in education. Educational Technology, 40(4), 17-22.
de Beer, H., Gravemeijer, K., & van Eijck, M. (2017). A proposed local instruction theory for teaching instantaneous speed in grade five. The Mathematics Enthusiast, 14(1), 435-468.
Dick, T. P. (2008). Keeping the faith: Fidelity in technological tools for mathematics education. In G. W. Blume & M. K. Heid (Eds.), Research on technology and the teaching and learning of mathematics: Vol. 2. Cases and perspectives (pp. 333–339). Information Age.
Doerr, H., & Zangor, R. (2000). Creating meaning for and with the graphing calculator. Educational Studies in Mathematics, 41(2), 143-163. https://doi.org/10.1023/A:1003905929557
Drijvers, P., Doorman, M., Boon, P., Reed, H., & Gravemeijer, K. (2010). The teacher and the tool: Instrumental orchestrations in the technology-rich mathematics classroom. Educational Studies in Mathematics, 75, 213-234. https://doi.org/10.1007/s10649-010-9254-5
Engström, Y., Miettinen, R., & Punamäki, R. L. (Eds.). (1999). Perspectives on activity theory. Cambridge University Press.
Goos, M., Renshaw, P., Galbraith, P., & Geiger, V. (2000). Reshaping teacher and student roles in technology-enriched classrooms. Mathematics Education Research Journal, 12(3), 303-320. https://doi.org/10.1007/BF03217091
Goos, M., Galbraith, P., Renshaw, P., & Geiger, V. (2003). Perspectives on technology mediated learning in secondary school mathematics classrooms. The Journal of Mathematical Behavior, 22(1), 73-89. https://doi.org/10.1016/S0732-3123(03)00005-1
Grossman, P.L. (1989). Learning to teach without teacher education. Teachers College Record, 91(2), 191-208.
Grossman, P. L. (1990). The making of a teacher: Teacher knowledge and teacher education. Teachers College Press.
Hamilton, E., Rosenberg, J., & Akcaoglu, M. (2016). The substitution augmentation modification redefinition (SAMR) model: A critical review and suggestions for its use. TechTrends, 60(5), 433–441. https://doi.org/10.1007/s11528-016-0091-y
Heid, M. K. (1988). Resequencing skills and concepts in applied calculus using the computer as tool, Journal for Research in Mathematics Education, 19(1), 3-25. https://doi.org/10.2307/749108
Herbel-Eisenmann, B., Meaney, T., Bishop, J. P., & Heyd-Metzuyanim, E. (2017). Highlighting heritages and building tasks: A critical analysis of mathematics classroom discourse literature. In J. Cai (Ed.), Compendium for research in mathematics education (pp. 722-765). National Council of Teachers of Mathematics.
Hollebrands, K. (2016). The use of technology in the teaching and learning of mathematics framework. https://fi-courses.s3.amazonaws.com/tmt/unit_5/FrameworkMath-TechMOOC_REVISED.pdf
Hollebrands, K. (2017). A framework to guide the development of a teaching mathematics with technology massive open online course for educators (MOOC-ED). In E. Galindo & J. Newton (Eds.), Proceedings of the 39th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 80-89). Hoosier Association of Mathematics Teacher Educators.
Hughes, J., Thomas, R., & Scharber, C. (2006). Assessing technology integration: The RAT-replacement, amplification, and transformation-framework. In C. Crawford, R. Carlsen, K. McFerrin, J. Price, R. Weber & D. Willis (Eds.), Proceedings of SITE 2006-Society for Information Technology & Teacher Education International Conference (pp. 1616-1620). Association for the Advancement of Computing in in Education. https://www.learntechlib.org/primary/p/22293/
Jacobs, V. R., & Spangler, D. A. (2017). Research on core practices in K-12 mathematics teaching. In J. Cai (Ed.), Compendium for research in mathematics education (pp. 766 – 792). National Council of Teachers of Mathematics.
Kastberg, S., Sanchez, W., Edenfield, K., Tyminski, A., & Stump, S. (2012). What is the content of methods? Building an understanding of frameworks for mathematics methods courses. In L. R. Van Zoest, J. J. Lo, & J. L. Kratky (Eds.), Proceedings of the 34th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 1259-1267). Western Michigan University.
Kastberg, S. E., Tyminski, A. M., Lischka, A. E., & Sanchez, W. B. (Eds.). (2017). Building support for scholarly practices in mathematics methods. Information Age.
Kersaint, G., Horton, B., Stohl, H., & Garofalo, J. (2003). Technology beliefs and practices of mathematics education faculty. Journal of Technology and Teacher Education, 11(4), 549-577. https://doi.org/10.1007/s10734-013-9678-9
Kimmons, R. (2016). K-12 technology integration: A conceptual primer. https://k12techintegration.pressbooks.com/app/uploads/sites/47296/2016/09/K-12-Technology-Integration-1474477952.pdf
Leatham, K.R. (2006, January 26-28). A characterization of the preparation of preservice mathematics teachers to teach mathematics with technology [Conference presentation]. Tenth Annual Conference of the Association of Mathematics Teacher Educators, Tampa, FL, United States.
Leatham, K.R. (2019). Principles for effectively communicating the theoretical framing of our work. In K. R. Leatham (Ed.), Designing, conducting, and publishing quality research in mathematics education (pp. 169-182). Springer. https://doi.org/10.1007/978-3-030-23505-5_12
Leatham, K. R., & Barton, D. R. (2017). What (research on) technology in the mathematics classroom can and cannot do. In D. A. Spangler & J. J. Wanko (Eds.), Enhancing classroom practice with research behind Principles to Actions (pp. 129-139). National Council of Teachers of Mathematics.
Lee, H. S., & Hollebrands, K. F. (2008). Preparing to teach mathematics with technology: An integrated approach to developing technological pedagogical content knowledge. Contemporary Issues in Technology & Teacher Education, 8(4), 326-341. https://citejournal.org/volume-8/issue-4-08/mathematics/preparing-to-teach-mathematics-with-technology-an-integrated-approach-to-developing-technological-pedagogical-content-knowledge
Lee, H.S., & Hollebrands, K.F. (2011). Characterising and developing teachers’ knowledge for teaching statistics with technology. In C. Batanero, G. Burrill, & C. Reading (Eds.), Teaching statistics in school mathematics – Challenges for teaching and teacher education (pp. 359-369). Springer.
Lester, F. K. (2005). On the theoretical, conceptual, and philosophical foundations for research in mathematics education. ZDM, 37(6), 457-467. https://doi.org/10.1007/BF02655854
Leont’ev, A. N. (1978). Activity, consciousness, and personality. Prentice Hall.
Liang, X., Wang, R., & Bai, G. (2009). A multi-agent system based on activity theory for collaborative network learning. In Z. Hu (Ed.), First International Workshop on Education Technology and Computer Science (Vol. 1, pp. 392-397). IEEE.
Lovett, J.N., McCulloch, A.W., Dick, L., & Cayton, C. (2020). Design principles for examining student practices in a technology-mediated environment. Mathematics Teacher Educator, 8(3), 120-133. https://doi.org/10.5951/MTE.2020.0007
McCulloch, A.W. (2011). Affect and graphing calculator use. Journal of Mathematical Behavior, 30, 166-179. https://doi.org/10.1016/j.jmathb.2011.02.002
McCulloch, A.W., Leatham, K.R., Lovett, J.N., Bailey, N.G. & Reed, S. (2021). How we are preparing secondary mathematics teachers to teach with technology: Findings from a nationwide survey. Journal for Research in Mathematics Education, 52(1), 94-107. https://doi.org/10.5951/jresematheduc-2020-0205
McCulloch, A.W., Hollebrands, K.F., Lee, H.S., Harrison, T., & Mutlu, A. (2018). Factors that influence secondary mathematics teachers’ integration of technology in mathematics lessons. Computers and Education, 123, 26 – 40. https://doi.org/10.1016/j.compedu.2018.04.008
Mishra, P., & Kohler, M. M. (2006). Technological pedagogical content knowledge: A framework for teacher education. Teachers College Record, 108(6), 1017-1054.
Mewborn, D. S. (2005). Framing our work. In G. M. Lloyd, M. Wilson, J. L. M. Wilkins, & S. L. Behm (Eds.), Proceedings of the 27th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. Virginia Tech.
Nardi, B. (Ed.) (1996). Context and consciousness: Activity theory and human-computer interaction. MIT Press.
National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematical success for all. Author.
National Council of Teachers of Mathematics. (2015). Strategic use of technology in teaching and learning mathematics: A position of the National Council of Teachers of Mathematics. https://www.nctm.org/Standards-and-Positions/Position-Statements/Strategic-Use-of-Technology-in-Teaching-and-Learning-Mathematics/
Niess, M. L. (2005). Preparing teachers to teach science and mathematics with technology: Developing a pedagogical content knowledge. Teaching and Teacher Education, 21(5), 509-523. https://doi.org/10.1016/j. tate.2005.03.006
Niess, M. L., Ronau, R. N., Shafer, K. G., Driskell, S. O., Harper, S. R., Johnston, C., Browning, C., Ozgun-Koca, S. A., & Kersaint, G. (2009). Mathematics teacher TPACK standards and development model. Contemporary Issues in Technology and Teacher Education, 9(1), 4-24. https://citejournal.org/volume-9/issue-1-09/mathematics/mathematics-teacher-tpack-standards-and-development-model
Pea, R. D. (1985). Beyond amplification: Using the computer to reorganize mental functioning. Educational psychologist, 20(4), 167-182. https://doi.org/10.1207/s15326985ep2004_2
Puentedura, R. R. (2006). Transformation, technology, and education. http://hippasus.com/resources/tte/
Roblyer, M. D., & Doering, A. H. (2010). Integrating educational technology into teaching (5th ed.). Allyn & Bacon/Pearson.
Shaffer, D. W., & Kaput, J. J. (1998). Mathematics and virtual culture: An evolutionary perspective on technology and mathematics education. Educational Studies in Mathematics, 37(2), 97-119. https://doi.org/10.1023/A:1003590914788
Sherman, M. F. (2014). The role of technology in supporting students’ mathematical thinking: Extending the metaphors of amplifier and reorganizer. Contemporary Issues in Technology and Teacher Education, 14(3), 220-246. https://citejournal.org/volume-14/issue-3-14/mathematics/the-role-of-technology-in-supporting-students-mathematical-thinking-extending-the-metaphors-of-amplifier-and-reorganizer
Sherman, M., & Cayton, C. (2015) Using appropriate tools strategically for instruction. Mathematics Teacher, 109(4), 306–310. https://doi.org/10.5951/mathteacher.109.4.0306
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4-14. https://doi.org/10.3102/0013189X015002004
Sinclair, M. P. (2003). Some implications of the results of a case study for the design of pre-constructed, dynamic geometry sketches and accompanying materials. Educational Studies in Mathematics, 52(3), 289-317. https://doi.org/10.1023/A:1024305603330
Smith, M., & Stein, M. K. (1998). Selecting and creating mathematical tasks. Mathematics Teaching in the Middle School, 3(5), 344–50.
Thomas, A., & Edson, A. J. (2017). A framework for mathematics teachers’ evaluation of digital instructional materials: Integrating mathematics teaching practices with technology use in K-8 classrooms. In P. Resta & S. Smith (Eds.), Proceedings of Society for Information Technology & Teacher Education International Conference (pp. 11-18). Association for the Advancement of Computing in Education (AACE).
Thomas, A., & Edson, A. J. (2019). A framework for teachers’ evaluation of digital instructional materials: Integrating mathematics teaching practices with technology use in K-8 classrooms. Contemporary Issues in Technology and Teacher Education, 19(3), 351-372. https://citejournal.org/volume-19/issue-3-19/mathematics/a-framework-for-teachers-evaluation-of-digital-instructional-materials-integrating-mathematics-teaching-practices-with-technology-use-in-k-8-classrooms
Trocki, A. (2014). Evaluating and writing dynamic geometry tasks. The Mathematics Teacher, 107(9), 701-705. https://doi.org/10.5951/mathteacher.107.9.0701
Trocki, A., & Hollebrands, K. (2018). The development of a framework for assessing dynamic geometry task quality. Digital Experiences in Mathematics Education, 4(2-3), 110-138. https://doi.org/10.1007/s40751-018-0041-8
Vygotsky, L. S. (1978). Mind in society: The development of higher psychological processes. Harvard University Press.
Wilson, P. H., Lee, H. S., & Hollebrands, K. (2011). Understanding prospective mathematics teachers’ processes for making sense of students’ work with technology. Journal for Research in Mathematics Education, 42(1), 39-64. https://doi.org/10.5951/jresematheduc.42.1.0039
Zbiek, R. M., & Hollebrands, K. (2008). A research-informed view of the process of incorporating mathematics technology into classroom practice by in-service and prospective teachers. In K. Heid & G. W. Blume (Eds.), Research on technology and the teaching and learning mathematics: Syntheses, cases, and perspectives (Vol. 1, pp. 287–344). National Council of Teachers of Mathematics.
![]()