The unilateral view that teachers are the sole transmitters of knowledge to their students has been challenged by constructivist philosophies and research supporting ambitious instruction (Cobb & Jackson, 2011; Lampert et al., 2010; Lampert & Graziani, 2009). Ambitious instruction involves a collaboration between teacher and students in which student ideas are built upon to ensure successful learning (Lampert et al., 2010). Ambitious teaching practices include selection of high-quality tasks, connections among ideas, and eliciting and responding to student thinking. Unfortunately, most mathematics classroom interactions are not characterized by the aspects of ambitious teaching and, instead, are teacher-centered with limited opportunities for students to share their thinking (Michaels & O’Connor, 2015).
One of the first steps to engage in ambitious teaching is to bring student thinking to the center of instruction through eliciting and responding to student ideas (Teaching Works, 2011). As a result, teacher preparation programs have engaged in a more practice-based approach and have developed methods and structures necessary for successfully engaging teacher candidates (TCs) in the complexities of eliciting and responding to student thinking (Kazemi et al., 2009; Lampert et al., 2010; Thompson et al., 2013).
This work within practice-based teacher education provides a context for TCs to have authentic opportunities to practice defined teaching episodes. Rehearsal is one specific aspect of practice-based teacher education that involves peers acting as students as the TC facilitates an activity. Rehearsals allow for concentrated feedback from a teacher educator on specific components of ambitious teaching. An essential component of rehearsals is the discussion that takes place before, during, and after the teaching episode with peers but, more specifically, with the teacher educator.
One way to help teacher educators facilitate rehearsals is to use an innovative technology such as a virtual simulation software. One virtual simulation software available from Mursion® (developed as TLE TeachLivE™) allows simulations of various classroom scenarios for TCs to practice interactions with students (Dieker, Rodriquez et al., 2014). During each virtual simulation, TCs engage with a small group of avatars through interacting with a large computer screen. The student avatars are controlled by a simulation specialist that uses a simulation scenario developed by the teacher educator to guide the instruction and levels of interactions.
In this article, we describe the utilization of a virtual rehearsal simulation (VRS) within a mathematics methods course to develop TCs’ facilitation of effective elicitation skills. This use of virtual simulations provides an innovative context to compare with the current traditional rehearsal that utilizes peers acting as students. Furthermore, the majority of mathematics education research on rehearsals has focused on feedback and procedure (Averill et al., 2016; Kazemi et al., 2016), but this work adds to current literature by analyzing enacted teaching practices.
Knowing how rehearsals impact actual teaching practice to inform use and future development of rehearsals is important to the field. This work brings together unique contexts and outcomes and comparatively examines TCs’ development of elicitation skills in traditional rehearsals and VRSs.
Related Literature
Practice-Based Teacher Education
One criticism of teacher preparation programs has been the lack of balance between theory and practice (Ball & Forzani, 2009; Cochran-Smith & Lytle, 2001; Darling-Hammond, 2006, 2012; Grossman et al., 2009). Shifts in teacher education have prioritized activities that allow TCs to analyze and engage in the act of ambitious teaching early and more frequently in their preparation (Lampert et al., 2010). Research frames opportunities for practice-based preparation as “pedagogies of practice in professional education” (Grossman et al., 2009; Tyminski et al., 2014), which include representations, decompositions, and approximations of teaching practice. At the center of the pedagogies of practice are “high-leverage practices that can be articulated, studied, and rehearsed” (Ball et al., 2009, p. 1039), and eliciting student thinking is one of these key practices.
Eliciting Student Thinking
Learning is a social endeavor, and students from an early age need opportunities to discuss their mathematical thinking in ways that position them as competent (Bartell et al., 2017). When teachers engage in ambitious teaching, they elicit student thinking and use student ideas to inform the mathematical conversation, and as a result, teachers help develop students’ mathematical identities (Smith & Stein, 1998).
Eliciting is a “high-leverage practice” that assesses student understanding and is necessary in avoiding assumptions about students’ abilities (Teaching Works, 2011). The skill of eliciting and responding to student thinking is multifaceted and difficult but can be developed through opportunities of practice and analysis.
Eliciting student thinking requires the teacher to prompt and ask questions of students that reveal their ideas about a mathematical concept. These prompts or questions can result in short, closed-ended responses or can promote students to elaborate their thinking in ways that provide clearer windows into their understanding. Teachers hold the power in eliciting student thinking. Teachers often elicit students’ processes for a mathematics problem (Shaughnessy & Boerst, 2017), but other questioning skills are needed to extend past processes and make connections and support conceptual understanding. One way to help TCs develop eliciting skills is through opportunities to engage in the act of teaching and analyze the result of different questioning techniques.
While the field of mathematics education includes literature on the importance of eliciting student thinking (i.e., Michaels & O’Connor, 2015; Parrish, 2011) research is limited that analyzes the specific development of eliciting skills through different contexts. In the field of science education, one study by Levin et al. (2009) presented findings that a series of video analyses led to improvements in attending to and eliciting student thinking with face-to-face student interactions for most of the participants in a science methods course. Other work in science education revealed that five of seven secondary science education TCs shifted from the initiate, respond, evaluate format (Cazden & Beck, 2003; Mehan, 1979) to asking follow-up or probing questions over the course of one semester with video analysis scaffolding (Gotwals & Birmingham, 2016).
These works in science education provide evidence that elicitation practices of TCs can be influenced by video studies of teaching. That is, as TCs analyze the practices of others they are able to take on elicitation components in their own teaching. An extension of this work is needed to consider how TCs implement elicitation skills through rehearsals and analysis of their own teaching. Such considerations about the structures used in the development of elicitation skills (i.e., peer-to-peer vs. VRS) will aid teacher educators in defining best practices for method courses.
Talk and Teacher Moves
When developing eliciting skills, it is advantageous to not only consider cognitive processes (Anderson et al., 2001), but to also consider how questions and/or prompts position students within the conversation (Correnti et al., 2015). In the mathematics education field scholars have conceptualized eliciting prompts to embody social cognitive theories (Chapin et al., 2009; Correnti et al., 2015; Michaels & O’Conner, 2015; Parrish, 2011). One highly cited resource is that of Chapin et al. (2009), who categorized eliciting strategies as talk moves.Each talk move, described in Table 1, serves a unique role in bringing students into the class discussion.
Table 1 Talk Moves
For example, restating is used to foster active listening to others’ ideas while prompt for further participation is intended to extend a student’s contribution to the discussion. With clear definitions and targeted goals, talk moves are accessible to preservice teachers as a pedagogical tool to help them understand the role and impact of their eliciting prompts.
Another framework, The Analyzing Teacher Moves (ATM) Framework (Correnti et al., 2015), provides a different lens for analyzing how teachers guide discussions. While Chapin’s talk moves categorize elicitation prompts based on the goals for the discussion, the ATM categorizes each utterance a teacher makes with the goal of illuminating patterns in the teacher’s uses of each student’s ideas in their discussions. Each teacher utterance is categorized as teacher moves.
The utterance is categorized by considering the previous student response and the way the teacher is taking up student ideas (Correnti et al., 2015; Scherrer & Stein, 2013). When coding a teacher utterance, therefore, the coder must consider the prior student response, as shown with the italicized text in Table 2, before determining the categorization of the code. The ATM is a targeted method for studying teacher interactions and positioning students in more active or passive roles (Scherrer & Stein, 2013). Each teacher move is broadly categorized as initiating moves (e.g., launch and literal), which are moves a teacher uses to start a discussion of a set problem/topic, and rejoiner moves (e.g., uptake and connection), which are moves that show a teacher is hearing what a student has said and continuing the discussion with student ideas at the forefront. Table 2 provides a description of each code along with an example of the move within a mathematics context.
Table 2 Categorization of Teacher Discourse Moves
| Initiating Moves | Rejoiner Moves |
|---|---|
| Launch An open-ended question at the beginning of a lesson (or a segment of a lesson) meant to invite student thinking. How did you solve this problem? | Repeats Teacher echoes student response It would be 10. So, you got 10. |
| Literal Question asks for the retrieval of factual information. The teacher often is looking for a specific answer. What is 3 x 4? | Uptake Teacher uses a student response to extend, deepen, clarify, or elaborate the discussion. This includes asking a student to restate another student’s idea. It is like a pattern. Explain the pattern you see? I added three groups of 15 to get 45 and then doubled that. Danni can you share in your own words how Skylar just solved this problem? |
| Think aloud When the teacher talks about how s/he is thinking about a passage or a problem. So, when I take 12 times 4, I break it down into 12 time 2 and then double that. | Uptake-Literal Teacher asks a literal question using a student response. I did 2 groups of 3. What is 2 x 3? |
| Provides information Teacher gives information (answer or method) related to the instructional task at hand. Teacher reviews or reveals relevant information from prior text or provides information relevant to the task at hand. When you break 25 into 20 and 5, this is called decomposition. | Push-Back A type of uptake in which teacher challenges the response in order to encourage students to rethink or defend their responses. I made the 9 and 10 to make is easier. Will that always work? |
| Collecting Teacher attempts to gather additional responses to a question. I added 3 and 3 to get 6. Did anyone solve a different way? | |
| Connection Teacher tries to get students to make an explicit connection. Well, I thought of this problem as repeated addition. How is your way of solving similar to the way Raya just solved? |
Talk moves are a broader categorization of the elicitation of student thinking, while the ATM provides a finer grain to examine the nature of their eliciting strategies. For example, when a teacher chooses to “prompt for further participation,” one of the talk moves, it could take many different forms. For a novice, the initial goal is to prompt a student for more information, and once that move is more routine, it can be further stretched and deepened.
One move to prompt further participation might be to ask, “What did you get?” in a series of closed-ended, literal questions as classified by teacher moves. Another move might be to prompt “Tell me more about how you thought about that?” which is more open-ended and student led and classified as an uptake move within the teacher moves.
These two forms of eliciting are different and require a finer grained coding process to distinguish the difference. Table 3 overlays the talk moves as described in Chapin et al. (2009) with the ATM framework (Correnti et al., 2015) to show the ways the frameworks align and diverge from each other. This overlay shows that the ATM framework further delineates certain talk moves, such as revoicing and prompt for further participation. For example, a series of utterances that are categorized as revoicing by talk moves will be coded as repeat and uptake literal, based on the specific way the teacher used the student’s idea. At the same time, certain talk moves, such as apply reasoning of another, are matched to the ATM framework code of connection.
Table 3 Connection Between Talk Moves and ATM Teacher Moves
| Talk Moves | Example of What the Teacher Might Say (ATM Teacher Moves) |
|---|---|
| Wait time Allowing time after a question is asked before soliciting a response | N/A |
| Revoice The teacher rephrases a student’s response to clarify or highlight | So, you decomposed the 15 into 10 and 5. Is that what you did? (Repeat; Uptake Literal) |
| Restate Another student shares a fellow student’s idea or strategy in their own words | Who can share what Sahra just said in their own words? (Uptake) |
| Prompt for further participation Elicit additional information about student thinking | What did you do next? (Uptake-Literal) Tell me more about how you solved this? (Uptake) Will this strategy always work? (Pushback) How is this strategy similar to how we have been breaking apart numbers by place value? (Connection) |
| Apply reasoning of another | Do you agree with Jordyn and why? (Connection) |
| Turn and Talk | What do you think of Sami’s idea? (Uptake) Turn and talk with your neighbor. |
The strategic use of eliciting strategies, whether they are categorized as talk moves or teacher moves, is essential for the development of ambitious teaching for preservice teachers. The practice of these eliciting strategies and examination of their impact are key components of teacher education programs that prioritize the act of teaching.
Rehearsals
One of the key pedagogies of practice-based teacher education used to develop eliciting skills in TCs is the use of rehearsals to approximate classroom instruction. Rehearsals are one part of an iterative sequence known as Cycles of Enactment and Investigation(Kazemi et al., 2016; Lampert et al., 2013) that involves observation, analysis, rehearsal, and enactment. In the rehearsal, TCs take on the role of the teacher and lead an instructional activity. During this short lesson, the instructor is able to mediate the experience in real-time through the use of brief time outs to capitalize on teachable moments (for more on time outs, see Wæge & Fauskanger, 2020).
The instructor then debriefs with the TC to provide feedback and refine the plan. The TC implements the same instructional activity in a classroom setting. The iterative nature of using the same instructional activity allows TCs to focus on their use of targeted ambitious teaching practices, such as eliciting student thinking. In this sense, rehearsals differ from other teaching models such as microteaching, which often is more like a full lesson taught to peers. The rehearsal is more binded in the task used (e.g., number routine, and coral counting) to allow for the focus on selected high-leverage practices (Lampert & Graziani, 2009).
Rehearsals documented in the literature utilize a peer-to-peer context in which the TC leads the instructional activity with a small group of their peers from the course who are role playing as students (Anthony et al., 2015; Kazemi et al., 2016). The instructor takes on a dual role of coach and also serves as a student by contributing responses for the TC to consider.
Work in the field has documented the planning processes of the instructors (Kazemi et al., 2009), investigated the role of the teacher educator within the rehearsal (Kazemi et al., 2016), and examined TC noticing practices (Anthony et al., 2015). These examples from the literature explored face-to-face contexts and the use of the peer-to-peer model, but little is known about how rehearsals could be used in other contexts, such as online platforms or other virtual environments.
Innovative technologies open space for rehearsals to be performed in other contexts. Technologies such as virtual simulations take on characteristics of the classroom setting through the use of avatars and simulated environments. Virtual simulation software, such as that available from Mursion® (developed as TLE TeachLivE™), provides immersive, interactive learning of high-leverage practices through practice-based teacher development (Dieker, Straub, et al., 2014; O’Callaghan & Piro, 2016). Use of virtual simulations shows promise for better preparing educators to facilitate 21st-century learning and transferable skill acquisition, such as eliciting student thinking to better inspire and prepare K-12 students (Bousfield et al., 2016). Research demonstrates that virtual simulations provide TCs with a unique opportunity for practice with complex communication skills, which is difficult to replicate with typical fieldwork (Straub, Dieker, Hughes, et al., 2014).
This study situated the research of rehearsals within the virtual simulation context, therefore, adding to the field by analyzing the possibility of merging these lines of work. By comparing outcomes of traditional rehearsals within virtual simulation rehearsals, this work took the initial steps to better understand the affordances and hinderances of innovative approaches. Furthermore, this work documented how virtual simulations assisted teacher educator preparation programs in the explicit training of TCs in selected teaching practices.
Virtual Simulations in Teacher Preparation Programs
Teacher educators are challenged in providing TCs with meaningful and authentic spaces to practice essential pedagogical tools and management skills of a classroom (Prett-Frontczak et al., 2005). Traditionally, teacher educators have commonly used role-playing with peers within college classrooms, also known as rehearsals or microteaching, to train and prepare TCs for the real classroom practice in the form of field experiences. Field experiences are crucial to providing TCs with opportunities to interact with students, classroom teachers, and other TCs in a live setting.
Within a field experience, TCs are able to observe and experience the range of complex situations that arise in actual classrooms, illustrating for them the conceptual understanding needed to be a successful teacher (Clift & Brady, 2005). The complexity of teaching can be overwhelming for a TC if the TC is not adequately prepared for the cognitive demands of a field experience (Hixon & So, 2009). When TCs feel unprepared, they may also feel unsuccessful in their teaching abilities during their practice in the field experience. In this case, the field experience becomes a negative event instead of a valuable learning experience in their growth as teachers. As such, teacher educators must provide TCs with deliberate opportunities to practice teaching methods, attempt new strategies, and most importantly, receive purposeful feedback on their teaching practices.
As an effort to provide TCs with extensive and advanced hands-on preparation prior to entering a real classroom, teacher educators continue to explore innovative new ways to use technology in teacher preparation (Boggs et al., 2007). Virtual simulations using a multimedia platform such as TLE TeachLivE or Mursion are immersive, mixed reality classroom simulators that utilize common teaching materials such as whiteboards, classroom desks, and student avatars (Dieker et al., 2008).
When using a virtual simulation learning environment, a teacher educator can combine learning content knowledge and teaching pedagogy with immediate feedback and discussing problem-solving strategies (Ayres, 2008; Rieg & Wilson, 2009). The virtual simulation learning environment merges the real and virtual worlds, offering users a sense of presence and realness in the virtual environment. TCs often state that they felt the virtual simulation environment resembled a real classroom (Kaufman & Ireland, 2016; Lee et al., 2018). These environments are offering teacher preparation programs with an alternative pedagogical tool for training teachers and have been recognized as effective and efficient approaches (Straub, Dieker, Hughes et al., 2014).
Virtual simulation environments were developed to represent a variety of students’ academic and behavioral ranges that exist in real classrooms (Dieker et al., 2008; Dieker, Rodriguez et al., 2014). The Mursion simulation environment provides teacher educators the ability and autonomy to create individualized and realistic experiences for TCs to practice specific pedagogical skills.
When planning a session, teacher educators can create distinctive scenarios specialized in content and can include specific student-avatar behaviors or responses that will require TCs to react immediately and adapt in the simulation. For example, a teacher educator can write a scenario that will include a student-avatar expressing confusion to a task. This response will require the TC to attend to this student in the moment within the simulation. After the session, the teacher educator and TCs are able to reflect about the teaching practices exhibited, and studies have shown that this immediate feedback is beneficial to TC development (Peterson-Ahmad et al., 2018).
The use of simulations in teacher preparation programs is being explored more to provide TCs with the opportunity to practice on content-specific lesson planning and implementation, classroom management, and teaching students with a range of learning needs and challenges (Bradley & Kendall, 2014; Girod & Girod, 2008). In the field of special education, Dawson and Lignugaris/Kraft (2017) investigated the development of four preservice teachers’ skills specific to praise and error correction in language development through the use of virtual simulations. They found improvement in target skills when practicing in the virtual simulation, but mixed results when facilitating lessons in a classroom setting.
Straub, Dieker, Hynes et al. (2014) offered preliminary results of several research studies investigating the use of the TLE simulator in teacher educator programs that illustrated encouraging outcomes. These studies included TCs practicing with revising mathematics lesson plans, rehearsing read-alouds, managing student behaviors, and attempting to use various questioning techniques.
The studies did not include specific metrics to examine development of elicitation skills in mathematics teaching practice for preservice teachers; however, one study by Dieker et al. (2017) examined development of eliciting skills for in-service teachers who participated in professional development with or without virtual simulation opportunities. Their work found that in-service teachers with opportunities to practice in virtual environments increased their frequency of prompts for student explanation in their classroom discussions. In-service teachers who received only the professional development component decreased in their use of explanation prompts. The impact of simulation experiences on enacted practices requires more attention because the enactment in the classroom is where students reap the benefits. Furthermore, by studying the impact of simulation experiences on TCs’ enacted practices, teacher education programs will gain insight into ways to develop skills early and impact even more students.
This current study sought to extend research to examine the development of elicitation skills with novice teachers in peer-to-peer and virtual simulation rehearsals. The study addressed the following research questions:
- How do TCs who engage in either peer-to-peer or VRS compare in their development of elicitation skills within the rehearsal episodes?
- How do TCs who engage in either peer-to-peer or VRS compare in their application of elicitation skills in authentic teaching contexts?
Methods
This study focused on one part of a larger project (Project INTERSECT) that created STEM VRS scenarios to expand practice-based teaching education (Grossman et. al, 2009) and attended to the specific needs of mathematics and science teacher development. This longitudinal project examined whether integration of VRS into mathematics and science education courses improves TC performance with eliciting skills.
Participants and Setting
For this particular study, the participants were 60 TCs enrolled in two sections of a Grades 3-6 Mathematics Methods course at a university teacher-preparation program in the southeastern United States. TCs were assigned to sections based on their cohort to allow them to take classes together and build community. These cohorts were randomly assigned.
The control group consisted of 22 TCs who led two number talks within peer-to-peer rehearsals (i.e., Rehearsal 1 and Rehearsal 2) and then led one number talk within the elementary classroom in which they were completing their practicum (i.e., Classroom Enactment). In the comparison group, 38 TCs led two number talks within the virtual simulation (i.e., Rehearsal 1 and Rehearsal 2) and then led one number talk within their practicum experience (i.e., Classroom Enactment). For both control and comparison each event occurred approximately 2 weeks apart.
Each peer-to-peer and simulation session (three to four TCs per session) was recorded and segmented based on individual sections for which the TC was in the teacher role. Each TC then reviewed and analyzed their segment within a course assignment. Each recording segment was transcribed, which resulted in three teaching episodes transcribed per participant; a total of 180 transcripts were used for data analysis.
Prior to involvement in the study, participants successfully completed a mathematics content course for elementary teachers and a mathematics methods course focused on the primary grades (K-2). The prerequisite content and methods courses did not involve rehearsals. As a part of this study, participants were enrolled in a mathematics course focused on upper elementary grades (3-6), which included an integrated practicum.
The Grades 3-6 mathematics methods course concentrated on the development of multiplicative reasoning, specifically single-digit and multidigit multiplication and division, fraction concepts, and fraction operations. The pedagogical foci of the course are a continuation of eliciting student thinking from the primary grades methods course and facilitating whole group mathematical discussions. All sections of the Grades 3-6 mathematics methods course in the study had the same instructor, who was a lead researcher on this study. Course components were enacted with consistent progression, and uniform assignments were utilized for each section.
In the mathematics methods course, teacher moves were modeled and discussed in terms of how certain teacher questions and comments guided a mathematical discussion to be more student-centered instead of unidirectional (Michaels & O’Connor, 2015). In the first week of instruction, TCs were introduced to talk moves (Chapin et al., 2009), and lesson recordings were analyzed based on talk moves. The talk move framework was selected over the ATM framework as tool for TCs due to accessibility of the talk moves. The broader categorization of teacher prompts allowed TCs to consider their role within the discussions without being overwhelmed by individual utterances that are the unit of analysis with the ATM.
Each week, the instructor led TCs in an instructional activity, number talks—with the TCs as participants. Number talks (Parrish, 2010) are short, 7- to 10-minute mathematical routines, in which participants solve a computational problem and the instructor guides a discussion of solution strategies. During and after each instructor-led number talk, the instructor led a discussion decomposing the talk moves used, impact of the moves, representation of the mathematics used on the white board, and key multiplicative reasoning concepts. During the semester, TCs facilitated two number talks as a part of a rehearsal cycle (peer-to-peer or VRS). TCs analyzed their own number talks similarly to the instructor’s process, using prompts regarding talk moves, impact of moves, representations, and multiplicative reasoning.
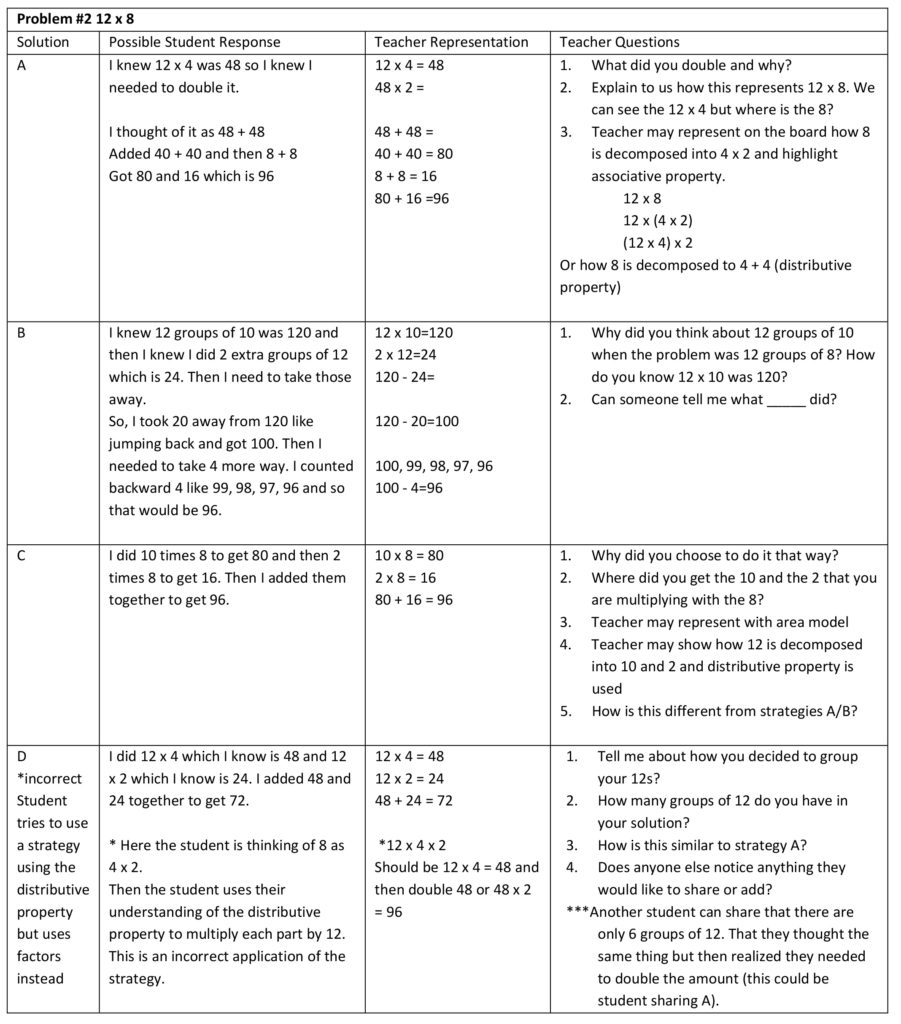
For both number talk rehearsals, groups of three or four TCs led a string of number talks with multidigit multiplication problems that were sequenced to build on each other. For example, the first number talk rehearsal problems (12 × 4, 12 × 8, 12 × 15, and 12 × 24) were used as a purposeful number string. That is, the first TC would lead a number talk with 12 × 4 as the other TCs role played as students. Then, the second TC would lead a number talk with 12 × 8 as the other TCs were the students.
For the second number talk, rehearsal problems 35 × 4, 35 × 6, 35 × 8, and 35 × 16 were used as the number string. During each rehearsal, the instructor provided feedback and coaching within the session. At times, this allowed for timeouts, as detailed in Lampert et al. (2013), during which the peers would pause or the simulated students would go away on the screen.
At the end of each group session, the instructor led a debrief session with the group members focused on talk moves, mathematical representations, multiplicative reasoning, and positioning of students. After completing two rehearsals, each participant enacted a number talk in a third-, fourth-, or fifth-grade classroom. The differences between the control and comparison group will be further delineated in the following sections.
Control Group: Peer-to-Peer Rehearsal
In the peer-to-peer rehearsal, three or four TCs were grouped together. As one TC led the number talk, the other three or four TCs played the role of students, as in a traditional rehearsal. All TCs collaboratively planned for the number talk string of problems and anticipated student solution methods. These anticipated strategies were the same strategies used within the simulation scenarios. When role playing as the students, the TCs selected an anticipated student solution method to share. These were not assigned but aligned with the strategies used in the VRS. The TC acting as the teacher had access to a whiteboard to record student thinking. During the rehearsal, the instructor provided coaching and time outs when appropriate.
The instructor also played the role of a student to present alternative solution methods if needed. After each rehearsal, the instructor led a debrief particular to that TC. When all group members completed their number talk rehearsal, the instructor led an additional debrief on the overall learnings. The peer-to-peer rehearsal sessions took place during a class session time frame. Each group came at an assigned time, and TCs completed other activities during the time they were not engaged in their rehearsal. This strategy allowed the instructor to be present in all rehearsal sessions.
Comparison Group: Virtual Simulation Rehearsal
In the VRS, three or four TCs were grouped together for each session. The sessions took place in the virtual simulation lab that was set up like an elementary classroom. The avatar students were on a TV screen that was sized to allow the avatars to take on a more realistic position in a classroom setting (see Figure 1). The avatar students were seated around a kidney-shaped table on the screen. As one TC led the VRS, the other two or three TCs observed without participating. They were present in the room but not seen by the avatars. TCs had access to a whiteboard to represent student solutions, and as shown in Figure 2, the TC and avatars were captured in the video recording process.
Figure 1 Simulation Room Setup

Figure 2 Example of Components Captured in the Video Recording

The simulation operator was an actor by trade who was trained by Mursion. The extensive training through Mursion equipped the simulation operator to approximate the personalities and behaviors of five avatar students while manipulating a system that controlled their voices and body movements. The same simulation operator led each VRS and worked collaboratively with the instructor of the course. The simulation operator met with the instructor two times to review and practice each of the two scenarios prior to the start of a series of sessions. The instructor and simulation operator also met briefly prior to each individual session to double check technology and discuss any questions.
The scenario (Figure 3) detailed student responses to the multiplication problems based on solution strategies that are well-documented in the mathematics education research (Carpenter et al., 2016). The simulation operator assigned a student avatar to each solution strategy and then provided responses during the VRS that aligned with this way of solving. Anticipated questions were provided and discussed during the meetings to ensure the simulation operator felt comfortable with responses. The simulation operator was prepared for questions that connected different students’ responses and attended to other student solution methods.
Figure 3 Excerpt From Simulation Scenario
During the rehearsal, the instructor provided coaching and time outs by saying, “Pause simulation,” to offer feedback. After each rehearsal, the simulation was paused while the instruction led a debrief particular to that TC. When all group members completed their VRS, the instructor led an additional debrief on the overall learnings. Same as the peer-to-peer rehearsal sessions, each VRS session took place during a class session time frame. Each group came at an assigned time, and TCs completed other activities during the time they were not engaged in their rehearsal. This approach allowed the instructor to be present in all rehearsal sessions.
Analysis
Each of the 180 transcripts was coded using the Analyzing Teacher Moves (ATM) framework (Stein et al., 2013) to examine the type of teacher moves used in each teaching episode. Frequency counts of teacher moves (Table 2) were used in this study to compare the peer-to-peer and VRS groups quantitatively in their development of certain eliciting strategies.
Reliability
Two members of the research team were trained on the ATM framework, to employ collaborative coding (Saldana, 2016) due to the quantity of data. The teacher moves from the ATM framework were used as a set of a priori codes, and transcripts were coded to document the use of each teacher move.
The transcripts were coded with a teacher turn as the unit of comparison. A teacher turn is defined as the segment of teacher utterances (e.g., questions, prompts, or information) separated by student contributions. In a conversation the point at which one person stops talking and another begins indicates a turn in the conversation. Codes were compared within the teacher turn, and agreement was counted if codes matched in the turn. A subset of 10 transcripts from a previous research project were double coded and used to train and discuss codes. A subsequent set of five transcripts were double coded, and teacher turns that were coded with different moves were discussed. Descriptions of teacher moves were directly referenced, and the two researchers reached 100% consensus on the coded moves.
The key phrases and questions were noted and indexed with the agreed codes to provide a reference for future coding. Another set of five transcripts was coded, and the 80% reliability goal was reached. Lead researchers set 80% as the goal based on literature-derived recommendations (Bernard, 2011; Boyatzis, 1998; DeCuir-Gunby et al., 2011; Hruschka et al., 2004; Krippendorff, 2009; Saldana, 2016), despite some calls for “dispensing with such quantitative measures altogether” (Saldana, 2016, p. 37). Next, groups of 20 transcriptions were coded individually, with a common transcript coded as a drift check (Syed & Nelson, 2015). This process supported the efficient coding of large data sets, but also helped ensure effective, reliable application of codes.
Quantitative Analysis of Frequencies
This study was an initial examination of the development of eliciting skills in VRS and peer-to-peer rehearsals. The frequency of the qualitative codes was calculated in 5-minute intervals as an initial measure to compare. Five-minute intervals were used as a method of norming so that frequency counts from different length teaching episodes could be compared accurately (as recommended by Biber et al., 1998). That is, reporting that the average use of a move was one meant that the move was used, on average, one time per 5-minute interval.
The change in normed frequency counts were then compared between comparison group (VRS) and control group (peer-to-peer) at corresponding time points – Rehearsal 1 to Rehearsal 2, and Rehearsal 1 to Enactment. For each individual code, the data were visualized using side-by-side boxplots for the differences between the time points (value at Rehearsal 2 minus value at Rehearsal 1). This visualization of the data allowed for outliers and ranges to be considered. For each code, the differences were summarized using means, the number of missing values, the number of zero values, and the summaries associated with the boxplot. Raw data (before taking differences) were visualized to check for interesting features that would not be found using the differences alone; none were found.
Statistical inference for comparing the two groups was carried out using the (nonpooled) two-sample t-test along with the associated 95% confidence interval. For codes with extreme outliers or other problems revealed by the plots, the groups were also compared using Fisher’s exact test for the 2 by 2 table. For each code, two tables were considered: one where the rows correspond to increase and not increase and the other where the rows correspond to not decrease and decrease.
Results
The moves examined in this study were categorized based on the way the teacher positioned the students’ ideas. More Uptake, Connection, and Pushback moves depict a discussion in which the teacher asked students to use and respond to student-shared ideas and not just univocally answering questions posed by the teacher. Series of Literalmoves represent a discussion in which the teacher was not using the student’s ideas, but instead asking for responses to teacher-generated prompts. The Uptake-Literal move is an in-between; it shows that a teacher was using the student’s idea but asking a follow-up question that required only a direct, short answer. Other moves, Provides Information, Repeat, and Think Aloud, signified the teacher was communicating ideas to students. The results of the comparative analyses between peer-to-peer and VRS are presented as they relate to the research questions.
Research Question 1
The differences in the means of frequencies between Rehearsal 1 and Rehearsal 2 for each move (Table 4) shows that both control and comparison groups increased in their use ofLaunch and Connection moves and decreased in their use of Uptake and Pushback moves. The average use of Literal and Provides Information moves did not change much between rehearsals, as noted by the mean change of almost zero for both. For Uptake-Literal and Think Aloud, the control group members decreased in their average use of the moves while the comparison group increased use.
Table 4 Change in Averages from Rehearsal 1 to Rehearsal 2
| Moves | Control Mean (SD) | Comparison Mean (SD) | 95% CI for Difference in Means | t |
|---|---|---|---|---|
| Launch | 0.12 (0.48) | 0.02 (0.55) | -0.23, 0.43 | 0.61 |
| Uptake | -0.21 (2.30) | -0.15 (2.94) | -1.74, 1.64 | -0.06 |
| Pushback | -0.49 (1.06) | -0.22 (1.53) | -1.11, 0.58 | -0.64 |
| Connection | 0.44 (0.81) | 0.24 (0.48) | -0.23, 0.62 | 0.93 |
| Literal | 0.09 (0.30) | -0.08 (0.94) | -0.28, 0.64 | 0.80 |
| Uptake-Literal | -0.93 (2.00) | 1.04 (2.93) | -3.58, -0.36 | -2.48* |
| Repeat | 0.72 (2.01) | -0.02 (1.98) | -0.54, 2.01 | 1.16 |
| Provides Information | 0.00 (2.26) | 0.04 (1.23) | -1.21, 1.13 | -0.07 |
| Think Aloud | -0.34 (0.63) | 0.17 (0.34) | -0.79, -0.14 | -2.90 |
| *p < .05 | ||||
When comparing the groups in terms of differences between Rehearsal 1 and Rehearsal 2, the use of Uptake Literal was statistically significant with a larger mean difference for the comparison group (p = 0.02). Fisher’s exact test also showed the groups differed when compared using Uptake Literal(p = 0.03). Between the first two timepoints, the comparison group increased in the average use of Uptake-Literal moves by one move per minute, while the control group decreased in their average use of this move by one move per minute.
Research Question 2
From Rehearsal 1 to Classroom Enactment, both groups increased in average use of all moves except for Think Aloud, for which the control group decreased in their use (Table 5). These statements describe the data as observed and do not indicate statistically significant increases or decreases.
Table 5 Change in Averages From Rehearsal 1 to Classroom Enactment
| Control Mean (SD) | Comparison Mean (SD) | 95% CI for Difference in Means | t | |
|---|---|---|---|---|
| Launch | 0.66 (1.20) | 1.05 (1.46) | -1.20, 0.44 | -0.94 |
| Uptake | 1.16 (2.68) | 0.51 (3.42) | -1.22, 2.52 | 0.70 |
| Pushback | 0.66 (1.75) | 0.16 (1.81) | -0.62, 1.61 | 0.90 |
| Connection | 0.70 (1.16) | 0.17 (0.95) | -0.16, 1.21 | 1.57 |
| Literal | 0.58 (1.20) | 0.45 (1.22) | -0.62, 0.90 | 0.38 |
| Uptake-Literal | 4.11 (3.35) | 1.52 (4.99) | 0.05, 5.13 | 2.06* |
| Repeat | 4.21 (4.77) | 1.13 (3.69) | 0.30, 5.86 | 2.27* |
| Provides Information | 0.59 (1.80) | 1.17 (2.97) | -2.04, 0.86 | -0.81 |
| Think Aloud | -0.31 (0.77) | 0.01 (0.25) | -0.73, 0.08 | -1.69 |
| *p < .05 | ||||
Statistical comparison showed that the mean difference in use of the Uptake Literal move was significant when comparing Rehearsal 1 to Classroom Enactment, with the larger mean difference for the control group (p = 0.05). The control group increased in their use of Uptake-Literal by an average of four moves per 5-minute interval, while the comparison group increased an average of 1.5 moves per interval. For the control group, all but one participant increased for Uptake Literal. For the code Repeat, all participants increased in the control group, which this was different from the comparison group (p = 0.03). The control group increased in their use of Repeat by an average of four moves per 5-minute interval, and the comparison group increased an average of one move per 5 minutes.
Discussion
This study of VRS is a preliminary step in comparing how TCs develop eliciting skills for mathematical discussions within different instructional contexts (i.e., peer-to-peer or virtual simulation). The results show increases and decreases in average frequency counts of certain elicitation moves across time and context, which shed light on differences between contexts. The findings and direct implications are discussed in relation to the research questions.
Research Question 1
In response to the first research question, descriptive and inferential statistics provide a picture of how TCs develop elicitation skills over time in different contexts. On average, both groups decreased in their use of Uptake and Pushback moves from Rehearsal 1 to 2. This decrease means that TCs were using fewer open-ended questions that were probing student thinking. This descriptive finding is counter to research by Dieker et al. (2017), which found that in-service teachers increased their use of explanation questions (Uptake and Pushback are explanation moves) over each simulation session. This difference between in-service and TCs reveals differences in how experience might impact development of questioning skills.
A promising trend between rehearsals is that both groups increased in their use of the Connectionmove, which means TCs were prompting participants to share connections between strategies. Allowing space for students to make these connections is an essential element of ambitious teaching, in that teachers use students’ strategies to build conceptual understanding (Lampert et al., 2010). The instructional activity used in the rehearsal was a number talk (Parrish, 2010), and the nature of this activity is to elicit multiple students’ solution methods to one computational problem. Across time, in both peer-to-peer rehearsals and VRS, TCs seem to be providing more opportunities for students to make connections between strategies, and for teacher educators this finding supports use of number talks to build these elicitation skills.
The sole statistically significant difference between groups was that the comparison group using the VRS increased in their use of Uptake-Literal from Rehearsals 1 to Rehearsal 2, while participants in peer-to-peer rehearsals decreased in their use of the Uptake-Literal move. While using an Uptake-Literal move does utilize a students’ response, the question requires only a recall answer, such as “Where is the 5 from?” This differential use of more literal questioning is also coupled with a decrease in Uptake and Pushback for both groups from Rehearsal 1 to Rehearsal 2.
The observation of an increase in the use of Uptake-Literalmove among the comparison group and decrease in Uptake and Pushbackmoves across both groups may suggest that TCs in the VRS positioned students to answer more literal questions in their second rehearsal than in their first rehearsal. This increase in the VRS context is interesting and requires further investigation to understand the nature of this increase.
In terms of the peer-to-peer rehearsals, Bell (2007) reported that peers were likely to provide more elaborate descriptions of their thinking, and therefore, the teacher would not have to ask as many follow-up questions. This finding aligns with the decrease in Uptake-Literal moves for the peer-to-peer context, in that participants did not ask as many questions, such as “What did you do next?” or “Where is the 12 represented?” TCs in the comparison group worked with avatar-students who may not have been as forthcoming in their descriptions, therefore prompting more questioning of this nature.
Research Question 2
Regarding the second research question, this study compared how TCs utilized elicitation prompts in authentic classroom settings by comparing how they changed in their average use of moves from their first rehearsal to classroom lesson. From Rehearsal 1 to Classroom Enactment TCs increased in the more explanation-centered moves; that is, TCs who engaged in peer-to-peer rehearsals and VRS increased similarly in their use of these moves. This finding, again, was counter to findings by Dieker et al. (2017), in that teachers who engaged in virtual simulations utilized significantly more explanation question types than did the control group. These differences in development warrant further investigation to better understand how eliciting skills are incorporated into a novice teachers’ repertoire to lead classroom discussions.
The use of Uptake- Literal shifted when examining Rehearsal 1 to Classroom Enactment. TCs using peer-to-peer rehearsals increased in their use of Uptake-Literal moves at a higher rate when in the classroom setting compared to TCs using VRS. That is, when facilitating number talks with elementary students, TCs who rehearsed in the peer-to-peer settings increased in their use of moves that positioned students as passive participants more than did the TCs who rehearsed in virtual simulations. TCs who rehearsed with peers perhaps received more unprompted responses from their peers and, therefore, when working with elementary aged students increased their use of Uptake-Literal moves as a way to elicit information in which they felt comfortable.
The differential increase in the frequency of Repeatmoves between contextd might also be connected to the shift from peers to children. As TCs entered into upper elementary classrooms, they may have repeated students’ short, literal responses as a way to acknowledge and process contributions. On the other hand, TCs who engaged in the VRS practiced eliciting thinking from student-avatars with real time coaching, and therefore, perhaps became more comfortable with the level of responses that approximated upper elementary students. The shift to an elementary classroom context was not as stark, and therefore, TCs who practiced in VRS did not revert to more literal type questioning or repeating.
For TCs who rehearsed with VRS, the increase in Uptake, Pushback, and Connection moves coupled with a difference in Uptake-Literalmoves depicted discussions where students had more opportunities to explain and connect their thinking in open-ended ways. A qualitative examination of the transcripts will help determine patterns with these moves to better understand the opportunities for students and changes in TCs’ practice.
Conclusion
In summary, this study provides empirical evidence in support of the assertion that VRS can support elicitation skill development as effectively as can more traditional peer-to-peer rehearsal contexts and can also enhance TCs facilitation of mathematical discussions in authentic elementary classrooms settings. Results from the statistical analyses show that TCs in both settings changed similarly across time except for their use of Uptake Literal and Repeatmoves.
The similarity in changes with all other moves between groups provide evidence that virtual simulations have the potential to provide comparable contexts for rehearsals. That is, the changes in the development of certain eliciting skills are similar across both groups regardless of virtual or peer-to-peer rehearsal. Therefore, development is not being thwarted by one instructional context. Previous research has documented positive engagement of TCs and in-service teachers with virtual simulations (e.g., Kaufman & Ireland, 2016; Straub, Dieker, Hughes et al., 2014), and these similarities further support VRS as a viable context.
This comparative look at virtual simulations is novel in that past research has not compared rehearsals with preservice teachers in different contexts. At the same time, the specific difference between the Uptake-Literal and Repeat moves between groups prompts further examination of the contexts and patterns in discussion to better understand what influenced differential change.
This study focused on one part of a larger project (Project INTERSECT) that creates science, technology, engineering and mathematics (STEM) VRS scenarios to expand practice-based teaching education (Grossman et. al, 2009) and attend to the specific needs of mathematics and science teacher development. The next steps within this work are to examine key patterns within the teacher moves used in both contexts (peer-to-peer and VRS) and qualitatively analyze the prompts and questioning used within each. This research will reveal detailed examples to better understand the differential use of Uptake-Literalmoves and further delineate similarities in other moves to better understand the affordance and limitation of each context. Furthermore, the coaching interactions within each context will be analyzed to shed light on differences and similarities that may be present within the contexts.
Last, work will continue to provide other teacher education programs with research-based scenarios that promote authentic contexts for TCs to rehearse high-leverage practices specific to STEM education. In conclusion, this work strives to provide teacher education programs with insight and resources to utilize VRS to promote development of eliciting skills that will promote student discussion and learning in elementary classrooms.
Note
This material is based upon work supported by the National Science Foundation under Grant No. 1725707. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
References
Anderson, L. W., Krathwohl, D. R., Airasian, P. W., Cruikshank, K. A., Mayer, R. E., Pintrich, P. R., Raths, J., & Wittrock, M.C. (2001). A taxonomy for learning, teaching, and assessing: A revision of Bloom’s Taxonomy of Educational Objectives (Complete edition). Longman.
Anthony, G., Hunter, J., & Hunter, R. (2015). Prospective teachers’ development of adaptive expertise. Teaching and Teacher Education, 49, 108-117 doi:10.1016/j.tate.2015.03010
Averill, R., Drake, M., Anderson, D., & Anthony, G. (2016). The use of questions within in-the-moment coaching in initial mathematics teacher education: enhancing participation, reflection, and co-construction in rehearsals of practice. Asia-Pacific Journal of Teacher Education, 44(5), 486-503.
Ayres, K. (2008). Video supports for teaching students with developmental disabilities and autism: Twenty-five years of research and development. Journal of Special Education Technology, 23(3), 1-8.
Ball, D., & Forzani, F. M. (2009). The work of teaching and the challenge for teacher education. Journal of Teacher Education, 60(5), 497-511.
Ball, D., Sleep, L., Boerst, T., & Hyman, B. (2009). Combining the development of practice and the practice of development in teacher education. Elementary School Journal, 109(5), 458-474.
Bartell, T., Wager, A., Edwards, A., Battey, D., Foote, M., & Spencer, J. (2017). Toward a framework for research linking equitable teaching with the standards for mathematical practice. Journal for Research in Mathematics Education, 48(1), 7-21.
Bell, N. D. (2007). Microteaching: What is it that is going on here? Linguistics and Education, 18(1), 24-40.
Bernard, H. R. (2011). Research methods in anthropology: Qualitative and quantitative approaches. AltaMira Press.
Biber, D., Conrad, S., & Reppen, R. (1998). Corpus linguistics: Investigating language structure and use. Cambridge University Press.
Boggs, J. G., Mickel, A. E., & Holtom, B. C. (2007). Experiential learning through interactive drama: An alternative to student role plays. Journal of Management of Education, 31(6), 832-858. doi: 10.1177/1052569062944952.
Bousfield, T., Dieker, L., Hughes, C., & Hynes, M. (2016). Proceedings of National TLE TeachLivETM Conference. Orlando, FL.
Boyatzis, R. E. (1998). Transforming qualitative information: Thematic analysis and code development. Sage Publications.
Bradley, E. G., & Kendall, B. (2014). A review of computer simulations in teacher education. Journal of Educational Technology Systems, 43(1), 3-12. doi:10.2190/ET.43.1.b
Carpenter, T. P., Franke, M. L., Johnson, N.C., Turrou, A. C., & Wager, A. A. (2016). Young children’s mathematics: Cognitively guided instruction in early childhood education. Portsmouth, NH: Heinemann.
Cazden, C. B., & Beck, S. W. (2003). Classroom discourse. In A. C. Graesser, M. A. Gernsbacher, & S. R. Goldman (Eds.), Handbook of discourse processes (pp. 165–197). Lawrence Erlbaum Associates Publishers.
Chapin, S. H., O’Connor, C., & Anderson, N. C. (2009). Classroom discussions: Using math talk to help students learn, grades K-6 (2nd ed.). Math Solutions Publications.
Clift, R. T., & Brady, P. (2005). Research on methods courses and field experiences. In M. Cochran-Smith & K. Zeichner (Eds.), Studying teacher education: The report of the AERA panel on research and teacher education (pp. 309-324). Lawrence Erlbaum.
Cobb, P., & Jackson, K. (2011). Towards an empirically grounded theory of action for improving the quality of mathematics teaching at scale. Mathematics Teacher Education and Development, 13(1), 6-33.
Cochran-Smith, M. (1991). Learning to teach against the grain. Harvard Educational Review, 61(3), 279-311.
Cochran-Smith, M., & Lytle, S. L. (2001). Beyond certainty: Taking an inquiry stance on practice. In A. Lieberman & L. Miller (Eds.), Teachers caught in the action: Professional development that matters (pp. 45-58). Teachers College Press.
Correnti, R., Stein, M. K., Smith, M. S., Scherrer, J., McKeown, M., Greeno, J., & Ashley, K. (2015). Improving teaching at scale: Design for the scientific measurement and learning of discourse practice. In L.B. Resnick, C. Asterhan, & S. Clarke (Eds.), Socializing intelligence through academic talk and dialogue. (pp. 315-332). American Educational Research Association. http://dx.doi.org/10.3102/978-0-935302-43-1_25
Darling-Hammond, L. (2006). Constructing 21st-century teacher education. Journal of Teacher Education, 57(3), 300-314.
Darling-Hammond, L. (2012). Powerful teacher education: Lessons from exemplary programs. John Wiley & Sons.
Dawson, M. R., & Lignugaris/Kraft, B. (2017). Meaningful practice: Generalizing foundation teaching skills from TLE TeachLivE™ to the classroom. Teacher Education and Special Education, 40(1), 26-50. doi:10.1177/0888406416664184
DeCuir-Gunby, J. T., Marshall, P. L., & McCulloch, A. W. (2011). Qualitative research, technology, and global change. In N. K. Denzin & M. D. Giardina (Eds.), Qualitative inquiry and global crises (pp. 79-96). Left Coast Press.
Dieker, L. A., Hughes, C. E., Hynes, M. C., & Straub, C. (2017). Using simulated virtual environments to improve teacher performance. School-University Partnerships, 10(3), 62-81.
Dieker, L., Hynes, M., Hughes, C., & Smith, E. (2008). Implications of mixed reality and simulation technologies on special education and teacher preparation. Focus on Exceptional Children, 40(6), 1-21.
Dieker, L. A., Rodriquez, J. A., Lignugaris/Kraft, B., Hynes, M. C., & Hughes, C. E. (2014). The potential of simulated environments in teacher education: Current and future possibilities. Teacher Education and Special Education, 37(1), 21-33.
Dieker, L. A., Straub, C. L., Hughes, C. E., Hynes, M. C., & Hardin, S. (2014). Learning from virtual students. Educational Leadership, 71(8), 54-58.
Ghousseini, H., & Herbst, P. (2016). Pedagogies of practice and opportunities to learn about classroom mathematics discussions. Journal of Mathematics Teacher Education, 19(1), 79-103.
Girod, M. & Girod, G.R. (2008). Simulation and the need for practice in teacher preparation. Journal of Technology and Teacher Education, 16(3), 307-337.
Goldhaber, D., Krieg, J. M., & Theobald, R. (2017). Does the match matter? Exploring whether student teaching experiences affect teacher effectiveness. American Educational Research Journal, 54(2), 325-359.
Gotwals, A., & Birmingham, D. (2016). Eliciting, identifying, interpreting, and responding to students’ ideas: Teacher candidates’ growth in formative assessment practices. Research in Science Education, 46(3), 365-388. http://dx.doi.org/10.1007/s11165-015-9461-2
Grossman, P., Compton, C., Igra, D., Ronfeldt, M., Shahan, E., & Williamson, P. (2009). Teaching practice: A cross-professional perspective. Teachers College Record, 111(9), 2055-2100.
Hixon, E., & So, H. J. (2009). Technology’s role in field experiences for preservice teacher training. Educational Technology & Society, 12, 294-304.
Hruschka, D. J., Schwartz, D., St. John, D. C., Picone-Decaro, E., Jenkins, R. A., & Carey, J. W. (2004). Reliability in coding open-ended data: Lessons learned from HIV behavioral research. Field Methods, 16(3), 307-331.
Kaufman, D., & Ireland, A. (2016). Enhancing teacher education with simulations. TechTrends. 60, 260-267. doi: 10.1007/s11528-016-0049-0
Kazemi, E., Franke, M., & Lampert, M. (2009). Developing pedagogies in teacher education to support novice teachers’ ability to enact ambitious instruction. In R. Hunter, B. Bicknell, & T. Burgess (Eds.), Crossing divides: Proceedings of the 32nd annual conference of the Mathematics Education Research Group of Australasia (Vol. 1; pp. 11-30). MERGA.
Kazemi, E., Ghousseini, H., Cunard, A., & Turrou, A. C. (2016). Getting inside rehearsals: Insights from teacher educators to support work on complex practice. Journal of Teacher Education, 67(1), 18-31.
Kazemi, E., & Wæge, K. (2015). Learning to teach within practice-based methods courses. Mathematics Teacher Education and Development, 17(2), 125-145.
Krippendorff, K. (2009). Testing the reliability of content analysis data: What is involved and why. In K. Krippendorff & M.A. Bock (Eds.), The content analysis reader (pp. 350-357). Sage.
Kovalainen, M., & Kumpulainen, K. (2005). The discursive practice of participation in an elementary classroom community. Instructional Science, 33(3), 213-250.
Lampert, M., Beasley, H., Ghousseini, H., Kazemi, E., & Franke, M. (2010). Using designed instructional activities to enable novices to manage ambitious mathematics teaching. In M. K. Stein & L. Kucan (Eds.), Instructional explanations in the disciplines (pp. 129-141). Springer.
Lampert, M., Franke, M. L., Kazemi, E., Ghousseini, H., Turrou, A. C., Beasley, H., & Crowe, K. (2013). Keeping it complex: Using rehearsals to support novice teacher learning of ambitious teaching. Journal of Teacher Education, 64(3), 226-243.
Lampert, M., & Graziani, F. (2009). Instructional activities as a tool for teachers’ and teacher Educators’ learning. The Elementary School Journal, 109(5), 491-509.
Lee, C., Lee, T., Castle, R., Dickerson, D., Fales, H., & Wilson, C. (2018). Implementation of immersive classroom simulation activities in a mathematics methods course and a life and environmental science course. Journal of Interdisciplinary Teacher Leadership, 2(1), 3-17.
Levin, D. M., Hammer, D., & Coffey, J. E. (2009). Novice teachers’ attention to student thinking. Journal of Teacher Education, 60(2), 142-154.
Mehan, H. (1979). ‘What time is it, Denise?”: Asking known information questions in classroom discourse. Theory into Practice, 18(4), 285-294.
Michaels, S., & O’Connor, C. (2015). Conceptualizing talk moves as tools: Professional development approaches for academically productive discussion. In S. Michaels & C. O’Connor (Eds.), Socializing intelligence through talk and dialogue (pp. 347-362). American Educational Research Association. http://dx.doi.org/10.3102/978-0-935302-43-1_27
O’Callaghan, C., & Piro, J. (2016). Virtual simulations in a practice-based teacher education. The Field Experience Journal, 17(1), 94-118
Parrish, S. (2010). Number talks: Helping children build mental math and computation strategies, grades K-5. Math Solutions.
Parrish, S. D. (2011). Number talks build numerical reasoning. Teaching Children’s Mathematics, 18(3), 198-206.
Peterson-Ahmad, M., Pemberton, J., & Hovey, K. (2018). Virtual learning environments for teacher preparation, Kappa Delta Pi Record, 54(4), 165-169. doi: 10.1080/00228958.2018.1515544
Pretti-Frontczak, K., Brown, T., Senderak, A., & Walsh, J. (2005). A preliminary investigation of the effectiveness of CaseQuests in preparing family-guided and technologically-competent early childhood interventionists. Journal of Computing in Teacher Education, 21(3), 87-93.
Rieg, S.A., & Wilson, B. (2009). An investigation of the instructional pedagogy and assessment strategies used by teacher educators in two universities within a state system of higher education. Education 130(2), 277-294.
Saldana, J. (2016). The coding manual for qualitative researchers. Sage.
Scherrer, J., & Stein, M. K. (2013). Effects of a coding intervention on what teachers learn to notice during whole-group discussion. Journal of Mathematics Teacher Education, 16(2), 105-124.
Shaughnessy, M., & Boerst, T. A. (2017). Uncovering the skills that preservice teachers bring to teacher education: The practice of eliciting a student’s thinking. Journal of Teacher Education, 69(1), 40-55. https://doi.org/10.1177%2F0022487117702574
Shaughnessy, M., Boerst, T. A., & Farmer, S. O. (2018). Complementary assessments of prospective teachers’ skill with eliciting student thinking. Journal of Mathematics Teacher Education, 22, 1-32.
Smith, M. S., & Stein, M. K. (1998). Selecting and creating mathematical tasks: From research to practice. Mathematics Teaching in the Middle School, 3(5), 344-50.
Stein, M. K., Ashley, K., Correnti, R., McKeown, M., Smith, P., Chisholm, & Scherrer, J. (2013). Analyzing teacher moves framework. Unpublished Measure. University of Pittsburgh.
Straub, C., Dieker, L., Hynes, M., & Hughes, C. (2014). Using virtual rehearsal in TLE TeachLivE mixed reality classroom simulator of mathematics teachers (2014 TeachLivE National Research Project: Year 1 Findings). University of Central Florida.
Straub, C., Dieker, L., Hughes, C., & Hynes, M. (2014, February 6). Mixed-reality computer simulation: A new paradigm for higher education. Presentation delivered at the 6th Annual Conference on Higher Education Pedagogy, Blacksburg VA.
Straub, C., Dieker, L., Hynes, M., & Hughes, C. (2016). TeachLivE Year 3 Research Report. http://teachlive.org/wp-content/uploads/2016/09/2016-TeachLivE-Year-3-Technical-Report.pdf
Sweeney, J., Milewski, A., & Amidon, J. (2018). On-ramps to professional practice: Selecting and implementing digital technologies for virtual field experiences. Contemporary Issues in Technology and Teacher Education, 18(4), 670-691. https://citejournal.org/volume-18/issue-4-18/general/on-ramps-to-professional-practice-selecting-and-implementing-digital-technologies-for-virtual-field-experiences
Syed, M., & Nelson, S. C. (2015). Guidelines for establishing reliability when coding narrative data. Emerging Adulthood, 3(6), 375-387.
Teaching Works. (2011). High leverage teaching practices. http://www.teachingworks.org/work-of-teaching/high-leverage-practices
Thompson, J., Windschitl, M., & Braaten, M. (2013). Developing a theory of ambitious early-career teacher practice. American Educational Research Journal, 50(3), 574-615.
Tyminski, A. M., Zambak, V. S., Drake, C., & Land, T. J. (2014). Using representations, decomposition, and approximations of practices to support prospective elementary mathematics teachers’ practice of organizing discussions. Journal of Mathematics Teacher Education, 17(5), 463-487.
Wæge, K., & Fauskanger, J. (2020). Teacher time outs in rehearsals: in-service teachers learning ambitious mathematics teaching practices. Journal of Mathematics Teacher Education. https://doi.org/10.1007/s10857-020-09474-0
![]()