The use of video as a tool for teacher learning has a long history (Brophy, 2003; Gaudin & Chaliès, 2015; Sherin, 2004). Ways video has been utilized at different historical times reflect values and objectives related to teacher preparation and professional development of particular eras (Santagata, Gallimore, & Stigler, 2005). Currently, various countries around the world explicitly promote an approach to instruction that is supported by constructivist theories of learning (Greeno, Collins, & Resnick, 1996; Piaget, 1952). This approach, often referred to as student-centered instruction, places a focus on teaching practices that build on and are responsive to learners’ understandings. In the U.S., this view of teaching has been prominent in scholarly communities for quite some time (e.g., Carpenter et al., 1997; Schoenfeld, 1992) and has received new attention with the recent introduction of new curriculum standards (Common Core State Standards Initiative, 2010).
Video has been shown to be a particularly promising tool for shifting views of teaching from an activity highly directed by teachers to an activity in which student thinking is at the center of the teaching-learning process. Video can be paused and reviewed multiple times, allowing teachers to slow down the work of teaching and to examine teaching and learning interactions as they occur during classroom lessons (Brophy, 2003). Lesson episodes can be singled out and studied carefully to attend to student subject matter thinking and their reactions to particular teaching decisions (Hatch & Grossman, 2009; Lampert & Ball, 1998; Schoenfeld, 2017).
Analyses of classroom videos guided by structured protocols can support teachers not only to develop student-centered views of teaching, but also practices that are responsive to student thinking (Sherin & van Es, 2009). In mathematics education research, video has been found to facilitate teacher analysis of student mathematical thinking and learning in the midst of instruction (Stockero, 2008; van Es & Sherin, 2002) and to promote deep reflection about student learning and next steps after instruction (Jacobs, Lamb, & Philipp, 2010; Jacobs, Lamb, Philipp, & Schappelle, 2011; Santagata & Guarino, 2011).
Attention to student thinking and learning through video analysis has also prompted the design of video-enhanced teacher professional development programs that have incorporated close analyses of student learning into broader goals, such as structured analysis of teaching effectiveness and development of teacher professional vision and judgment (Blomberg, Renkl, Sherin, Borko, & Seidel, 2013; Borko, Jacobs, Eiteljorg, & Pittman, 2008; Santagata, 2009; Seago, 2004; Stürmer, Seidel, & Schäfer, 2013). Finally, studies focused on the development of measures of teacher competence have documented that teachers’ ability to analyze student thinking as portrayed in brief video clips of classroom lessons is predictive of their teaching effectiveness (Kersting, Givvin, Thompson, Santagata, & Stigler, 2012).
Authors engaged in this work have highlighted various features of attention to student thinking that reflect important aspects of teacher competence. For example, research on teacher participation in video clubs and its effects on teaching practices has reported teachers’ increased attention to details of student mathematics thinking, as well as various strategies teachers adopted to make space for student thinking in their instruction. These strategies include probing students to elaborate on their thinking, publicly recognizing student ideas, providing time during lessons for students to think extensively about problem solutions, being open to a variety of ways of thinking about mathematical ideas, and positioning oneself as a learner by listening carefully and building on student ideas during teaching (van Es & Sherin, 2010).
Similarly, in the context of teacher preparation, research finds that preservice teachers who engage in systematic analyses of student thinking in their coursework are able to create opportunities in their classroom lessons to see student thinking through questioning and tasks that make student thinking visible. In addition, they attend to student thinking and they pursue student ideas to learn more about their thinking during instruction (Santagata & Yeh, 2014; van Es & Sun, 2015).
An area that needs further research focuses on examining ways student-centered analyses of video impact teachers’ practices beyond classroom teaching. The work of teaching includes two additional components that are fundamental to teaching effectiveness: planning and reflection. In the present study, we focused on teacher reflective practices and, more specifically, on reflection about teaching effectiveness.
Little is known about ways teachers use evidence of student thinking to reflect on the effectiveness of teaching and the impact of video analyses on this process. The existing research in this area highlights three important aspects. First of all, for reflection on the effectiveness of teaching to be productive, teachers need to focus on specific details of student thinking about the content. In addition, they need to consider evidence of student thinking and learning that is relevant to the particular teaching episode under examination. In other words, they need to select evidence that is directly relevant to the learning objectives of the teaching episode. If they want to make claims about what worked and what did not in a lesson, claims need to be substantiated in terms of student progress toward the lesson learning goals.
Finally, teachers need to select evidence that reveals student subject-matter thinking. If a lesson’s objective is to develop student understanding of addition of fractions, evidence of students’ effective use of an algorithm for adding fractions is revealing of student procedural fluency, but not revealing of student understanding of fraction addition (Bartell, Webel, Bowen, & Dyson, 2013; Jansen & Spitzer, 2009). Prior work the first author has conducted found that preservice teachers who participated in a video-enhanced course were better able than a control group to identify evidence of student learning that was both relevant and revealing when assessing the effectiveness of teaching episodes portrayed in brief video clips (Yeh & Santagata, 2015).
The study summarized here built on this work but also extended it in two ways. First, it examined whether preservice teachers’ experiences with video analyses during teacher preparation had long-lasting effects on their reflective practices once they entered the profession. In their review of research on video and teacher learning, Gaudin and Chaliès (2015) highlighted the need for research to attend to the impact that video analyses have not only in the short term, but throughout teachers’ professional careers. Specifically, we examined whether teachers who had opportunities to analyze student thinking and learning during teacher preparation, continued to do so when they reflected on their teaching effectiveness as full-time teachers. In addition, we explored a novel measure to document ways teachers engage in reasoning about the effectiveness of their teaching.
The study addressed the following questions:
- Do teachers who experienced a video-enhanced teacher preparation course focused on student-centered analyses of lesson effectiveness incorporate such analyses in their reflections about their teaching effectiveness at the end of their first year of full-time teaching?
- Do their reflections about their teaching effectiveness differ compared to reflections of teachers who did not experience such a course?
Study Methods and Methods Course Curricula
Participants and Study Design
Twenty-four elementary-school teachers participated in the study. All teachers attended the same teacher preparation program at a public university in the United States. The program consisted of 1-year of postbachelor’s degree coursework and parallel field-based experiences in local schools.
In order to graduate and receive their teaching credential, teachers had to pass their coursework with at least a B letter grade (where A is the highest grade) and pass a performance assessment (i.e., the Performance Assessment for California Teachers). Teachers were 21 female and 3 male. Study participants are a subsample of a larger group of 112 preservice teachers who participated in a larger project. The 24 participants were chosen found a full-time teaching job right after graduation. Eleven attended a video-enhanced methods course, and 13 were in the control group.
Participants were randomly assigned prior to the beginning of the program to attend two different versions of a mathematics methods course, while all other coursework was the same. The Learning to Learn from Mathematics Teaching (LLMT) course engaged teachers in systematic analyses of videos of teaching episodes while developing teaching practices aligned with the new Common Core curriculum standards. The Mathematics Methods Course (MMC) shared the same objectives of preparing teachers to implement practices aligned with the new standards and, thus, focused on student mathematical thinking but did not engage them in video analyses.
Because we wanted to maintain the hours of coursework equal between groups, MMC participants discussed more mathematics topics in depth, while LLMT participants focused only on the main topics of the elementary-school mathematics curriculum. Both courses lasted 20 weeks (i.e., two quarters) and met for approximately 3 hours a week, for a total of 60 hours of instruction. While attending the course, participants were also randomly assigned to fieldwork experiences and spent 1 day per week in an elementary-school classroom during the first 10 weeks and 3 days per week during the second 10 weeks, gradually assuming more teaching responsibilities.
Video-Enhanced Curriculum
The LLMT mathematics methods course (the experimental condition) was structured around two mathematics domains: whole numbers and rational numbers. During the first quarter of the course, the preservice teachers learned about student mathematics thinking and its development. They also learned to attend to the details of student thinking and to infer student understanding through guided analyses of video clips of children solving mathematics problems and of video of classroom lessons taught by experienced teachers. These activities built on extensive research in this area and on two projects in particular: Cognitively Guided Instruction (Carpenter, Fennema, Franke, Levi, & Empson, 1999; Empson & Levi, 2011) and the New Zealand Numeracy Project (http://nzmaths.co.nz/numeracy-projects).
Preservice teachers then practiced to elicit student thinking in their own teaching by conducting a videotaped interview with a student who was asked to solve a series of mathematics problems. Subsequently, they refined their questioning and analysis skills by working in triads and taking turns at leading the planning, teaching, and critical analysis of their videotaped minilesson with a small group of students.
During the second academic quarter, this work was extended to the domain of rational numbers. This quarter also included participation in the collaborative design of a week-long unit on fractions. Through the use of digital video, copies of student work, and a blog, preservice teachers followed the course instructor into a fourth-grade classroom to observe instruction and analyze the nature of children’s understanding represented in their oral and written work. They built on these observations and analyses to provide suggestions on lesson plans, next steps, revisions, and solutions to problems of practice that arose. This experience culminated in a final in-person visit to the classroom during which they observed the last lesson in the sequence and debriefed with the instructor. Concurrently, preservice teachers began to plan lesson units and take a more active role in the mathematics classroom at the school in which they were placed for student teaching.
Analyses of teaching were guided by the Lesson Analysis Framework. This framework provides a structure for analyzing the process of teaching and learning in a lesson or shorter instructional episode and focuses on four fundamental steps: (a) specification of learning goals; (b) analysis of evidence of student progress and/or difficulties; (c) reasoning about impact of teaching decisions on student thinking and learning; and (d) suggestions for next steps and instructional improvement (Hiebert, Morris, Berk, & Jansen, 2007; Santagata, Zannoni, & Stigler, 2007).
The visual (Figure 1) illustrates the analysis components as well as the competencies that we conjectured teachers develop through their engagement in this process.
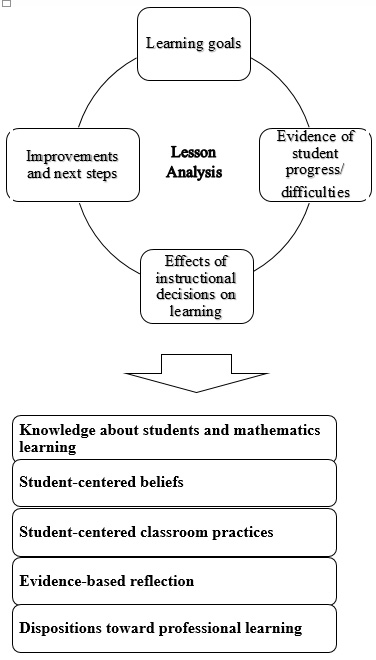
Several studies have examined the use of this framework with both preservice and in-service teachers and have reported overall positive impact on teachers’ abilities to attend to student thinking and use evidence of student thinking and learning to reason about the teaching-learning process (Krammer, Hugener, Frommelt, der Maur, & Biaggi, 2015; Santagata, 2010; Santagata & Angelici, 2010; Santagata & Guarino, 2011; Santagata et al., 2007). Specifically, a study that focused on the LLMT course described above and involving a larger sample of preservice teachers than the current study found significant group differences on several measures. Preservice teachers attending the LLMT course improved in their ability to analyze student thinking to a greater degree than the control group. These teachers were also observed to build on student thinking more during instruction and to attend to student thinking when asked to reflect on their students’ progress towards the lesson learning goal. Finally, a significant difference was also found with respect to the LLMT group of preservice teachers’ alignment with the belief that lessons should be centered on student thinking (Santagata, Yeh, & Mercado, in press).
The Mathematics Methods Course
The MMC course (the control condition) was structured around the most adopted mathematics education textbook in the United States, Elementary and Middle School Mathematics: Teaching Developmentally, by Van de Walle, Karp and Bay-Williams (2013). Preservice teachers were given opportunities to learn about children’s development of mathematical understandings and student-centered teaching practices, such as questioning, classroom discussions, and use of mathematical representations and manipulatives to foster children’s conceptual understanding.
The course differed from the LLMT course in that it did not include opportunities to conduct video-enhanced, detailed analyses of student thinking and learning nor structured reflections on teaching and learning. The time preservice teachers in the LLMT group spent on these activities was spent by the control group learning to teach mathematics topics of the K-6 curriculum other than whole numbers and operations and rational numbers. MMC participants focused mostly on enactment of student-centered practices, while LLMT participants enacted and reflected on practices through the aid of video.
Measures
Participants were administered a survey at the end of their first year of teaching through an online survey provider. For the purposes of this study, we limited analyses to questions that focused on teachers’ reflections on two lessons they had just taught. We asked teachers to think about the last math lesson they taught (and call it Lesson 2) and the lesson prior to that (and call it Lesson 1) and answer a few questions.
For each lesson, questions elicited description of lesson learning goals as well as a rating of lesson effectiveness and a rationale for their evaluation. The final questions elicited a comparison of effectiveness between the two lessons, along with their rationale in order to provide further specific evidence of effectiveness. Thus, the questions for each of the two lessons followed this sequence:
- What was the learning goal of Lesson 1?
- Please rate the effectiveness of Lesson 1 using the 5-point rating scale (i.e., ranging from 1, not at all effective, to 5, very effective)
- Please explain your rating for Lesson 1.
The same questions followed for Lesson 2 (i.e., questions 4, 5, and 6). The final questions eliciting a comparison of effectiveness between the two lessons were as follows:
- Which lesson was more effective? How do you know?
- Describe in detail what evidence you would share to demonstrate that the lesson you chose was the most effective.
Participants’ responses were scored according to two separate 3-point rubrics. The first rubric (see Table 1) captures the focus and quality of evidence teachers provided to justify the rating of their lessons and the comparison between the effectiveness of the two lessons. This rubric was applied to all open-response questions.
Table 1
Focus and Quality of Evidence Rubric
| Question: To what extent does the teacher’s evidence of lesson effectiveness focus on student thinking and learning and with what level of specificity does the teacher discuss such evidence? | |
| Score | Sample Response |
| 3 High/Exemplary. A score of “3” is assigned when the evidence of effectiveness is directly linked to the lesson learning goal(s) and to (a) student specific mathematical content understandings and/or difficulties (e.g., misconceptions) or (b) student engagement in math practices (i.e., CCSS math practices) and/or (c) use of specific mathematics academic language. | I believe my lesson was effective because of student work and data from their formative and summative assessments. In student work, students were able to describe academic language and key vocabulary, such as, “identify,” “patterns,” and “equations.” Students used prior knowledge to talk about identify as a means to look for or know for certain, patterns as a means of something that is repeated or happening the same way each time, and equations as a means of number sentences using variables. During student talk and partnerships, students were able to explain their thinking when tackling a problem, talking in complete sentences of what they noticed or what is happening to the numbers each time. They also talked about how x and y are variables and that they can represent different values at different times. Some students also used the word “relationship” between x and y when talking about the pattern. They used my sentence frame of, “when x is… y is…” and talked about the relationship that was happening each time, such as adding or subtracting a value. When talking about equations, students were able to say that the rule or pattern each time will fit the equation y = x +/- a value. The pattern is what you add or subtract each time. The data from the summative assessments show me that students reached the goal. |
| 2 Mid-range/Developing. A score of “2” is assigned when the evidence of effectiveness is generally linked to lesson learning goal(s) and to (a) student mathematical content understandings and/or difficulties (e.g., misconceptions) and/or (b) student engagement in math practices (i.e., CCSS math practices), and/or (c) use of mathematics academic language. The teacher mentions strategies s/he used to collect evidence of student mathematics learning during the lesson. The evidence is described in more general terms than in responses that receive a score of 3. | I would provide the students with a question orally and give them time to think about their answer. When about 10-15 seconds had passed, I asked a volunteer to come up to the board, color in the correct answer(s) on the hundred chart, and explain his/her reasoning. Some of the students had difficulty with the oral questions, but understood the problem once it was shown up on the board. |
| 1 Low/Weak/Not present. A score of “1” is assigned when the response focuses on instructional strategies the teacher used and/or when evidence of student progress toward the lesson learning goal or of difficulties is vague or very general. | While walking around and working with students I had fewer students frustrated and helpless the second day. More could work independently after help. |
We were interested in examining whether the evidence teachers focused on was linked to the lesson learning goal(s) as well as in the level of specificity of the evidence in relation to (a) mathematic content understandings and/or difficulties, (b) engagement in math practices included in the curriculum standards, and (c) use of mathematics academic language. The two sets of questions describing lesson learning goals and evaluating effectiveness were both assigned a score of 1, 2, or 3 (i.e., questions 1-3 and 4-6). In addition, the questions comparing the effectiveness of the two lessons (i.e., questions 7 and 8) were also assigned a score of 1, 2, or 3. A composite score was then created for this dimension of focus and quality of evidence; thus, scores ranged from 3 to 9.
The second rubric (see Table 2) captures teachers’ attention to individual or subgroups of learners. That is, the degree to which the teachers attend to understandings or performance of the lesson learning goal beyond the level of the whole class. The two sets of questions focusing on the assessment of each lesson were both scored (i.e., questions 1-3 and 4-6). A composite score was then created for this dimension of attention to individual learners; thus, the scores ranged from 2 to 6.
Table 2
Attending to Individual or Subgroups of Learners Rubric
| Question: To what extent does the teacher’s evidence of lesson effectiveness identify individuals’ or subgroups’ progress towards the learning goal(s) and/or learning needs? | |
| Score | Sample Response |
| 3 High/Exemplary. Description of students’ understanding or performance and subsequent learning needs specifically (and in detail) identifies differences/patterns in individuals’ or subgroups’ understanding or performance (beyond whole class) as evidence for effectiveness. | Many students used place value strategies to solve the problem, and no one really compensated and turned 39 into 40 and 42 into 41. I was anticipating some of the higher students would use that strategy so that I could highlight that during the share out. Instead, we had our share out and at the end I prompted students to see if there was any way that we could change the numbers to make them easier to add together, and many students were quick to realize that you could compensate and then said that 4+4 was like 40+40 and then you just add one more. I rated the lesson a 3 because students didn’t start out using a compensating strategy, but were able to do it after some discussion. |
| 2 Mid-range/Developing. Description of students’ understanding or performance and subsequent learning needs identifies some differences/patterns in student performance as evidence for effectiveness. Some differences in levels of understanding are described, but the description is mainly a whole class analysis and the evidence focuses on what the students did right or wrong. | Students were all able to correctly complete the activity (which was a paper-and-pencil worksheet) and then participate in a game that required the completing of math facts on a SMART Board quickly and accurately. Nearly every student was able to show fluency, and those who were not fluent could at least complete the activity using manipulatives, drawing pictures or using fingers. |
| 1 Low/Weak/Not present. Description of differences/patterns of individuals’ or subgroups’ understanding or performance (beyond whole class) and subsequent learning needs is not present as evidence for effectiveness. | This was simply practicing a skill/concept. I have already taught this concept extensively using hands on materials, acting out subtraction stories with students, playing games etc. I wanted students to be able to complete the problems with pencil and paper in the traditional way as well, and when I checked my students’ work and asked them about the problems they were working I saw that nearly all my students were able to complete the problems with few issues. |
The survey questions differed in their phrasing from the questions LLMT participants were exposed to during teacher preparation through the Lesson Analysis Framework. Nonetheless, there were clear parallelisms between the two sets of questions, as they both asked to reason about the effectiveness of teaching. We were interested in examining whether systematic learning opportunities are necessary for teachers to learn to conduct evidence-based reflections on the effectiveness of their practices or whether teachers develop this reflective habits informally and simply through teaching experience.
The comparison between LLMT and MMC participants allowed us to single out specifically the impact of video-based reflections during teacher preparation on teachers’ reflective practices. Since working on these practices during teacher preparation requires course instructors to make important decisions about prioritizing certain learning activities versus others in the methods courses, it is important to make sure that video-based and reflection-focused activities afford learning of practices that most teachers would not otherwise develop.
In addition, despite the similarities in the approach to reflection promoted in the LLMT course and the study’s survey questions, over 1 year passed between reflection activities teachers experienced during teacher preparation (which occurred during the months of September through March) and the time teachers completed the study measure (May of the following year). This allowed us to examine whether LLMT participants seemed to internalize the reflection practices to which they were exposed during teacher preparation and continued to engage in them once they entered the profession. In addition, the study survey questions required transfer of those practices to a task neither LLMT or MMC teachers had engaged in before; that is, the comparison between the effectiveness of two lessons they had taught.
Teachers’ survey responses were blinded for group membership and scored by two independent raters. Interrater reliability was calculated as percent agreement and reached .80. Cases of disagreement were reviewed and discussed until agreement was reached. Because of the small sample size, groups were compared using descriptive statistics complemented by the close analysis of two cases.
Results
This study examined the long-term results of a teacher preparation course that utilized video of instructional episodes to develop teachers’ appreciation of student mathematical thinking and abilities to attend to the details of such thinking. The course also exposed teachers to opportunities to reflect systematically on teaching and to use evidence of student learning to assess the effectiveness of instructional decisions. Before quantitative findings are presented through comparisons of groups’ average scores, responses from two participants are described to illustrate how the survey questions functioned as a tool for capturing teachers’ evidence-based reasoning about teaching and how teachers’ responses varied in relation to the dimensions of interest (i.e., focus and quality of evidence and attention to individuals or subgroups of learners).
Two Contrasting Cases
Robert (all names are pseudonyms) was in the MMC group during teacher preparation and was a fifth-grade teacher at a public elementary school when he completed the survey at end of his first year of teaching. The lefthand column in Table 3 reports Robert’s responses to the survey questions.
Table 3
Group Participants’ Survey Responses
| Survey Question | MMC Response | LLMT Response |
| What was the learning goal of Lesson 1? | The learning goal of lesson 1 was for students to have an understanding of the base-ten system with the assistance of a place value chart. | Students will be able to subtract a small number from a larger number. |
| Please rate the effectiveness of Lesson 1. | 3 | 4 |
| Please explain your rating for Lesson 1. | This year, our school district has moved toward a more scripted math curriculum. While it has many strong components, there are also flaws. Initially, I attempted to stick with the script, following district protocol. However, observing student reactions, the script would not be suitable for my students. I then moved away from it and into small groups so students that had a strong grasp of the content could continue while I assisted those that struggled with it. | Students understood that they had to take away the small number from the larger number. They drew pictures to demonstrate the problem. For example, with the problem 5-1, most understood that they needed to start with the number 5, so they drew 5 circles. They also understood that the second number was the number they needed to take away, so after they drew the 5 circles they would cross out one circle, leaving four circles left. So their final answer would be 5 – 1 = 4. The pictures were something visual that was very helpful to my students, especially the ELLs. This also seemed to be easier than subtraction, as this was something that they could draw/demonstrate themselves without necessarily having to use cubes or other manipulatives. Some students were initially confused by the sign, and still thought that they were adding (“putting together”). I had to take a moment to demonstrate the difference between the addition sign and the subtraction sign, and review what addition meant (putting things together). |
| What was the learning goal of Lesson 2? | The goal of lesson two was for students to apply knowledge from the previous place value lesson and complete base-ten multiplication problems without a place value chart. | Students would solve a subtraction problem using their fingers rather than illustrating the problem. |
| Please rate the effectiveness of Lesson 2. | 4 | 3 |
| Please explain your rating for Lesson 2. | Students were able to make connections more efficiently with this lesson. They were able to clarify errors made in the previous lesson and continue through the lesson. | Some students would still initially add when they saw the subtraction problem. They would hold up fingers on both hands to demonstrate addition rather than subtraction. Once again, the difference between the addition and subtraction sign had to be addressed. Holding up fingers seemed to be more confusing than drawing out the problem. A large number of ELLs [English Language Learners] struggled with this. For example, if the problem was 5-1, they would know to start with 5 fingers. However, they quickly dropped the other fingers, holding up only 1 finger and claiming that to be the final answer. So they would say that 5-1=1. I had to explain several times that similar to when drawing out the circles, the first number is the number you start with and the second number is the amount you take away. So, if you start with 5 fingers, you only take away 1 finger because that’s what the problem says. Then you count how many fingers you have left to get your answer. |
| Which lesson was more effective? How do you know? | Lesson 2 Throughout lessons, I am constantly checking in with students so that I can assess their understanding and providing opportunities for them to share their self-assessments. | Lesson 1 Based on students’ independent practice and exit tickets, they showed more understanding after the first lesson. On the IP [independent practice] of the second lesson, some students resorted to drawing out the circles to solve their subtraction problems. |
| Describe in detail what evidence you would share to demonstrate that the lesson you chose was the most effective. | Throughout lessons, I am constantly checking in with students so that I can assess their understanding and providing opportunities for them to share their self-assessments. This can come through simple signals from the students, questions that they ask or I ask, and through the products that the students produce. | I would share students’ independent practice pages. In the first lesson, the subtraction problems were formatted horizontally so there was space for them to illustrate the problem. Most students got the problems correct, with the exception of a few miscountings (however the problems were still illustrated correctly, with the number of circles to start with and the number of circles that needed to be taken away). In the second lesson, the subtraction problems were formatted vertically so that there was no space for them to illustrate, urging them to use their fingers to solve the problem. There were many more errors from student work. |
| Note. Effectiveness ratings use a 5-point rating scale. 5 = high; 1 = low. | ||
Robert’s rationale for his Lesson 1 evaluation of a 3 (i.e., midway between not at all effective, 1, and very effective, 5) was vague along the Focus and Quality of Evidence dimension, in that it lacked a direct connection to his lesson learning goal of students coming to understand the base-ten system through the use of a place value chart. He discussed his instructional decisions as attempts to react to challenges he saw in his student learning, but he provided no details about difficulties students encountered in understanding the base-ten system that prompted him to deviate from the school district’s scripted math curriculum.
Similarly, in his rationale for his Lesson 2 evaluation of a 4 (i.e., almost at a 5, very effective), the response did not specify which “connections” students were able to make in relation to using prior place value knowledge to complete base-ten multiplication problems. Finally, Robert offered weak evidence for his final evaluation that Lesson 2 was more effective than Lesson 1. He claimed to “assess their understanding” but did not relate it to specific mathematical understandings from the lesson learning goal.
In the Attention to Individual or Subgroups of Learners dimension, Robert’s responses also tended to be vague. In his evidence of effectiveness for Lesson 1, he acknowledged some attention to individual learners in that he utilized “small groups so students that had a strong grasp of the content could continue while I assisted those that struggled with it.” This midrange level of evidence could have been bolstered with more specificity toward the nature of the “strong grasp,” as well as stating more exactly how he “assisted those that struggled with it.” His rationale for effectiveness for Lesson 2 contained no evidence of attention to individual learners.
Stephanie was in the LLMT group during teacher preparation and was a kindergarten teacher (i.e., first year of elementary school in the U.S.) when she completed the survey at the end of her first year of teaching. She provided consistently strong rationales for lesson effectiveness along both dimensions. In the Focus and Quality of Evidence dimension, for example, her evaluation of effectiveness for both lessons was squarely focused on students’ mathematical understanding. She described students’ specific understandings in relation to her lesson learning goal of subtracting a small number from a larger number.
The rationale for her evaluation that Lesson 1 was more effective than Lesson 2 stated, “They showed more understanding after the first lesson.” She then offered supporting details that further specified the students’ level of understanding and even explained the nature of how some students struggled with the learning goal.
In the Attention to Individual or Subgroup of Students dimension, Stephanie demonstrated a nuanced awareness of and attention to individual learners. Her rationales included descriptions of how the English learners in her class were specifically helped or hindered by certain visuals that she had incorporated into the learning goals.
While Stephanie did mention her own instructional strategies as a part of her evidence for lesson effectiveness, the function of these strategies served to support her claims that she was attending to the learning needs of this particular subgroup of students, the English learners in her class. Stephanie did not rely on her own instructional strategies as evidence but mentioned them as direct responses to students’ difficulties with the content. Thus, we attributed her with a strong awareness of differences in individuals’ or subgroups’ understanding beyond that of the whole class.
Group Differences
These two cases illustrated differences that were found in the two groups. In Table 4 is reported the groups’ average composite score for the Focus and Quality of Evidence scoring rubric and the average composite score for Attention to Individual and Subgroups of Learners rubric. In addition, it also reports the average rating of lesson effectiveness participants gave to the two lessons.
Table 4
Average Scores on Focus and Quality of Evidence and Attention to Individual and Subgroups of Learners Rubrics and Mean Lesson Rating per Group
| Dimension | LLMT Mean (SD) | MMC Mean (SD) |
| Focus and Quality of Evidence | 6.45 (1.80) | 5.30 (2.14) |
| Attention to Individual and Subgroups of Learners | 3.64 (1.36) | 2.61 (.96) |
| Lesson Rating | 3.68 (.60) | 3.92 (.53) |
As a reminder for the Quality of Evidence scoring dimension, participants received a score of 1-3 for the responses they gave to the assessment of the effectiveness of Lesson 1, Lesson 2, and the comparison between Lesson 1 and Lesson 2. These scores were then added together; thus, scores ranged from 3 to 9. The average score for the LLMT group (i.e., Mean = 6.45) was higher than the average MMC score (i.e., Mean = 5.30). An examination of the frequencies of the scores indicates that, while 38.5% of MMC participants received a score of 3 or 4 (a low composite score), none of the LLMT participants received a 3, and only 9.1% received a 4. This result indicates that a fairly high percentage of MMC participants demonstrated a lower level of assessing effectiveness of lessons; that is, they tended to focus on instructional strategies they used as teachers instead of examining whether students made progress toward the learning goals of the lesson. When some evidence related to students was mentioned by MMC participants, it was vague or general and mostly related to students’ overall engagement.
At the other end of the continuum, 27.3% of LLMT participants received the highest score of 9, demonstrating the ability to identify evidence of effectiveness directly linked to students’ specific mathematical content understandings and difficulties or to student engagement in math practices or to the use of specific mathematics academic language. Only 15.4% of MMC participants demonstrated this competence.
For the Attention to Individual or Subgroups of Learners rubric, participants received a score of 1-3 on each response that assessed the effectiveness of Lesson 1 and Lesson 2. These scores were added together; thus, scores ranged from 2 to 6. Overall, these scores tended to be lower than scores on the previous dimension. When comparing groups, the average score for the LLMT participants (Mean = 3.64) was higher than the MMC average score (Mean = 2.61).
Frequencies of these composite scores revealed that while 61.5% of MMC participants received a score of 2, only 18.2% of LLMT participants received this lowest possible score capturing both lesson responses. In addition, another 23.1% of MMC participants received a score of 3; thus, 84.6% of this group’s participants did not attend (or only minimally attended) to differences in progress toward the lesson learning goal by individual or subgroups of students.
Among the LLMT participants, 36.45% received a score of 3; thus, a total of 54.4% received a score of 2 or 3. At the other end of the continuum, while none of the MMC participants obtained a score of 6, 18.2% of LLMT participants did. These participants identified patterns of understanding and differences among students as they assessed the effectiveness of their lessons.
The lesson effectiveness ratings were virtually the same between the LLMT and MMC groups. These scores ranged from 3 to 5, with only one participant giving a rating of 2 to one of their lessons. Interestingly, when asked to provide a numerical rating of lesson effectiveness, most participants assigned a rating of 3 or 4. This result indicates that, overall, both groups saw room for improvement, but as the scores on the Focus and Quality of Evidence and Attention to Individual and Subgroups of Learners rubrics indicate, their assessments were based on different kinds of evidence.
Discussion and Conclusions
This study focused on an underexamined aspect of teacher competence — the ability to draw on evidence of student thinking and learning directly linked to lesson learning goals to assess the effectiveness of teaching. While prior research on the use of video in teacher preparation has provided support for its use as a tool to develop future teachers’ ability to attend to the details of student thinking, this study extended that work in two different ways. It asked whether video-enhanced experiences during teacher preparation support future competence once teachers enter the profession. It also developed a new measure to capture such competence and two scoring rubrics that define key skills within that competence.
Findings highlight that different teachers thought differently about their lessons when asked whether they were effective. Some relied mainly on instructional strategies they used and on general impressions about students’ overall engagement or ability to perform tasks correctly, whereas others attended to the details of their students’ thinking and difficulties and mapped those onto expected learning trajectories. These differences are striking in that participants were all first-year teachers and one can imagine quite different paths in their future development.
Overall, as a group, teachers received lower scores on the Attention to Individual or Subgroups of Learners rubric than on the Focus and Quality of Evidence rubric, possibly indicating that attending to individual students’ thinking and understanding is a skill that needs time to develop and is not prevalent in novice teachers.
Limited in scope by the small sample, this study is to be considered exploratory. It provides initial support for including video-enhanced experiences during teacher preparation that expose future teachers to detailed analyses of student thinking and to opportunities to develop evidence-based practices for reasoning about teaching and learning. Participants in the video-enhanced course on average outperformed participants in the control group on both the focus and quality of the evidence they drew upon, as well as the attention to individual or subgroups of learners.
Although written cases and analyses of student work samples would achieve similar goals as video analyses, images of classroom lessons provide unique opportunities for novice teachers to see in action how more experienced colleagues make space for student thinking to become visible, probe student thinking to move learning forward, engage students in classroom discourse and learn about students’ individual ideas while they teach. These opportunities facilitate teachers’ adoption of student-centered practices in their classrooms (Santagata & Yeh, 2014; Kiemer, Gröschner, Pehmer, & Seidel, 2014; van Es & Sun, 2015) while also developing student-centered dispositions and habits of reflection that place student thinking at the forefront (Mohr & Santagata, 2015; Santagata, 2010; Santagata & Guarino, 2011; Sherin & van Es, 2009).
Existing research provides support for the use of video to develop such classroom and reflection practices during teacher preparation. Few studies have examined the long-term impact of video-enhanced analyses during teacher preparation on future teacher practices; thus, this study’s findings contribute meaningfully to the literature.
Future work could include a larger sample of participants, which would afford more detailed statistical analyses. We could then examine whether the group differences are significant. We could utilize multivariate regression techniques to investigate relations of teacher learning outcomes with methods group participation. Teacher preparation programs are constantly struggling to include a multitude of competencies in their curricula; using these methods in future studies could help us understand whether spending time on these skills is warranted.
Future work could also refine the measure to make sure it fully captures teachers’ reasoning about effectiveness in teaching. Different teachers may have interpreted the survey questions differently and thought various degrees of depth were expected from their responses. A better insight into teachers’ reasoning about their daily effectiveness could be achieved through semistructured interviews.
Alternatively, if studies were focused on a larger sample of participants where surveys are necessary, teachers’ responses to survey questions could be supplemented by annotated samples of their students’ work. These would elucidate both insights into tasks teachers design to monitor student progress toward learning goals and teachers’ abilities to attend to details of student thinking that extend beyond right or wrong answers. The revised survey could also be complemented by additional questions that require teachers to assess the effectiveness of a given videotaped teaching episode with accompanying student assessment materials. This approach would allow for standardization of the representations used by teachers to demonstrate their reflection practices.
References
Bartell, T. G., Webel, C., Bowen, B., & Dyson, N. (2013). Prospective teacher learning: Recognizing evidence of conceptual understanding. Journal of Mathematics Teacher Education, 16(1), 57-79.
Blomberg, G., Renkl, A., Sherin, M. G., Borko, H., & Seidel, T. (2013). Five research-based heuristics for using video in preservice teacher education. Journal for Educational Research Online, 5(1), 90.
Borko, H., Jacobs, J., Eiteljorg, E., & Pittman, M. E. (2008). Video as a tool for fostering productive discussions in mathematics professional development. Teaching and Teacher Education, 24(2), 417-436.
Brophy, J. (2003). Using video in teacher education. New York, NY: Elsevier, Inc.
Carpenter, T. P., Fennema, E., Franke, M. L., Levi, L., & Empson, S. B. (1999). Children’s mathematics: Cognitively guided instruction. Portsmouth, NH: Heinemann.
Carpenter, T. P., Hiebert, J., Fennema, E., Fuson, K. C., Wearne, D., & Murray, H. (1997). Making sense: Teaching and learning mathematics with understanding. Portsmouth, NH: Heinemann.
Common Core State Standards Initiative. (2010). Common core state standards for mathematics. Retrieved from http://www.corestandards.org/assets/CCSSI_Math%20Standards.pdf
Empson, S. B., & Levi, L. (2011). Extending children’s mathematics: Fractions and decimals. Mathematics Education, 27(4), 403-434.
Gaudin, C., & Chaliès, S. (2015). Video viewing in teacher education and professional development: A literature review. Educational Research Review, 16, 41-67.
Greeno, J. G., Collins, A. M., & Resnick, L. B. (1996). Cognition and learning. In D. C. Berliner & R. C. Calfee (Eds.), Handbook of Educational Psychology (pp. 15-46). New York, NY: Simon & Schuster Macmillan.
Hatch, T., & Grossman, P. (2009). Learning to look beyond the boundaries of representation: Using technology to examine teaching (Overview for a digital exhibition: Learning from the practice of teaching). Journal of Teacher Education, 60(1), 70-85.
Hiebert, J., Morris, A. K., Berk, D., & Jansen, A. (2007). Preparing teachers to learn from teaching. Journal of Teacher Education, 58(1), 47-61.
Jacobs, V. R., Lamb, L. L., & Philipp, R. A. (2010). Professional noticing of children’s mathematical thinking. Journal for Research in Mathematics Education, 41(2), 169-202.
Jacobs, V. R., Lamb, L. L. C., Philipp, R. A., & Schappelle, B. P. (2011). Deciding how to respond on the basis of children’s understandings. In M. Sherin, V. Jacobs, & R. Philipp (Eds.), Mathematics teacher noticing: Seeing through teachers’ eyes (pp. 97-116). New York, NY: Routledge.
Jansen, A., & Spitzer, S. M. (2009). Prospective middle school mathematics teachers’ reflective thinking skills: Descriptions of their students’ thinking and interpretations of their teaching. Journal of Mathematics Teacher Education, 12(2), 133-151.
Kersting, N., Givvin, K., Thompson, B., Santagata, R., & Stigler, J. (2012). Measuring usable knowledge: Teachers’ analyses of mathematics classroom videos predict teaching quality and student learning. American Education Research Journal, 49(3), 568-589.
Kiemer, K., Gröschner, A., Pehmer, A. K., & Seidel, T. (2014). Teacher learning and student outcomes in the context of classroom discourse. Findings from a video-based teacher professional development programme. Form@ re, 14(2), 51.
Krammer, K., Hugener, I., Frommelt, M., der Maur, G. F. A., & Biaggi, S. (2015). Case-based learning in initial teacher education: Assessing the benefits and challenges of working with student videos and other teachers’ videos. Orbis Scholae, 2, 119-137.
Lampert, M., & Ball, D. L. (1998). Teaching, multimedia, and mathematics: Investigations of real practice. New York, NY: Teachers College Press.
Mohr, S., & Santagata, R. (2015). Changes in beliefs about teaching and learning during teacher preparation: The impact of a video-enhanced math methods course. Orbis Scholae, 9(2), 103-117.
Piaget, J. (1952). The origins of intelligence in children (Vol. 8, No. 5, pp. 18-1952). New York, NY: International Universities Press.
Santagata, R. (2009). Designing video-based professional development for mathematics teachers in low-performing schools. Journal of Teacher Education, 60(1), 38-51.
Santagata, R. (2010). From Teacher noticing to a framework for analyzing and improving classroom lessons. In M. Sherin, R. Phillip, & V. Jacobs (Eds.), Mathematics teacher noticing: Seeing through teachers’ eyes. New York, NY: Routledge.
Santagata, R., & Angelici, G. (2010). Studying the impact of the Lesson Analysis Framework on preservice teachers’ ability to reflect on videos of classroom teaching. Journal of Teacher Education, 61(4), 339-349.
Santagata, R., Gallimore, R., & Stigler, J. W. (2005). The use of videos for teacher education and professional development: Past experiences and future directions. In C. Vrasidas & G.V. Glass (Eds.), Current perspectives on applied information technologies (Vol. 2): Preparing teachers to teach with technology (pp. 151-167). Greenwich, CT: Information Age Publishing.
Santagata, R., & Guarino, J. (2011). Using video to teach future teachers to learn from teaching. ZDM The International Journal of Mathematics Education, 43(1), 133-145.
Santagata, R., Zannoni, C., & Stigler. (2007). The role of lesson analysis in preservice teacher education: An empirical investigation of teacher learning from a virtual video-based field experience. Journal of Mathematics Teacher Education, 10(2), 123-140.
Santagata, R., & Yeh, C. (2014). Learning to teach mathematics and to analyze teaching effectiveness: Evidence from a video- and practice-based approach. Journal of Mathematics Teacher Education, 17, 491-514.
Santagata, R., Yeh, C., & Mercado, J. (in press). Preparing teachers for career-long learning: Findings from the learning to learn from mathematics teaching project. The Journal of the Learning Sciences.
Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sensemaking in mathematics. In D. Grouws (Ed.), Handbook for research on mathematics teaching and learning (pp. 334-370). New York, NY: MacMillan.
Schoenfeld, A.H. (2017). Uses of video in understanding and improving mathematical thinking and teaching. Journal of Mathematics Teacher Education, 20(5), 415-432.
Seago, N. (2004). Using video as an object of inquiry for mathematics teaching and learning. In J. Brophy (Ed.), Using video in teacher education (pp. 259–286). New York, NY: Elsevier, Inc.
Sherin, M. G. (2004). New perspectives on the role of video in teacher education. Advances in Research on Teaching, 10, 1-28.
Sherin, M. G., & van Es, E. A. (2009). Effects of video club participation on teachers’ professional vision. Journal of Teacher Education, 60(1), 20-37.
Stockero, S. L. (2008). Using a video-based curriculum to develop a reflective stance in prospective mathematics teachers. Journal of Mathematics Teaching Education, 11(5), 373-394.
Stürmer, K., Seidel, T., & Schäfer, S. (2013). Changes in professional vision in the context of practice. Gruppendynamik und Organisationsberatung, 44(3), 339-355.
Sun, J., & van Es, E. A. (2015). An exploratory study of the influence that analyzing teaching has on preservice teachers’ classroom practice. Journal of Teacher Education, 66(3), 201-214.
Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2010). Elementary and middle school mathematics: Teaching developmentally. Boston, MA: Allyn & Bacon.
van Es, E. A., & Sherin, M. G. (2002). Learning to notice: Scaffolding new teachers’ interpretations of classroom interactions. Journal of Technology and Teacher Education, 10(4), 571-595.
van Es, E. A., & Sherin, M. G. (2010). The influence of video clubs on teachers’ thinking and practice. Journal of Mathematics Teacher Education, 13(2), 155-176.
Yeh, C., & Santagata, R. (2015). Preservice teachers’ learning to generate evidence-based hypotheses about the impact of mathematics teaching on learning. Journal of Teacher Education, 66(1), 21-34.
![]()