A key responsibility of mathematics teacher education is to empower prospective teachers as they cultivate their own problem solving abilities. Such abilities include not only solving mathematical problems but also providing mathematical explanations and justifications. Mathematics teacher educators must support prospective teachers as they foster these types of environments for their own students (Li, 2013). In recognition of this responsibility, three mathematics teacher educators (the research team), each at different universities, decided to engage prospective teachers in The Virtual Field Sequence (VFS). The VFS prepared prospective teachers to mentor elementary students online as the children worked on nonroutine Problems of the Week (PoW) through the Math Forum.
The online environment of the VFS and the Math Forum’s PoW allowed us and our prospective teachers to work collaboratively with mathematics teacher educators, teachers, and elementary school students across different parts of the United States. We began to think about the prospective teachers’ development in their mathematical explanations and justifications as a result of their participation in the VFS and the mentoring experience. The current research project examined the following question: How did participation in the VFS and online mentoring of elementary students affect the prospective teachers’ ability to explain solutions to mathematical problems?
This question parallels previous research in teacher education that first focuses on internalizing prospective teachers’ own mathematical problem solving abilities before creating these types of environments for students (see Cohen, 2011; Levasseur & Cuoco, 2003; Stevens et. al., 2007; Rathouz, 2009). Prospective teachers’ abilities to find solutions and communicate explanations to nonroutine problems were analyzed before, during, and after they went through the VFS modules and completed asynchronous mentoring of elementary students’ solutions to nonroutine challenge problems.
Background
Since the early nineties, researchers have agreed that students need to focus on the related mathematical practices or mathematical processes (National Council of Teachers of Mathematics, 2000), mathematical habits of mind (Cuoco, Goldenberg, & Mark, 2010; Mark, Cuoco, Goldenberg, & Sword, 2010), and more recently, the eight Standards for Mathematical Practice (SMPs; Common Core State Standards [CCSS] Initiative , 2010).
Two common features of desirable mathematical practices in the context of school classrooms have emerged from all of the descriptions and explanations (Li, 2013):
- Learners should be engaged in “productive and habitual ways of thinking and doing mathematics.”
- “Productive and habitual ways of thinking and doing mathematics” is something that all mathematical learners (not just mathematicians) should be doing. (p. 68)
The most current educational reform movement, the CCSS Initiative for mathematics, describes these practices as the SMPs. The CCSS include content standards for grades K-12 that describe what mathematics content should be taught at various grade levels, as well as the following eight SMPs (CCSSI, 2010) that describe the practices and processes through which students engage with mathematics:
- Make sense of problems and persevere in solving them, which involves students’, “explaining to themselves the meaning of a problem and looking for entry points to its solution.” (p. 6)
- Reason abstractly and quantitatively, including a student making sense of quantities and their relationships in problem situations and being able to contextualize and decontextualize the problem situation.
- Construct viable arguments and critique the reasoning of others, or a student communicating to others, plausible mathematical arguments that take into account the problem context.
- Model with mathematics, including a student identifying “important quantities in a practical situation and mapping their relationships using such tools as diagrams, two-way tables, graphs, flowcharts and formulas.” (p. 7)
- Use appropriate tools strategically, including a student considering the available tools when solving a mathematical problem.
- Attend to precision, including a student trying to communicate precisely through “clear definitions in discussion with others and in their own reasoning.” (p. 7)
- Look for and make use of structure, including a student looking closely to discern a pattern or structure.
- Look for and express regularity in repeated reasoning, including a student noticing if calculations are repeated, and looking both for general methods and for shortcuts.
When we were thinking about ways to study growth in the prospective teachers’ mathematical explanations, we saw distinct parallels between the Math Forum’s problem-specific rubric and the eight SMPs described in mathematics education reform documents. Using the Math Forum’s problem-specific rubric while tying it to corresponding elements of the SMPs would give us more ways to articulate the analysis of the prospective teachers’ solutions and explanations. The development and use of a coding scheme that ties the Math Forum rubric elements to components of the SMPs is further described in subsequent sections of this paper.
The literature contains little mathematics education research on teacher preparation experiences that engage prospective teachers in developing mathematical explanations in an online learning environment. Despite this paucity of research, interest in online distance education has grown exponentially in mathematics teacher education (Borba & Llinares, 2012). This interest is influenced by the fact that 85.5 % of higher education institutions offer some form of online learning, for example, entirely online courses or blended courses (Allen & Seaman, 2013).
Specific to the field of teacher education, 30% of higher education institutions offer completely online education-related degrees (teaching credentials and graduate degrees; Allen & Seaman, 2008). The influx of online and blended learning environments makes the study of prospective teachers’ development of mathematical justifications in online as well as offline learning environments imperative. The current study focused on prospective teachers’ development of mathematical explanations in online learning environments. The research question was as follows: “Do prospective teachers improve in development of their own mathematical explanations of their solutions to nonroutine challenge problems when they engage in a virtual learning experience?”
We sought to analyze improvements in mathematical explanations using the corresponding components of SMPs. In situations where we observed improvement in the prospective teachers’ mathematical solutions, we looked to identify what specifically about the explanations had improved. To describe and examine this improvement, we started with a problem-specific rubric developed by the Math Forum as a way to think about the type of growth we might see in prospective teachers’ solutions.
The rubric allows for assessment of both the problem solving and the communication aspects of a student’s submission. While this rubric allows for the evaluation of elementary students’ ability to write explanations, it also allows researchers to analyze prospective teachers’ written explanations. By focusing on problem solving and communication, researchers have a window into prospective teachers’ cognitive processes. For example, a prospective teacher’s interpretation and strategy for a problem, as evidenced through a written submission, shows how that teacher thought about the problem.
Ultimately, this study contributes to a better understanding of online teacher preparation experiences and how these experiences contribute to the development of prospective teachers’ mathematical explanations. The VFS and mentoring experience for the prospective teachers are described in the following section.
The Virtual Field Sequence
The VFS—previously the Online Mentoring Project—is a series of three online modules that were developed by the Math Forum (http://mathforum.org/pows) with support from the National Science Foundation. The modules prepare prospective teachers for the asynchronous mentoring of students’ submissions to nonroutine challenge problems. The modules are entirely online and accessible by anyone with an Internet connection, username, and password. The Math Forum has been involved in research on mathematics education at all levels for two decades.
To prepare the prospective teachers to be mentors, the VFS first gives them multiple opportunities to cultivate their own mathematical justification abilities. The prospective teachers must explain their own solutions to the challenge problems. Then, using the solution and explanation they developed in the first stage, the prospective teachers progress through modules and develop the skills necessary to mentor elementary students. Last, the prospective teachers read sample elementary students’ solutions and explanations, assess the students’ work and provide feedback, and practice mentoring elementary students as they improve their problem solutions. The experience culminates with the prospective teachers becoming mentors to actual elementary students engaged in the Math Forum’s PoW.
The approach used by the VFS reflects previous research of prospective teachers’ ability to explain solutions to mathematical problems (Rathouz, 2009). In order to focus on students’ mathematical thinking, rather than only the solution to a problem, prospective teachers are introduced to the concept of “Noticing and Wondering” (Hogan & Alejandre, 2010), both when they approach a mathematics problem and when they encounter student solutions to problems. Noticing and wondering emphasizes the importance of considering numerical values, measurable and countable attributes, numerical relationships, conditions, and constraints (Hogan & Alejandre, 2010). The modules also encourage prospective teachers to consider multiple strategies to solve a given problem and to acknowledge the value of a student’s strategy that may be different from their own.
The VFS has been implemented in various ways at different institutions (e.g., for different lengths of time, some work incorporated face to face) and illustrates the flexibility of the modules (Wall, Brown, & Selmer, 2014). The following descriptions, related examples, and approximate timelines are one way that the modules and live mentoring were adapted and implemented as a supplement in a face-to-face mathematics methods course.
VFS Module 1: 2 Weeks
With methods students, the first module of the VFS typically lasts 2 weeks. Prospective teachers notice elements of the Horsin’ Around problem (see Figure 1) and wonder about the scenario, considering possible solution strategies. After they solve the task, teachers share their solutions and accompanying explanations on an asynchronous discussion board (see Figure 1).

The following passage is an example of what a prospective teacher wrote in response to the prompt in Figure 1:
I noticed that he is going on a 50 mile journey, and we don’t know how long it took him. We know that he has a horse, but he only rides it half of the time. The horse goes much faster than he can walk (9 mph vs. 3.5 mph).
I wonder if he rides for 25 miles and walks for 25 miles, how long does it take him? I wonder how long he is traveling, because 50 miles is a long journey when you walk so slow. If he can go 9 miles in 1 hour and 3.5 miles in 1 hour, in 2 hours he could go 12.5 miles.
The discussion boards allow for multimodal submissions (e.g., image, video, written text, scanned work, and multimedia presentation), although the prospective teachers primarily submit either scanned, written, or typed work. The prospective teachers then analyze each other’s submissions. They are given prompts to think about as they question and respond to their peers. Next, prospective teachers read sample archived elementary students’ responses to the same problem. They write what they notice about the students’ work and note questions they might ask the students to help them improve their submission. In the last part of Module 1, the prospective teachers reflect on their problem-solving experience by answering the following questions.
- What does it mean to get better at noticing and wondering?
- What did you learn about noticing and wondering from reading other peoples’ work?
- How did different ways of noticing and wondering lead to different ways of thinking about the task?
- Were any of the solutions harder to mentor than others? Why?
- How did your peers’ feedback feel? Did you agree with their thinking?
The following is a sample of a prospective teacher’s reflections on the noticing and wondering process:
- I think I am already accustomed to noticing and wondering, I just don’t call it a name. Usually when I approach a problem I write down information that I think is significant (noticing), and then think about what the problem is saying and asking (wondering).
- I guess the difference is, my wondering is always about what the problem is asking for, not really what I personally wonder. I think it is great for slowing down the brain and focusing on what it is you are looking for. This slowing down and thinking will probably help students to not rush into problems. If they practice personal wonderings, students will probably find the problem more interesting.
- I think it is somewhat already a part of me from previous training. It is just like the writing process; however, even though we know there is a writing process out there, we take the tools from the process and make it our own process–what works for us!
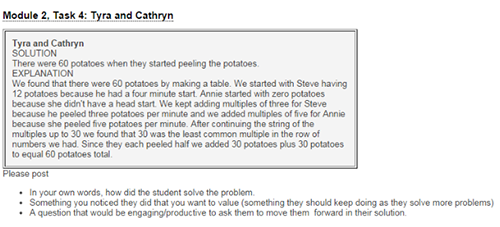
After students complete Module 1, they begin Module 2, which is similar and also lasts 2 weeks. Prospective teachers go through the same process, including writing their own solutions and explanations, reading and responding to peers’ submissions, and reading and responding to sample archived elementary students’ submissions to a new problem, Peeling Potatoes (see Figures 2 and 3). At the end of Module 2, the students reflect on their experience by answering the following questions.
- Which solutions did you find easiest to mentor? Which did you find hardest? Why?
- What is something you could do to prepare to mentor the students as you get ready to do live mentoring?

VFS Module 3: 2 Weeks
The third module introduces the Math Forum’s problem-specific rubric (see Appendix and refer to the explanation in the Methods section), and the prospective teachers apply it to archived elementary students’ submissions to the Horsin’ Around Problem, which was completed in Module 1. The rubric is divided into problem solving and communication categories. The problem solving category of the rubric is further divided into interpretation, strategy, and accuracy. The communication category of the rubric pertains to completeness, clarity, and reflection.
Module 3 also explores mentoring skills by having prospective teachers explore their own beliefs about effective mentoring, and they are introduced to the Math Forum’s guidelines for effective mentoring. Prospective teachers also practice mentoring other prospective teachers through further exploration of the Horsin’ Around Problem. The final Module 3 activities involve prospective teachers analyzing and critiquing sample mentor replies to elementary students’ submissions.
Live Mentoring: 3 Weeks
After they complete the three VFS modules, the prospective teachers engage in online mentoring of elementary students through the Math Forum’s PoW. (For more information on this topic refer to http://mathforum.org/problems_puzzles_ landing.html.) Each PoW cycle is 3 weeks. However, a new problem is posted every 2 weeks. Thus, elementary students might be revising a submission to a previous problem while beginning to solve a new one.
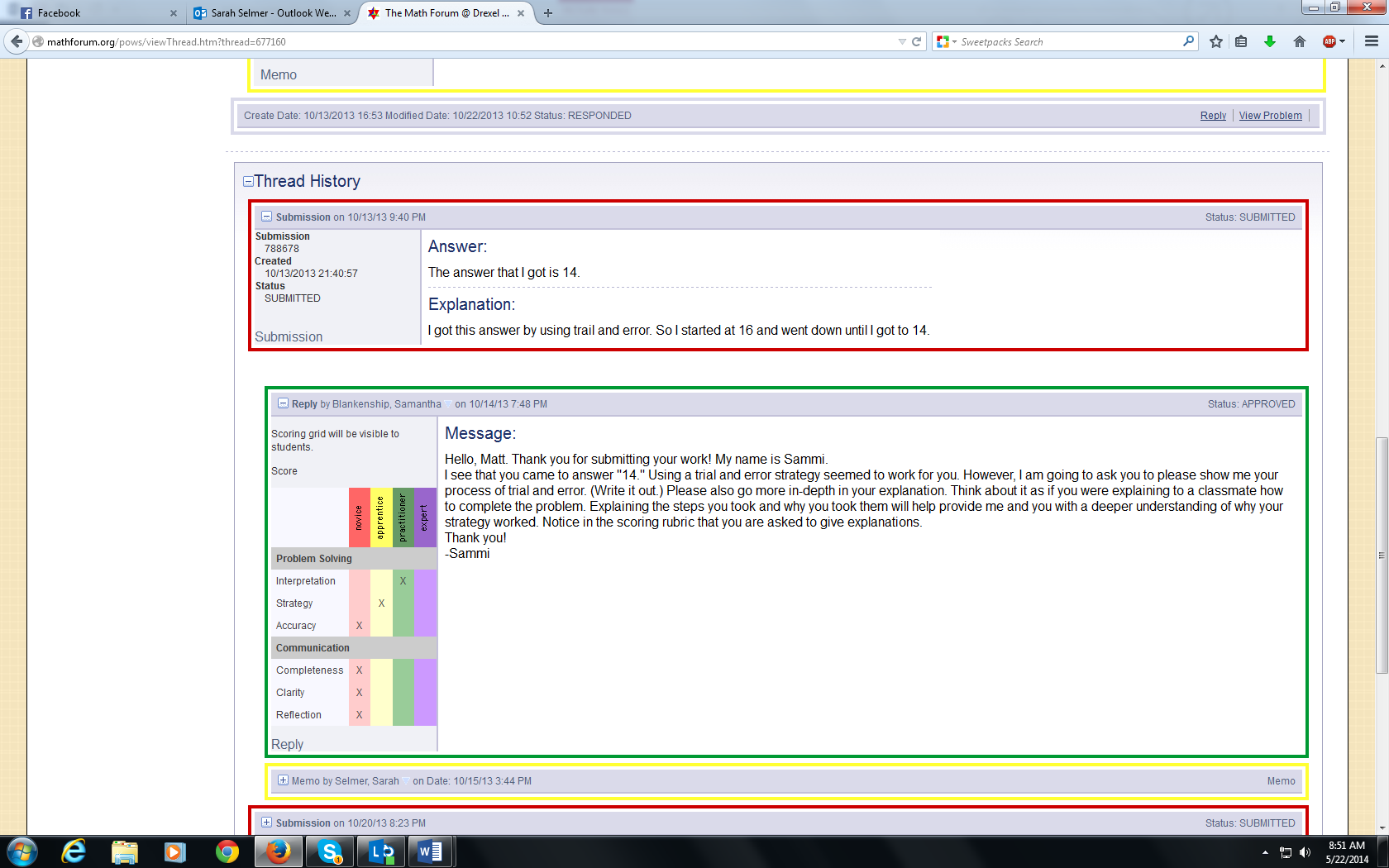
Throughout the 3 PoW weeks, elementary students respond to a challenge problem via a virtual learning platform where they are paired with a mentor (prospective teacher). The mentor helps the elementary student guide his or her learning in the areas of problem solving (interpretation, strategy, and accuracy) and communication (completeness, clarity, and reflection). In the virtual learning environment, there is a series of iterative, asynchronous communications between the elementary student, the prospective teacher, and the mathematics teacher educator. Figure 5 shows a sample of this series of communications for a problem (Figure 4) mentored during the fall 2013 semester. The elementary student’s submissions are boxed in red.
Using the rubric, the prospective teacher crafts a response to the elementary student (yellow box). The mathematics teacher educator must approve the response before it is sent to the elementary student. Thus, there is often an exchange between the prospective teacher and the mathematics teacher educator (green box) before the reply is sent to the elementary student. These students often revise the original submission (again in red) after receiving a response. The process continues throughout the 3 weeks (this continuation is not represented in Figure 5.). For a thorough description of prospective teachers engaged in the PoW experience as mentors, see De Young and Fung (2004).

Methods
Setting and Participants
The participants and settings spanned three different university campuses. Two of the universities are large state land grant universities, one in southern Appalachia and the other in the Mountain West. The third is a Midwestern 4-year regional university, which was historically a teachers’ college. At all three universities, mathematics education faculty members implemented the VFS, including live mentoring, within an elementary mathematics methods course taken as part of students’ professional education coursework one to two semesters prior to student teaching. At two of the institutions, the methods course is a face-to-face course; in the third, it is a blended online and face-to-face format.
Each of the three methods courses involved in the study enrolled 15-20 elementary prospective teachers for a total of 47 in the sample. The three instructors (the authors) implemented the VFS over approximately 7 weeks. Each instructor implemented the VFS and had prospective teachers progress through the VFS modules over similar time frames, and all prospective teachers completed each of three modules.
Data Sources
Throughout the semester, three data points were collected from the prospective teachers in the methods courses. Table 1 describes the collected data.
Table 1
Data Collection Points
| Data Point | When Collected | Target Grade Level | Problems Used |
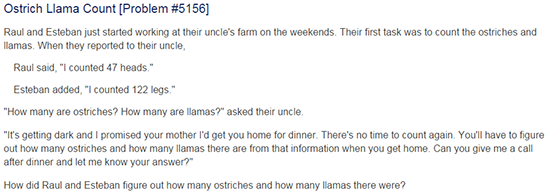
| Pre | First day of class, prior to any instruction related to PoW or VFS | 6th-8th | Ostrich and Llama (see Figure 6) |
| Mid | After completing the VFS, prior to live mentoring | 3rd-5th | Charlene Goes Shopping, Feathers and Fur, So You Think Your Teacher is Tough (see Figure 7) |
| Post | During the final exam, after completing the VFS, including the live mentoring | 6th-8th | Pumpkin Carving, Birthday Line Up (see Figure 8) |
At each point, the prospective elementary teachers composed responses to nonroutine challenge problems, and the instructors collected both their solutions and explanations. The first data point was collected prior to participation in the VFS modules, within the first week of class and before the prospective teachers had received any instruction on composing responses to such problems. At all three universities, the problem given at the first data point was the Ostrich and Llama problem as shown in Figure 6.
The second data point was collected approximately 7-10 weeks into the semester. After the prospective teachers had completed all modules of the VFS, except the live mentoring component, they composed their own responses to the nonroutine problem they would encounter while mentoring elementary students. The prospective teachers did not yet have access to rubrics or other materials related to the problem they were solving. However, they had worked with problem-specific rubrics for another problem, namely Horsin’ Around.
Because the prospective teachers did not all mentor elementary students during the same weeks, three different problems were used for this second data point. Figure 7 shows the three problems.
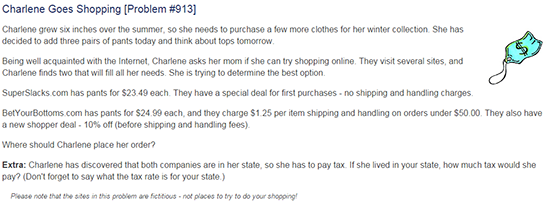


Figure 7. Problems of the Week for the second data point. (Copyright 2016, The Math Forum at NCTM. Reprinted with permission.)
Finally, the third data point was collected at the end of the semester as part of the students’ final exam. At this point, the prospective teachers had completed all of the VFS modules, including the mentoring of elementary students, and received feedback from their instructors on their mentoring. The three instructors chose a final nonroutine challenge problem for the prospective teachers to solve. The three universities used two different problems for this third data point. (See Figure 8).

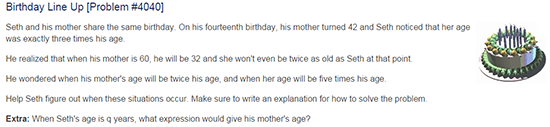
Figure 8. Problems of the Week for the last data point. (Copyright 2016, The Math Forum at NCTM. Reprinted with permission.)
After the methods course concluded, the three data points were reorganized to ensure participants’ anonymity and then analyzed using a coding scheme described in the next section.
Development of a Coding Scheme
A coding scheme was used to explore growth of the prospective teachers’ ability to respond to nonroutine challenge problems. The coding scheme was developed using the task-specific rubric developed by the Math Forum and the eight SMPs from the CCSS Initiative. After an initial discussion of the Math Forum rubric elements and the SMPs, we were able to map each rubric element to related SMPs (Table 2).
Table 2
Connecting Rubric Elements and Standards for Mathematical Practice
| Rubric Element | SMPs |
| Interpretation | 1, 2 |
| Strategy | 1, 2, 4, 5 |
| Accuracy | 6 |
| Completeness | 3 |
| Clarity | 3, 6 |
| Reflection | 1,7, 8 |
Part of the difficulty in studying experiences that develop prospective teachers’ engagement in mathematical practices is that fully developed mathematical practices are multifaceted: They can be practiced both externally (e.g., through students’ actions, written or verbal work) and internally (through students’ thoughts or internalized mathematical habits). Moreover, each practice is composed of multiple features (e.g., mathematical thinking habits, productive mathematical activities, and expertise and proficiencies in mathematics; Li, 2013), and the level of sophistication changes as students develop their mathematical thinking (CCSSI, 2010).
Due to the multifaceted nature of mathematical practices, Russell (2012) suggested that the practices be decomposed and parsed into smaller components in order to study student engagement. For this study, we decomposed and parsed the practices in two ways. First, we used a conceptual framework developed by Li (2013) that highlights the fundamental features of mathematical practices to be cultivated in learners. These features are broad and span all the practices. Second, we looked at each practice and considered components of that particular practice in the context of the rubric elements.
First Coding Scheme Iteration. Li (2013) developed a conceptual framework that parses mathematical practices as a whole into the following three features: (a) behavioral engagement and commitment, or the active working on mathematical problems; (b) development and employment of knowledge, skills, and strategies; and (c) internalization and habitualization, or the internal, natural, consistent use of mathematical practices. This study focused on prospective teachers’ behavioral engagement and commitment as one component of students’ engagement in mathematical practices.
In order to look at teachers’ behavioral engagement and commitment, we asked whether prospective teachers were doing the following:
- Actively working on mathematical tasks and activities, analyzing problem situations, engaging in thinking and reasoning processes, making conjectures and argumentations, and carrying out numerical computations and algebraic manipulations;
- Constantly reflecting on their progress, asking whether their mathematics makes sense, and making necessary adjustments for improvement; and
- Remaining committed and persistent until the completion of the tasks and the resolution of the problems. (Li, 2013)
These measures of engagement in mathematical practices match well with the experiences of prospective teachers as they progress through the VFS modules. It was, therefore, feasible to study whether the prospective teachers showed growth in components of behavioral engagement and commitment because of their participation in the VFS. Figure 9 highlights this initial decomposing of the practices.

Second Coding Scheme Iteration. The second way we decomposed and parsed the practices further emphasize components of individual practices. We turned to guiding documents for the Common Core State Standards in Mathematics (CCSSI, 2010), which describe the SMPs in detail, and each SMP was broken down into its components. For example, four components of the first SMP relate directly to this study:
- Students are “explaining to themselves the meaning of a problem and looking for entry points to its solution” (CCSSI, 2010, p. 6);
- Students “make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt” (CCSSI, 2010, p. 6);
- Students are making sense of problems and persevering in solving them when they reflect on the reasonableness of their solutions; and
- Students “check their answers to problems using a different method, and they continually ask themselves, ‘Does this make sense?’” (CCSSI, 2010, p. 6).
This process of breaking apart practices was done for each of the eight SMPs. Selected identified components of the SMPs were linked directly to the language and usage of the rubric.
Final Coding Scheme. We focused the final analysis on the components of SMPs 1, 2, 3 and 6 that closely paralleled the rubric element descriptions. The first element of the rubric, Interpretation, indicates that the student understands quantities given in the prompt, recognizes factors important to solving the problem that are not given in the prompt, and demonstrates understanding of the need to solve for the appropriate missing information. This element relates to SMP 1 (Make sense of problems and persevere in solving them). It indicates students should interpret what a problem is asking by using the given constraints, quantities relationships, and goals by, “explaining to themselves the meaning of a problem and looking for entry points to its solution” (CCSSI, 2010, p. 6). It also relates to SMP 2 (Reason abstractly and quantitatively), suggesting that students should reason quantitatively as they make sense of the given quantities in a problem situation as they analyze problem givens, constraints, relationships, and goals (CCSSI, 2010).
The second element of the rubric assesses whether the student picked a sound strategy to solve the problem, approached the problem systematically and logically, and achieved success through skill, not luck. This element also relates to the SMPs 1 and 2. Specifically, the first SMP mentions that students should show they have made sense of a problem by using the given information and finding a viable strategy to a solution (CCSSI, 2010). The second SMP encourages students to show they understand the quantities in a problem situation by using a viable strategy to find a solution.
Accuracy is the third element of the rubric, and it closely aligns to SMP 6 (Attend to precision). The rubric indicates that calculations that are included are accurate and contain no arithmetic mistakes, which is similar to the component of SMP 6, stating that students show attention to precision when they communicate accurately in their written solutions.
The next three rubric elements fall under the communication category, the first of which is Completeness, which relates to SMP 3 (Construct viable arguments and critique the reasoning of others). The rubric requires students to attempt to explain all of the steps taken to solve the problem with enough detail for another student to understand. Written responses might include key calculations with supporting commentary, all guesses they made, how they tested them, how that helped them make their next guess, and how they know they have correctly solved the problem. We aligned this rubric element to the component of SMP 3 stating that students construct viable arguments when the arguments are detailed.
The second communication rubric element is Clarity, which asks students to attempt to make explanations readable by a peer. Students must also use level-appropriate notation and mathematics language, including units (e.g., pounds, weeks, or days). Last, students should show effort to use good formatting, spelling, grammar, and typing. Clarity matches SMP 3. Clarity also aligns with SMP 6, in that students attend to precision when their written solutions are communicated clearly to others.
The final rubric element is Reflection, suggesting that students communicate a deep understanding of the entire problem solving experience by discussing their strategy, the mathematics, or the overall experience. In SMP 1, students make sense of problems and persevere in solving them when they reflect on the reasonableness of their solution.
Each rubric element is scored at three levels: Novice, Apprentice, and Practitioner. For certain elements, other than accuracy, an Expert level was also available. To maintain consistency across elements, the Practitioner and Expert levels were combined into one level, At Least Practitioner.
Data Analysis
Two members of our research group tested the coding scheme by rating and discussing two randomly selected predata points. The purpose of this initial testing was to begin to establish group consistency and shared understandings of the coding scheme as well as to refine the scheme. The two researchers rated the data at each point of collection independently at the beginning of the semester, during the VFS experience, and at the end of the semester. They then met again after each data point was individually assessed.
If there was disagreement for any data point, then the rating was discussed and the researchers came to a consensus. This refinement process allowed for interrater agreement of 100% for the 117 problem solutions that were analyzed. The process also allowed for improved consistency in the scoring of each problem and data collection point. Once scores were calculated for the three problems, the percentage of students scoring at each level could be calculated and examined between the first and the second data point and again between the first and the final data point.
Results
The paragraphs that follow describe evidence of the prospective teachers’ growth as shown in the collected data points. Descending trends (pre-mid and pre-post) in the percentage of prospective teachers scoring at the Novice level are described and the related ascending trends (pre-mid and pre-post) in the percentage of prospective teachers scoring at Practitioner (or At Least Practitioner) level. These trends are then further explained specific to each coding category. The final results section confirms these findings based on tests of significance.
Descending and Related Ascending Trends in All Coding Elements
For each element, Table 3 provides the percentage of prospective teachers that scored within each level for each of the three data collection points. The time at which the largest percentage of items was scored at the Practitioner (or At Least Practitioner) level is bolded within the table.
Table 3
Percentages of Students Scoring at Each Level Throughout the Semester
| Level | Pre | Mid | Post |
| Interpretation SMPs: 1,2 | |||
| Novice | 8% | 0% | 2% |
| Apprentice | 13% | 28% | 22% |
| Practitioner | 79% | 72% | 76% |
| Strategy SMPs: 1,2 | |||
| Novice | 12% | 2% | 18% |
| Apprentice | 37% | 14% | 20% |
| At Least Practitioner | 52% | 84% | 61% |
| Accuracy SMP: 6 | |||
| Novice | 17% | 0% | 12% |
| Apprentice | 25% | 14% | 20% |
| Practitioner | 58% | 86% | 67% |
| Completeness SMP: 3 | |||
| Novice | 6% | 2% | 12% |
| Apprentice | 81% | 34% | 37% |
| At Least Practitioner | 14% | 64% | 51% |
| Clarity SMPs: 3,6 | |||
| Novice | 4% | 0% | 0% |
| Apprentice | 58% | 38% | 37% |
| At Least Practitioner | 39% | 62% | 63% |
| Reflection SMP: 1 | |||
| Novice | 77% | 64% | 59% |
| Apprentice | 23% | 28% | 35% |
| At Least Practitioner | 0% | 8% | 6% |
For all of the elements, the percentage of students who scored at the Novice level decreased from the pre- to the middata points. When comparing the pre- and postdata points, the percentage of students who scored at the Novice level decreased for the Interpretation (SMPs 1 and 2), Accuracy (SMP 6), Clarity (SMPs 3 and 6), and Reflection (SMP 1) elements. The percentage of students who scored Practitioner (or At Least Practitioner) level increased from pre- to middata point for all elements other than Interpretation. For the Clarity element, that number increased again to postdata point.
The elements with the most drastic changes were Completeness (SMP 3) and Clarity (SMPs 3 and 6). The percentage of prospective teachers scoring at the At Least Practitioner level in Completeness increased from 13% to 64% from the first to the second data points. While it decreased again before the final data point, 51% percent scored at the At Least Practitioner level by the end of the semester. For Clarity, the percentage of prospective teachers scoring at the At Least Practitioner level increased over the course of the semester, from 39% to 63%.
An example of a student demonstrating drastic growth in SMPs 3 and 6 started with a student’s solution to the first problem, the Ostrich Llama Count problem (see Figure 6) that read “Even though the numbers don’t work out perfectly, I think there are 23 ostriches and 24 llamas??” In this brief solution, the student’s work does not reveal strategy or exhibit accuracy. The student earned a score of Novice in all areas except for Clarity, which was scored as Apprentice based on its readability.
After completing the VFS, the student wrote a solution to the Charlene Goes Shopping problem (see Figure 7) that was nearly a page long. It included four items the student noticed, equations the student wrote, and explanations of how the equations were manipulated to determine how much Charlene would spend at each store. It ended with a summary of which store would be the best option and why. For this data point, the student earned Apprentice for Interpretation and At Least Practitioner for Strategy, Accuracy, Completeness and Clarity. The student was still at Novice for reflection since none was included.
At the end of the semester for the Pumpkin Carving problem (see Figure 8) the student continued to be complete and clear in the solution by including equations, explanations of how the equations were solved, and reflections that were not originally included in either the pre- or the middata points. The student earned Apprentice for Reflection and At Least Practitioner for all other elements.
Another student submitted a solution to the Ostrich Llama Count problem at the beginning of the semester that included errors in the system of equations the student wrote. Rather than solving the system, the student wrote “And so on…” On the rubric, the student earned Apprentice for all elements except Reflection, for which the student earned Novice. This same student wrote a solution to the middata point So You Think Your Teacher Is Tough problem (see Figure 7) that was more than a page long. The strategy the student used was a guess-and-check strategy, and in order to be complete, the student included a table with many different possibilities in order to find the correct answer. Midway through the table, the student wrote a note indicating a realization of something about the problem that was previously unclear, suggesting that the student was interpreting the problem correctly.
After a few more lines in the table, the student stopped to write a pattern that was emerging and, thus, began utilizing that pattern for the remainder of the table. For this data point, the student earned At Least Practitioner for all elements except Reflection, for which the student scored Apprentice, including one Reflection. This student maintained the same levels into the final data point as well. These drastic changes, especially between the first and second data points, and for some students over the course of the semester, were rewarding to see.
Tests for Significance
We then conducted tests for significance to see if significantly more prospective teachers scored at higher levels at the second data point versus the first data point, and then also between the final data point and the first data point. The following factors were taken into consideration when determining which statistical test to use. The data are bivariate and categorical, which would normally suggest the use of a chi-squared test. Because of the high incidence of low expected cell counts, the assumptions for the chi-squared test were not met. Additionally, the levels within the rubric were ordered, that is, Novice is below Apprentice, and so on.
The times at which the data were collected were also ordered; because of instructional intervention between the data collection points, we predicted that students would improve after the predata point. Thus, the optimal test was a doubly ordered test. Given these factors, the nonparametric Jonckheere-Terpstra test was appropriate (Higgins, 2004). Doubly ordered tests, such as the Jonckheere-Terpstra (JT) test, assume no difference between the number of prospective teachers scoring at each level between data points. They examine all possible permutations of prospective teachers scoring in the different levels and determine if the observed frequencies within each level are significantly better than other possible permutations.
Table 4 summarizes the results of each of the test statistics, including the Jonckheere-Terpstra statistic, the standardized statistic (Z) and the p-value. The test statistics and p-values indicate if there were significantly higher frequency of scores in higher levels in the latter data point as compared to the former data point, considering all possible permutations of frequencies at each level. In this sense, we were not looking at changes in frequencies in one level at a time. Instead, the test statistics indicated significance (or lack thereof) of movement of the number of students scoring in lower levels to higher levels between each data point.
Table 4
Test Statistics to Detect Significant Differences From Pre- to Mid- or From Pre- to Postdata Points
| Element | Pre-Mid comparisons | Pre-Post comparisons |
| Interpretation | JT = 12464.5 Z = 1.299 p = 0.102 | JT = 1598.5 Z = 2.514 p = .006* |
| Strategy | JT = 1728.5 Z = 3.495 p = .000* | JT = 1337.0 Z = 0.481 p = .3424 |
| Accuracy | JT = 1699.5 Z = 3.382 p = .000* | JT = 1403 Z = 1.017 p = .168 |
| Completeness | JT = 1961.5 Z = 5.111 p = .000* | JT = 1653.5 Z = 2.962 p = .001* |
| Clarity | JT = 1625.0 Z = 2.489 p = .008* | JT = 1608.0 Z = 2.597 p = .006* |
| Reflection | T = 1492.0 Z = 1.617 p = .056 | JT = 1518.0 Z = 2.045 p = .023* |
| *p < .05. | ||
The test statistics validate what we had observed in the percentage of prospective teachers scoring at each level. A comparison of the first and second data points showed that significantly more prospective teachers scored at higher levels at the middle of the semester than at the beginning of the semester (p < .05) for the elements of Strategy, Accuracy, Completeness, and Clarity. Significantly more students scored at higher levels at the end of the semester compared to the beginning of the semester (p < .05) for the elements of Interpretation, Completeness, Clarity and Reflection.
Prospective Teachers’ Growth
Results showed significant evidence of prospective teachers’ growth over the course of the semester, particularly between the first and second data points. This evidence is seen in both the descending trends (the percentage of prospective teachers scoring at the Novice level) and the related ascending trends (the percentage of prospective teachers scoring at Practitioner/At Least Practitioner level). These results indicate that VFS participation positively influenced the prospective teachers’ development of stronger responses to nonroutine problems. Further, the percentage of students scoring at the novice level decreasing throughout the semester in the Reflection section indicates the positive influence the live mentoring had on prospective teachers’ inclusion of reflective thoughts in the submissions.
The coding scheme used in this project tied elements of the Math Forum rubric to specific components of certain SMPs, specifically SMPs 1 (Make sense of problems and persevere in solving them), 2 (Reason abstractly and quantitatively), 3 (Construct viable arguments and critique the reasoning of others), and 6 (Attend to precision). Table 5 shows each rubric element and the related SMPs components. This established relationship allowed us to look more closely at the individual components of each SMP in the consideration of VFS modules and mentoring experience features that possibly influence improvement in the prospective teachers’ scores.
Table 5
Connecting Rubric Elements to Components of SMPs 1, 2, 3 and 6.
| Rubric Element | SMPs | Components of SMPs 1, 2, 3, & 6 |
| Interpretation | 1, 2 | SMP 1 Component: Students are “explaining to themselves the meaning of a problem and looking for entry points to its solution.” (CCSSI, 2010, p. 6). SMP 1 Component: Students “make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt.” (CCSSI, 2010, p. 6). SMP 2 Component: Students reason quantitatively as they make sense of the given quantities in a problem situation as they analyze problem givens, constraints, relationships, and goals (CCSSI, 2010). |
| Strategy | 1, 2 | SMP 1 Component: Students use the given information and to find a viable strategy to a solution (CCSSI, 2010). SMP 2 Component: Students understand the quantities in a problem situation by using a viable strategy to find a solution. Algebraic solution strategies represent abstract thinking (CCSSI, 2010). |
| Accuracy | 6 | SMP 6 Component: Students are attending to precision when they communicate accurately in their written solutions (CCSSI, 2010). |
| Completeness | 3 | SMP 3 Component: Students are constructing viable arguments when the arguments are detailed (CCSSI, 2010). |
| Clarity | 3, 6 | SMP 3 Component: Students are constructing viable arguments when the arguments are clear (CCSSI, 2010). SMP 6 Component: Students attend to precision when their written solutions are communicated clearly to others (CCSSI, 2010). |
| Reflection | 1 | SMP 1 Component: Students are making sense of problems and persevering in solving them when they reflect on the reasonableness of their solutions. SMP 1 Component: Students show elements of SMP 1 when they “check their answers to problems using a different method, and they continually ask themselves, “Does this make sense?” (CCSSI, 2010, p. 6) |
Components of SMP 1. Prospective teachers improved their ability to explain their solutions to mathematical problems, both through work in the VFS modules and through actual mentoring of elementary students in the Math Forum’s PoW. As they worked on the VFS problems, they also engaged in a number of SMP components that focus on making sense of a problem situation by recognizing important quantities and relationships between these quantities. These skills relate directly to components of SMP 1 and SMP 2. Components of the SMPs were identified and connected to the Interpretation, Strategy, and Reflection elements of the rubric (see Table 5).
Each of these rubric elements and connected SMP components had significantly more people scoring at higher levels at the second and third data collection points than they had at the beginning of the semester. Specifically, Interpretation (with 8% scoring Novice to 2% scoring Novice by the third data point) and Reflection (with 77% scoring Novice to 59% scoring Novice by the third data point) saw significant improvements by the third data point (p = .006 and p = .023, respectively). While Strategy saw a significant increase at the second data point (p = .000) with a jump from 52% to 84% scoring At Least Practitioner.
Specific to the VFS problem-solving experience, prospective teachers’ introduction to and use of the concept of “Noticing and Wondering” (Hogan & Alejandre, 2010) in the VFS may have helped positively shift the prospective teachers’ performance in these SMPs components. Instead of jumping directly to “What do you know?” (Ray, 2013, p. 49) and finding a problem solution, prospective teachers were asked to notice important quantities and the relationship between these quantities. They also worked to wonder strategically as a segue or transition to finding a strategy. Teacher candidates might wonder if they had seen another problem similar to the one they were working on, wonder about what they are trying to figure out, think about patterns, try guessing, and so forth.
During the live mentoring experience, the prospective teachers used this same strategy with their elementary students to push them forward. They asked questions that redirected students back to the initial problem scenario instead of asking questions related to an incorrect solution. They asked, “What do you notice about the problem?” If a student already noticed the important mathematical quantities and relationships, the prospective teacher guided the students toward a viable strategy. Noticing and Wondering routines are examples of important habits of mind that reinforce prospective teacher development and engagment in SMP components.
Particular to the Reflection rubric element and related SMP 1 components (see Table 5), significantly more prospective teachers (p = .023) scored higher in the Reflection element, above Novice at the end of the semester (41%) compared to the beginning (23%). However, no significant improvement occurred between the first and second data points. As the last data point was collected after the prospective teachers had mentored the elementary students, the results suggest that the mentoring impacted the prospective teachers’ reflective practices more than the other components of the VFS. Clearly, opportunities exist to improve the VFS to emphasize reflective prompts more heavily. For example, the directions regarding reflective practices during the VFS are open ended. Although the current exercise starts the reflective process for the prospective teachers, explicit reflective prompts (e.g., “reflect on the reasonableness of your solution”) would target this specific component of SMP 1.
Components of SMP 3 and SMP 6. Prospective teachers also developed their focus on written mathematical communication during the VFS and live mentoring. Through these communications, they engaged in three SMPs components that focus on students’ construction of viable arguments that are detailed (SMP 3), precise (SMP 6) and clear (SMP 3). The corresponding elements of the rubric were Accuracy, Completeness, and Clarity, and these components, in fact, were the three that showed the most significant growth (Accuracy pre-mid, p = .000, with an increase from 58% to 86% scoring At Least Practitioner. Completeness pre-mid , p = .000, and pre-post, p = .001, with the greatest increase going from 14% At Least Practitioner to 64% At Least Practitioner. Clarity pre-mid, p = .008, and pre-post, p = .006, with the greatest increase going from 39% At Least Practitioner to 63% At Least Practitioner).
As the design and implementation of the VFS were based on asynchronous written mathematical communication, the most improvement was, not surprisingly, seen in prospective teachers’ scores for the communication-related SMP components of Completeness and Clarity. The process of reading student and peer solutions and explanations in Modules 1, 2, and 3 of the VFS and during live mentoring helped the prospective teachers realize the value of being detailed, precise, and clear when writing their own responses to nonroutine problems. For example, if prospective teachers could not understand what students or peers did because responses lacked detail, they learned that being detailed, precise, and clear in their own responses is important. Ultimately, the use of the Math Forum rubric encouraged prospective teachers to improve their mathematical communication.
Gains between the first and the second data points were not carried through to the final data point. Clarity was the only rubric element that continued to grow throughout the semester, and reflection decreased to novice levels throughout the semester. However, the other elements peaked after participation in the VFS.
This result could have occurred for multiple reasons. One possibility is that the second data point was collected using the problem for which the prospective teachers were going to be mentoring elementary students’ solutions. This situation of working with actual students on the same problem would likely motivate prospective teachers to perform at their best for this data point, more so than for other data points.
In future research, capturing the final data collection point immediately after live mentoring may better gauge the impact of the live mentoring on the prospective teachers’ solutions. In this case, the final data point was collected during the final exam, at which time the students had other things to focus on in addition to one problem. The fact that students had other questions on the final exam to answer, the length of time between the live mentoring and the final data collection point, and the differing levels of motivation for the second and third data points might have contributed to the decrease in the percent of students scoring at higher levels in most elements of the rubric.
Finally, while all problems used in this study were a difficulty Level 2, the pre- and postdata points were targeted toward Grades 6-8 while the middata point problems were written for Grades 3-5. Because of the timing of the live mentoring, the problems for the middata point had to be different from those chosen for the first and last data points. This difference may explain why continued growth was not seen from the second data point to the final data point; however, the significant difference on four of the six elements from pre-post data points indicates improvement in those elements across problems of the same difficulty and grade levels. Further research can examine whether the timing of the final data point collection or the differing grade levels of the problems were reasons for the lack of growth from the mid to the final data points.
Implications and Challenges
Our results and related discussion provide the following implications for mathematics teacher educators:
- Mathematics teacher educators should engage prospective teachers in solving a variety of problems while modeling instructional strategies such as Noticing and Wondering (Hogan & Alejandre, 2010).
- Mathematics teacher educators should engage prospective teachers in analyzing student solutions to problems.
- Mathematics teacher educators should provide assessment tools for prospective teachers, allowing them to assess both their own and students’ mathematical thinking.
- Mathematics teacher educators should emphasize the importance of mathematical communication—both written and oral—with prospective teachers.
- Mathematics teacher educators should engage prospective teachers in work with actual students.
This paper described an entirely online learning experience that engages prospective teachers in these highlighted teaching considerations. An online format benefits both prospective teachers and elementary students by reducing in-the-moment pressure that too often occurs in face-to-face learning environments. The online format enables more thoughtful, complete, clear, and accurate responses to problem situations.
Additionally, as the VFS modules are accessible by anyone with an Internet connection, username, and password, access is simple and flexible. Teacher educators can leverage such experiences to better prepare instructors for similar situations in synchronous environments.
Our results also highlight challenges mathematics teacher educators might encounter implementing similar educational experiences. The primary challenges we identified involved technical issues and coordinating work with live students. For example, students may have difficulty with passwords or may not understand the written directions of a particular module. These challenges highlight the benefit of working with established programs, such as the Math Forum, because they provide insight and assistance with technical issues in support of their learning platform. Another challenge specific to the mentoring of elementary students is the lag time between communications between mathematics teacher educators, prospective teachers, and the elementary students. To address this lag, a live mentoring schedule was developed and implemented to emphasize the importance of all parties responding within 24 hours to any communication.
Future Considerations
This research examined and connected components of certain SMPs to components of other SMPs, specifically SMPs 1, 2, 3, and 6. Moreover, it connected components of SMPs 1, 2, 3, and 6 to a learning experience for prospective elementary teachers and elementary students. Future research needs to continue both to unpack components of individual SMPs and explore how individual components are integrated and developed both within and across SMPs in teacher preparation experiences.
Researchers must explore beneficial ways to sequence engagement in integrated components of SMPs, both for prospective teachers and for elementary students. This study explored written communication; future work will consider students’ engagement in individual and integrated components of SMPs through oral communication in mathematical justifications to nonroutine problems.
Researchers must also consider that SMPs are not developed in isolation from mathematical content. Although research continues in both of these arenas, additional efforts to look at the relationship between the content and standards for mathematical practices will continue to aid the development and understanding of how mathematics is taught and learned.
References
Allen, I., & Seaman, J. (2008). Staying the course: Online education 2008. Boston, MA: The Sloan Consortium.
Borba, M., & Llinares, S. (2012). Online mathematics teacher education: Overview of an emergent field of research. ZDM Mathematics Education, 44, 697-704. doi: 10.1007/s11858-012-0457-3
Cohen, A. (2011, October). Evoking effective mathematical practices. Slides presented at the Enacting the CCSSM Standards of Mathematical Practices Conference, Lincoln, NE. Retrieved from http://scimath.unl.edu/conferences/esmp2011/documents/Evoking%20Effective%20Mathematical%20Practices.pdf
Common Core State Standards Initiative. (2010). Mathematics standards. Retrieved from http://www.corestandards.org/Math/
Cuoco, A., Goldenberg, E. P., & Mark, J. (2010). Contemporary curriculum issues: Organizing a curriculum around mathematical habits of mind. Mathematics Teacher, 103(9), 682-688.
De Young, M., & Fung, M.G. (2004). Online mentoring with the Math Forum: A capstone experience for preservice K-8 teachers in a mathematics content problem-solving class. Contemporary Issues in Technology and Teacher Education, 4(3), 363-375. Retrieved from https://citejournal.org/volume-4/issue-3-04/current-practice/online-mentoring-with-the-math-forum-a-capstone-experience-for-preservice-k-8-teachers-in-a-mathematics-content-problem-solving-class/
Higgins, J. J. (2004). Introduction to modern nonparametric statistics. Pacific Grove, CA: Thomson, Brooks/Cole.
Hogan, M., & Alejandre, S. (2010). Problem solving: It has to begin with noticing and wondering. CMC ComMuniCator, 35(2), 31-33.
Levasseur, K., & Cuoco, A. (2003). Mathematical habits of mind. In H. L. Schoen (Ed.), Teaching mathematics through problem solving: Grade 6-12 (pp. 23-37). Reston, VA: National Council of Teachers of Mathematics.
Li, X. (2013). Conceptualizing and cultivating mathematical practices in school classrooms. Journal of Mathematics Education, 6(1), 60-73.
Mark, J., Cuoco, A., Goldenberg, P., & Sword, S. (2010). Developing mathematical habits of mind. Mathematics Teaching in the Middle School, 15(9). 505-509.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
Rathouz, M. M. (2009). Support preservice teachers’ reasoning and justification. Teaching Children Mathematics. 16(4), 214-221.
Ray, M. (2013). Powerful problem solving. Portsmouth, NH: Heinemann.
Russell, S. (2012). CCSSM: Keeping teaching and learning strong. Teaching Children Mathematics, 19(1), 50-56.
Stevens, G., Cuoco, A., Harvey, W., Matsuura, R., Rosenberg, S., & Sword, S. (2007, May). The impact of immersion in mathematics on teachers. Paper presented at the Mathematical Sciences Research Institute (MSRI), Berkeley, CA.
Wall, J., Brown, A., & Selmer, S. (2014). Elementary prospective teachers’ mathematical justifications through online mentoring modules. In M. Searson & M. Ochoa (Eds.), Proceedings of Society for Information Technology & Teacher Education International Conference 2014 (pp. 490-493). Chesapeake, VA: Association for the Advancement of Computing in Education.
Author Notes
Jennifer Wall
Northwest Missouri State University
email: [email protected]
Sarah Selmer
West Virginia University
email: [email protected]
Amy Bingham Brown
Utah State University
email: [email protected]
Appendix
Example of a Problem-specific Rubric From the VFS Module 3
![]()
