Building On and Extending Previous Work
In this paper we describe an approach that enabled students to reinvent their own definitions of limit of a sequence in a course that used interactive technology to learn mathematics. The work described here was informed by prior efforts to develop solid conceptual understanding of limit with the help of interactive movable bands (Cory & Garofalo, 2011; Roh, 2008; Swinyard, 2011; Swinyard & Larsen, 2012). It built on previous work demonstrating the usefulness of the framework of approximation, error, and error bound (Oehrtman, Swinyard, & Martin, 2014), and was based on materials developed by the CLEAR Calculus Instruction project (Oehrtman & Martin, 2014).
Researchers in the CLEAR Calculus project successfully implemented the approximation framework in two research settings: one where two students worked together to reinvent the definition of limit through guided inquiry (Oehrtman et al., 2014) and another in a classroom with 11 students, where the instructor was one of the members of the research and development team (Park, Martin, & Oehrtman, 2013).
We extended the experience to a classroom at a different university where the instructor was not part of the research and development team. As Moore (1995) pointed out, in education, generally, innovations are successful in the hands of the innovators, but usually the innovations are not successful when someone else tries them. To contribute to a professional knowledge base that stems from research and from practice, it is important to demonstrate that the innovative approaches are effective beyond the innovators.
This study also extended the work of Oehrtman and his colleagues in a different way. At the University of Delaware, as in many other universities, future mathematics teachers take calculus with students in engineering and science in large sections (sometimes over 80 students). In such settings it would be difficult to implement guided reinvention to help students develop a deep understanding of limit. Our approach was an innovative experience in that a technology course was used to develop deeper conceptual mathematical knowledge for prospective mathematics teachers. This course was geared for preservice teachers for secondary mathematics in their first year and was offered as an alternative to satisfy a technology requirement in their program, which they usually satisfy by taking a computer science course. Based on our experience, we suggest that future teachers can gain a deeper understanding of limit at a level that is not usually attained in regular calculus courses.
The Importance of Conceptual Understanding of Limit for Future Math Teachers
Limit is one of the unifying ideas in undergraduate mathematics. Central concepts in calculus and other courses depend on the limit concept: derivative at a point as the limit of quotients of increments, the slope of a tangent line as the limit of slopes of secant lines; the definite integral as the limit of Riemann sums; continuity of a function; Taylor series; and the differential in multivariate calculus. The idea of limit is behind approximation methods such as Newton-Raphson to find zeros of functions and Runge-Kutta for approximating solutions to differential equations.
The concept of limit is not at the horizon of the mathematical knowledge for teaching (Ball, Thames, & Phelps, 2008) that future teachers need but at the very core of this knowledge. Teachers need a good understanding of the concept of limit because it is related to important topics actually taught in high school. For instance, three of the classroom-based situations discussed in Mathematical Understanding for Secondary Teaching (Heid, Wilson, & Blume, 2015) are directly connected to limit, namely, construction of a tangent line, the area of a curvilinear region, and differentiation. The Common Core State Standards for Mathematics (Council of Chief State School Officers & National Governors Association Center for Best Practices, 2010) recommended the informal use of limits when studying the circumference and area of a circle and the volume of the cylinder and cone.
In spite of the importance of limit, textbooks often do not discuss the concept in depth. Instead, textbooks focus more on how to compute or find limits. For instance, in a widely used book, an informal definition of limit of a sequence is introduced based on the discussion of one monotonic sequence. Then, after showing the graphs of two more sequences, a formal definition, involving symbols such as ε and N, is introduced and illustrated with one example (Stewart, 2012, pp. 691-692). The connection between the two definitions is not made explicit.
Without a systematic connection to the unifying concepts, students form meanings for each of the concepts in a fragmented and disconnected way (e.g., derivative as the slope of the tangent line, definite integral as the area under the curve, etc.). By providing teachers with opportunities to delve deeper into the concept of limit, they will have a stronger foundation on which to form a coherent and unified vision of topics based on limit.
Students’ Difficulties With Limit Concepts
Difficulties With Limit Concepts Formed From Informal Experiences
Students’ difficulties with the concept of limit have been well documented (Fernandez, 2004; Jacobs, 2002; Oehrtman, 2008; Oehrtman et al., 2014). Among the misconceptions reported in the literature are the following:
- Limit is a boundary that cannot be reached.
- Limit is a boundary that can be reached but not surpassed.
- The limit is the last term in an infinite sequence.
- A limit is a number which eventually, theoretically can be reached.
- As n increases an gets closer and closer to its limit.
Difficulties With a Formal Definition of Limit
The modern definition of limit of a sequence is complex and took mathematicians many years to formulate in a precise way (Grabiner, 1983). A formal definition is as follows:
“A sequence {an} converges to l
(in symbols ![]() )
)
if for every ε > 0 there is a natural number N such that, for all natural numbers n, if n > N, then |an – l| < ε.”
(Spivak, 1973, p. 373).
The definition has several sources of difficulty, including the many symbols involved with different meanings, use of inequalities, and absolute value. Another is the use of universal and existential quantifiers and the order in which they are used (Oehrtman et al., 2014). The definition also inverts the natural way of thinking about functions and sequences, which is to consider elements in the domain first (Oehrtman et al., 2014). To use the definition, students must start with a given error bound and compare it to the error, which is computed using the image value, an. Next, students must revisit the domain and find an N such that for subsequent values of n the desired inequality is true.
Furthermore, students’ difficulties learning limit concepts stem not only from its complexity and richness, but also because “the cognitive aspects cannot be generated purely from the mathematical definition” (Cornu, 1991, p. 153). Indeed, research has documented that students who are given a formal limit definition may have great difficulty making sense of that definition (Tall, 1992; Williams, 1991).
Difficulties With an Informal Definition of Limit
A common alternative uses informal language to introduce the concept of limit for a sequence. For example, one textbook describes a convergent sequence with language such as “the terms of the sequence {an} approach L as n becomes large” (Stewart, 2012, p. 691), or “A sequence {an} has the limit L … if we can make the terms an as close to L as we like by taking n sufficiently large” (Stewart, 2012, p. 692).
Such approaches are fraught with problems. Oehrtman (2008) pointed out that such rephrasing neither provides appropriately structured activities nor underlying meaning. In follow-up interviews, Oehrtman found that students who were exposed to such language attached simpler meaning to limit terminology. For instance, nearly all students interpreted the modifiers arbitrarily and sufficiently as indicators of degree. To them, sufficiently small meant very small, and arbitrarily small meant very, very small (Oehrtman, 2008, p. 68).
Using the Framework of Approximations, Error, and Error Bounds
We used the approximation, error, error bound framework (Oehrtman et al., 2014) to guide the reinvention of a limit definition (for the sake of brevity, we refer to it as the “approximation framework” from this point forward). In the next section we describe the main features of the framework. Next, we give a brief rationale for its selection in this study.
Description of the Framework of Approximations, Error, and Error Bounds
In the approximation framework, the limit L of a sequence an is considered as an unknown value to be approximated. The sequence values an are used as approximations, and the errors are |L − an|. Using the framework, students think about approximations and bounds in two different ways. In the first way, domain is considered first. For a given n and its corresponding approximation an, an idea how close the approximation is to the actual value is needed (i.e., an error bound). Saying |L − an| < .01, or |L − an| < .0001 provides a sense of the accuracy of the approximation.
In the second way, the range is considered first. That is, students first give a level of tolerance ε and then find approximations for which the errors are bound by the given level of tolerance ε. In the case of convergent sequences, students are able to achieve any predetermined degree of accuracy ε using approximations an by taking values of n that are large enough. Considering the range first reflects more closely the formal definition (Oehrtman et al., 2014, p. 133). Historically, considerations about errors and error bounds led the way to the clarification and formalization of the limit concept (Grabiner, 1983).
Rationale
We chose to use the approximation framework for teaching students the concept of limit of a sequence for three reasons. First, approximation and error analyses are commonly used by students and also significantly influence their reasoning (Oehrtman et al., 2014, p. 133). Second, the approximation framework provides ways of conceptualizing limit of a sequence that parallel the more formal definition. This framework “leverages an isomorphism between the structure and logic of approximation ideas and formal aspects of limit definitions” (Oehrtman et al., 2014, p. 133). Third, other conceptual models for limit that are used for teaching (based on images of motion, magnification and local linearity), and terms such as arbitrarily small and sufficiently small quantities are not widely used by students and have not been shown to influence students’ reasoning significantly (Oehrtman et al., 2014).
Crucial Issues in the Use of This Framework
In the transition from informal to formal understanding of limit, Swinyard and Larsen (2012) identified two necessary cognitive shifts. First, students must shift from a domain-first perspective to a range-first perspective. Second, students must be able to encapsulate the dynamic infinite limiting process into a self-contained entity via the concept of arbitrary closeness to overcome the practical impossibility of completing an infinite process.
Examples and Nonexamples
The Importance of Examples
Psychologists have found that most natural human concept formation is based on examples and sometimes on a specific example (Medin, 1989). Students rely on special examples of mathematical concepts called prototypes (Pitta-Pantazi, Christou, & Zachariades, 2007). Every concept has a set of examples and a set of critical attributes. However, as Hershkowitz (1987) pointed out, although mathematically there may be no essential difference among examples, psychologically, there is—with prototypes playing a special role.
One way to define prototype is as “those category members to which subjects compare items when judging category membership” (Rosch & Mervis, 1975, p. 575). Usually, textbooks do not have a large variety of examples, and some students develop limited conceptions and use prototypes that are too restrictive. In the case of limit, students often form their concept of limit based on prototypes that include properties such as monotonicity that are not part of the concept of convergence.
Examples and Nonexamples of Convergent Sequences
In order for students to define a concept, they must build mental images of the concept through a rich set of examples and nonexamples. Research has documented the importance of examples and nonexamples in the development of concepts (Sowder, 1980). When learning a new concept, students progress through different levels of concept learning. In the first four levels, examples (rather than a definition) play a crucial role. Only at the last level do definitions play a role in developing the understanding of a concept (Sowder, 1980).
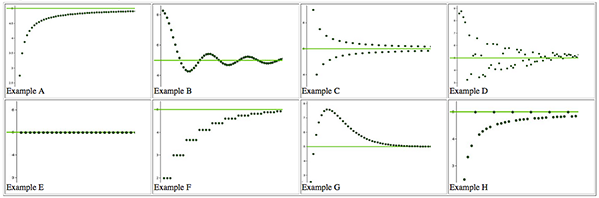
In this study, students generated a set of qualitatively distinct examples and nonexamples of sequence convergence prior to defining the limit of a sequence. Using by-hand and GeoGebra-based methods, students generated their own examples of sequences that converged or did not converge to 5. With GeoGebra, students initially used a formula with a continuous variable, so the instructor showed them how to graph sequences as discrete sets of points within the software. The instructor provided a handout of additional sequences from the examples developed by the CLEAR Calculus project, with eight examples of sequences that converged to 5 (Figure 1) and eight examples of sequences that did not converge to 5. These examples were also available during class through an interactive website (http://clearcalculus.okstate.edu/images/Guided%20Reinvention/Graphs%20-%20No%20Decoration/Sequence%20Graphs.html) and on posters on the walls of the classroom throughout the guided reinvention.
Nature and Components of Guided Reinvention
Iterative Cyclical Process
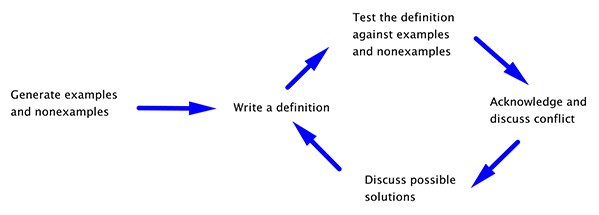
Oehrtman, Swinyard, Martin, Roh, and Hart-Weber (2011) described the reinvention as an iterative refinement. In this process, students write a definition, test it against a rich collection of examples and nonexamples, make problems with their definition explicit and share with their peers, discuss potential solutions, and revise their definition, starting the cycle again (Figure 2).
Roles of the Instructor as Facilitator
The fact that students work actively to reinvent the definition of limit does not make the instructor’s job easier. The instructor must act as a facilitator and provide guidance, scaffolding, and encouragement. The instructor/facilitator also helps make explicit problems that students may overlook. Four crucial roles of facilitators have been identified in previous work with pairs and multiple groups of students (Oehrtman et al., 2014; Park et al., 2013). These roles are depicted in Table 1.
Table 1
Guided Reinvention Instructors’ Roles (summarized from Park et al., 2013)
| Roles | Descriptions/Examples |
| Framing the task | Explicitly explaining what will or will not be part of the iterative refinement process (Park et al., 2013, p. 2). |
| Nudging students forward | Moving students forward in the iterative review process by explaining the procedure or asking students to focus on specific words and visuals in his examples, or in students’ own definitions (Park et al., 2013, p. 2). |
| Producing cognitive conflict | When students overlook problematic issues, “asking students to interpret their definition applied to a particular graphical example that their definition does not appropriately capture” (Park et al., 2013, p. 2) |
| Providing timely solutions | Providing a solution “after students wrestle with a problem for a significant time and have sufficient understanding of solution elements but remain unable to come to a satisfactory resolution” (Park et al., 2013, p. 2). |
Because this current study implemented the guided reinvention approach in a classroom setting, we summarize some of the facilitator roles that were highlighted in our implementation. Making these roles explicit so that the instructors/facilitators can optimize the guided experience for their students is important, “while preserving the students’ intellectual ownership of the process” (Park et al., 2013, p. 2).
When guiding the reinvention of limit, the instructor uses other students’ work and ideas in a systematic way (Park et al., 2013). For the reinvention activities, having several groups of three or four students enables the instructor to use the work or ideas of other students to produce cognitive conflict or provide solutions. For example, the instructor may use the work of one group to help another realize problems in their definition. Similarly, instead of providing a crucial element of a formal definition to students, the instructor can let other groups present their definitions and problems to the whole class and provide all students in the classroom with opportunities to adopt or reject others’ ideas (Park et al., 2013).
The Guided Reinvention
The Setting
The disciplined inquiry reported in this article can be described as action research (Sagor, 2000). The study was conducted by the instructor (first author Flores) mainly to assist in the improvement of learning mathematical concepts in depth in a technology course. The study also confirms and extends previous research (Oehrtman et al., 2011; Park et al., 2013) because the reinvention process took place in the setting of a technology course (rather than during clinical interviews with students or a calculus course) and was conducted by someone not part of the original design team.
All students who were enrolled in the course in spring 2015 participated in the study.
The instructor has ample experience in teaching calculus, in teaching methods for calculus with a conceptual emphasis, and in the use of technology to emphasize the development of concepts in the learning of mathematics. This was the first time the instructor conducted a process of reinvention of limit definition. Although only the first author served as instructor during the study, the pronoun “we” is used in this report because the second author participated actively in the development of the approach, analysis of data, and writing of the report.
Data sources for this study were the definitions of limit students wrote individually, small-group definitions posted on electronic forums, students discussions of their definitions in class, and observations of small group interactions. The data were analyzed using, on one hand, the approximation framework as a guide, noting to what extent students incorporated or not elements of the framework, and on the other, using the collection of examples of sequences that converged or not to 5, to see what examples were missing from the definitions and what nonexamples were included.
The guided reinventions were conducted in four sessions of 75 minutes during the ninth and 10th weeks of the spring 2015 semester as part of the course, Learning Mathematics with Technology (Flores, 2014)[a]. Nineteen students participated in the study, including 18 secondary mathematics education majors. Students worked in cooperative groups of three or four students.
The course contained several components that prepared students to face the challenging task of the guided reinvention and benefit from it: (a) students worked in cooperative groups; (b) they wrestled with challenging problems and tasks; (c) students communicated with each other; and (d) they used interactive technology to make sense of mathematical concepts and phenomena. From the beginning of the semester, students served as the audience for one another’s comments; they talked to and questioned one another and attempted to convince their peers.
Early in the semester, students realized this college course was not conventional—they would not be listening to polished lectures or taking notes but, instead, would be actively developing mathematical ideas. In every class, students were asked to focus their discourse on making sense of mathematical ideas and on using mathematical ideas sensibly when setting up and solving problems. Problem-based learning helps students realize that they can initiate, develop, and control their own learning (Allen, Donham, & Bernhardt, 2011).
As the name of the course indicates, the use of technology was an integral part of making sense of mathematics. Students used interactive and dynamical programs on a regular basis to explore and make sense of mathematical concepts. By the time of the guided reinvention, students had used GeoGebra for several weeks. They had experience in the software representing data, changing the scales on axes, zooming in an out of graphs, using sliders, and other similar tasks. During the reinvention process, each small group worked at a table with a 39-inch video monitor. Students displayed their examples and definitions on the screens so that everyone in their group as well as the instructor could see their work.
Next, we describe the reinvention experience in chronological order. In the first session, students spent considerable time generating examples and nonexamples.
First Two Attempts to Write a Definition
Toward the end of the first session on Day 1, after the examples and nonexamples had been generated and discussed, the instructor asked students to write individual definitions of a sequence that converged to 5. None of these included all essential components of a complete definition, even though 13 of the students had been taught the definition before.
Their initial definitions typically included dynamic terms such as get closer or approach. Also, as the following examples show, many include the same approaches, misconceptions, and misunderstandings reported in the research literature (Jacobs, 2002). For example, several definitions conveyed the idea that limit is a boundary that cannot be reached or surpassed.
- “A sequence sn converges to 5 as n → ∞ provided the terms grow closer to 5 consistently and gradually.”
- “A sequence sn converges to 5 as n → ∞ provided the sequence approaches, but does not move away from 5, and does so at a fast enough rate, i.e., each term must be closer to 5 than the previous one, and it must approach 5 quickly.”
- “A sequence sn converges to 5 as n → ∞ provided the sequence gets closer and closer to 5. It can also get through 5, for example y = 5 (it can also alternate around 5).”
- “A sequence sn converges to 5 as n → ∞ provided that as n increases, sn increasingly approaches 5, never surpassing 5, but eventually coming within .0001 of 5 or less.”
After writing their individual definitions, students worked in small cooperative groups to produce a first tentative small group definition. The groups’ first collaborative definitions did not differ significantly from individual definitions. Next, teams tested their definitions against examples and nonexamples and shared problems they were having with the whole group. Some definitions excluded examples that converged to 5 or included sequences that converged to a different number.
At the beginning of the second day, small groups wrote second tentative definitions and posted these on an electronic forum. At this point, the language and concepts used by different groups still varied widely, yet they also shared similar flaws, such as failing to reject nonexamples, or excluding sequences that converged to 5. Consider, for example, the following group-generated definition:
A sequence of ordered numbers converges to 5 if ultimately the approximations, Sn, have an error within a negligible error bound (i.e. there is no real number small enough to describe the distance from 5). Hence,
The example illustrates how the group conceptualized terms of the sequence as approximations. The group described the error (distance from 5) using the term negligible, for which they gave an explanation. The word ultimately was left without explanation.
Another team described the proximity of the terms of the sequence to the limit in the following manner: “A sequence converges to 5 if as n approaches infinity, |Sn – 5| is an infinitely small value.” The instructor mentioned to this team that the use of infinitesimals was not the approach used in their calculus courses, which is based on the real numbers, and encouraged the team to state their definition of limit in terms of real numbers.
In addition to asking questions to help students clarify their understanding, the instructor also asked students to clarify the meaning of vague words, avoid redundancies, and eliminate extraneous words. Moreover, the instructor suggested more precise mathematical terms to the whole group from time to time, provided suitable notations when needed, and reminded students of established notational conventions for sequences, such as using n instead of x for the independent variable. After groups revised their definitions, they tested their definitions against examples of sequences that either do or do not converge to the given number once again.
Introduction of the Approximation Framework
During the second session, the instructor provided timely solutions but still allowed students to have ownership of their definitions. To develop students’ understanding of the underlying structure of sequence convergence, the instructor introduced the approximation framework to students. Key terms from the framework—for instance, approximation, error, and error bound—were explained and illustrated with examples. Suitable notation was provided for the error. Students were asked to estimate error bounds for terms of sequences such as
![]()
The instructor made the reciprocal relationship between determining the error of a given approximation (n is given) and finding approximations within a given tolerance explicit. Epsilon bands were introduced as a way to identify terms of the sequence that fell within the selected error bound.
Students were made aware that they needed to shift their view to a range-first approach; that is, the error bound was given first, and students described for what terms of the sequence the error between the approximation and the limit was less than the error bound, rather than estimating an error bound for a given term of the sequence (as recommended in Oehrtman et al., 2014).
Interactive Movable Bands
The process of refining definitions as they were tested against examples and nonexamples was facilitated by the use of graphs of sequences with movable epsilon bands and N lines within GeoGebra. As students interacted with a movable epsilon band and an N line (Figure 3), they developed a better understanding of universal and existential quantifiers, as well as the roles of epsilon and N. This growth is reflected in the refinements of their limit definitions.
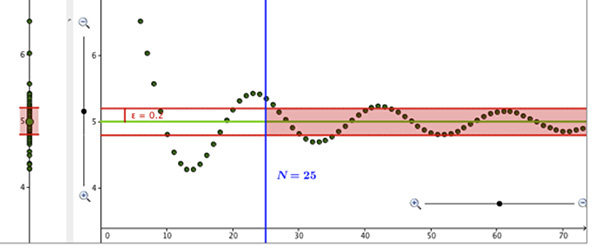
Figure 3. Epsilon band and movable N. From “Graphs with epsilon and N lines. Example B” originally published on the CLEAR Calculus website: http://clearcalculus.okstate.edu/images/Guided%20Reinvention/Graphs%20-%20with%20Epsilon%20and%20N%20Lines/Example_B.html. Copyright 2015 by M. Oehrtman. Reprinted with permission.
Students posted comments about the interactive examples and nonexamples. These postings show that the GeoGebra applet helped them clarify the meaning of convergence. Students stated that interacting with the epsilon band and the movable N line, zooming in (epsilon) and out (N), strengthened their understanding of limit. Consider, for instance, the following student comments about the epsilon band and the introduction of the movable N line:
Once we were looking at the ones with the epsilon band it was very helpful because it gave me a clear idea of what the definition should look like and what makes a sequence converge. The N activity was also helpful because it let us actually figure out how N plays into the definition.
Another student wrote,
The interactive examples and non examples were very helpful in determining a definition for convergence.… Using the visual graphs and taking the time to experiment with the values of epsilon and N allowed us to come up with a suitable definition more easily. Without this resource it would have been difficult to visualize the graph.
Several students noted that the interactive examples without the bands did not add much beyond what they could learn from static pictures on class handouts or wall posters in the classroom. However, others found it helpful to first have interactive examples without the band and N line. For the most part, students were able to use the online applets without problems, although a handful of students mentioned difficulties with zooming. Because they zoomed out too far, students experienced difficulty seeing all values. They were confused until students discussed the problem with each other in small groups.
Refining Their Definitions
On the third day, after the introduction of interactive examples (first without epsilon bands, next with bands, and finally with both epsilon bands and N lines), students posted another definition using informal language (for instance, “epsilon band” rather than “epsilon” to represent error bound).
The following example illustrates a definition that employs informal language that was suggested by the use of interactive GeoGebra applets:
A sequence converges to 5 if there are an infinite number of points within an epsilon band (with respect to 5) and a finite number of points outside said epsilon band, no matter how small epsilon is.
On the same day, teams received written feedback from peer teams regarding their definitions. Students were given explicit instructions (adapted from Oehrtman & Martin, 2014) regarding features of their feedback:
- Identify one example of a sequence that converges to 5 (A-H) that is incorrectly excluded by the other group’s definition. Explain why it is excluded. On the other hand, if all of the Examples (A-H) are correctly included by their definition, explain why.
- Identify one nonexample (1-8) of a sequence that does not converge to 5 that is incorrectly included by the other group’s definition. Explain why it is included. On the other hand, if all of the nonexamples (1-8) are correctly excluded by their definition, explain why.
- Describe what you like about the other group’s definition. What did they include in their definition that your group did not include? What did they leave out in their definition that your group did include? Is there something in their definition that you could use to improve your own? Explain.
Consider the following definition posted by one team during this round:
If the sequence is converging, the epsilon band will have an infinite amount of terms inside the range of the band, and only a finite number of terms outside of the epsilon band, no matter how small the range of the band is. If a sequence is non converging, there will be an epsilon band small enough to have only a finite number of terms inside the band and an infinite number of terms outside of it.
The following are peer comments regarding this definition. These comments suggest that providing feedback benefitted reviewers and reviewees alike.
- The provided definition does apply to all of the examples. For each series, the first value occurs when x = 1; thus, there will be a finite number, as opposed to an infinite number, of points outside any epsilon band. There will also be an infinite number of points inside the epsilon band for all examples, no matter how small the value of epsilon is.
- The provided definition does not apply for nonexamples 2 and 8 because there would be an infinite number of points within any epsilon band (no matter how small epsilon is) for both of these sequences. There would be an infinite number of points outside, but not a finite number inside, making these two examples not fit either the converging or non-converging definitions.
- From this definition we learned about a flaw in our definition, described in Part 2 above. Our definition was very similar to that of this group, in the sense that only a few words were different. We liked how they used the “range of the band” to describe the value of epsilon.
Toward a Formal Definition
In the fourth session, the instructor discussed student’s use of universal and existential quantifiers, using the language of the different groups to provide students with options for word choices in their own definitions. The instructor also noted that students were considering the error bound as a positive number, although they had not made it explicit in their definitions. He encouraged the teams to use more formal language such as epsilon rather than epsilon band. After this discussion, students revised their definitions for the last time and posted their final attempts.
Except for the use of 5 instead of a general L, the final definitions of three of the four groups were equivalent to formal definitions published in calculus textbooks. Consider, for instance, one team’s definition written in class without the benefit of outside sources: “A sequence converges to 5 if for any value of ε > 0 there exists some value, N, such that if n > N, then |Sn – 5| < ε.”
One of the teams was not able to post a definition that reflected the level of understanding that their small group’s discussion seemed to indicate. Of course, the ability (or inability) to describe concepts using symbolic notations is not necessarily indicative of the true understanding of students. In this case the instructor provided the small group with three examples of formal definitions of limit so that they could compare them to their own definition.
Conclusion
The evolving definitions illustrate the progress in students’ understanding. Successive definitions also reflect an increasing use of precise mathematical language. Thus, there is evidence that the reinvention of the definition activity was successful in helping students develop their understanding of limit and their ability to express the definition formally. Going through an iterative refinement process is particularly important for preservice teachers, because it provides a way of thinking about mathematical definitions and opportunities to reflect on their own thinking.
Having guided-reinvention experience can be specifically beneficial to preservice teachers, because it can affect their way of thinking about mathematics and learning mathematics. Through the guided reinvention activity, they may deepen their mathematical knowledge about important component of the formal definition of limit. They may also develop the understanding that what they learn in mathematics courses are not preexisting concepts but the products of human endeavor, in general.
Also, through the process of recognizing their problems with the definition and attempting to resolve them, they can experience learning mathematics independently and the importance of communicating about mathematics with others. The guided reinvention approach can also be used other with mathematical concepts with which students have difficulty due to dissonance with their existing schemas, such as the introduction of negative numbers or imaginary numbers. Without experiencing guided reinvention themselves as learners, the probability that preservice teachers adopt this student-centered and iterative approach or similar approaches would be quite small.
As previously mentioned, the instructor followed the guidelines for reinvention provided by the CLEAR Calculus project (Oehrtman & Martin, 2014), but also, following the advice given in the guidelines, made important adjustments based on students’ previous experiences with GeoGebra and their progress in class. It was possible to make adjustments while maintaining the fidelity of the implementation. The adjustments were made keeping in mind that the emphasis was on helping students reason critically as they worked through the iterative process rather than on trying to obtain a perfect definition from them.
Although students had 9 weeks of previous experience in the course grappling with challenging mathematics problems and tasks, this was the first time they had to work for an extended period of time on a definition. Several times during the process, teams became frustrated as they attempted to craft a written definition of the limit of a sequence as their own understanding was still evolving. An important role for the instructor was to recognize when pushing students further would be counterproductive.
The experience described here was a real teaching situation, where it was important to keep a balance between cognitive goals and affective goals. We did not want to push students so hard that they ended up hating the experience, even though they were successful in terms of learning the mathematics. The roles of the facilitator can help instructors be aware that in a challenging task such as reinventing the definition of limit, it is important to keep a balance between the different types of facilitator intervention. On one hand pointing out problematic issues that students have not made explicit or attended to is crucial, but on the other the facilitator needs to realize when to provide solutions after students have grappled enough with the issues, preferably in a way that preserves students’ ownership of the process (Oehrtman et al., 2014).
This study was not designed to claim generalizability of the results. The participants were all students enrolled in a specific course and not a random sample from a larger population. Other limitations are that the study was conducted in an especially favorable setting where the instructor had ample freedom to determine the content and pace of the course rather than having to cover predetermined topics. The reinvention experience also happened with students who had experienced for 9 weeks integrating the use technology as they grappled with challenging problems and tasks to develop their understanding of mathematics.
In addition to providing evidence that the guided reinvention of the definition of limit can be implemented successfully beyond the innovators, this experience also contributes to the professional knowledge base in other ways. As previously mentioned, the course used in this study satisfies a technology requirement rather than a mathematical one at our institution. In this article, we have provided an example of the type of deep mathematical knowledge that future teachers can gain through guided reinvention of formal definition of an important mathematical concept in such a course, and thus provided some evidence of the benefits an integrated math-technology course can bring to mathematics teacher preparation programs.
Note
[a] The course in which the activities were conducted was developed in part with funding from the National Science Foundation: S. A. Bernhardt, A. Flores, J. Park, H. Shipman (2012-2016), Integrated Science and Mathematics Education: A Model Course for Preservice Teachers (TUES Award No. 1140702).
References
Allen, D. H., Donham, R. S., & Bernhardt, S. A. (2011). Problem-based learning. New Directions for Teaching and Learning, 2011(128), 21-29.
Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389-407. doi:10.1177/0022487108324554
Cornu, B. (1991). Limits. In D. Tall (Ed.), Advanced mathematical thinking (pp. 153-166). Boston, MA: Kluwer.
Cory, B., & Garofalo, J. (2011). Using dynamic sketches to enhance preservice secondary mathematics teachers’ understanding of limits of sequences. Journal for Research in Mathematics Education, 42(1), 68-100.
Council of Chief State School Officers & National Governors Association Center for Best Practices (2010). Common core state standards—Mathematics. Retrieved from http://www.corestandards.org/Math/
Fernandez, E. (2004). The students’ take on the epsilon-delta definition of a limit. PRIMUS, 14(1), 43-54.
Flores, A. (2014). Integrating computers, science, and mathematics: A course for future mathematics teachers. In S. Zvacek, M. T. Restivo, J. Uhomoibhi, & M. Helfgert (Eds.), Proceedings of the 6th International Conference on Computer Supported Education (Vol. 2, pp. 246-251). Setúbal, Portugal: Scitepress. doi: 10.5220/0004942402460251
Grabiner, J. V. (1983). Who gave you the epsilon? Cauchy and the origins of rigorous calculus. American Mathematical Monthly, 90(3), 185-194.
Heid, M. K., Wilson, P. S., & Blume, G. W. (2015). Mathematical understanding for secondary teaching. Charlotte, NC: Information Age Publishing.
Hershkowitz, R. (1987). The acquisition of concepts and misconceptions in basic geometry—or when “a little learning is a dangerous thing.” In J. D. Novak (Ed.), Proceedings of the 2nd International Seminar on Misconceptions and Educational Strategies in Science and Mathematics (Vol. 3, pp. 238-251). Ithaca, NY: Cornell University.
Jacobs, S. (2002). Why is the limit concept so difficult for students? The AMATYC Review, 24(1), 25-34.
Medin, D. (1989). Concepts and conceptual structure. American Psychologist, 44(12), 1469-1481.
Moore, D. S. (1995). Teaching as a craft. MAA Focus, 15(2), 5-8.
Oehrtman, M. (2008). Layers of abstraction: Theory and design for the instruction of limit concepts. In M. P. Carlson & C. Rasmussen (Eds.), Making the connection: Research and teaching in undergraduate mathematics education (pp. 65-80). Washington, DC: Mathematical Association of America.
Oehrtman, M. & Martin, J. (2014). Calculus 2 labs: Lab 13 Constructing a formal definition. Retrieved from the CLEAR Calculus website: http://clearcalculus.okstate.edu/labs/calculus-2-labs#labs13-14
Oehrtman, M., Swinyard, C., & Martin, J. (2014). Problems and solutions in students’ reinvention of a definition for sequence convergence. Journal of Mathematical Behavior, 33, 131-148.
Oehrtman, M., Swinyard, C., Martin, J., Roh, K., & Hart-Weber, C. (2011, February). From intuition to rigor: Calculus students’ reinvention of the definition of sequence convergence. Paper presented at the 14th annual Conference on Research in Undergraduate Mathematics Education, Portland, OR.
Park, J., Martin, J., & Oehrtman, M. (2013). Scaling up reinvention: Developing a framework for instructor roles in the classroom. In S. Brown, G. Karakok, K. H. Roh, & M. Oehrtman (Eds.), Proceedings of the 16th Conference on Research in Undergraduate Mathematics Education (Vol. 2, pp. 613-618), Denver, CO.
Pitta-Pantazi, D., Christou, C., & Zachariades, T. (2007). Secondary school students’ levels of understanding in computing exponents. Journal of Mathematical Behavior, 26, 301-311.
Roh, K. H. (2008). Students’ images and their understanding of definitions of the limit of sequence. Educational Studies in Mathematics, 69, 217-233.
Rosch, E. & Mervis, C. B. (1975). Family resemblances: Studies in the internal structure of categories. Cognitive Psychology, 7, 578-605.
Sagor, R. (2000). Guiding school improvement with action research. Alexandria, VA: Association for Supervision and Curriculum Development.
Sowder, L. (1980). Concept and principle learning. In R. J. Shumway (Ed.), Research in mathematics education (pp. 244-285). Reston, VA: National Council of Teachers of Mathematics.
Spivak, M. (1973). Calculus. Menlo Park, CA: W. A Benjamin.
Stewart, J. (2012). Calculus: Early transcendentals (7th ed.). Belmont, CA: Brooks/Cole Cengage Learning.
Swinyard, C. (2011). Reinventing the formal definition of limit: The case of Amy & Mike. Journal of Mathematical Behavior, 30, 93-114.
Swinyard, C., & Larsen, S. (2012). What does it mean to understand the formal definition of limit?: Insights gained from engaging students in reinvention. Journal for Research in Mathematics Education, 43(4), 465-493.
Tall, D. (1992). The transition to advanced mathematical thinking: Functions, limits, infinity, and proof. In D. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 495–511). New York, NY: Macmillan.
Williams, S. R. (1991). Models of limit held by college calculus students. Journal for Research in Mathematics Education, 22(3), 219-236.
Author Notes
Alfinio Flores
University of Delaware
Email: [email protected]
Jungeun Park
University of Delaware
Email: [email protected]
![]()