In mathematics, representations are often used from the algebraic, geometric, numerical, and verbal registers to represent ideas, and moving between and within registers of representation is well recognized as an important part of mathematical understanding (Moore-Russo & Viglietti, 2012). In fact, when Duval (2006) defined a mathematical object (i.e., concept) as the commonality of all its associated registers of representation, he indicated that understanding of mathematical concepts can be achieved only through “a two-register synergy, and sometimes a three-register synergy” (p. 126) where synergy in this case can be perceived as simultaneous awareness of the various registers of representations associated with a mathematical concept.
Based on the assertion that understanding of mathematical concepts can be achieved only through simultaneous awareness of their associated representations, McGee and colleagues (McGee & Martinez-Planell, 2014; McGee & Moore-Russo, 2015) provided an operational framework by associating real comprehension of a mathematical object with the ability to fluidly move between its associated registers of representations which we consider multirepresentational fluency but refer to as fluency in this article.
Several authors found that promoting fluency across three registers of representation throughout topics of integration and differentiation significantly improved students’ problem solving abilities (McGee & Martinez-Planell, 2014; McGee & Moore-Russo, 2015). In recognition of the following premises, a test project at the University of Puerto Rico-Mayagüez (UPRM) was designed to explore whether this fluency approach, supported by digital resources, would improve the preparation of future mathematics teachers:
- Understanding the commonality of associated representations is a fundamental aspect of understanding mathematical concepts.
- Fluency and simultaneous awareness of registers of representations are key elements to recognizing the commonality of representations associated with concepts.
- A unifying philosophy based on premises 1 and 2 should be accessible to future teachers and may promote instructional practices more likely to facilitate students’ developing a deeper understanding of mathematics.
Theoretical Framework
From Kant’s (1929) and Piaget’s (1971, 1977) exploration of the epistemological relation between subject and object, Duval (2006) defined a mathematical object as the invariant of its possible representations. The paradox associated with this definition is that in contrast to other scientific fields, “the only way to have access to [mathematical ideas]… is using signs and semiotic representations” (p. 107). For example, a young child understands the number 2 by observing two stars, two fish, two hearts, and so forth, and understanding the commonality in these groupings (The Early Math Collaborative- Erikson Insititute, 2013).
Intraregister transformations, which involve moving between representations that occur within a single register without changing that which is being denoted (e.g., simplifying a series of equations from 2x – 4 = 6 to x – 2 = 3 to x = 5), were defined by Duval (2006) as treatments. Interregister transformations, which entail moving between representations that involve a change in register, even though no change occurs in that which is being denoted (e.g., passing from the symbolic representation y = 2x + 3 to the geometric representation of a line with intercept 3 and slope 2) were defined by Duval (2006) as conversions.
Duval (2006) stated that “the characteristic feature of mathematical activity is the simultaneous mobilization of at least two registers of representation” (p. 3). As simultaneous mobilization of representations can be difficult, the vast majority of learning modules and textbooks use an ordered sequence of semiotic registers when presenting a mathematical concept. In general, an ordered sequence of semiotic registers is best described as a semiotic chain with a linear order (Presmeg, 2006). (A semiotic chain is a sequence of signified-signifier pairs, where the signifier at one stage is contained in the signified of the next stage. The transformation from signified to signifier is either a treatment or a conversion.)
McGee and Martinez-Planell (2014) found that the ability to perform only the treatments and conversions associated with a semiotic chain is inconsistent with the synergy, or the simultaneous awareness, of semiotic registers that Duval associated with understanding of a mathematical concept. An example is shown in Figure 1, where the semiotic chain in Figure 1a has two associated conversions, each of which is represented by an arrow in the diagram: (a) the geometric register to the numerical register and (b) the numerical register to the symbolic register. Simultaneous awareness of these three registers would be associated with the ability to perform more than the two conversions in the semiotic chain and, conceivably, up to all six possible conversions as shown in Figure 1b.

Figure 1. A semiotic chain can evolve to a synergy of registers.
Hence, while mathematics educators may be unable to assess understanding of a mathematical concept directly, assessing the coordination or synergy of its associated semiotic registers (through the ability to perform associated treatments and conversions between them) should provide considerable insight into the conceptual understanding of the mathematical object at its core.
In a classroom context, consider a student that is accustomed to starting with a symbolic representation (a formula) performing a conversion to obtain the associated numerical representation (a table) and finally obtaining a graphical representation through ordered pairs on the Cartesian plane. The student would be accustomed to a unique semiotic chain: symbolic register → numeric register → geometric register.
The inability to perform conversions not included in this semiotic chain, such as geometric register → numeric register (graph to table) or numerical register → symbolic register (table to formula) would suggest that awareness of registers occurs sequentially as they appear in the semiotic chain. This inability would be considered inconsistent with a simultaneous awareness or a synergy of registers. However, if the student is able to pass seamlessly among the table, the graph, and the formula associated with the registers of representation, the student would be considered to have a simultaneous awareness or a synergy of registers.
Besides the institutional representations, those representations associated with textbooks and instructor presentations, students use spontaneous representations in mathematical situations, which are called transitional auxiliary representations (Hitt, Gonzalez, & Morasse, 2008). McGee and Martinez-Planell (2014) found that even when the numerical register has a natural role in presentations, textbooks sometimes assume that students can proceed to the symbolic register without the need to present the numerical register (tables or numerical expressions). In these circumstances, students are expected to access the numerical register as a transitional auxiliary representation without the need for its explicit presentation.
McGee and Martinez-Planell (2014) reported that (a) students are often unable to access the numerical register as a transitional auxiliary representation, in which cases it needs to be explicitly presented, and (b) students’ understanding can improve significantly when they are able to access the numerical register as an intermediary register when passing between registers of representation.
In this paper we use the term intermediary representations to describe representations that are spontaneously accessed by students performing conversions and are neither the source representation nor the target representation in the conversion. The nature of their use is similar to the use described for transitional auxiliary representations, in that they often refer to the spontaneous application of a third representation in order to perform conversions and solve problems. In this study, however, these spontaneously accessed representations may have been explicitly presented in instructional materials that the student had seen, which would make them institutional representations as well as intermediary representations. Correspondingly, we preferred not to use the term transitional auxiliary representation.
For this study we consider an intervention with preservice mathematics teachers, which adopted the fluency perspective on understanding of mathematical concepts and was facilitated by the application of digital resources to simultaneously represent semiotic registers of representation. The overarching idea that guided the study was to look at whether, and possibly how, such an intervention impacts preservice teachers. More, specifically, we asked the following three research questions.
- Does an intervention aligned with multirepresentational fluency impact how preservice teachers make sense of and solve mathematics problems involving conversions between registers? After the intervention, what differences are noted in preservice teachers’ solving of problems involving conversions between registers?
- How does an intervention aligned with multirepresentational fluency impact preservice teachers’ ideas of what it means for a student to understand a concept? In particular, does this intervention change how preservice teachers distinguish between understanding a concept and rote memorization of procedures involving the concept?
- How does an intervention aligned with multirepresentational fluency impact how preservice teachers plan to evaluate their students? In particular, will it better promote future teachers valuing understanding in the register flexibility sense, rather than valuing only rote memorization of mechanical processes?
Context
Setting
The National Assessment of Educational Progress (NAEP) is a standardized test with assessments in mathematics and other subject areas. An English language version is administered nationally in the United States, and a Spanish language version is administered in Puerto Rico. In 2003 and 2005, it served as a common metric for the United States and Puerto Rico by reporting three achievement levels for students: basic, competent and advanced. Table 1 (NAEP, 2006) presents results in mathematics for eighth graders in public schools for 2005. The results in 2003 were similar.
Table 1
Comparison of NAEP results in 2005 for the U.S. and Puerto Rico
Student Results Level | Puerto Rico | United States |
| Basic Level or better | 6% | 68% |
| Competent Level or better | 0% | 28% |
In 2007, the last year for which results are available for Puerto Rico, comparisons using this metric between the U.S. and Puerto Rico were no longer made. However, comparisons of the raw scores by subject area for eighth graders in the United States and Puerto Rico are shown in Figure 1 (Baxter, Ahmed, Sikali, Waits, Sloan, & Salvucci, 2007) and reflect little change from the raw scores in 2003 and 2005.
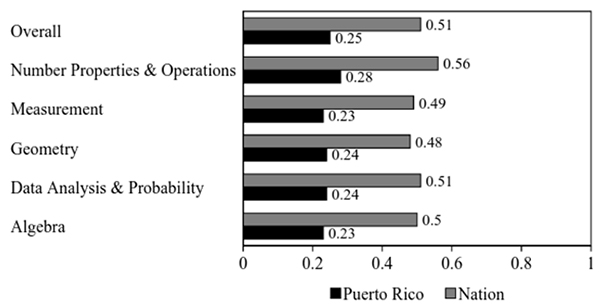
Figure 2. Comparison of NAEP Results in 2007 for the U.S. and Puerto Rico.
Internal online questionnaires have found that over two thirds of entering UPRM freshmen (n = 1,368) preferred an algorithmic approach (i.e., rote memorization of procedures) when solving mathematical problems. Data available from the diagnostic exam administered by the UPRM to entering freshmen reflected similar results as the data from the NAEP. In 2011, students received an average score of less than 10% on problems involving applied scenarios on the diagnostic exam administered by the UPRM, which would appear to reflect a powerful disassociation between mathematics and practical, real world situations. Hence, mathematics in Puerto Rico appears to favor rote memorization and to be disassociated from real world applications.
As no signs of improvement have been evident from 2003 to 2009 in the NAEP results in Puerto Rico, newly trained teachers entering the school systems in Puerto Rico do not seem to be making gains to improve student understanding of basic mathematics concepts. The continued superficial mathematical comprehension shown by students entering the UPRM would serve to call into question how deeply future teachers really understand many of the fundamental topics of mathematics.
Participants
Six future teachers were paid a stipend of $3,000 to participate in a program that would help their preparation for the certification exam. The program requirements were to attend a 3-hour orientation and then spend approximately 6 hours a week working with a variety of materials to help prepare for the teacher certification exam over the course of 6 months. The study participants all
- held bachelor’s degrees from a Puerto Rican college or university in a STEM field,
- had completed at least one semester of a supervised teaching practicum in a secondary school in Puerto Rico,
- had completed at least 9 hours of education courses,
- were expected to take the teacher certification examination within 6 months, and
- had GPAs above 3.0, with overall qualifications that made them likely to pass the certification exam based on similar qualifications in past years.
All future teachers who met these criteria and applied to participate in the program were accepted and became study participants. The experimental materials were embedded within a larger set of materials, all of which were collectively expected to prepare the study participants to become certified as secondary mathematics teachers in Puerto Rico.
Intervention
The intervention in the study involved both a 3-hour, kick-off orientation session and a 6-month independent preparation period. In this section the orientation session is described in more detail, then, the interactive, multiregister digital resources used for linear functions that supported the orientation session are described. Finally, we described the interactive, multiregister digital resources for exponential functions that were independently used by the study participants and that formed the basis for evaluating the results of the study.
The digital resources used by the study participants during the extended independent preparation actually encompassed most topics associated with precalculus mathematics, but this study’s scope was limited only to those related to linear functions (as used in the orientation session) and exponential functions (one of the many topics addressed by the digital resources during the individual preparation period).
The following activities were used in the orientation session to introduce students to a multirepresentational fluency approach to understanding. The study participants were initially presented with basic tenets of semiotics through a brief lecture that introduced (a) conversions and treatments, as movements between and within, respectively, registers of representations; (b) multirepresentational fluency, as the ability to move fluidly between and within registers of representation, and (c) understanding, as identifying the commonality of all representations. Henceforth, the term fluency will be used for multirepresentational fluency in this article.
We divided the study participants into pairs and challenged them to create lessons that might promote fluency and understanding of mathematical concepts by recognizing the commonality of their representations. The pairs of students then shared and discussed their lessons with the entire group.
Next, we introduced the study participants to the interactive applets described in Figure 3 that allowed for simultaneous viewing of the verbal, numerical, graphical and algebraic representations of linear functions. These applets were produced with GeoGebra, a free software program with the capacity to dynamically present algebra, spreadsheets and geometry (http://www.geogebra.com). We explained how these GeoGebra applets could be used to support fluency with linear functions by simultaneously presenting representations from multiple registers in an interactive environment that allowed the participants to control and adjust the parameters associated with the real world scenario that was presented.
 a. Upon opening the web page containing the online materials, a simple interactive example of a linear relation is shown, the decrease in value of a machine.
a. Upon opening the web page containing the online materials, a simple interactive example of a linear relation is shown, the decrease in value of a machine. 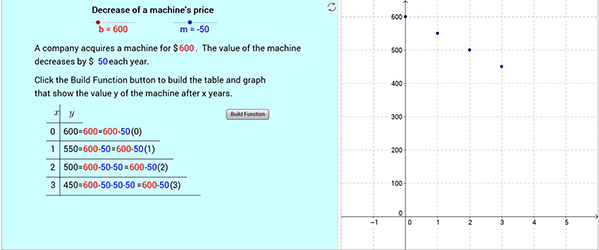 b. Using the interactive sliders, the values associated with the linear function can be altered. In this case, the initial price of the machine was changed to $600, and the value of decrease each year was set to $50. Then, when the “Build Function” button is clicked, the table and graph are populated with the values of the machine over the successive years.
b. Using the interactive sliders, the values associated with the linear function can be altered. In this case, the initial price of the machine was changed to $600, and the value of decrease each year was set to $50. Then, when the “Build Function” button is clicked, the table and graph are populated with the values of the machine over the successive years. 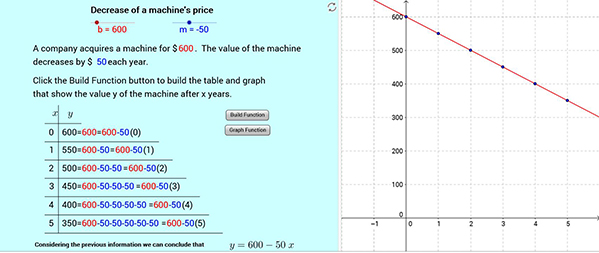 c. After completing the table, the formula and graph for the linear relation are shown. The output values in the table were written in a form to facilitate understanding of the resulting formula.
c. After completing the table, the formula and graph for the linear relation are shown. The output values in the table were written in a form to facilitate understanding of the resulting formula.
Figure 3. A GeoGebra applet to simultaneously present verbal, numerical, algebraic, and geometric representations associated with linear decay.
Then in pairs, the participants created a second round of technology-enhanced lessons that incorporated one of the GeoGebra applets as a digital resource to promote students’ fluency and understanding of linear functions. The orientation finished with a second round of sharing and feedback based on the new technology-enhanced lessons.
During the extended preparation period, the participants had access to and independently used similar digital resources on a variety of precalculus topics to prepare for the teacher certification exam. During this 6-month preparation period, the participants had access to a number of online GeoGebra applets that simultaneously showed representations from the verbal, numerical, graphical and symbolic registers in an interactive environment that allowed for parameter variations. When online quizzes showed that a participant repeatedly scored less than 80 percent on a topic, we would intervene to help this participant with individual tutoring.
An example of the digital resources that related to exponential functions can be seen in Figure 4 or accessed from the Math Tutorials website:
- http://kcm.nku.edu/tutorials_master_eng/fn_exp/ExponentialFunctionsGrow.html
- http://kcm.nku.edu/tutorials_master_eng/fn_exp/ExponentialFunctionsDecay.html
Many of the other topics, ranging from quadratic functions to trigonometric modeling, resembled those shown in Figures 3 and 4 and similarly concentrated on reinforcing this representation flexibility approach to understanding. However, they are not presented in this paper.
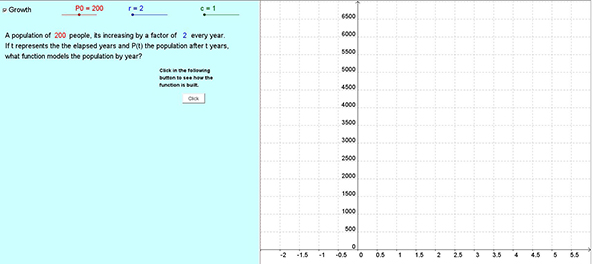
a. Upon opening the web page containing the online materials, a simple interactive example of an exponential relation is shown. 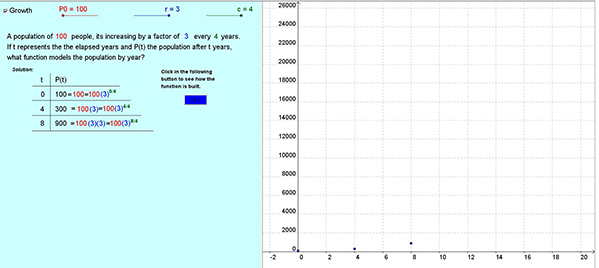
b. Using the interactive sliders, the values associated with the exponential function can be altered. In this case, the initial population was changed to 100 with the population tripling every 4 years. Then, as the button is clicked, the table is populated and the graph’s points are inserted for the number of people at 4-year intervals.
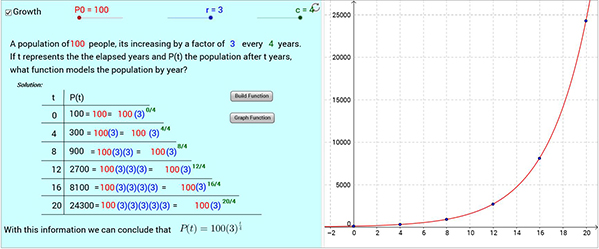 c. After completing the table, the formula and graph for the exponential relation are shown. The output values in the table were written in a form to facilitate understanding of the resulting formula.
c. After completing the table, the formula and graph for the exponential relation are shown. The output values in the table were written in a form to facilitate understanding of the resulting formula.
Figure 4. A GeoGebra applet associated with exponential growth.
Data Collection and Analysis
Overview
Data were collected from two sources for this study. The first involved observations of the six study participants during the orientation session. The second involved pre- and postintervention interviews with the study participants, which were conducted as follows: Upon being selected for the project and prior to any other activity, preintervention interviews were conducted with each participant. One to 2 weeks following the preintervention interview, a 3-hour orientation session was conducted for all study participants. It was designed to introduce them to conversions between registers of representations, fluency, and understanding mathematical concepts through the commonality of their associated representations. Observations of the study participants of the six preservice teachers were conducted during the orientation session.
Approximately a week after the orientation, students dedicated 6 months to individual preparation for the certification exam. This preparation included access to and use of the online quizzes and GeoGebra applets. Two to 3 weeks after completing the preparation, postintervention interviews were conducted with each study participant.
Observations of Participants at the Orientation Session
We (the lead author and a second professor, both of whom had worked in mathematics education at the UPRM for a combined total of 35 years) led the orientation session with the help of a graduate student who was also a certified teacher. While one of us was facilitating activities and discussions, the other observed and took notes on the study participants. We agreed to concentrate our observations on the following questions.
- How well did the study participants understand the fluency approach to understanding mathematics?
- To what extent was this perspective on understanding mathematical concepts new and novel for the study participants?
- How receptive were the participants to this perspective on mathematical understanding?
Direct inquiries risked prompting study participants to answer questions in a manner that they thought would most please their professors. Hence, gleaning information from general and small group discussions was preferred to one-on-one interviews with professors. The observing professor asked questions only to clarify study participants’ statements and did not attempt to direct the discussion in any way.
Interviews
To compare how participants engaged in solving problems before and after the intervention, the two interviews were semistructured and included questions involving similar scenarios. The lead author conducted the first round of interviews. The other professor conducted the second round of interviews. The postintervention interview consisted of slight variations of the questions from the first interview (e.g., different numbers).
The interviews began with mathematical tasks that participants talked through as they complete, then the interviews ended with more pedagogically focused questions that related to the tasks. Interview questions are provided in Appendix A. Both sets of interviews were recorded, and all lasted approximately 1 hour.
Both interviews focused on exponential growth and decay. While the intervention itself covered a range of precalculus topics, only the concept of exponential functions was selected as the focus topic of the interviews. Understanding exponential functions is required of high school preservice teachers, so theoretically, the study participants should have understood them reasonably well prior to the intervention. However, only 7% of high school students in Puerto Rico pass the AP exam for precalculus, and exponential functions is one of the topics with which they struggle the most. Correspondingly, we decided that exponential functions provided a good topic for capturing a preintervention to postintervention evolution of the capabilities and perspectives of future teachers.
Two important aspects were related to the interviews. The primary purpose of the first interview was to determine the preservice teachers’ understandings of exponential functions, where understanding was based on the idea of a synergy of registers as formulated by Duval (2006). Likewise, the degree to which a synergy of registers was attained was based on the ability of the participants to perform the following conversions. It should be noted that some of the more predictable, and hence easier, conversions were not included in the interview in order to allow a more comprehensive exploration of less common conversions. The conversions that were addressed included
- symbolic register to numerical register,
- numerical register to symbolic register,
- symbolic register to geometric register,
- verbal register to numerical register,
- verbal register to symbolic register,
- verbal register to geometric register, and
- symbolic register to verbal register.
After we assessed study participants’ knowledge of exponential functions, they discussed their perception of students’ understanding of exponential functions and how this understanding should be evaluated in the second interview. In addition to questions similar to those used during the preintervention interview, these additional interview questions (as translated from Spanish) were included as part of the postintervention interview:
- How do we know whether students understand a topic, as opposed to them memorizing a procedure?
- As teachers, how can we create presentations and evaluations to promote understanding over rote memorization?
- Did the GeoGebra materials alter your perspective on what it means to understand a concept? How?
- Did the GeoGebra materials alter your perspective on how teachers should write exam questions for students? How?
The two interviews were conducted by different individuals intentionally to minimize the association preservice teachers made between the two interviews. By minimizing the association between the interviews, the expectation was that the participants would be less likely to build on the prior interview but would respond to each interview in its own context. The interviews were analyzed through memo-writing, with general (followed by some preliminary axial) coding. The correctness of mathematical conversions that were requested in the interview were scored with a preestablished rubric, and statistical significance between pre- and postintervention scores were determined using a two-tailed Student’s t-test.
Results
Observations at the Orientation Session
The study participants appeared not only to understand but also enjoy the idea of a mathematical concept being based on capturing the commonality of associated representations. One participant described this approach as “mind blowing.” When asked why he would use this description, he replied that “he had always defined a mathematical idea first and then used representations to illustrate the idea. This was kind of the opposite.”
Another participant was asked how he had previously defined a mathematical concept. After some thought he indicated that he generally used a formula or a verbal description. The group discussed this strategy at length and concluded that, historically, they generally had used one representation to define a mathematical concept and others to illustrate it. They concluded that, while not incorrect, defining a concept using only one representation could be limiting, whereas looking for the commonality in various representations, in particular real world situations, was more likely to result in a deeper understanding of the concept. In general, the discussion demonstrated a mature philosophical perspective on this register flexibility approach to mathematics. While it appeared to be new to them, they seemed receptive to associating understanding with simultaneous access across registers of representation.
After the general discussion, the study participants divided into pairs to create lessons that simultaneously accessed various registers of representation in order to promote understanding of mathematical concepts. We were, in general, impressed with the thought processes that were generated by looking at concepts from this perspective. For example, Table 2 shows how one of the pairs organized the registers of representation they associated with the quantity one half.
Table 2
Examples of Registers of Representation Participants Generated for “One Half” During the Orientation
Numerical | 1/4, 2/4, 3/6, 4/8 … 50% |
| Verbal | Splitting an object into two equal parts Dividing n objects between two people, containers, places, etc. |
| Geometric | A geometrical shape divided into two parts with half shaded A geometrical shape divided into 2n parts with n parts shaded. A set of 2n objects with a marked subset of n objects. |
| Graphical | The number marked on number lines with different unit sizes. |
These representations produced a lively discussion about the difference between ½ as a number on the number line and as a fraction of a whole. The participants also felt that “splitting” and “dividing” in the verbal register should be changed to “the fraction of the whole that results from splitting or dividing” to keep the list “consistent.” As the other registers represented a number (or noun), they said, the verbal register must represent a noun as well and cannot represent an operation (or verb). Throughout these discussions, participants were seeking commonality, inconsistencies, and intuitive conversions between registers of representations. They seemed to relate well to this approach and to feel that it lent clarity to what it meant to understand mathematical concepts.
The session concluded with the presentation and a discussion of the GeoGebra applet for linear functions that was shown in Figure 3. One of the study participants commented that this use of technology was one of the best she had seen. When asked why, she said that in her student teaching, even when using only two representations, she had been frustrated when trying to change a parameter in a formula to show its effect in a graph. The nature of her work required the following sequence of events:
- The formula y = x2 was written on the blackboard.
- The graph of y = x2 was drawn on the blackboard and labelled with its formula.
- The initial formula was altered to y = 2x2 to show a vertical stretch.
- The graph of y = 2x2 was drawn on the axes and labeled with its formula.
- She ended up with labeled graphs for y = x2 and y = 2x2 on the same axes.
The frustrating aspect for her was that students often perceived this sequence as two different problems rather than the effect of altering or introducing a parameter of a single type of function. She felt that only real-time access to the table, graph, and formula when parameters in a situation are altered has the potential for students to associate the four representations as manifestations of the same phenomenon, and anything short of real-time access would result in separation of the representations into distinct phenomena by many students.
The group generally agreed that the value of these applets went well beyond convenience and entertainment. The participants’ comments and discussion suggested they felt the digital resources provided an educational opportunity that could not be replicated in a classroom environment without such resources.
Our summary observations of the orientation session included the following:
- All three of the preservice teacher pairs were able to produce registers of representation that included situational, numerical, graphical, and symbolic registers that would be associated with the same concept (see an example in Table 2). During the orientation session, the conversations, activities, and questions remained in the context of achieving understanding through commonality across registers of representation, and at no time did any participant revert to a single register approach to comprehension. All seemed consistent with comprehension of this fluency approach to understanding mathematics.
- Participants unanimously recognized that associating understanding with the commonality of various representations was a significant change from how they thought about mathematical concepts and how mathematical concepts are understood. Before this orientation, they typically defined a concept using an algebraic equation alone, then presented other representations in other registers as consequences of this definition. Simultaneously accessing various representations to define a concept was a significant ideational shift for the participants.
- Participants were enthusiastic and receptive to this approach to understanding. However, they were university students receiving a stipend, so they may have had a desire to please us. Therefore, their enthusiasm might not mirror pedagogical practices that they will ultimately implement in school classrooms.
Quantitative Results of Interviews
The interviews strived to capture how study participants’ understandings of the mathematical topic of exponential functions were impacted, where understanding of a concept was associated with the ability to perform conversions between registers of representation. As a synergy of registers should imply the ability to pass between all known registers associated with the same mathematical concept, particular attention was paid to participant’s ability to perform unaccustomed conversions between familiar registers of representation (McGee & Martinez-Planell, 2014; McGee & Moore-Russo, 2015).
Table 3 presents the average score as demonstrated in the interviews before and after the intervention for basic conversions associated with exponential functions. Most preservice teachers were able to perform conversions commonly found in school texts. The two least successful conversions on the preintervention interview were (a) from the numerical to symbolic register and (b) from the symbolic to verbal register. Preservice teachers who were unsuccessful in performing the conversion from the numerical register to symbolic register all believed that they had seen this conversion before. However, they all believed that it was uncommon and outside normal practice for exponential problems. None felt they had seen the conversion from the symbolic register to the verbal register prior to the preintervention interview, and only one was successful in performing this conversion.
While basic problem solving skills (or at least the familiar conversions) for exponential functions were relatively solid for the study participants in the first interview, as was expected for a well-prepared group of preservice mathematics teachers, these skills left room for improvement. Struggles with unfamiliar conversions in the preintervention interview indicated that different representations of the same concept were often isolated from one another, and simultaneous awareness of semiotic registers was probably not present. In the postintervention interviews, participants performed all of the requested conversions associated with the same concept, both common and uncommon.
Qualitative Results of Interviews
Preservice Teachers’ Understanding of Exponential Functions. The quantitative results shown in Table 3 indicate that from preintervention to postintervention, the participants’ abilities to solve problems with exponential functions improved in all seven conversions, and the improvement was statistically significantly (p < 0.05, based on a two-tailed Student’s t-test) in three out of seven conversions. More importantly, even when these preservice teachers could respond to a question correctly in the preintervention interview, often a considerable difference appeared in the way they responded after the intervention.
Table 3
Participant Scores on Questions Involving Conversions Between Registers
Conversion (related interview questions) | Preintervention Score | Postintervention Score |
Symbolic Register to Numerical Register (Q2,Q7) | 88 | 100 |
Numerical Register to Symbolic Register (Q1,Q6)* | 50 | 100 |
Symbolic Register to Geometric Register (Q2,Q7) | 88 | 100 |
Verbal Register to Numerical Register (Q4,Q9) | 88 | 100 |
Verbal Register to Geometric Register (Q4,Q9) | 88 | 100 |
Verbal Register to Symbolic Register (Q4,Q9)* | 67 | 100 |
Symbolic Register to Verbal Register (Q5,Q10)* | 12 | 100 |
| * p < 0.05 | ||
For example, Glenn was asked to respond to the following question both before and after the intervention: “If an initial population of 10 triples every 4 years, what is the formula for the exponential relation?” Figure 5 shows the preintervention and postintervention approaches Glenn used to solve the problem. (The questions changed slightly from the first to the second interview, so the table demonstrates the approach and not necessarily the precise calculations made.)
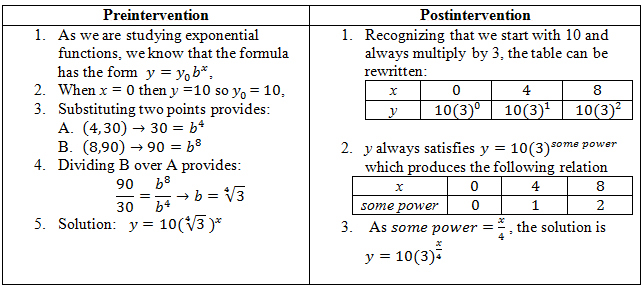
Figure 5. Glenn’s approaches to solving an interview problem before and after the intervention.
At the first postorientation meeting (approximately a week after the first interview), Glenn was asked to describe a situation that could be associated with the formula y = 10(∜3)x. He indicated that it was an exponential function with y0 = 10 and b = ∜3; however, he was unable to associate the formula with a population that triples every 4 years. Prior to the intervention, the process of converting a situation to a mathematical formula lost this fundamental aspect of the situation.
Postintervention, when asked to comment on the significance of y = 10(3)x/4, Glenn indicated that it was a function that started with 10 when x was 0, and then it tripled every time x increased by 4. Hence, converting the situation to a mathematical formula in this manner retained the information contained in the situation. When this loss or retention of information associated with the conversion of a situation to a formula was discussed with Glenn, he indicated that before the intervention, the idea of retaining information when expressing a situation mathematically had not occurred to him. After the intervention, he was aware of retaining the relation between different representations. Therefore, while the intervention did not affect his ability to solve the problem, it greatly changed his perspective on the relationship between the real world context and the mathematical representations.
This situation with Glenn was representative of that of the other study participants who responded correctly to the question in the preintervention interview. In that first interview, all of the participants used either y = y0bx or y = y0ekx
for the formula associated with the situation, and their work primarily consisted of finding the associated constants. When they were later presented with the formula that they had found, none were able to associate it with the situation. Hence, during the preintervention interview, expressing a situation from the real world as an algebraic equation resulted in a loss of information. Postintervention, all participants were able to move fluidly back and forth between the mathematical equation and the real world situation without loss of information.
Before the intervention, most of the study participants were able to perform the desired conversions. However, when converting situations, tables or graphs to an equation, all of them defaulted to using one of these equations y = y0bx or y = y0ekx, and the conversions tended to require significant work algebraically. Postintervention, all of the preservice teachers were still able to convert to an equation, but instead chose to (a) first convert a situation or graph to a table and (b) follow the postintervention strategy shown in Figure 5 to arrive at a formula with almost no algebraic manipulations.
Since simultaneous awareness of the different registers of representation for the same mathematical concept is associated with conceptual understanding (Duval 2006), another indication of preservice teachers’ underlying understanding is their ability to introduce voluntarily different representations for the same mathematical concept when convenient to do so (McGee & Martinez-Planell, 2014; McGee & Moore-Russo, 2015). Perhaps, the most compelling indication that this simultaneous awareness may have improved as a result of the intervention was the appearance of tables as intermediary representations.
Preintervention, tables were used exclusively as intermediary representations to construct graphs. Postintervention, tables were used over 90% of the time as intermediary representations to obtain a formula (See the pre- and postintervention work shown in Figure 5, for an example). Hence, preintervention only conversions involving a graph would include intermediary representations, which provides no evidence of awareness of other registers besides the source and target registers. Postintervention, almost every conversion that participants performed incorporated at least three of the four representations (geometric, numerical, symbolic, and verbal).
For example, when given a verbal representation and asked to find a formula postintervention, study participants invariably used a table as an intermediary representation, even though it was neither the source nor the target representation of the problem. This observed three- and four-register synergy seems indicative of a simultaneous awareness of other possible registers of representation.
In general, the digital resources appeared to help mediate the participants’ understanding of the situations where a quantity is periodically multiplied by a constant and their associated formulas. As a result there was a general movement toward the underlying concept of an exponential function that could be considered without reverting to an equation or formula. When one of the preservice teachers, Dolly, was asked why her perspective had changed from her preintervention perspective, she indicated that before the intervention, her focus had been on the algebra associated with the constants in y = y0ekx.
The interactive nature of the GoeGebra applets let her see the connections between the different representations of the functions. In short, the digital resources had mediated her recognition of the relationship between situations, tables, graphs and formulas, and correspondingly, her focus had shifted from algebraic procedures to underlying concepts.
Preservice Teachers’ Perspective on Student Understanding. The following are some preintervention responses when the participants were asked what it means to understand exponential functions:
- to be able to solve exponential problems,
- to be able to model situations using exponential functions,
- to know the laws of exponents (for example, an x am = an + m),
- to do both practice problems and exercises and
- to recognize an exponential graph.
Preintervention, all six study participants tended toward circular responses. For example, one of these preservice teachers, Elizabeth, indicated that if students understand exponential functions, then they should be able to solve real world problems. When asked what sorts of real world problems, she indicated “real world problems that use exponential formulas.” Despite subtle hints, she was unable to speak of situations associated with periodic doubling or halving. The basis for deciding whether a situation was “exponential” was if the associated data satisfied y0ekx. Knowledge of exponential functions involved using two data points to obtain the constants and then determining whether the remaining data were consistent with the formula that was obtained. When asked if there was some way to identify an exponential situation without using a formula (such as y = y0ekx or y = y0bx), she indicated that she did not think so.
Preintervention, all six of the preservice teachers in the study seemed to share Elizabeth’s perspective that exponential functions start with a formula. However, evidence suggests this response was more than a privileging of one register over others and, rather, a limitation in the participants’ understanding. The default for all problems involving exponential functions was to go the algebraic register and employ symbolic manipulation. When presented with tables, graphs and situations that involved things doubling, tripling, and so forth, participants appeared to recognize that they were consistent with exponential functions and proceeded to fit them with as y = y0ekx or y = y0bx; however, none of the preservice teacher participants was aware that all exponential growth involves a constant doubling time.
Preintervention, Ismael suggested that students should be able to differentiate exponential functions from other common functions (linear, quadratic, etc.) as a criterion for understanding. However, when this idea was pursued, it became clear that he had trouble describing the conceptual difference between these functions. When he was asked how one should differentiate a linear and an exponential function, he responded that “a linear function is straight and an exponential function curves upwards.” Some prompting was provided to see if Ismael had a quantitative sense of the difference between the two, where the interviewer was looking for periodic multiplication (perhaps expressed with terms such as doubling or halving) versus periodic addition. However, during the interview, Ismael was unable to move beyond superficial geometric differences.
It was not until tables were used as intermediary representations that Ismael was able to make conceptual connections to the unique features of exponential functions. Postintervention, four preservice teachers indicated that they should also be able to differentiate between situations associated with different kinds of functions, including linear, quadratic, and exponential. Five of the six participants spoke of doubling or halving times, and none of the six provided circular responses. When Ismael was asked the difference between linear and exponential functions in the second interview, he drew two tables and without any prompting indicated that with linear you add a constant each time and with exponential you multiply by a constant each time.
The participants not only spoke highly of the digital resources, they seemed to embrace them as a means to understand the synergy of the registers for mathematical concepts as they worked on mathematical problems in the program. They were unanimous in recognizing that these applets provided a visualization that was impossible using traditional tools such as pencil and paper or blackboard and chalk.
Goodhue’s (1995) Task-Technology Fit (TTF) model describes the relationship between the needs of the user and the characteristics of the digital resources being used. His findings showed a direct relationship between the resource’s fit to a task and the use of the resource. If a given digital resource is capable of increasing understanding and helping to extend epistemological boundaries within a particular content area, the TTF model suggests that the technology is also more likely to be adopted.
In short, all of the study participants recognized the importance of the GeoGebra applets in promoting simultaneous awareness of representations and believed that concurrently observing representations would have a powerful impact on their students’ ability to associate representations with the underlying mathematical concept.
Preservice Teachers’ Perspective on Students’ Evaluation. During preintervention and postintervention interviews, all six preservice teachers reported that, while exams are a part of the current educational culture, a significant portion of student assessment should come from projects based on real world situations. Preintervention, the nature of the projects the participants described was to find a situation that could be modeled with exponential functions and to find its associated formula.
Only two preservice teachers offered concrete situations that might be the subject of student projects. Jose suggested a project to find half-life using radioactive dating. Further discussion demonstrated that he was somewhat confused regarding the difference between finding an unknown half-life and using the known half-life of C14 to find the age of an artifact.
Roberto suggested a project to model “the population growth of their school.” When he was asked what students should do if the growth of their school was not exponential, he was unsure and suggested perhaps finding another school that did have exponential growth.
Elizabeth was representative of the remaining teachers. She indicated that students should model exponential situations in their daily lives. When asked what sort of situations, she said, “Situations that are exponential.” When asked how students would know if the situation is exponential, she replied, “If it fits an exponential function.” So the preservice teachers clearly recognized the importance of showing students how mathematics is relevant to the world around them; however, prior to the intervention, their limited understanding of exponential functions impacted how they might effectively demonstrate this relevance in their teaching.
Postintervention, five of the six preservice teachers spoke of finding situations where something doubles or halves at a constant rate and modeling the phenomenon. Four of these said their students should first place data in a table to assure that it, in fact, represented an exponential situation. All five wanted their students to make predictions using their model and then verify whether the predictions were consistent with data.
Jose suggested that students model the area covered by mold on a petri dish. Roberto suggested that students might study the amount of medication or alcohol in a patient’s bloodstream by modeling data that might be obtained from a lab, a hospital, or the internet.
Elizabeth was interested in money in the bank. In particular, she thought exploring the difference between constant and variable interest rates using piecewise functions and translations to graph variable interest rates might be interesting. Her ideas included an exploration between one fixed-rate account investment over 5 years versus five successive 1-year accounts where the interest rate changes each year.
Three of the six preservice teachers suggested that students should discuss what makes a rate of growth (or decay) constant. All of these examples were distinct from the examples given in the program’s online materials that the study participants accessed.
The general belief that students should go out into the world and use mathematics was equally strong before and after the intervention. However, preintervention, the general form for an exponential formula dominated the study participants’ perspectives on what real world situations were consistent with an exponential relation. The GeoGebra applets were credited by five of the six study participants as being fundamental in changing their perspectives. The consensus was that GeoGebra applets allowed participants to see how easily changes in real world situations could be reflected in formulae. Correspondingly, teachers were better able to focus on real world situations and underlying concepts, which changed their perceptions on how best to approach projects associated with exponential functions.
Discussion and Conclusions
Research Question 1 addressed whether and how the intervention could impact the way that preservice teachers make sense of and solve problems that involve conversions between registers. The data in Table 3 show an improvement from the preintervention interview to the postintervention interview in the preservice teachers’ abilities to respond to all questions related to exponential functions. In addition, all the participating preservice teachers changed the way they solved some problems (particularly with conversions to the symbolic register), even when their preintervention strategies were successful. The true impact of the intervention was more likely associated with the way the preservice teachers made sense of the problems.
Our measure of the understanding of a concept was based on achieving a synergy of registers of representations, as determined by the ability to pass between different registers associated with the same concept. The intervention produced two changes in the preservice teachers that were indicative of an improved awareness of the various registers associated with the same mathematical concept. The first was a considerably improved ability to perform unfamiliar conversions between known registers of representation, and the second was a newfound practice of introducing intermediary representations when convenient to do so.
The data in Table 3 show preservice teachers’ abilities to perform conversions between registers of representations of exponential functions. Preintervention, the preservice teachers struggled with less common conversions. For example, when presented with an equation and asked to find any situation that could be associated with this equation, only one participant was able to do so. Postintervention, all preservice teachers were successful on 100% of interview problems with both familiar and unfamiliar conversions, which suggests a pronounced improvement as a result of the intervention.
The second indication that the intervention helped produce simultaneous awareness of registers associated with the same mathematical concept was the participants’ introduction of additional representations as intermediary representations. Preintervention, all of the preservice teachers restricted their vision to the source representation and the target representation. The only time another representation was introduced was for conversions from the verbal register to the geometric register and from the symbolic register to the geometric register, when participants would introduce a table as the transitory auxiliary representation to draw a graph.
Postintervention, the only time that participants did not use a third representation was for conversions from the symbolic register to the numeric register and from the numeric register to the symbolic register. For all other conversions a third representation was voluntarily introduced to lend context to the problem. The voluntary introduction of new representations of the same situation when convenient is consistent with the simultaneous awareness of different registers of representation that is associated with understanding the underlying mathematical concept.
These results indicate that students were, in fact, evolving toward a fluency approach to problems involving conversions between registers. The manner in which this approach changed the way students made sense of problems was evidenced by all conversions to the symbolic register. Preintervention, successful preservice teachers all used the same strategy, an example of which is seen in the preintervention column of Figure 5, and can be summarized as follows:
- Identify that the relationship is exponential.
- Recognize that all exponential relationships can be expressed with either y = y0ekx or y = y0bx. (None of the preservice teachers was able to justify why an exponential relationship can always be expressed with these formulae.)
- Use data points to solve for the unknown parameters.
Postintervention, preservice teachers were successful with all such conversions, and all used the same strategy. This strategy can loosely be described as organizing the numerical data based on a multiplicative factor and the frequency with which this factor is multiplied and then figuring out the associated formula. An example of this approach can be seen in the postintervention column of Figure 5. In contrast to the preintervention strategy, where preservice teachers associated a memorized formula with exponential situations, the postintervention strategy appeared to involve making sense of the formula.
Research Question 2 addressed the extent to which the intervention affected preservice teachers’ perceptions of what it means for a student to understand a mathematical concept. In particular, did the intervention change their abilities to distinguish between understanding a concept and rote memorization of procedures involving the concept? Stylianou (2010) found that
Interviews with middle school mathematics teachers suggest that teachers use representations in varied ways in their own mathematical work and have developed working definitions of the term primarily as a product in problem solving. However, teachers’ conceptions of representation as a process and a mathematical practice appear to be less developed, and, as a result, representations may have a peripheral role in their instruction as well. Further, the data suggested that representation is viewed as a topic of study rather than as a general process. (p. 1)
Such observations were consistent with the participants’ preintervention perspectives. One strong indication that the intervention had impacted the participants’ perspectives on what it meant to understand a concept emerged from the discussion during the orientation session. Before this orientation, the group agreed that a concept should be introduced using a single representation (usually in the algebraic register), and then its associated representations would follow.
With the new perspective, participants accepted the idea that multiple representations are fundamental to understanding a mathematical concept. Preintervention, an equation or formula was often used to define a mathematical concept with corresponding representations in the algebraic register at front and center for the preservice teachers. An emphasis on rote procedures associated with obtaining an equation from other representations resulted, which reduced all problems to symbolic manipulation.
The postintervention perspective was that students show that they understand a given concept when they demonstrate that they understand the commonality of all representations associated with the concept. This perspective seemed to push preservice teachers beyond a focus on procedures associated with finding a formula to the exploration that is needed to understand the commonality of all representations (including real world situations) that are associated with a mathematical concept.
Research Question 3 addressed whether the intervention affected how preservice teachers would evaluate their students. In both the preintervention and postintervention interviews, the preservice teachers were interested in projects to help students use exponential functions in the real world. Preintervention, participants struggled to give form to this vague, generic notion. None of the preservice teachers could describe an exponential situation without a circular reference to the term exponential, while two thirds were unable to verbalize a situation that they deemed appropriate for projects involving exponential functions.
Postintervention, five preservice teachers indicated that students should find phenomena in the real world that either halve or double periodically and use these as the bases for projects. Three of the six felt that their students should either look at phenomena where the doubling or halving rate does not remain constant or contemplate on the physical phenomenon that makes the doubling or halving rate constant. This response is a significant shift from finding a situation that fits with a formula to assessing the causality that makes situations exponential.
The participants’ perceptions of a need for student projects that associate mathematical concepts with the real world did not change. However, the ease with which preservice teachers were able to provide form and context for real world projects and the depth of understanding that these preservice teachers sought from their students showed dramatic increase after the intervention.
The results suggested that the impact of this intervention were quite promising. An orientation was provided and then digital resources were incorporated into preservice teachers’ review for the certification exam. Once the digital resources (i.e., the online GeoGebra applets) were made available, the intervention provided a means for preservice teachers to access the verbal, numerical, geometric and algebraic registers of representation simultaneously. This simultaneous access to all registers of representation, after a brief introduction to a new way of thinking about understanding, seemed to move preservice teachers’ perspectives significantly away from a strictly procedural focus and to a more concept-driven approach to thinking about and doing mathematics.
References
Baxter G., Ahmed S., Sikali E., Waits T., Sloan M., & Salvucci S. (2007). Technical report of the NAEP mathematics assessment in Puerto Rico—Focus on statistical issues. Retrieved from the National Center for Education Statistics website: http://nces.ed.gov/nationsreportcard/pdf/studies/2007462rev.pdf
Duval R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61, 103-131.
The Early Math Collaborative-Erikson Insititute. (2013). Big ideas of early mathematics: What teachers of young children need to know. Boston, MA: Pearson Education.
Goodhue, D. L. (1995). Understanding user evaluations of information systems. Management Science, 41(12), 1827-1844
Hitt, F., Gonzalez, A., & Morasse, C. (2008, July). Visualization and students’ functional representations in the construction of mathematical concepts. An example: The concept of co-variation as a prelude to the concept of function. Paper presented in the 11th International Congress on Mathematics Education, Monterrey, N.L., Mexico. Retrieved from http://tsg.icme11.org/tsg/show/21
Kant, I. (1929). Critique of pure reason. (N. K. Smith, Trans.). London, UK: Macmillan. (Original work published 1781).
McGee D., & Martinez-Planell R. (2014). A study of effective application of semiotic registers in the development of the definite integral of functions of two and three variables, International Journal of Science and Mathematics Education, 12, 883-916.
McGee, D., & Moore-Russo, D. (2015). Impact of explicit presentation of slopes in three dimensions on students’ understanding of derivatives in multivariable calculus. International Journal of Science and Mathematics Education, 13, 357-384.
Moore-Russo, D., & Viglietti, J.M. (2012). Using the K5 connected cognition diagram to analyze teachers’ communication and understanding of regions in three-dimensional space. Journal of Mathematical Behavior, 31, 235– 251.
National Assessment of Educational Progress. (2008). The nation’s report card: Mathematics 2007 performance of public school students in Puerto Rico—Focus on the content areas. Retrieved from the Institute of Education Sciences website: http://nces.ed.gov/nationsreportcard/pubs/studies/2009451.asp
Piaget, J. (1971). Biology and knowledge. (B. Walsh, Trans.). Chicago, IL: University of Chicago Press. (Original work published in French, 1967).
Piaget, J. (1977). Understanding causality. (D. Miles & M. Miles, Trans.). New York, NY: Norton. (Original work published in French, 1971.)
Presmeg, N. (2006). Semiotics and the connections standard: Significance of semiotics for teachers of mathematics. Educational Studies in Mathematics, 61(1–2), 163–182.
Radford, L. (2002). The seen, the spoken, and the written: A semiotic approach to the problem of objectification of mathematical knowledge. For the Learning of Mathematics, 22(2), 14-23
Stylianou, D. A. (2010). Teachers’ conceptions of representation in middle school mathematics. Journal of Mathematics Teacher Education, 13, 325–343
Author Note
Daniel McGee
Kentucky Center for Mathematics
Email: [email protected]
Deborah Moore-Russo
State University of New York – Buffalo
Email: [email protected]
Appendix A
Exponential Growth Interview Questions
![]()