Within this decade, the National Commission on Teaching and America’s Future has estimated that schools will lose 1.5 million baby boomer teachers to retirement (Carroll & Foster, 2010). This significant loss of human capital will exchange the wise experience of veteran mathematics teachers for the youthful enthusiasm of new teachers. At the same time, the nation is raising expectations for thoughtful mathematics instruction, as most states implement the Common Core State Standards (CCSS; National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010).
Across the country, students are having particular difficulty learning algebra. Algebra is the gatekeeper to higher education and future employment in well-paid careers (Moses & Cobb, 2001). Yet, the failure rate is alarming as districts such as Montgomery County, Maryland, report that 82% of their high school students and a total of 5,300 students overall failed the Algebra I final exam (St. George, 2014). In California in 2008, 560,000 students failed Algebra I (Foster, 2009).
In Oregon, 30% of all students (59% of Black and 44% of Hispanic students) failed the state 11th-grade mathematics exam in 2014, which primarily consists of algebra (Oregon Department of Education, 2014). The collision between a growing, inexperienced teaching force and students’ algebra struggles should be one of great concern. If schools are to meet the algebra challenge, preservice teachers’ effectiveness must be accelerated.
Supported by a Fund for the Improvement of Post-Secondary Education grant, the Algebraic Thinking Project (ATP) was a collaboration of four public and private universities in Oregon that restructured mathematics methods courses for secondary preservice teacher candidates. The goal of restructuring was to use the affordances of technology to counteract this loss of experience by increasing preservice teachers’ ability to anticipate and respond to students’ struggles in algebra. Using an integrated technological approach, the research connected with the ATP explored the question, “Can mathematics teacher educators accelerate preservice teachers’ experience with students’ thinking in order to increase their ability to anticipate students’ engagement with algebra?” While our research focused on algebraic thinking, the project is a potential model for other content areas.
Experience With Student Thinking
Over time, veteran mathematics teachers develop extensive knowledge of how students engage with concepts—their misconceptions, their ways of thinking, and when and how they are challenged to understand—and use that knowledge to anticipate students’ struggles with particular lessons and plan accordingly. Veteran teachers learn to evaluate whether an incorrect response is an error or the symptom of a faulty or naïve understanding of a concept. They learn to identify mathematically important pedagogical opportunities (Leatham, Peterson, Stockero, & Van Zoest, 2011) based on the nature of students’ thinking and their curricular goals.
Preservice teachers on the other hand, do not have the same experience they can rely upon that might help them anticipate important moments in their students’ learning. They struggle to make sense of what students say in the classroom and determine whether the response is useful or can advance discussion (Peterson & Leatham, 2009). They may assume students’ understanding and fail to perceive when a student’s thinking is problematic. The art of orchestrating productive mathematics discussions, for instance, depends on “anticipating likely responses to mathematical tasks” (Smith & Stein, 2011). However, lacking experience in the classroom, preservice teachers struggle to anticipate students’ thinking.
Learning to foresee and use students’ thinking during instruction is complex, especially for preservice teachers (Sherin, 2002). The Cognitively Guided Instruction project (CGI) found that teachers who learned how elementary students think could predict their struggles. They made fundamental changes in their beliefs and practice that ultimately resulted in higher student achievement (Carpenter, Fennema, Loef-Franke, Levi, & Empson, 2000).
Ball, Thames, and Phelps (2008) defined this domain of Mathematical Knowledge for Teaching as Knowledge of Content and Students (KSC).“KSC includes knowledge about common student conceptions and misconceptions, about what mathematics students find interesting or challenging, and about what students are likely to do with specific mathematics tasks” (Ball, Bass, Sleep, & Thames, 2005, p. 3). CGI researchers found that teachers with higher amounts of KSC facilitated increased student achievement, and these effects were longlasting for students and teachers (Fennema, et al., 1996). KSC is traditionally acquired by experience in the classroom—exactly what preservice teachers lack.
For decades, researchers have worked to define students’ struggles, misconceptions, and ways of thinking about algebra. Over 800 articles have been written that research, analyze, and discuss how students engage with algebra. This vast knowledge base has been essentially inaccessible to teachers because of its sheer size and the research format that often requires significant time from which to glean usable information—time that teachers do not have. To address preservice teachers’ lack of experience with student thinking and the resulting limits in their ability to anticipate the ways their students’ interpret and interact with mathematics, the ATP staff read 859 articles and synthesized the research into multiple technology-based resources.
The project resources served two populations. First, the resources provided the project’s mathematics teacher educators with a variety of tools they could use for instruction. Through an integrated approach our project aimed to help preservice teachers develop the disposition and knowledge to anticipate students’ struggles and ways of thinking as they prepared their lessons, made instructional decisions, facilitated student learning, and debriefed their instruction. Veteran teachers do this based on experience, but preservice teachers lack this experience, and the ATP resources are intended to bridge this gap.
Second, the ATP resources that are integrated in teacher education programs can become essential, easily accessible, and usable resources for those first 5 years of teaching, in which early career teachers need support in anticipating and interpreting students’ thinking in algebra. Early career teachers’ anxiety over assessment and student results contributes to their attrition because they lack confidence in monitoring and reporting on student progress (Ewing & Manuel, 2005).
The first 3 to 5 years of a teacher’s career involve significant improvements in their practice, which then tend to level off (Hanushek, Kain, O’Brien, & Rivkin, 2005). These years are critical for the students they teach. The dire algebra statistics suggest teacher educators need to accelerate the process whereby teachers develop the professional expertise they need to be effective.
ATP’s Technology-Based Resources
A team of 17 mathematics educators and middle and high school teachers read 859 articles on students’ algebraic thinking and identified what might be useful for preservice teachers. The synthesis of research resulted in an integrated approach to preparing mathematics teachers using four technology-based resources housed at the Center for Algebraic Thinking website (Resources are freely accessible at http://www.algebraicthinking.org):
- Encyclopedia of Algebraic Thinking,
- Student Thinking Video Database,
- Formative Assessment Database and Class Response System, and
- Virtual Manipulatives.
The Encyclopedia of Algebraic Thinking consists of 66 entries that articulate students’ misconceptions and ways of thinking about algebra. The research on students’ algebraic thinking typically includes a discussion of the mathematics involved in a misconception or way of thinking, assessment problems, statistics on students’ responses to problems, transcripts of interviews with students describing their thinking, and suggested instructional strategies. Construction of entries in the Encyclopedia of Algebraic Thinking were guided by five questions:
- What CCSS does this research address?
- What is the symbolic representation of thinking with the idea? (What does it look like? How does students’ written work indicate how they are thinking about the idea?)
- How do students think about the algebraic idea? (What does it sound like? What do students say when they discuss the idea?)
- What are the underlying mathematical issues involved? (What prerequisite knowledge is involved, what concepts are essential, and where does the concept fit in mathematics?)
- What research-based strategies/tools could a teacher use to help students understand?
The Encyclopedia is searchable by CCSS, keyword, and cognitive domain for teachers in non-CCSS states. Based on the research, typical algebra textbooks, and the CCSS, the project defined five cognitive domains around which ATP staff organized the articles reviewed: Variables & Expressions, Algebraic Relations, Analysis of Change, Patterns & Functions, and Modeling & Word Problems. Our mathematics teacher educators used the Encyclopedia for four purposes.
- Make preservice teachers aware of the range of ways students may think about algebra and the nature of misconceptions they can develop.
- Help preservice teachers acquire a disposition towards wanting to learn about students’ thinking through exploration of the entries.
- Provide preservice teachers with a just-in-time resource to help them anticipate how students might interact with an algebraic concept in their lesson, in an effort to compensate for their relative lack of experience with students’ thinking.
- Reflect on and interpret their experience of interacting with students’ thinking during a lesson to facilitate their next instructional decisions.
In order to help mathemathics teacher educators engage preservice teachers in considering students’ thinking, 20 different problems were identified in the research that were representative of typical concepts that students struggle with across the five cognitive domains identified by the project. Two different sets of 10 problems were created from the original 20. The two different forms were alternated as they were given to 17 middle school students to get a breadth of response to the 20 problems. Each student worked on the problems for between 10-30 minutes. Each student was then asked by ATP staff to explain their thinking with each problem as they were videotaped. The result was approximately 170 video clips, one for each problem for each student. Of those video clips, 68 had useful explanations (other than “I don’t know”, etc.) and were combined into a Video Database. The Video Database is freely available at the project website (http://www.algebraicthinking.org/) when users establish a free account.
Video has proven to be a useful tool for teachers to consider students’ thinking (Franke, Carpenter, Fennema, Ansell, & Behrend, 1998; Gearhart & Saxe, 2004) and can provide a more dynamic environment in which to consider students’ thinking than can text. The video clips were used as a significant part of 15 project-designed instructional modules for mathematics methods courses from which our math educators could choose to implement. The intent of the video is to allow preservice teachers to hear why students struggle or make choices as they engage in a problem.
The National Education Technology Plan (2010) recommended that educators “diagnose strengths and weaknesses in the course of learning when there is still time to improve student performance” (p. 9). However, one of the stressors for preservice teachers is their lack of confidence in monitoring the status of their students’ understanding of the mathematics. One key feature of the research literature is assessment problems designed to elicit students’ range of algebraic thinking. The ATP catalogued these empirically tested problems into a Formative Assessment Database for preservice teachers to assess their students’ algebraic thinking.
The web database is searchable by keyword, CCSS, and cognitive domain. Problems range from “Which is larger, 2n or n + 2?” (Kuchemann, 2005) to more complex problems, such as the Smith Family Holiday Problem shown in Figure 1.
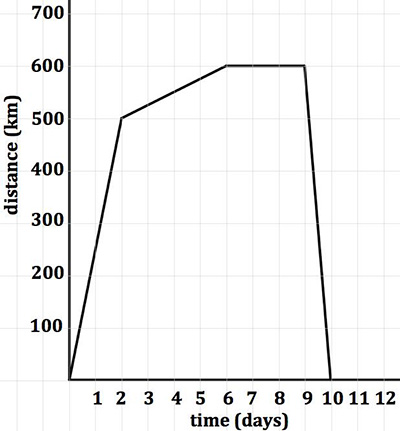
The Smith family’s whole holiday is shown on the graph at left. The vertical axis shows the distance in kilometers away from home. The horizontal axis shows the time in days since the start of their trip.
a) During which days did the Smith family travel fastest?
b) They stayed with friends for a few days. Which days were these?
c) On average, how fast did the Smith family travel to get to their destination?
Figure 1. Smith family holiday problem. Graph recreated based on problem published in “An ‘Emergent Model’ for Rate of Change” by S. Herbert & R.. Pierce, 2008, International Journal of Computers for Mathematical Learning, 13, p. 240. Copyright 2008 Springer Science+Business Media B.V.
Although the first problem may appear simplistic, it addresses complex understanding of the concept of a variable as an unknown. The student must articulate how variation in one set of values depends on variation in another set and the relative power of operations on a range of numbers. The Database provides teachers with information about how students in the study responded. For instance, with the first problem, 71% of 11 to 13-year-old students believed that 2n would be greater, 16% believed n + 2 would be greater or that they would be the same, while only 6% responded correctly that the answer is 2n when n > 2 (Hart et al., 1981).
The second problem examines students’ understanding of rate of change. Researchers found that common incorrect answers included that days 1 and 2 the family traveled the fastest because they are the steepest. Many students saw a steep upslope but did not see a steep downslope. Other students responded that the fastest days would be 3, 4, 5, and 6 because they are the flattest. A formative assessment problem such as this one creates the opportunity for teachers to learn the status of multiple aspects of their students’ understanding of a concept.
While the problems are usable in paper and pencil format, the ATP staff also developed a Classroom Response System (CRS) that directly accesses the Formative Assessment Database. The literature on CRS has shown that technology enhanced formative assessment can increase student participation and reshape teacher discourse patterns (Feldman & Capobianco, 2008; Langman & Fies, 2010).
The unique aspect of our CRS is that it allows teachers to use problems from the database or write their own and deliver them to students in the classroom on mobile devices. Students answered the problem(s), then the app collected the data and instantly provided teachers with easy-to-consume, graphical evidence of the range of students’ thinking. The preservice teachers could immediately see how the class understood a concept on a single problem or could look at an individual student’s understanding across all problems.
Finally, the ATP developed 17 iOS-based virtual manipulatives that address specific algebraic concepts identified in the research as challenging for students to understand. The National Council of Teachers of Mathematics (2000) suggested that virtual manipulatives can allow students to “extend physical experience and to develop an initial understanding of sophisticated ideas” (p. 27). They can be powerful tools for learning, providing significant gains in achievement (Heid & Blume, 2008; Suh & Moyer-Peckenham, 2007). However, “one reason that educational software has not realized its full potential to facilitate and encourage students’ mathematical thinking and learning is that it has not been adequately linked with research” (Sarama & Clements, 2008, p. 113).
Accordingly, the ATP used research on algebraic thinking as the basis for manipulative development. Our apps typically have students manipulate and explore a dynamic between variables. For example, one app addresses research by Monk (1992) that students tend to draw graphs that imitate reality, such as a hill, regardless of the labels of the axes. Our Action Grapher app (see Figure 2) shows a biker climbing various hills while simultaneously three separate graphs of height, distance, and speed versus time appear alongside. Student draw what they think each graph will look like, then animate the bike and compare their hypotheses against the graphs that unfold.
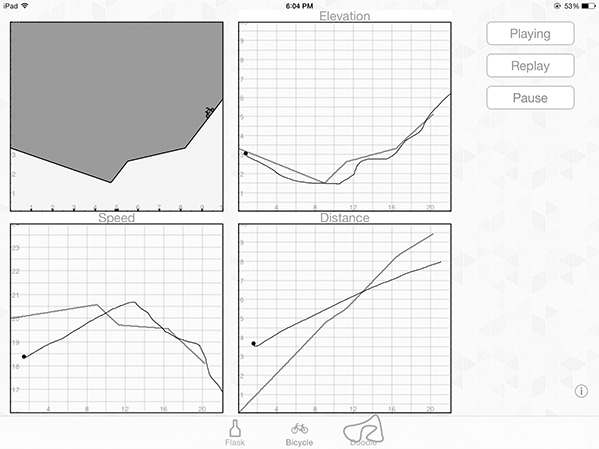 Figure 2. Action grapher.
Figure 2. Action grapher.
“Technologies often afford newer and more varied representations and greater flexibility in navigating across these representations” (Mishra & Koehler, 2006, p. 1028). The Action Grapher app provides that opportunity for students to observe changes across representations and creates cognitive conflict for those students who have the misconception described by Monk (1992). The ATP virtual manipulatives take little time and focus on a specific, challenging concept or misconception. The purpose of these apps was to nurture preservice teachers’ orientation toward their students’ algebraic thinking. Since these apps target hard-to-understand topics in algebra, preservice teachers needed to consider the following:
- The nature of the challenge to students’ thinking the virtual manipulative addressed.
- How the app addressed a misconception or way of thinking about the concept.
- Why that might be an effective approach.
Together, the four technology-based resources were designed to be an integrated strategy to develop preservice teachers’ focus on students’ thinking, understanding of the nature of students’ thinking, ability to assess the range of their students’ thinking, and ability to intervene in a research-based way upon that thinking. It is unrealistic to believe that preservice teachers could acquire all the knowledge they need regarding students’ thinking in a teacher preparation program. Accordingly, the intent of the project was not simply to fill preservice teachers’ brains with research but to orient them toward their students’ thinking and develop a habit of mind to use technology-based resources to prepare for and interpret students’ engagement with algebra.
No known research exists regarding a similar comprehensive approach toward infusing technology into teacher preparation in mathematics. While our use of a web-based encyclopedia, video database, formative assessment database, and iOS apps in combination is unique in teacher preparation, each element has a research basis, as indicated in each of the previous sections on our tools.
Much discussion has occurred around the concept of technological pedagogical content knowledge (Voogt, Fisser, Pareja Roblin, Tondeur, & van Braak, 2013). The technology, pedagogy, and content knowledge (TPACK) framework captures the complex dynamic between teachers, their content, and resources—focusing on the knowledge needed for implementation of technology in the classroom (Mishra & Koehler, 2006). The pedgogical knowledge element of TPACK includes knowledge about how students learn and methods of assessment that is the heart of our work (Harris, Mishra, & Koehler, 2009).
Heid and Blume (2008) noted that there is a “considerable amount of research focused on the effects of technology on the development of the concept of function and on the role of technology in enhancing symbolic manipulation skills and understanding” (p. 58). Significant research also has examined how teachers use technology, particularly graphing calculators (Zbiek & Hollebrands, 2008). Although research indicates that technology is changing the way individuals think about and do algebra, research is not yet clear on technology’s role in developing capable preservice teachers. This project is an effort to use technology in many forms to prepare teachers for success in the algebra classroom.
The Research Study
Participants
The research study was implemented by four public and private universities in Oregon with mathematics teacher preparation programs. Each institution was charged with restructuring their mathematics methods courses to implement the technological resources of the ATP. In the third year of the 4-year study (the year for which results will be conveyed in the paper), the courses included 45 preservice teachers (25 female) working toward teaching licenses in basic or advanced mathematics. The public institution had 28 students, with the rest spread equally across the other institutions. Approximately 30% of participants entered the teacher education programs with mathematics degrees.
The mathematics methods programs at three institutions were entirely graduate, Master of Arts in Teaching (MAT) degree programs. At one institution, undergraduate students also participated in the mathematics methods courses, so that 25% of participants overall did not yet have a Bachelor of Arts degree. Field experience and mathematics methods course requirements were the same for both Bachelor of Arts and MAT programs. Case study participants were chosen based on their being placed in an Algebra I class for their student teaching experience and willingness to participate in the study.
Design of the Study
Multiple differences existed across the four ATP institutions in regard to coursework and timing. However, we were all under the same state regulations for teacher education, so the content of our coursework and field experiences were very similar. Whether undergraduate or MAT student, each teacher candidate experienced the same coursework within an institution. For undergraduates, the coursework was distributed over 2 years, with the field experiences distributed across the final year.
Each of the MAT programs had part-time as well as full-time options. One institution was on the quarter system, and the other three were on the semester system. The mathematics methods courses are offered at different points in the programs across the final year that includes field experiences. At two institutions the methods course occurred in the fall, while at the other two the methods course was distributed across two semesters. Participants in the study were all preservice teachers enrolled in our mathematics methods courses seeking either a Middle Level or High School Level teaching license or both.
Each institution was free to choose which elements of each resource were most useful in their mathematics methods programs. All methods instructors used at least one module, used video clips of students explaining their thinking during class, referred preservice teachers to the Encyclopedia for information about students’ thinking or required citations from the Encyclopedia in assignments, oriented preservice teachers to the formative assessment database, and discussed ATP apps.
To determine the effectiveness of the resources and approach to developing preservice teachers’ knowledge of students and content as well as their habits of mind in using the resources, the study included quantitative and qualitative data. For quantitative data the project designed a preservice teacher survey. For qualitative data the project conducted eight case studies, including video of preservice teachers’ instruction that was coded with the project-designed Teacher Dispositions Towards Students’ Thinking (TDST) observation tool.
Preservice Teacher Disposition Survey. The ATP staff constructed and pilot tested the Teacher Disposition Survey, containing 24 items that solicited self-reported perceptions about the degree to which preservice teachers valued and used student preconceptions in their teaching. The survey was based on a survey used by Nathan and Koedinger (2000) and Nathan and Petrosino (2003) that assesses six areas pertaining to the utility of symbol-based (rather than word-based) mathematical forms, student preconceptions and intuitive means for solving problems, and ways teachers work with student preconceptions and intuitive problem-solving methods in class. Items were pulled from this survey and combined with original items about whether or not teachers think students have preconceptions about math, qualities of those misconceptions, and how teachers work with student preconceptions to teach effectively.
Data collected with the ATP survey was annually assessed for item reliability. In 2012, 17 preservice teachers completed the survey, which included 24 original items used to assess their beliefs about the role of students’ thinking in effective mathematics instruction. These 24 items were developed with the project team to support content validity targeted at the objectives of the program. Cronbach’s reliability for the items was high at 0.83, with only three items indicating item-rest correlations above 0.3. In 2013, the survey’s reliability went up to 0.88 (n = 19), with only one item indicating an item-rest correlation of greater than 0.3. Each preservice teacher was given a pretest survey at the beginning of the mathematics methods program and a posttest at the end of the school year. The survey data were used in combination with observations and interviews to describe teacher dispositions and classroom strategies.
Case Studies. In order to learn about the nature of preservice teachers’ orientation toward using their students’ thinking to inform their instruction and understand how preservice teachers used project resources, each of the four institutional Core Team members was responsible for two case studies of their students. The case studies started with an interview at the beginning of the teacher education program. The interviewer presented an algebra problem to the candidates, then asked them to solve it and then discuss how they believed a student might approach the problem correctly or incorrectly. Then the interviewer and candidate viewed a video of a student discussing his thinking with the problem. Candidates explained how they might work with that student.
Next, the interviewer asked how the candidate might approach teaching an algebra topic. This process was repeated in a postinterview at the end of the mathematics methods course of the institution. In addition, the case studies included work samples (teaching units) from each candidate and reflections in which the candidates discussed their teaching and how they made use of students’ algebraic thinking and the resources of the project.
A key part of the project involved observing preservice teachers in inquiry sequences, or interchanges, where they helped students explore and better understand a topic. Video of the case study preservice teachers’ instruction was taken at the beginning, middle, and end of their field experience to assess changes in their instructional practice. Our four institutions’ field experiences varied from 10 weeks to a full semester (18 weeks). The project used videos to analyze preservice teachers’ interactions with students using the ATP’s TDST. The TDST was developed and field tested by outside evaluators on the staff of the International Society of Technology Educators during the first year of the project. The evaluators trained project team members in how to use the tool to analyze video. In order to increase reliability of the coding, two evaluators each coded a video separately and then conferred to resolve differences and came to consensus on accurate final codes.
The TDST is a custom-built, classroom observation instrument based upon research and methodologies used to describe classroom discourse (Thadani, Stevens, & Tao, 2009; Wells & Arauz, 2006) and student inquiry in the classroom (Fennema et al., 1996; Franke, Carpenter, Levi, & Fennema, 2000; Puntambekar, Stylianou, & Goldstein, 2007). It allowed observers to record qualities of teacher-student interactions, including question-oriented inquiry sequences, teacher lectures, student work, and other instructional activities.
Content validity for the TDST was based on an extensive review of the literature on classroom discourse. Evaluators worked with the project team to refine observational indicators for each area assessed, conducted field testing of the instrument and observer calibration/rater reliability (both project evaluators conducted observations, discussed their coding, and refined the instrument), and conducted two trainings with the project team. The technology of the tool is built upon an existing tool—the ISTE Classroom Observation Tool—that has been used in hundreds of classrooms since 2008.
In addition to data about setting, context, and initiation, an observer using the TDST noted frequencies of interactional qualities that characterized an interaction, including the following:
- Frequency and length of inquiry sequences;
- Characteristics of the setting, including class size, student demographics, subject;
- Initiation of each sequence, including initiator (student or teacher) and technique (question, directive), student groupings (whole class, small group, individual); and
- Types of teacher and student interactions for each sequence:
- Confirm: Teacher or students respond typically with “yes” or “no” to a question.
- Logistics: How class activities and workload are ordered.
- Status check: The degree to which student(s) understood the material.
- Recall/replicate: Access, name, or recall a piece of information.
- Basic operational: Use an algebraic concept, solve a problem or execute a procedure.
- Advanced operational: Use an algebraic tool in an original context, going beyond basic drill and practice. Use a math concept in a complex scenario such as a word problem.
- Conceptual: Abstract qualities of and relationships among algebraic concepts, how/why the concept functions external to a concrete situation; analysis of underlying principles.
- Metacognition: Students reflect upon what they learned and how they learned it.
For instance, a student may ask the teacher, “Am I doing this right?” The teacher may check the student’s work, and use the opportunity to successfully segue into a discussion about the relevant concept underlying the problem solving exercise. This sequence would be recorded as Individual (context); Student, question (initiation); Student “Status check”; Teacher “Basic operational”; Teacher “Conceptual”; Student “Conceptual.”
With the TDST, observers constructed an empirical record describing frequencies of interactions and their qualities, permitting analysis of sequential observation data (as in Bakeman, 2000; Bakeman & Gottman, 1997). ATP staff triangulated observational data from the TDST with survey and interview data to describe changes in teachers’ orientations toward student thinking over time. We hypothesized that ATP teachers learned to anticipate students’ thinking and, as a result, were more interested in how students thought about a topic, rather than if students could simply solve a problem, and engaged students in more conceptual discussion as the year progressed.
Results
The ATP was in its fourth and final year of the grant at the time of this writing, so results conveyed in this paper are based upon data collected in the third year (first year of implementation). In this section are results from the Teacher Disposition Survey and one of the case studies. The quantitative data gathered from the Teacher Disposition Survey gave the researchers a midproject glimpse into the overall impact of the technology-based resources. After the completion of the project, a larger sample size will be available for additional quantitative analysis.
At this point in our data collection we can examine the impact of the technology-based resources on an individual preservice teacher’s practice through one of our case participants, Jessica. This case provides an illustration of how the project resources may be used by teacher educators in other settings.
In regard to the Teacher Disposition Survey, 19 of the 45 participants took both the pre- and posttest. The low response rate was due to multiple variations in students’ participation in mathematics methods courses, as only 19 took the entire mathematics methods program at the four institutions for the full school year. Noticeable gains in awareness and use of ATP resources suggest that mathematics methods instructors had some success integrating them into their courses (see Table 1). ATP applications for use on mobile devices were most popular with preservice teachers. Teacher candidates also reported moderate use of the Encyclopedia.
Pre-post comparisons suffer from inconsistent timing of administration, as teacher candidates took their surveys at different times and mathematics methods programs were of different durations across schools, so time lapsed between pre and post varied by institution and individual.
Table 1
Teacher Disposition Survey Results
Pre (19) | Post (19) | |||
Level of Use | n | % | n | % |
| Encyclopedia of Algebraic Thinking | ||||
| I don’t know what this is | 15 | 79% | 4 | 21% |
| I know what this is, but never used it | 3 | 16% | 4 | 21% |
| I used this 1 or 2 times | 1 | 5% | 7 | 37% |
| I used this a few times | 0 | 0% | 2 | 11% |
| I used this monthly | 0 | 0% | 2 | 11% |
| I used this weekly | 0 | 0% | 0 | 0% |
| iPad/iPod applications from ATP | ||||
| I don’t know what this is | 6 | 32% | 0 | 0% |
| I know what this is, but never used it | 8 | 42% | 1 | 5% |
| I used this 1 or 2 times | 3 | 16% | 4 | 21% |
| I used this a few times | 1 | 5% | 5 | 26% |
| I used this monthly | 1 | 5% | 5 | 26% |
| I used this weekly | 0 | 0% | 4 | 21% |
| Formative Assessments from ATP | ||||
| I don’t know what this is | 18 | 95% | 9 | 47% |
| I know what this is, but never used it | 1 | 13% | 6 | 32% |
| I used this 1 or 2 times | 0 | 0% | 2 | 11% |
| I used this a few times | 0 | 0% | 1 | 5% |
| I used this monthly | 0 | 0% | 1 | 5% |
| I used this weekly | 0 | 0% | 0 | 0% |
Twenty-four items assessed preservice teachers’ beliefs about the role of students’ thinking for instruction. This portion of the survey demonstrated good reliability with a Cronbach’s alpha level of 0.88, with only one item exhibiting an item-rest correlation of less than 0.3 (“Eliciting misconceptions from students only reinforces bad math habits”). As with the items around use of ATP resources, beliefs held by preservice teachers were supportive of the ATP project, specifically, around the idea that student preconceptions about mathematics are important (see Table 2).
All negatively worded items (indicated) were recoded inversely on scales of 1-4 from Never true to Always true and including I don’t know. Comparing all responses from both the 2011-12 and 2012-13 cohorts, the latter exhibited more positive views about understanding students’ thinking—average (group) responses to every item were more positive. However, when considering the respondents who completed both pre- and postsurveys, there was generally no change in attitude over time, save a significant decline for two items (p < 0.05): “Eliciting misconceptions from students only reinforces bad math habits,” and “In my teaching, I feel compelled to find out what my students are thinking.”
Table 2
Pre-Post Teacher Disposition Survey Change
Prompt | Change |
| For any math topic, students have preconceptions that they will apply to what they are learning. | -0.42 |
| Students come to any new math class with misconceptions about how math works. | -0.26 |
| Students enter the algebra classroom with intuitive methods for solving algebra story problems | -0.05 |
| Student misconceptions about math are oftentimes deeply held | -0.05 |
| Student misconceptions about math are usually complex | -0.11 |
| In my teaching, I feel compelled to find out what my students are thinking | -0.37* |
| Identifying student misconceptions is an important part of effective instruction | -0.05 |
| Teaching students the correct math is more important than examining their preconceptions (inverse) | -0.21 |
| Understanding student preconceptions about math is more important than direct instruction on how to solve problems | 0.00 |
| As a teacher, it is worth my time to explore students’ preconceptions in class | -0.16 |
| Eliciting misconceptions from students only reinforces bad math habits (inverse) | -0.74* |
| Working with misconceptions helps students learn math more than direct instruction for correct methods | -0.37 |
| Understanding what is going on in students’ minds is necessary to effectively help them learn algebraic thinking | 0.16 |
| Learning about how students think when doing a problem is worth my time as a teacher | -0.11 |
| Directly teaching a student how to solve a problem is a better use of time than learning why they are making mistakes (inverse) | 0.11 |
| Good teaching requires teachers to use student preconceptions to make instructional decisions | -0.05 |
| If I understand a student’s thinking about a problem, I can improve his/her understanding of math | -0.05 |
| It is not necessary for me to understand a student’s way of thinking – I just need to do a problem correctly (inverse) | 0.11 |
| Teachers should encourage students’ own solution approaches to algebra problems even if the solutions are inefficient | -0.21 |
| The goals of instruction in mathematics are best achieved when students find their own methods for solving problems | -0.05 |
| Students best acquire mathematical knowledge when taught specific methods for solving problems (inverse) | -0.05 |
| Rewarding right answers and correcting wrong answers is an important part of teaching | -0.32 |
| Students need explicit instruction in order to tackle complex algebra story problems (inverse) | -0.05 |
| Teachers should demonstrate the right way to do a problem before the students try to work it out (inverse) | -0.16 |
| *Significant to p < 0.05 | |
A Case Study of Jessica
Jessica’s case was chosen for this article because her demographics were representative of the majority of participants in the study, and her participation in mathematics methods courses was consistent. She was an undergraduate, initial licensure candidate in mathematics. Her preparation included significant coursework in math followed by a 1-year intensive teacher education program at a regional public university. She completed three field experiences in math classrooms: a 16-week practicum, 11 weeks of part-time student teaching at a middle school, and 11 weeks of full-time student teaching at a high school. As a part of the final year, Jessica took two 11-week terms of Content Pedagogy: Mathematics (also known as mathematics methods courses).
The instructor of the course utilized the Encyclopedia of Algebraic Thinking, the project’s instructional modules with the video database, and iPad apps as new additions to the course curriculum. The instructor introduced the Encyclopedia of Algebraic Thinking during a lecture in the first course, and students used the Encyclopedia in class during an Informal Procedures and Student Intuition module. The students also used the Encyclopedia when they researched student misconceptions about algebra for an assignment in which they critiqued an app that claimed to address a misconception. In the first course, students accessed project resources, the course website, and mathematics apps. In the second term of the course, the preservice teachers participated in an embedded field experience where they worked with low performing high school algebra students.
Each week the high school teacher emailed teacher candidates the course objectives and identified appropriate iPad apps for preservice teachers to use with small groups of students. A variety of data were collected to inform the researcher about the case study participant including pre- and postterm administrations of the Teacher Disposition Survey. Jessica was interviewed before and after the mathematics methods sequence, and during full-time student teaching Jessica videotaped three teaching episodes. She wrote reflections on those lessons and reflections on three others.
Content Knowledge. The data indicate that Jessica’s mathematical content knowledge had gaps. During her third teaching episode, a student answered a question with y = 2x + (-4). A fellow student challenged him and claimed that the correct answer was y = 2x – 4. During the ensuing discussion, Jessica acknowledged that + (-4) and -4 were equivalent, but she warned that if students wrote + (-4) on the test, then they would be marked wrong. It is concerning that she established grading procedures that did not align with what is true mathematically.
In her second interview, Jessica demonstrated more areas of concern. She was asked, “How do students understand the difference between expressions and equations?” She did not know what expressions and equations were and asked for an example. The interviewer said, “An expression would be like 3x + 2 and an equation would be like 3x + 2 = 7.” She was then able to answer the question, but did so with uncertainty.
She was then asked, “Let’s say you are going to teach students to understand functions, how might you go about teaching it?” Her answers focused mainly on the idea that functions passed the vertical line test. She mentioned three times that functions were always continuous and that the vertical line test proved this. This was a misconception regarding functions. She was also asked, “How do you think your students might understand nonlinear functions versus linear functions?” Her response focused on the horizontal line test, which is not a test that can distinguish between linear and nonlinear functions.
Pedagogical Knowledge. The data suggest that Jessica had an understanding of sound pedagogy and believed that conceptual understanding by students was critical. However, the teaching videos did not provide evidence that she was able to teach with these in mind. In her initial interview she watched a video clip of a student who had misconceptions about a math task. She was asked, “What would you do with this student to help him understand? What don’t you know about that students’ thinking that you would want to know? How would you answer those questions?” She was able to list a wide variety of techniques for eliciting student thinking, including conceptually focused questions, formative assessment strategies, and additional tasks.
Although the data indicate that she knew how to teach for conceptual understanding, her teaching videos did not show any examples of questions at that level. Three 50-minute clips were coded with the TDST. In total, Jessica asked nine Status Check questions, 37 Recall/Define questions, and 67 Basic Operations questions. She asked only one Conceptual Question (“Why?”). In this instance, the student responded, “I don’t know,” and Jessica proceeded to explain the process to him.
The data indicate that Jessica was aware of the disconnection between her pedagogical beliefs and knowledge and her practice. In the second Content Pedagogy: Mathematics course, Jessica audio recorded herself working with a small group of algebra students. She took a 10-minute clip and analyzed all of the questions that she asked. In her reflection, she stated,
I noticed that I was asking questions to get an answer, but the intention behind those answers was to do a status check and see if the student knew the processes of the different techniques. I also found that even when I was trying to relate what the student was working on to what he had recently learned, my questions came out as [Status Check] questions. I was surprised that even though I know my intention is to verify student understanding and get them to explain their reasoning, that my questions didn’t really reflect that.
Jessica had a goal of getting students to explain their reasoning but struggled to act on it.
Formative Assessment. Evidence indicated that Jessica implemented formative assessment practices in her instruction but did not use this assessment to inform her instruction. In her Teaching Videos 2 and 3, Jessica asked the class what the correct answer to a problem was. The choral response indicated that there were a variety of answers that students believed. Jessica agreed with students who were correct and did not address incorrect responses. At one point, she invited a student to come to the board to share how he did a problem. When he said he did not know how to do it, she instructed him on what to put down for the solution to the problem. Finally, there were three instances where students in the class demonstrated that they were not able to distinguish between positive and negative slopes of lines.
In each case she corrected the student, but did not do any intervention to address the problem. When reflecting on these teaching episodes, Jessica indicated that students did understand the objectives that she set, citing students’ assignments, quizzes, and small group discussions as evidence of understanding. She did not indicate concerns regarding these incidents.
Summary
Based on the analysis of the case study data, there were some successful aspects of the ATP demonstrated in the data. In the interviews, Jessica mentioned that she used what she learned from the Student Intuition Module activity in the class. She explained that the Cover Up technique she learned from discussion about research on students’ mathematical intuition and one of the project’s iPad apps was a strategy she taught and that she felt it really addressed the needs of the students. This assertion was supported by the video data where she used ATP-designed virtual manipulatives in two of the three lessons documented.
However, the data also indicated areas for further improvement of the courses. The lessons that Jessica taught using virtual manipulatives did not demonstrate strong skills for teaching with technology. The lesson objectives were somewhat procedural, and there was less emphasis on conceptual thinking. The methods course did not emphasize the use of the Encyclopedia of Algebraic Thinking in lesson planning, and the Formative Assessment Database was not used in course activities. Both of these tools have the potential to help preservice teachers focus on conceptual understanding in lesson planning. The instructor indicated plans to incorporate those tools into instruction for subsequent methods courses.
Discussion
The ATP used an integrated approach, in which multiple technology-based resources were made available to mathematics methods instructors that were intended to increase teacher candidates’ orientation toward and anticipation of students’ thinking in their classrooms. Mathematics teacher educators each used the resources differently, as they felt appropriate for the timing of content in preservice teachers’ student teaching, as well as other factors related to their courses.
Although we chose some common tools, no assignments or way of using those tools were common across courses. This flexibility was considered a strength of the project but complicated the data analysis and interpretation of results in responding to the research question. As a result, although the case study indicated impact of some resources on one preservice teacher, we cannot point to a particular resource that had a specific impact on all our teacher candidates. The project resources must be evaluated as a whole.
The results of our primary quantitative tool to measure changes in teacher candidates’ dispositions indicated no significant change in their orientation toward students’ thinking except for two items: “Eliciting misconceptions from students only reinforces bad math habits.” This item is important, as the decrease in response suggests that preservice teachers became more aware of the value of eliciting and directly addressing students’ misconceptions in class rather than assuming that correct instruction will overcome bad math habits. Unexpectedly, the other item of significant change, “In my teaching, I feel compelled to find out what my students are thinking,” indicates an opposite conclusion. Further exploration of both of these items through interviews may lead to greater clarity on the project’s impact.
Dispositions can be as important in teacher quality as pedagogical or content knowledge (Singh & Stoloff, 2008). However, “Despite all the emphasis on dispositions, professionals believe that dispositions are a vague construct that is hard to define and measure” (Singh & Stoloff, 2008, p. 1170). Researchers distinguish between character-related and competence-related dispositions (Jung & Rhodes, 2008). The latter was our focus, as the project expected our preservice teachers to increase their interest in exploring and understanding students’ algebraic thinking and their practice of anticipating that thinking as they planned lessons. The data indicated that preservice teachers appear to be entering teacher education programs with attitudes that student thinking is important. However, how they define student thinking and the role that it might play in their teaching may change without influencing their choices on our assessment of their dispositions.
While the Teacher Disposition Survey did not provide quantitative evidence of broad change in our qualitative research, particularly in teacher candidate reflections and interviews, the resources appeared to be having an impact on their orientation toward student thinking and their efforts to anticipate students’ experience of the mathematics. Without quantitative evidence to support that assertion, we cannot conclude with confidence that project resources had the intended impact. Our future task will be to find or design an instrument that is more adept at assessing the subtle changes in preservice teachers’ orientation, as well as implementation of their disposition toward students’ thinking.
Furthermore, preservice teachers are often initially overwhelmed at the complexities of teaching. Borich (2000) described a hierarchy of concerns that developing teachers experience: (a) a focus on their own well-being; (b) a focus on the content they are teaching; and (c) a focus on the impact of instruction on learners. Preservice teachers’ ability to focus on the experience of their students may take some time to develop. The window for impact of our resources may, therefore, extend into their first few years of teaching. A longitudinal study may have potential for determining in the long run whether the combined technological resources of the ATP have the intended impact of helping to make up for their lack of experience with students’ thinking.
References
Bakeman, R. (2000). Behavioral observation and coding. In H. T. Reis & C. M. Judd (Eds.), Handbook of research methods in social and personality psychology (pp. 138-159). New York, NY: Cambridge University Press.
Bakeman, R., & Gottman, J. M. (1997). Observing interaction: An introduction to sequential analysis (2nd edition). Cambridge, UK: Cambridge University Press.
Ball, D. L., Bass, H., Sleep, L., & Thames, M. (2005, May). A theory of mathematical knowledge for teaching. Paper presented at the 15th ICMI Study: The Professional Education and Development of Teachers of Mathematics, State University of Sao Paolo, Brazil.
Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59, 389–407.
Borich, G. D. (2000). Effective teaching methods. Upper Saddle River, NJ: Merrill.
Carpenter, T. P., Fennema, E., Loef-Franke, M., Levi, L., & Empson, S. (2000). Cognitively guided instruction: A research-based teacher professional development program for elementary school mathematics. Madison, WI: National Center for Improving Student Learning and Achievement in Mathematics and Science.
Carroll, T., & Foster, E. (2010). Who will teach? Experience matters. Washington, DC: National Commission on Teaching for America’s Future.
Ewing, R., & Manuel, J. (2005). Retaining quality early career teachers in the profession: New teacher narratives. Change: Transformations in Education, 8(1), 1-16.
Feldman, A., & Capobianco, B. M. (2008). Teacher learning of technology enhanced formative assessment. Journal of Science Education & Technology, 17(1), 82-99.
Fennema, E., Carpenter, T. P., Franke, M. L., Levi, L., Jacobs, V. R., & Empson, S. B. (1996). A longitudinal study of learning to use children’s thinking in mathematics instruction. Journal for Research in Mathematics Education, 27, 403-34.
Foster, D. (2009). The algebra crisis. Retrieved from The Noyce Foundation website: http://www.noycefdn.org/documents/math/algebracrisis1008.pdf
Franke, M., Carpenter, T., Fennema, E., Ansell, E., & Behrend, J. (1998). Understanding teachers’ self-sustaining, generative change in the context of professional development. Teaching and Teacher Education, 14(1), 67-80.
Franke, M. L., Carpenter, T. P., Levi, L., & Fennema, E. (2000). Capturing teachers’ generative growth: A follow-up study of professional development in mathematics. American Educational Research Journal, 38, 653-689.
Gearhart, M., & Saxe, G. B. (2004). When teachers know what students know: Integrating mathematics assessment. Theory Into Practice, 43(4), 304-313.
Hanushek, E.A., Kain, J.F., O’Brien, D. M., & Rivkin, S. G. (2005). The market for teacher quality. Washington, DC: National Bureau of Economic Research.
Harris, J., Mishra, P., & Koehler, M. (2009). Teachers’ technological pedagogical content knowledge and learning activity types: Curriculum-based technology integration reframed. Journal of Research on Technology in Education, 41(4), 393-416.
Heid, M., & Blume, G. (2008). Technology and the development of algebraic understanding. In M. Heid & G. Blume (Eds.), Research on technology and the teaching and learning of mathematics (pp.55-108). Charlotte, NC: Information Age Publishing.
Herbert, S., & Pierce, R. (2008). An ‘emergent model’ for rate of change. International Journal of Computers for Mathematical Learning, 13(3), 231-249.
Jung, E., & Rhodes, D. M. (2008). Revisiting disposition assessment in teacher education: Broadening the focus. Assessment & Evaluation In Higher Education, 33(6), 647-660.
Kuchemann, D. (2005). Algebra. In K. Hart & D. Kuchemann (Eds.) Children’s understanding of mathematics: 11-16 (pp. 102-119). London, UK: Antony Rowe Publishing Services.
Langman, J., & Fies, C. (2010). Classroom response system-mediated science learning with English language learners. Language & Education, 24(2), 81-99.
Leatham, K. R., Peterson, B. E., Stockero, S. L., & Van Zoest, L. R. (2011). Mathematically important pedagogical opportunities. In L. R. Wiest & T. Lamberg (Eds.), Proceedings of the 33rd annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 838-845). Reno, NV: University of Nevada, Reno.
Mishra, P., & Koehler, M.J. (2006). Technological pedagogical content knowledge: A framework for teacher knowledge. Teachers College Record, 108(6), 1017-1054.
Monk, S. (1992). Students’ understanding of a function given by a physical model. In G. H. E. Dubinsky (Ed.), The concept of function: Aspects of epistemology and pedagogy. Washington, DC: Mathematical Association of America.
Moses, R., & Cobb, C. (2001). Organizing algebra: The need to voice a demand. Social Policy, 31(4), 4-12.
Nathan, M. J., & Koedinger, K. R. (2000). An investigation of teachers’ beliefs of students’ algebra development. Cognition and Instruction, 18(2), 207-235.
Nathan, M. J., & Petrosino, A. (2003). Expert blind spot among preservice teachers. American Educational Research Journal, 40(4), 905-928.
National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common core state standards for mathematics. Washington, DC: Authors.
National Council of Teachers of Mathematics. (2000). Principles and standards of school mathematics. Reston, VA: Author.
National educational technology plan. (2010). Retrieved from the U.S. Department of Education website: http://www.ed.gov/technology/netp-2010
Oregon Department of Education. (2014). Education data explorer. Retrieved from searchable database at http://www.ode.state.or.us/apps/BulkDownload/BulkDownload.Web/
Peterson, B. E., & Leatham, K. R. (2009). Learning to use students’ mathematical thinking to orchestrate a class discussion. In L. Knott (Ed.), The role of mathematics discourse in producing leaders of discourse (pp. 99-128). Charlotte, NC: Information Age Publishing.
Puntambekar, S., Stylianou, A., & Goldstein, J. (2007). Comparing classroom enactments of an inquiry curriculum: Lessons learned from two teachers. The Journal of the Learning Sciences, 16(1), 81-130.
Sarama, J., & Clements, D. H. (2008). Linking research and software development. In G. W. Blume & M. K. Heid (Eds.), Research on technology and the teaching and learning of mathematics: Volume 2, Cases and perspectives (pp. 113-130). New York, NY: Information Age Publishing, Inc.
Sherin, M. G. (2002). A balancing act: Developing a discourse community in a mathematics classroom. Journal of Mathematics Teacher Education, 5(3), 205-233.
Singh, D. K., & Stoloff, D. L. (2008). Assessment of teacher dispositions. College Student Journal, 42(4), 1169-1180.
Smith, M. & Stein, M. (2011). 5 Practices for orchestrating productive mathematics discussion. Reston, VA: National Council of Teachers of Mathematics.
St. George, D. (2014, July 12). Montgomery algebra failures mean some students have to bail on summer plans. Washington Post. Retrieved from http://www.washingtonpost.com/local/education/montgomery-algebra-failures-mean-some-students-have-to-bail-on-summer-plans/2014/07/12/b9cde8ac-00a7-11e4-8572-4b1b969b6322_story.html
Suh, J. M., & Moyer-Packenham, P. S. (2007). Developing students’ representational fluency using virtual and physical algebra balances. Journal of Computers in Mathematics and Science Teaching, 26(2), 155-173.
Thadani, V., Stevens, R. H., & Tao, A. (2009). Measuring complex features of science instruction: Developing tools to investigate the link between teaching and learning. The Journal of the Learning Sciences, 18(2), 285-322.
Voogt, J., Fisser, P., Pareja Roblin, N., Tondeur, J., & van Braak, J. (2013). Technological pedagogical content knowledge—A review of the literature. Journal of Computer Assisted Learning, 29(2), 109-121.
Wells, G., & Arauz, R. M. (2006). Dialogue in the classroom. The Journal of the Learning Sciences, 15(3), 379-428.
Zbiek, R. M., & Hollebrands, K. (2008). A research-informed view of the process of incorporating mathematics technology into classroom practice by inservice and prospective teachers. In M. K. Heid & G. W. Blume (Eds.), Research on technology and the teaching and learning of mathematics (Vol. 1; pp. 287-344). Charlotte, NC: Information Age.
Author Notes
Steve Rhine
Pacific University
Email: [email protected]
Rachel Harrington
Western Oregon University
Email:[email protected]
Brandon Olszewski
Senior Educational Consultant
International Society for Technology in Education
Email: [email protected]
![]()