Several factors may contribute to differential opportunities to learn mathematics and, ultimately, discrepancies between students’ mathematics achievement in the United States and their international counterparts (Mullis, Martin, Foy, & Arora, 2012), as well as between subpopulations within the United States (National Center for Education Statistics [NCES], 2013). One important way to achieve effective mathematics instruction is for individuals to recognize that teaching mathematics well requires substantial knowledge and skill.
To that end, the National Mathematics Advisory Panel (NMAP, 2008) has called for further research “to draw conclusions about the features of professional training that have effects on teachers’ knowledge, their instructional practice, and their students’ achievement” (p. xxi). Thus, the need for a research-based model of teacher professional development (PD) that articulates how to help teachers improve their own and their students’ learning and skills is critical.
The goal of the present study was to investigate the impact of a yearlong, online teacher professional development (oTPD) program, Prime Online, on teachers’ mathematics knowledge for teaching (MKT; Ball et al., 2006; Ball, Thames, & Phelps, 2008) and to examine the components of a PD program that impacted participants’ MKT. This study thus attends to the call for mixed-methods research that not only “answer(s) questions about whether a program design works well but also provide(s) evidence to explain why it works well” (Dede, Ketelhut, Whitehouse, Breit, & McCloskey, 2009, p. 13). Further, it responds to Rourke and Kanuka’s (2009) concern related to the dearth of empirical research that measures learning within a community of inquiry (Garrison, Anderson, & Archer, 2000, 2001, 2010), as it examines the components of an oTPD program to consider their collective impact on participant growth.
This paper presents evidence for the impact of Prime Online, designed to engage participants in mathematics content, instructional strategies for teaching all mathematics learners, and teacher inquiry, through an examination of participants’ growth on two measures of MKT (i.e., Content Knowledge for Teaching – Mathematics; Learning Mathematics for Teaching [LMT], 2001a, 2001b), as well as their statements from focus group interviews. It then presents analyses of program components, both to contextualize these findings and to introduce our initial theorizing about how Prime Online components potentially stimulated growth in MKT. The primary hypothesis of this study is that carefully designed and implemented oTPD can positively impact teachers’ MKT and subsequent student learning.
Teacher Knowledge
A positive relationship exists between teachers’ mathematics content knowledge and student achievement (Hill, Schilling, & Ball, 2004), but the relationship between mathematics coursework taken by elementary teachers and student achievement is less clear (NMAP, 2008; Swars, Hart, Smith, Smith, & Tolar, 2007). MKT is the “mathematical knowledge needed to carry out the work of teaching mathematics” (Ball et al., 2008, p. 395), including evaluating students’ responses, answering students’ questions, creating assignments, and planning lessons, as well as differentiating instruction and communicating with parents and building administrators. Ball et al. (2008) likened the tasks related to effective mathematics instruction to Kilpatrick, Swafford, and Findell’s (2001) mathematical proficiency and stated that teachers of mathematics need to know “more, and different, mathematics” (p. 396), such as error analysis, recognition of alternative strategies as valid, and conceptual understanding of algorithms.
Unfortunately, Grades 3-5 teachers are less likely to have strong mathematics backgrounds and are more likely to hold negative perceptions of their own experiences as mathematics learners that can have lasting effects on how teachers “interpret their mathematical worlds” (Philipp, 2007, p. 258). Few of these teachers received preservice mathematics education courses designed to help them—and ultimately their students—achieve deeper, more meaningful learning, such as analyzing mathematical arguments for accuracy and determining whether an alternative strategy will accurately reach problem solutions all of the time (Ball et al., 2008).
Teacher Professional Development
Historically, teacher PD programs have offered “fragmented, intellectually superficial” seminars (Borko, 2004, p. 3) that have not provided ongoing guidance for teachers as they attempt to learn and change their practices (Barnett, 2002). The National Survey of Science and Mathematics Education (NSSME; Banilower et al., 2013) indicated that, while 87% of elementary teachers surveyed reported participating in PD within the 3 years prior to the study, only 11% of these experiences were substantial (i.e., more than 35 hours). Seventy percent of the respondents reported experiencing less than 15 hours of PD within the previous 3 years.
This finding echoes earlier findings by Hill (2007), who reported that most mathematics education PD programs across the country are characterized by one-time workshops providing disjointed and ill-conceived instructional activities. In fact, 91% of Banilower and colleagues’ (2013) participants indicated that they attended a single-day “workshop” on mathematics or mathematics teaching. As Hill noted, “By all accounts, professional development in the United States consists of a hodgepodge of providers, formats, philosophies, and content” (p. 114).
Several investigators have provided recommendations for effective PD that goes beyond the one-time workshop (e.g., Garet, Porter, Desimone, Birman, & Yoon, 2001; Marrongelle, Sztajn, & Smith, 2013) to move toward long-term “serious and sustained learning of curriculum, students, and teaching” (Ball & Cohen, 1999, p. 4). Effective PD may be characterized as engaging participants in collaborative examination of curriculum, participating in investigations of mathematics content, investigating students’ responses to mathematics content, reflecting on their efforts to implement instructional strategies within their classrooms, developing collaborations between practitioners and university personnel, and recognizing teachers as professionals (Garet et al., 2001; Hill, 2004; Lee, 2005; Little & McLaughlin, 1993; Marrongelle et al., 2013).
Desimone (2009) described core features of effective PD to include content focus, active learning, coherence, duration, and collective participation. Similarly, Scher and O’Reilly’s (2009) meta-analysis resulted in three components of effective PD interventions: duration, content, and form. Finally, Marrongelle et al. (2013) included the design of materials
that explicitly address the mathematics content and practices of the Common Core State Standards for Mathematics (CCSSM; National Governors Association Center for Best Practices & Council of Chief State School Officers [NGACBP & CCSSO], 2010) and provide vivid images of teaching and learning that are consistent with CCSSM. (p. 206)
Fewer than half of the teachers who responded to the 2012 NSSME (Banilower et al., 2013), however, reported experiences that reflected these best practices in PD. This circumstance is compounded by the fact that 58% of these teachers reported taking two or fewer of the five college-level mathematics courses recommended by the National Council of Teachers of Mathematics (NCTM; i.e., number and operation, algebra, geometry, probability, and statistics; Banilower et al., 2013, p. 18).
Findings from the limited number of studies that inform the content focus of PD in mathematics suggest that when both content and pedagogy are included as part of the PD, the intervention has a greater potential for positive impact on student achievement than when the PD is focused on content or pedagogy only (Hill, Rowan, & Ball, 2005). Little is known about the actual content of PD programs or how this content may influence teacher knowledge and behavior. Hill and Ball’s (2004) study, however, suggested that when teachers were (a) engaged in mathematical analysis, (b) explored alternative representations, and (c) communicated explanations and connected ideas with other teachers and PD facilitators, positive influences on teachers’ content knowledge for teaching mathematics were found. Given these recommendations, the Prime Online oTPD program was developed to focus on both mathematics content and pedagogy and on active teacher participation within a community of learners over a sustained time period.
Online Teacher Professional Development and Community of Inquiry
We developed Prime Online based not only on the literature related to mathematics teacher knowledge and professional development that supports teacher knowledge growth but also on the literature related to online learning and oTPD. The online nature of the program responds to many calls for PD that “fit(s) teachers’ busy schedules, that draws upon powerful resources often not available locally, and that can provide real-time, ongoing, work-embedded support (that) has prompted the creation of online teacher professional development programs” (Whitehouse, Breit, McCloskey, Ketelhut, & Dede, 2006, p. 13). Online programs are essential to teachers’ development, especially when considering scale or reaching those teachers who live and work in rural areas and have limited access to PD.
Various affordances of oTPD include high-quality learning opportunities, access to experts at low costs to districts, ample time to reflect prior to interaction, flexibility for teachers who have busy work lives, and personalized learning spaces (Dede et al., 2009; Sprague, 2006). Benefits of online mathematics courses have been noted to include (a) a wide range of potential resources; (b) convenience, flexibility and accessibility, which is especially important to teachers who have busy schedules and may not be able to attend face-to-face learning opportunities; (c) a dynamic learning environment; (d) varied communication opportunities; (e) the potential for individual and independent learning; and (f) the facility with which today’s students may engage in these learning opportunities (Engelbrecht & Harding, 2005a, pp. 264-266). High-quality online learning opportunities are active, problem-based, and learner-centered with multiple ways of communicating within reflective spaces where modeling is possible (Mayes, Ku, Akarasriworn, Luebeck, & Korkmaz, 2011).
Online learning has evolved with changes in both technology and pedagogical perspectives that reflect a paradigm shift in education to a distributed model emphasizing a constructivist perspective on teaching and learning (Anderson & Dron, 2011; Engelbrecht & Harding, 2005a). While the first generation of online learning environments emphasized a cognitive-behavioral perspective, constructivist and connectivist perspectives have influenced more recent programs (Anderson & Dron, 2011). These latter generations emphasize group and networks as the focus of learning rather than the individual.
Many elementary teachers lack conceptual knowledge and deep understanding of mathematics (Ball, Sleep, Boerst, & Bass, 2009), which makes online learning of mathematics even more challenging. Maximal benefit may be realized when teachers have some level of mathematical knowledge or a “specific readiness” in mathematics (Ponte & Santos, 2005). While constructivist paradigms predominate in online learning,
providing structured ways of collaboration and solving problems is probably more appropriate….Care should be taken to have a sound balance between teacher and learner-centered activities and that interaction should be carefully planned; interaction between learner and content, between learner and instructor and between learner and learner. (Engelbrecht & Harding, 2005b, p. 254)
Thus, when considering oTPD environments for elementary teachers of mathematics, it is critical to consider the aspects of the environment that increase their interactivity and persistence.
A conceptual framework that has gained increasing prominence within the online learning literature is the community of inquiry framework (Garrison, 2006, 2013; Garrison et al., 2000, 2001, 2010). According to this perspective, learning is a constructive endeavor that occurs through three essential elements (i.e., cognitive, social, and teaching presence).
Cognitive presence is “the extent to which the participants in any particular configuration of a community of inquiry are able to construct meaning through sustained communication” (Garrison et al., 2000, p. 89). Within an online context, students may interact less than in a face-to-face environment, but these interactions are preceded with significant reflection, which increases their meaningfulness, is indicative of more critical thinking, and leads to deeper learning. These interactions are predicated on the participants’ social presence or their ability “to project their personal characteristics into the community, thereby presenting themselves to the other participants as ‘real people’” (Garrison et al., 2000, p. 89).
Finally, a crucial component in the construction of a community of inquiry is the instructor. According to Garrison and colleagues (2000, 2001), teaching presence is developed through three general functions of the instructor. First, the instructor is tasked with the design of the learning environment and experiences, including “selection, organization, and primary presentation of course content, as well as the design and development of learning activities” (p. 90). Second, the instructor’s role in facilitating the participants’ interactions with the content is critical and may be more influential than interactions with peers (Swan & Shih, 2005). A third component of teaching presence, direct instruction, relates specifically to instruction on how participants contribute within the online learning environment and is correlated with students’ perceptions of their learning (Shea, Li, & Pickett, 2006).
Garrison et al. (2001) postulated four phases of practical inquiry that are essential for the development of cognitive presence. First is a triggering event that is typically initiated by the instructor but may be introduced by one of the participants. The teacher’s role is to shape the discussion by establishing or redirecting the triggering event. Participants engage in the reflective process as they enter the exploration phase during which they are determining the problem as they move between individual reflection and social exploration of the triggering event. This phase may include such cognitive processes as brainstorming, questioning, and exchanging information.
During the third phase, integration, the participants are “constructing meaning from the ideas generated in the exploration phase” (Garrison et al., 2001, p. 10). Teaching presence is important to “diagnose misconceptions, to provide probing questions, comments, and additional information in an effort to ensure continuing cognitive development, and to model the critical thinking process” (p. 10). Finally, during resolution, the fourth phase, the participants are enacting their solution frequently within a practical application.
Social presence and learner satisfaction have been linked (Swan & Shih, 2005) and are essential for cognitive presence leading to deep and meaningful learning (Garrison et al., 2000, 2001, 2010). Factors found to increase social presence and learner satisfaction include media integration and quality of instruction, which was a proxy for teaching presence and operationalized as the instructor’s ability to explain content, to motivate students, and to provide feedback (Kim, Kwon, & Cho, 2011).
As it relates to teaching presence, factors that increase social presence and learner satisfaction include courses designed to offer choices of activities linked to media resources, facilitate discussion with timely feedback, create a space for students to share their personal stories and to feel valued for contributions, and guide successful interaction and completion (Kim et al., 2011). Finally, Shea and colleagues (Shea et al., 2006; Shea, Li, Swan, & Pickett, 2005) examined the development of community within online contexts providing some evidence for the relationship between teaching presence and community.
Studies that have examined learning within the community of inquiry framework have been criticized for methodological issues including vague, one-question surveys of students’ perceptions of learning (Rourke & Kanuka, 2009). The present study provides evidence of learning by examining participants’ MKT through a validated measure and their reports of learning within focus group interviews. It then begins to theorize about factors that may have supported participants’ MKT growth within the community of inquiry framework.
Context of the Study
The Prime Online oTPD program was developed as the result of a collaborative effort between three teacher educators and researchers with expertise in special education, mathematics education, and teacher professional development with a focus on teacher inquiry. The present study reflects the second year of the larger 3-year research project with two separate cohorts of teachers funded by the U.S. Department of Education’s Institute of Education Sciences. This yearlong, asynchronous oTPD program included 35 modules organized within three integrated segments of content and pedagogy. The purpose of the program was to impact teachers’ MKT and instruction targeted at learners who struggle to learn mathematics, including students with learning disabilities.
The first segment (9 weeks, June-August), Building the Foundation for Inclusive Elementary Mathematics Classrooms, engaged participants in discussions related to the NCTM (2000) Vision of School Mathematics, mathematics proficiency (Kilpatrick et al., 2001; Suh, 2007), characteristics and learning problems of students with learning disabilities (e.g., Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007), foundations of instructional decision-making and assessment practices (e.g., Ysseldyke & Tardrew, 2007), and foundations of evidence-based practice in mathematics for students with learning disabilities (e.g., Miller & Hudson, 2007). This segment provided introductory information to orient participants to the overarching perspectives of Prime Online, including culminating sessions that introduced them to the process of teacher inquiry (Dana, 2013; Dana & Yendol-Hoppey, 2009, 2014).
The content of the second segment (13 weeks; September-December), Deepening Mathematics Content and Pedagogy, was aligned with the CCSSM (NGACBP & CCSSO, 2010) for Grades 3-5, including number sense, whole and rational numbers, and mathematical operations with whole numbers and rational numbers. The goal of this segment was to engage participants in activities that supported their developing mathematics content knowledge and instructional practices that support all learners, but particularly students with learning disabilities.
The third, culminating segment (13 weeks, January-April), Studying the Application of Newly Learned Mathematics Content and Pedagogy to Student Learning, engaged learners in the inquiry process (Dana, 2013; Dana & Yendol-Hoppey, 2009, 2014) as they worked to examine student understanding and implement the instructional practices that were learned during the first two segments. Both the introductory material in Segment 1 and the inquiry in which participants engaged during Segment 3 likely also supported participants’ developing MKT, but Segment 2 activities were the focus of the present analysis.
Segment 2, Building Conceptual Knowledge for Teaching
Because the focus of the current study is on Segment 2 of Prime Online, this paper presents a more detailed discussion of the ways in which activities were combined to support participants’ knowledge construction with an emphasis on cognitive, social, and teaching presence (Garrison et al., 2000, 2001). The example that follows focuses on the module for Week 19, Multiplication of Fractions. All three segments of Prime Online were developed with 1-week modules and a consistent format including four components: (a) Introduction, (b) Anticipatory Activity, (c) Content and Discussion, and (c) Classroom Connections.
The Introduction provides participants with an overview of the week’s activities, goals and objectives, and reference materials needed to complete the learning tasks to facilitate participants’ navigation through the week and completion of the activities. The second component, the Anticipatory Activity, elicits participants’ prior knowledge, prepares their thinking to set the stage for the content they explore in the module, and frequently served as a triggering event (Garrison et al., 2001).
We typically engaged participants in mathematics by asking them, for example, to represent a concept such as an arithmetic operation (Figure 1) or a rational number (Figure 2). Alternatively, participants were provided a fictitious students’ mathematical thinking or error to examine.
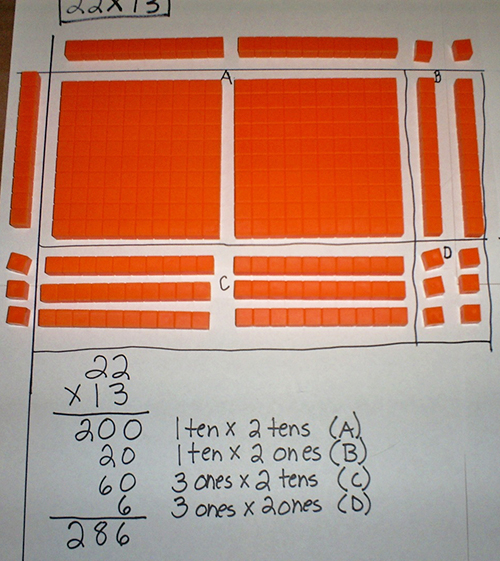
Figure 1. Multiplication with base-10 blocks using an area model (Week 12, Anticipatory Activity, Participant 129).

Figure 2. Representations of “one and three quarters” (Week 16, Anticipatory Activity, Participant 117).
By asking participants to think about the mathematics concept they would be studying in the Content and Discussion component in a way that was different from the typical algorithm or representation (i.e., represent a rational number pictorially using multiple models, Figure 2), these activities supported their engagement with this subsequent material or triggered their thinking about their own mathematical processes for the exploration phase (Garrison et al., 2001). For example, see the Anticipatory Activity for Week 19, Multiplication of Fractions (Figure 3).
| In this activity, we shift from using representations to support students’ understanding of operations to estimation. Estimation can be used to support students’ thinking about the reasonableness of their answers and indicates students’ ability to flexibly work with operations with rational numbers. Estimate the following operations without use of pen and paper or other materials. In the forum, explain the strategy you used to estimate several of these problems. 3 1/4 + 2 1/5= Return to this forum and examine the strategies your colleagues used. Which strategies were interesting to you? Which were different from what you used to solve these problems? How were the strategies different? Over this week, engage one or more of your students with problems similar to the problems noted above. Use appropriate numbers and operations for your grade level. In the Classroom Connections forum, you will be asked to discuss your students’ strategies when using estimation to think about solutions to computation problems. |
| Figure 3. Anticipatory activity for Week 19. |
In this activity, participants were engaged in mathematics and used the discussion forum to create posts about their strategies, while engaging with the mathematics and the similarities and differences between the strategies used by their colleagues. By sharing their strategies the participants increased their social presence by presenting their thinking to the community and projecting themselves into the community as “real people” (Garrison et al., 2000, p. 89).
Over the week, teachers were asked to examine the variety of strategies presented by their colleagues and also to present the Anticipatory Activity problems to their students, examining their strategies as well. The ensuing discussion provided a context in which participants analyzed each other’s thinking to deconstruct a mathematics concept and created an opportunity to develop social presence.
The Content and Discussion section typically introduced participants to the mathematical content of the module. This introduction was often in the form of reading professional or developer-constructed materials and was typically followed by discussion questions, which served the purposes of exploration and integration (Garrison et al., 2001). As the program included NCTM membership for each participant, these materials were often articles from Teaching Children Mathematics or an activity from Illuminations found on the NCTM website (NCTM.org). In addition, the research team created PowerPoint electronic slideshow presentations and other instructional documents to provide content for the teachers.
During Week 19 the participants read and worked through various activities in Philipp and Vincent’s (2003) article, “A Fifth-Grade Student Reflecting Upon Learning Fractions Without Understanding.” In this article, the authors considered the impact of teaching fraction computation from the perspective of learning with or without conceptual understanding. Video clips of student interviews supported participants’ engagement with the concept of teaching with understanding, as they also continued to examine each other’s thinking as well as their students’ strategic behaviors with the same problems from the Anticipatory Activity.
A second activity within the Content and Discussion component of the module asked participants to reflect on two questions as a prelude to subsequent activities across several weeks:
Why do we multiply fractions (or decimal numbers) by multiplying the numerators together and multiplying the denominators together? a/b x c/d = (a x c)/(b x d)
Why do we need common denominators when adding fractions (or decimal numbers) but we don’t need common denominators to multiply two fractions?
Again, these forum discussions were meant to engage participants in thinking deeply about the fundamental underlying mathematics that they were teaching within their Grades 3-5 classrooms.
Finally, during the Classroom Connections portion of the module, participants reflected on their engagement with the content, often within the context of implementing an activity or instructional strategy within their classroom, which in many cases served as the context for resolution (Garrison et al., 2001). For example, participants reflected on their implementation of the content with a small group of students or, when possible, the whole class. This activity, again, was in service of their mathematics learning as they analyzed the ways in which students engaged with the mathematics concepts. (See the Week 19 prompt for the Classroom Connections in Figure 4.)
| In the Anticipatory Activity for this week, we considered how estimation can be used to support students’ thinking about the reasonableness of their answers and to indicate students’ ability to flexibly work with rational numbers and operations on rational numbers. You were asked to engage a student or several students with problems similar to the problems in the Anticipatory Activity and to examine your students’ strategies for estimating operations with rational numbers. Your students’ strategies provide a window into their thinking. Problems from the Anticipatory Activity are listed below: 3 1/4 + 2 1/5= In this Classroom Connections forum, create a post in which you (1) describe your student’s or students’ strategies for using estimation to think about solutions to computation problems, and (2) discuss your response to the following question: What do your students’ strategies tell you about their number sense relative to operations with rational numbers? |
| Figure 4. Week 19 prompt for the Classroom Connections. |
At the end of each week, a facilitator announcement was posted to summarize, analyze, and synthesize the participants’ discussions and their collective learning for the week. This summary provided the teaching presence to further stimulate participants’ cognitive engagement with the week’s material.
This example from the Week 19 module within Segment 2, Multiplication of Fractions, provides a detailed description of the nature of the content and pedagogy found within each module. Given this overview of Prime Online and specific information regarding Segment 2, the research questions for the current study were as follows:
- What was the impact of Prime Online on participating teachers’ MKT?
- What are the characteristics of the activities provided to support changes in participants’ MKT?
Method
Participants
Twenty-three Grades 3-5 teachers from an initial group of 32 teachers participated in Prime Online. Nine teachers left the study before completing Segment 1. The remaining participants included 17 elementary general education and 6 special education teachers from 18 schools in 14 school districts across one southeastern US state. Ninety-one percent (n = 21) were female, with the same proportion indicating their ethnicity as White. Two (8.7%) participants identified as Hispanic.
Among the teachers who indicated their primary responsibilities within a regular education classroom, 1 (4.4%) participant taught third grade, 9 (39.1%) taught fourth grade, 6 (26.1%) taught fifth grade, and 1 taught a combination fourth- and fifth-grade class. In addition, 6 participants taught special education, with equal numbers (13.0%) indicating K-5 and 4-5 grade levels as their primary responsibility.
Participants’ years of teaching experience ranged from 2 to 38, with a mean of 11.7 years (SD = 9.6) and with over 78% of the sample reporting 6 or more years of experience. Finally, 87.0% of teacher participants (n = 20) reported prior online learning experience.
Data Sources
Two sources of data (quantitative and qualitative) were analyzed to provide evidence for the efficacy of Prime Online in terms of growth within participants’ MKT. Participants completed two of the Content Knowledge for Teaching Mathematics (CKT-M) scales: Elementary Number Concepts and Operations-Content Knowledge (CK; LMT, 2001a) and Elementary Number Concepts and Operations-Knowledge of Content and Students (KCS; LMT, 2001b). Each of these measures has three equated forms that include between 18 and 26 multiple-choice items assessing teachers’ mathematics knowledge.
These assessments were designed to measure teachers’ MKT across a variety of tasks, such as error analysis, multiple representations, estimation, and invented strategies (Hill et al., 2004). These authors reported adequate reliability estimates ranging from .62 to .78. A secondary source of data, teacher focus group interviews, provided additional self-report evidence of the impact of the program on teachers’ MKT. Second, to contextualize changes in participants’ MKT, the activities within each component of the Segment 2 Modules 10-22 were analyzed to describe the components and activities developed to impact participants’ MKT.
Procedure
Data collection. CKT-M measures (LMT, 2001a, 2001b) were administered three times: as a pretest prior to the oTPD program (i.e., May), midprogram test after Segment 2 (i.e., December/January), and posttest after Segment 3 (i.e., May). All 23 teachers completed both subtests of the CKT-M at pretest and posttest. At the midprogram data collection, 20 teachers completed the CK subtest and 22 completed the KCS subtest. They completed the online measures within the program’s learning management system in one sitting at a place and time convenient for them. In addition, the project’s external evaluator conducted focus group interviews twice across the 1-year PD program. These interviews were conducted in synchronous, online sessions with small groups of participants.
Data analysis. Data analysis was conducted using a three-step process. First, the CKT-M (LMT 2001a, 2001b) data were analyzed to provide evidence of changes in participants’ MKT. Participants’ number of correct scores was transformed to equated scores using equating tables provided by LMT (2004). In the sample used for equating, the transformed scores had a mean of approximately 0.00. Descriptive statistics were calculated to characterize participants’ knowledge across assessment occasions (Table 1).
Table 1
Descriptive Statistics for CKT-M Measures by Occasion
Occasion | CK | KCS | ||||
M | SD | α | M | SD | α | |
| Pretest | -0.03 | 0.70 | 0.67 | 0.04 | 0.71 | 0.54 |
| Midtest | 0.21 | 0.73 | 0.57 | 0.44 | 0.89 | 0.69 |
| Posttest | 0.47 | 1.07 | 0.81 | 0.02 | 0.51 | 0.56 |
Reliability for each time period ranged from .57 to .81 for the CK measure and .54 to .69 for the KCS measure (Table 1). A frequently cited standard for acceptable alpha coefficients is .70 (Nunnally, 1978), suggesting the alpha levels are low for several subtests and occasions. Due to the missing scores at the midprogram test (three for CK and one for KCS), full information maximum likelihood estimation (FIML; Enders, 2010) was used to estimate means and standard deviations. FIML uses all available scores at each occasion in the estimation. Comparison to estimates computed using typical formulas for means and standard deviations applied separately to the data from each occasion showed the FIML, which affected only the estimates at the midprogram occasion, had a small effect on the estimates.
Latent growth modeling across the three time points was used to examine knowledge growth over the course of the 1-year oTPD program with the three occasions coded as 0, 1, and 2. FIML with robust standard errors was used to estimate parameters and test hypotheses in the latent growth curve analysis. Robust standard errors correct inferential tests for nonnormal distributions. Comparison to results obtained by using FIML without robust standard errors indicated using both procedures would draw the same conclusions.
Next, we analyzed the focus group data to gain further understanding of the results from the quantitative analyses and to provide a context from the participants’ perspective. The external evaluator transcribed the audiorecorded focus group interviews, maintaining the participants’ anonymity to the research team, and presented the research team with a written final report. The external evaluator examined the transcripts using a grounded analysis methodology (Corbin & Strauss, 2008) and determined themes across the focus groups. The themes were presented as assertions that were substantiated by participants’ statements. The research team examined these reports for additional evidence that signified changes in participants’ MKT and to provide examples from the participants’ statements regarding components that supported their change in MKT.
Third, the research team analyzed the module content in several phases to provide context for and explain the nature of the oTPD that may have led to growth in participants’ MKT. First, a research assistant examined the modules to provide initial descriptions of the activities. Next, analytic memos were created as the module content, and initial descriptions were examined in subsequent rounds of analysis to gain insight and generate initial concepts (as in Corbin & Strauss, 2008, p. 140). These initial broad categories were examined further within module component (i.e., Anticipatory Activity, Content and Discussion, and Classroom Connections) to characterize the activities within each of the broad categories and to examine patterns within module components.
Results
The results will be described in two sections: (a) changes in MKT as evidenced in participants’ scores on two subtests of the CKT-M and in their reflections of their learning from the focus group interviews; and (b) a discussion of the types of activities in Segment 2 that afforded the participants opportunities to engage in mathematical thinking and potentially resulted in growth in MKT, with an emphasis on their potential for creating social and cognitive presence (Garrison et al., 2000, 2001).
Content Knowledge for Teaching-Mathematics
The scores on each of the CKT-M measures were transformed to equated scores using equating tables provided by LMT (2004), with a mean of approximately 0.00 (Table 1). The pretest Prime Online mean score on the CK of -0.03 (SD = 0.70) increased to 0.21 (SD = 0.73) from pretest to midtest and by approximately the same amount from midtest to posttest (M = 0.47, SD = 1.07).
Similarly, the teachers’ scores on the KCS increased from pretest (M = 0.04, SD = 0.71) to midtest (M = 0.44, SD = 0.89) following Segment 2. Their mean score on this measure decreased, however, to pretest levels at postadministration (M = 0.02, SD = 0.51).
Z-tests were conducted to determine whether the mean CK and KCS scores for this group of participants were significantly different from 0.00, the approximate mean for the test-equating sample. The nonsignificant Z-score for the initial status (Z = -0.21, p = 0.84) on the CK measure indicates that the Prime Online pretest mean score was not significantly different from 0.00 (Table 2). Similarly, the teachers’ initial mean score on the KCS subtest was not significantly different from 0.00 or approximately the mean for the test-equating sample (Z = 0.25, p = 0.80; Table 3).
Table 2
Results of Latent growth Curve Analysis: CK
Initial Status | Growth | ||
Estimate (SE) | Z (p) | Estimate (SE) | Z (p) |
-0.03 (.14) | -0.21 (.84) | .25 (.07) | 3.32 (.00) |
Table 3
Results of Latent growth Curve Analysis: KCS
Estimate (SE) | Z (p) |
| Initial Status | |
.04 (.15) | .25 (.80) |
| Linear | |
.82 (.31) | 2.63 (.01) |
| Quadratic | |
-.41 (.15) | -2.69 (.00) |
Latent growth curve modeling was used to test for significant changes across administrations of the CKT-M. The growth estimate for the CK data of .25 indicates significant linear growth over the yearlong oTPD program (Z = 3.32; p < 0.00; Table 2). That is, participants’ scores continued to grow across the year and in an approximately linear relationship. Given that the KCS mean scores initially increased from pretest to midtest and subsequently decreased to approximately 0.00 (Table 3), a quadratic model was estimated for the initial two time points, and a quadratic model was fitted for the data from the three time points. The significant linear estimate of 0.82 (Z = 2.63; p = 0.01) indicates an increase from pretest to the midtest in a positive direction (Table 1).
The significant negative quadratic growth estimate of -0.41 (Z = -2.69; p < 0.00), however, provides evidence for a quadratic relationship. That is, participants’ scores initially increased from pretest to midtest but later decreased by the postadministration (Table 1).
Teacher focus group self-reflections on learning. The CKT-M data provides evidence for significant growth in participants’ MKT across three time points. A significant increase occurred in participants’ knowledge of students from pretest to midtest but then returned to preprogram levels after Segment 3. Data collected from the teachers within the focus group interviews suggest that by enhancing their own knowledge throughout the oTPD program, they better understood their students’ thinking.
Participants’ statements during the focus group interviews support the assertion that their MKT increased and indicate an interaction between their growth in MKT and their instructional practices. In short, Prime Online may have influenced teachers’ content knowledge for teaching mathematics, in part, because the oTPD provided opportunities for learning to teach toward conceptual understanding. (In the following quotations FG stands for focus group. The number indicates the specific focus group.)
It was so easy to teach fractions the procedural way. It was hard for me to…use drawings, to ask the why questions instead of the how….My kids’ scores are improving. It blows my mind. I let the children focus on inquiry, give them the pieces to the puzzle, and let them figure it out. The last 10 years I taught procedures. It has been a mental shift. (FG1)
I enjoyed the videos and articles from Dr. Pape. I had manipulatives in my classroom and let the kids explore. But I did not use them to teach for better understanding. So much of my learning had been procedural. Using these manipulatives makes conceptual knowledge so much clearer. (FG2)
These statements suggest not only a greater understanding of the mathematics but of instructional strategies that support the development of conceptual understanding.
Within one of the focus group interviews, the participants indicated a sense of pride in their ability to learn new information and to apply this new knowledge to their teaching:
I was proud…I am from the old school. Learning how to do fractions conceptually took a lot more brainpower than I expected. Being able to use those manipulatives and work in new ways with my students – I am proud I could make that change. (FG3)
They also expressed feelings of pride related to their students’ accomplishments:
I am seeing my struggling students have “aha” moments and I haven’t seen that before. During math disagreements, I see student interactions, they are figuring it out for themselves; they are less reliant on me. They are models for each other, and I am seeing a lot of improvements. (FG2)
I am just proud of my increased awareness of building conceptual knowledge AND procedural knowledge. I catch myself all the time trying to build conceptual understanding before teaching the procedure, and I can tell they are benefiting. I love being able to have mathematical conversations where students can speak the vocabulary and walk me through step by step what we are talking about. (From an individual who was not able to attend the focus group sessions but submitted her responses via email.)
We attribute the increased mathematics content knowledge and teachers’ reported ability to support students’ learning conceptually to several characteristics of the oTPD that are the focus of the third analysis for this study.
Segment 2: Module Content Categories
Several categories of activities emerged from our analysis of the modules. The categories are presented in the sequence in which they typically appeared within the modules. Activities within each of the categories may have appeared in any of the module components, and several of the activities spanned all of the Prime Online modules. The combinations of these components and their collective impact are hypothesized to support teachers’ construction of knowledge useful for teaching.
Engage in mathematical modeling. A significant category of activities required participants to engage in mathematics, often in the form of representing or modeling mathematics concepts such as operations with whole or rational numbers. These activities frequently appeared within the Anticipatory Activity to elicit participants’ prior knowledge or to provide a context in which participants could work through mathematical operations in ways that might differ from their typical algorithms.
For example, participants were asked to compute various mathematical operations using traditional algorithms, alternative algorithms, mental computation, or estimation. They were required to take pictures of their products and upload them within the module, where their representations were then analyzed to determine the underlying similarities within their mathematical representations (Figures 5-6). Specifically, the participants uploaded a representation of an area model for multiplication of whole numbers (Figure 5) and fractions (Figure 6).
Cisco mowed 2/3 of the lawn when his father, Pablo, came home. By the time Cisco finished mowing the lawn, his father had raked about 4/5 of the lawn that Cisco mowed while his father was at work. How much of the lawn had been raked when Cisco finished mowing? How much of the lawn did Cisco and his father still have to rake?
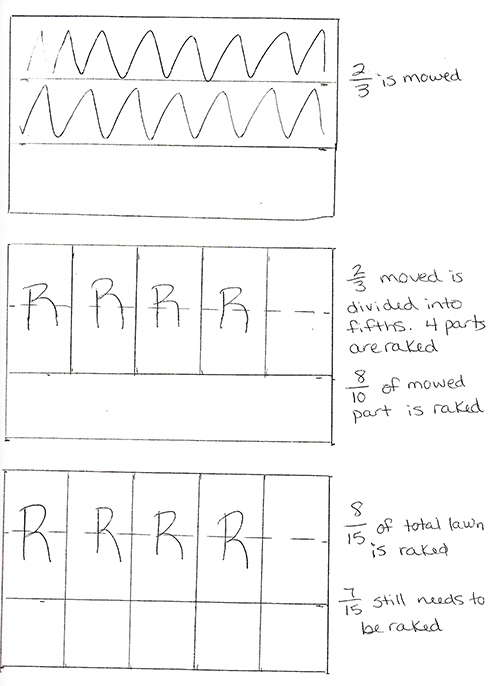
Figure 5. Problem and representation (Week 20, Content and Discussion, Participant 110).
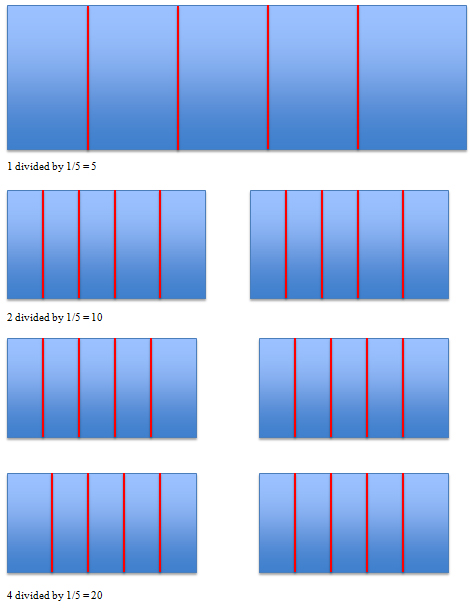
Figure 6. Participant representations for developing conceptual foundation for division of rational numbers (Week 21, Content and Discussion, Participant 116)
These activities were then followed by a discussion that required teachers to first state the strategies they used or provide an explanation of their representation and then compare the other teacher participants’ strategies, looking for commonalities and differences among the ways in which different individuals carried out the processes. These activities sought to engage the participants in the underlying meaning of the mathematics operations, as well as the connections between the same operations with whole and rational numbers.
A final activity within this category required participants to engage in an alternative algorithm (e.g., partial products for multiplying whole numbers or division with fraction using common denominators), followed by using this same algorithm with their students and discussing their students’ experiences with an alternative algorithm. Since these activities were typically within the Anticipatory Activity and provided teachers with opportunities to work through mathematical concepts, they often served as triggers for the exploration of the concepts in subsequent components of the module.
Engage with professional materials. Following these trigger activities (Garrison et al., 2001), the participants were provided materials through which they would explore the mathematics concept. Thus, another significant category of activity engaged participants with professional materials such as Teaching Children Mathematics journal articles, commercially developed videos (e.g., IRIS center, MathVIDS), or web-based applets such as those that may be found on the NCTM Illuminations website. These activities typically appeared in the Content and Discussion component of the modules and were followed by participants’ reflections in online forum discussion posts, which focused on the module content as it might be implemented within participants’ classrooms or ways the material might support mathematical proficiency.
Frequently, participants were asked to compare the recommended practices discussed within materials such as Institute for Education Sciences Practice Guides to their present instruction (i.e., Assisting Students Struggling with Mathematics: Response to Intervention [RtI] for Elementary and Middle Schools, Gersten et al., 2009, and Developing Effective Fractions Instruction for Kindergarten through, 8th Grade, Siegler et al., 2010).
Finally, participants were asked to use an applet that they had engaged with as an adult learner with several of their students. This was typically conducted in an interview format to elicit their students’ thinking or with their whole class as an aspect of instruction. These applications may support integration and resolution (Garrison et al., 2001), as they provided the participants with opportunities for practical applications within their classrooms to further solidify their learning through action.
Engage with researcher-developed materials. The next most prevalent type of activity during the Content and Development component engaged participants in some form of researcher-developed materials, such as an electronic slideshow presentation or document that provided an explanation of the conceptual foundation for a mathematics concept or operation. For example, in one series of documents and video-recorded presentations, the first author explicitly supported the participants’ construction of the foundation for operations with rational numbers. These activities asked participants to engage with manipulative materials as they worked through a sequence of steps to construct the meanings of these operations, which likely increased cognitive presence.
In another video, the first author explicitly engaged participants in the meaning of each of the steps for the division algorithm. These researcher-developed activities were frequently followed by reflective forum discussions similar to those discussed earlier for the commercially developed materials. For example, after the participants watched the video related to division of whole numbers, they were required to engage a small group of students with manipulative materials as they had engaged with the materials while viewing the video. Again, after engaging their students with this activity, participants were asked to discuss the experiences with their peers in the oTPD, which was an effort to support participants’ social presence within the program.
Classroom implementation. Throughout the oTPD program, participants were encouraged to implement what they were learning in their classrooms either in the form of an individual, small group, or whole class activity. Because the oTPD program also focused on teacher inquiry and students with learning disabilities, teachers were frequently required to interview a small number of struggling students after they engaged with the PD activities. For example, teachers used a Broken Calculator applet as adult learners and then worked with a small group of students who were asked to think aloud to reveal their mathematical thinking on the same problems. This applet emulates a calculator with limited functioning keys so that the student must figure out other ways to make the same calculation, such as using addition to do multiplication or using other numerical values that break computations up into component computations.
In another instance, they read one of the IES Practice Guides (Gersten et al., 2009; Siegler et al., 2010), reflected on the similarities and differences in these recommendations, and compared them to their present instructional strategies. Finally, they implemented the recommended instructional strategies within their classroom. In another activity, participants were asked to engage students in mental computation within an interview format and reflect on their students’ strategies and errors.
Reflection and discussion. Participants were frequently asked to reflect on their experiences enacting the activities with their students. They engaged in several types of discussions. Several of the activities required participants to reflect upon the similarities and differences between their present instructional strategies and those encountered within written descriptions of instruction or videorecorded instruction.
Similarly, participants were asked to implement an instructional strategy within their classroom and to reflect upon the results in terms of student learning. We termed these implementation and reflection cycles as “mini-inquiry cycles” designed to provide participants with experiences in conducting these cycles on a smaller scale while working with struggling mathematics learners prior to engaging in their culminating inquiry project.
Participants were also often asked to examine a mathematics concept in the form of strategies for estimating arithmetic operations, representations of computational steps, or student error patterns and discuss these approaches in terms of what they reveal about students’ mathematical thinking. Each of these activities along with reflection and discussion provided the participants with the opportunity to introduce their personal characteristics as they discussed their thinking and their interactions with their students. These types of activities likely increased participants’ sense of social presence within the program.
Discussion
Given the growth in MKT, the present study sought to describe the design features and examine the activities of Prime Online that impacted several facets of participants’ MKT. Our intervention was informed by a substantial review of the literature related to effective PD that pointed us to several important factors related to impacting teachers’ MKT. As we developed the modules, we carefully attended to the literature on effective PD for sustained learning and instructional change. Several global features that likely supported participants’ learning are discussed next, followed by more detail of the activities’ and modules’ characteristics.
First, Prime Online is a yearlong oTPD program that engages participants in sustained examination of mathematics content, curriculum, and pedagogy (Desimone, 2009; Scher & O’Reilly, 2009). Second, we supported participants’ examination of their practice by engaging them in teacher inquiry (Dana, 2013; Dana & Yendol-Hoppey, 2009, 2014) within mini-inquiry cycles during Segment 2 and as the major project for the program. Although the focus of a separate analysis (Dana, Pape, Griffin, & Prosser, 2015), participants created an inquiry project paper and presented the work they had completed during Segment 3 as their culminating Prime Online experience. In these projects, many of the teachers continued to analyze deeply their instructional strategies in terms of their potential for facilitating learning.
Third, the extant literature indicates course environment (Tallent-Runnels et al., 2006) as a critical component for effective PD. The Prime Online development team focused on course environment as it was reflected in the online classroom culture, assistance provided, and interactions among participants. We placed particular emphasis on establishing and sustaining a community of learners (Winograd, 2000) and developed a sense of social presence (Garrison et al., 2000) through peer interaction related to participants’ mathematical representations and by establishing norms for effective communication.
To stimulate conversation within the online community, we used guiding questions that fostered participant interaction (Greene & Land, 2000). We incorporated other features shown to increase learning in online contexts, such as communication about mathematical concepts, opportunities for collaboration in the form of discussion groups, and incorporation of Internet resources (e.g., applets and videos; Engelbrecht & Harding, 2005a, 2005b).
Fourth, we specifically focused on creating a community of inquiry (as described by Garrison, 2006, 2013; Garrison et al., 2000, 2001, 2010). According to this theoretical framework, a community of inquiry is predicated on social, teaching, and cognitive presence. We engaged learners in multiple opportunities to do mathematics, followed by explaining their mathematical behaviors and engaging their colleagues in discussion of the similarities and differences in their mathematical thinking. The activities we provided, therefore, potentially support the development of social and cognitive presence as well as learner satisfaction, which have been found to correlate (e.g., Kim et al., 2011; Swan & Shih, 2005). Further, the present study is one of the few studies that have employed a valid measure of learning within the context of the community of inquiry framework (Rourke & Kanuka, 2009).
While these global design features were critical to the success of the oTPD program, the present study attempted to examine the activities more closely for their potential to impact participants’ MKT specifically. Ball, Hill, and colleagues’ (e.g., Ball et al., 2006, 2008) foundational work on the mathematics knowledge needed to teach effectively reveals several important components of MKT, including both subject matter (i.e., Common Content Knowledge and Specialized Content Knowledge) and pedagogical content (i.e., Knowledge of Content and Students and Knowledge of Content and Teaching) knowledge.
Prime Online was developed with the explicit goal of supporting teacher participants’ growth in each of these domains. As our analysis indicates, the module components were designed specifically to challenge participants to learn fundamental mathematics concepts conceptually (Common Content Knowledge and Specialized Content Knowledge) and implement instruction within their classrooms to support students’ conceptual understanding of these concepts (Knowledge of Content and Teaching). They were also challenged to explain their mathematical thinking (Common Content Knowledge and Specialized Content Knowledge), to elicit students’ mathematical thinking as they engaged in mathematics activities (Knowledge of Content and Students), and to collaboratively reflect on these strategies as they revealed students’ mathematical reasoning (Knowledge of Content and Students).
These components aligned with the recommendations put forth in the literature (e.g., Desimone, 2009; Garet et al., 2001; Lee, 2005; Little & McLaughlin, 1993; Scher & O’Reilly, 2009) and have significant potential for increasing participants’ cognitive presence within the program (Garrison, 2006, 2013; Garrison et al., 2000, 2001, 2010). Specifically, the activities (a) engaged participants in mathematical analysis, (b) asked them to think through alternative representations, and (c) required them to communicate their explanations and to examine them for similarities and differences as was recommended by Hill and Ball (2004).
Through our analysis, we have begun a much needed discussion within the literature related to oTPD development that may inform the field as the number of oTPD programs continues to increase. Specifically, we provided several categories of activities that were central to knowledge growth. Engaging participants in mathematical thinking, articulation of strategic behavior, and representation enabled them to first do the mathematics. More importantly, we engaged participants in discussion that elevated the fundamental concepts of mathematics to objects of discourse (e.g., Walshaw & Anthony, 2008).
Participants frequently compared their thinking with others as they engaged in the mathematics and looked for commonality in their thinking. They also examined their students’ mathematical thinking and error patterns and described their interactions with their students, which potentially supported their sense of social presence. These activities provided the teachers with an opportunity to examine mathematical thinking and to learn how to analyze this thinking, which may have contributed to participants’ MKT. Teachers do not frequently have opportunities to do these kinds of analyses within mediated contexts.
In addition to these analyses of mathematics thinking and opportunities to do mathematics, participants were provided content in the form of both commercial and developer-constructed materials. The Internet provides ample opportunities for engaging with interesting videos, applets, websites, and written materials that provide rich learning experiences for the online learner. Incorporating these resources in cycles of engagement with the materials, critical analysis, reflection, and implementation created a powerful context for participant learning.
We also took advantage of NCTM web-based resources, such as articles and applets. For many of the participants this was their first exposure to these resources. In addition, we created similar materials in the form of electronic slideshow presentations, video recordings, and descriptions within developer-constructed materials. The online format facilitated the delivery of this content but also made it critical that these materials were clear and precise.
Each of these significant engagements with mathematical content and the opportunity to discuss their thinking with their colleagues provided structure that potentially supported both social and cognitive presence. Further, the PD providers’ summaries of this thinking and mathematical engagement provided evidence of teaching presence. The combination of these activities, rather than any single component, likely had a collective effect on teachers’ MKT. Further, this evidence supports the assertion that Prime Online was developed to support the critical development of social, teaching, and cognitive presence, which are hypothesized to contribute to the creation of powerful online learning environments.
Finally, challenging participants to implement the activities within their classroom likely supported their knowledge of subject matter as well as pedagogical content knowledge. Examining students’ thinking within clinical interviews provided teachers the context to reflect on the mathematics content from at least three perspectives.
First, the analysis of student thinking revealed underlying fundamental mathematics content. Second, examining how students were thinking about the mathematics content provided a vehicle for learning about their students. Finally, we engaged the participants in several mini-inquiry cycles, which fostered a stance toward learning about their practice within the classroom. This stance not only provided a different perspective on teaching but also provided a context for learning mathematics content.
The decline in participants’ scores on the KCS meaure after Segment 3 was unexpected. This finding is especially troublesome, as this segment is when participants conducted their inquiry project, a task that might be expected to increase or, at least, solidify teachers’ knowledge of their students. One explanation may lie in the low estimates of reliability for this measure, which ranged from .54 to .69 (Table 1). Second, it may be that the singular focus on their students’ learning of a specific mathematics concept during Segment 3, which was the focus of many of the participants’ inquiry projects, did not allow participants an opportunity to solidify this knowledge more broadly.
Most importantly, our project asked the participants to do a great deal. The KCS measure was administered directly following the completion of their inquiry projects and several other surveys. The combination of the inquiry project presentations and write-up and the end-of-program measures may have created participant fatigue that could account for the decline. Likely, the findings result from a combination of factors.
This decline, however, was not supported in the teachers’ statements during the focus group interviews. Additional evidence supports our contention that the participants’ knowledge of their students grew across the program within the teachers’ inquiry projects, which were the focus of a separate investigation (Dana et al., 2015). Dana led our effort to examine the teachers’ inquiry projects and the audiorecorded presentations of these projects for evidence of participants’ mathematical learning.
Two themes emerged in this study. First, teachers were found to “internalize and actualize the general principle of teaching mathematics to support conceptual as well as procedural knowledge” (Dana et al., 2015, p. 12), and they reported developing “better understanding[s] [of] their students’ mathematical thinking” (p. 16). Many teachers designed projects with the intention of engaging their students in activities to develop stronger conceptual understandings of mathematics.
At the end of these projects, teacher participants revealed that the instructional strategies they used positively impacted their students’ learning. The following explanation is representative of the group:
I feel that I was teaching math the same way I was taught math 30 years ago, along with most of the teachers in my school. [We] really only focus on teaching procedures and expect students to memorize basic facts without giving them a conceptual knowledge or teaching them strategies to solve problems.…I now realize that if I take the time to use them [manipulative materials], my students will have better understandings of the concepts. (Participant 5)
In addition, the teachers’ comments provide evidence of greater MKT, as in this teacher’s remark:
Throughout our Prime Online learning, many articles focused on the idea of building solid conceptual learning prior to teaching procedures….After participating in Prime Online, we began to realize that maybe our students could perform procedures, but as far as understanding the “why,” that remained a mystery to most….We needed to incorporate more conceptual knowledge based practice activities for students before introducing any type of procedural work. (Participant 2)
These qualitative data provide convincing evidence that in the teachers’ own judgments, their content knowledge for teaching mathematics, and their understandings of their students’ mathematics thinking were both enhanced throughout the yearlong oTPD program.
Conclusion
A significant need exists to enhance teachers’ knowledge of mathematics content and instruction to address the learning needs of all students and to begin to ameliorate the performance differences between U.S. students and their international comparison groups, as well as between various subpopulations within the United States (Mullis et al., 2012; NCES, 2013). Therefore, educators must better understand the design features of PD programs, especially oTPD programs, that support teachers’ knowledge growth and change instructional practices (Dede et al., 2009).
We created the Prime Online PD program by focusing on both mathematics content and pedagogy for all learners, along with active teacher participation in an online community of learners over one calendar year. This design produced encouraging results for teacher learning. We hold that the benefits of well-designed and implemented oTPD transcend convenience, offering much more to teachers of mathematics than access.
From this study we have learned that Prime Online has potential to provide teachers with ongoing, rigorous, high-quality learning opportunities for impacting their knowledge of mathematics content and pedagogy and of their students. We recommend that future research explore the impact of oTPD on teachers’ classroom environments and instructional practices as well as their students’ mathematics learning.
References
Anderson, T., & Dron, J. (2011). Three generations of distance education pedagogy. International Review of Research in Open and Distance Learning, 12(3), 80-97.
Ball, D. L., Bass, H., Hill, H., Sleep, L., Phelps, G., & Thames, M. (2006, January). Knowing and using mathematics in teaching [PowerPoint slides]. Paper presented at the Learning Network Conference: Teacher Quality, Quantity, and Diversity, Washington, DC. Retrieved from http://www-personal.umich.edu/~dball/presentations/013106_NSF_MSP.pdf
Ball, D. L., & Cohen, D. K. (1999). Developing practice, developing practitioners: Toward a practice-based theory of professional education. In G. Sykes & L. Darling-Hammond (Eds.), Teaching as the learning profession: Handbook of policy and practice (pp. 3-32). San Francisco, CA: Jossey Bass.
Ball, D. L., Sleep, L., Boerst, T. A., & Bass, H. (2009). Combining the development of practice and the practice of development in teacher education. The Elementary School Journal, 109, 458-474. doi:10.1086/596996
Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59, 389-407. doi:10.1177/0022487108324554
Banilower, E. R., Smith, P. S., Weiss, I.R., Malzahn, K. A., Campbell, K. M., & Weiss, A. M. (2013). Report of the 2012 national survey of science and mathematics education. Chapel Hill, NC: Horizon Research, Inc.
Barnett, M. (2002). Issues and trends concerning electronic networking technologies for teacher professional development: A critical review of the literature. Paper presented at the American Educational Research Association, New Orleans, LA.
Borko, H. (2004). Professional development and teacher learning: Mapping the terrain. Educational Researcher, 33, 3-15. doi:17/02/2009 10:37
Corbin, J., & Strauss, A. (2008). Basics of qualitative research (3rd ed.). Thousand Oaks, CA: Sage.
Dana, N. F. (2013). Digging deeper into action research: A teacher inquirer’s field guide. Thousand Oaks, CA: Corwin Press.
Dana, N. F., Pape, S. J., Griffin, C.C., & Prosser, S. K. (2015, April). The role of practitioner inquiry in online professional development for elementary teachers of mathematics: The Prime Online experience. Paper presented at the annual meeting of the American Education Research Association, Chicago, IL.
Dana, N. F., & Yendol-Hoppey, D. (2009). The reflective educator’s guide to classroom research: Learning to teach and teaching to learn through practitioner inquiry (2nd ed.).Thousand Oaks, CA: Corwin Press.
Dana, N. F., & Yendol-Hoppey, D. (2014). The reflective educator’s guide to classroom research: Learning to teach and teaching to learn through practitioner inquiry (2nd ed.).Thousand Oaks, CA: Corwin Press.
Dede, C., Ketelhut, D. J., Whitehouse, P., Breit, L., & McCloskey, E. M. (2009). A research agenda for online teacher professional development. Journal of Teacher Education, 60, 8-19. doi:10.1177/0022487108327554
Desimone, L. M. (2009). Improving impact studies of teachers’ professional development: Toward better conceptualizations and measures. Educational Researcher, 38, 181-199. doi:10.3102/0013189X08331140
Enders, C. K. (2010). Applied missing data analysis. New York, NY: Guildford Press.
Engelbrecht, J., & Harding, A. (2005a). Teaching undergraduate mathematics on the Internet: Technologies and taxonomy. Educational Studies in Mathematics, 58, 235-252. doi:0.1007/s10649-005-6457-2
Engelbrecht, J., & Harding, A. (2005b). Teaching undergraduate mathematics on the Internet: Attributes and possibilities. Educational Studies in Mathematics, 58, 253-276. doi: 0.1007/s10649-005-6457-2
Garrison, D. R. (2006). Online collaboration principles. Journal of Asynchronous Learning Networks, 10, 25-34.
Garrison, D. R. (2013). Theoretical foundations and epistemological insights of the community of inquiry. In Z. Akyol & D. R. Garrison (Eds.), Educational communities of inquiry: Theoretical framework, research, and practice (pp. 1-11). Hershey, PA: IGI Global.
Garrison, D. R., Anderson, T., & Archer, W. (2000). Critical inquiry in a text-based environment: Computer conferencing in higher education. The Internet and Higher Education, 2, 87-105. doi:10.1016/S1096-7516(00)00016-6
Garrison, D. R., Anderson, T., & Archer, W. (2001). Critical thinking, cognitive presence, and computer conferencing in distance education. The American Journal of Distance Education, 15, 7-23. doi:10.1080/08923640109527071
Garrison, D. R., Anderson, T., & Archer, W. (2010). The first decade of the community of inquiry framework: A retrospective. The Internet and Higher Education, 13, 5-9. doi:10.1016/j.iheduc.2009.10.003
Garet, M. S., Porter, A. C., Desimone, L., Birman, B. F., & Yoon, K. S. (2001). What makes professional development effective? Results from a national sample of teachers. American Education Research Journal, 38, 915-945. doi:10.3102/00028312038004915
Geary, D.C., Hoard, M.K., Byrd-Craven, J., Nugent, L., & Numtee, C. (2007). Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Development, 78, 1343-1359. doi:10.1111/j.1467-8624.2007.01069.x
Gersten, R., Chard, D. J., Jayanthi, M., Baker, S. K., Morphy, P., & Flojo, J. (2009). Mathematics instruction for students with learning disabilities: A meta-analysis of instructional components. Review of Educational Research, 79, 1202-1242. doi:10.3102/0034654309334431
Greene, B.A., & Land, S.M. (2000). A qualitative analysis of scaffolding use in a resource-based learning environment involving the World Wide Web. Journal of Educational Computing Research, 23, 151-167.
Griffin, C.C., Dana, N. F., Pape, S. J., Bae, J., Prosser, S., & Algina, J. (2014, April). Prime Online: Teacher professional development for inclusive elementary mathematics classrooms. Paper presented at the annual meeting of the American Education Research Association, Philadelphia, PA.
Hill, H. C. (2004). Professional development standards and practices in elementary school mathematics. The Elementary School Journal, 104, 215-231. doi:0013-5984/2004/10403-0003
Hill, H. C. (2007). Learning in the teaching workforce. The Future of Children, 17, 111-127. Retrieved from http://www.jstor.org/stable/4150022
Hill, H. C., & Ball, D. L. (2004). Learning mathematics for teaching: Results from California’s mathematics professional development institute. Journal for Research in Mathematics Education, 35, 330-351.
Hill, H. C., Rowan, B., & Ball, D. L. (2005). Effects of teachers’ mathematical knowledge for teaching on student achievement. American Educational Research Journal, 42, 371–406. doi:10.3102/00028312042002371
Hill, H. C., Schilling, S. G., & Ball, D. L. (2004). Developing measures of teachers’ mathematics knowledge for teaching. Elementary School Journal, 105, 11-30. doi:10.1086/428763
Kilpatrick, J., Swafford, J., & Findell, B. (Eds.). (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academy Press.
Kim, J., Kwon, Y., & Cho D. (2011). Investigating factors that influence social presence and learning outcomes in distance higher education. Computers & Education, 57, 1512-1520. doi:10.1016/j.compedu.2011.02.005
Learning Mathematics for Teaching. (2001a). Elementary number concepts and operations – content knowledge. Ann Arbor, MI: University of Michigan.
Learning Mathematics for Teaching. (2001b). Elementary number concepts and operations – knowledge of content and students. Ann Arbor, MI: University of Michigan.
Learning Mathematics for Teaching. (2004). Equating and scoring. Ann Arbor, MI: University of Michigan.
Lee, H. J. (2005). Developing a professional development program model based on teachers’ needs. The Professional Educator, 27, 39-49.
Little, J., & McLaughlin, M. (1993). Teacher’s work: Individuals, colleagues, and contexts. New York, NY: Teachers College Press.
Marrongelle, K., Sztajn, P., & Smith, M. (2013). Scaling up professional development in an era of common core standards. Journal of Teacher Education, 64, 202-211. doi:10.1177/0022487112473838
Mayes, R., Ku, H., Akarasriworn, C., Luebeck, J., & Korkmaz, Ö. (2011). Themes and strategies for transformative online instruction: A review of literature and practice. The Quarterly Review of Distance Education, 12, 151-166.
Miller, S.P., & Hudson, P.J. (2007). Using evidence-based practices to build mathematics competence related to conceptual, procedural, and declarative knowledge. Learning Disabilities Research & Practice, 22, 47-57. doi:10.1111/j.1540-5826.2007.00230.x
Mullis, I.V.S., Martin, M.O., Foy, P., & Arora, A. (2012). TIMSS 2011 international results in mathematics. Retrieved from the Boston College website: http://timssandpirls.bc.edu/timss2011/international-results-mathematics.html
National Center for Education Statistics. (2013). 2013 mathematics grade 12 assessment report card: Summary data tables for national and pilot state sample sizes, participation rates, and proportions of SD and ELL students identified. Retrieved from http://www.nationsreportcard.gov/reading_math_g12_2013/files/Tech_Appendix_Math_G12.pdf
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common core state standards for mathematics. Washington, DC: Authors.
National Mathematics Advisory Panel. (2008). Foundations for success: The final report of the National Mathematics Advisory Panel. Washington, DC: U.S. Department of Education.
Nunnally, J.C. (1978). Psychometric theory (2nd ed.). New York, NY: McGraw-Hill.
Philipp, R. A. (2007). Mathematics teachers’ beliefs and affect. In F. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 257-315). Reston, VA: National Council of Teachers of Mathematics.
Philipp, R. A., & Vincent, C. (2003). A fifth-grade student reflecting upon learning fractions without understanding: A video example. Retrieved from the Center for Research in Mathematics and Science Education website: http://www.sci.sdsu.edu/CRMSE/IMAP/pubs/Reflections_on_Fractions.pdf
Ponte, J. P., & Santos, L. (2005). A distance in-service teacher education setting focused on mathematics investigations: The role of reflection and collaboration. Interactive Educational Multimedia, 11, 104-126.
Rourke, L., & Kanuka, H. (2009). Learning in communities of inquiry: A review of research. Journal of Distance Education, 23, 19-48. Retrieved from http://www.ijede.ca/index.php/jde/article/view/474
Scher, L., & O’Reilly, F. (2009). Professional development for K-12 math and science teachers: What do really know? Journal of Research on Educational Effectiveness, 2, 209-249. doi:10.1080/19345740802641527
Shea, P., Li, C. S., & Pickett, A. (2006). A study of teaching presence and student sense of learning community in fully online and web-enhanced college courses. Internet and Higher Education, 9, 175-190. doi:10.1016/j.iheduc.2006.06.005
Shea, P., Li, C. S., Swan, K., & Pickett, A. (2005). Developing learning community in online asynchronous college courses: The role of teaching presence. Journal of Asynchronous Learning Networks, 9, 59-82.
Siegler, R., Carpenter, T., Fennell, F., Geary, D., Lewis, J., Okamoto, Y. … Wray, J. (2010). Developing effective fractions instruction for kindergarten through 8th grade. Retrieved from the U.S. Department of Education Institute for Education Sciences website: http://ies.ed.gov/ncee/wwc/PracticeGuide.aspx?sid=15
Sprague, D. (2006). Research agenda for online teacher professional development. Journal of Technology and Teacher Education, 14, 657-661.
Suh, J. M. (2007). Tying it all up. Teaching Children Mathematics, 14, 163-169.
Swan, K., & Shih, L. F. (2005). On the nature and development of social presence in online course discussions. Journal of Asynchronous Learning Networks, 9, 115-136.
Swars, S., Hart, L. C., Smith, S. Z., Smith, M. E., & Tolar, T. (2007). A longitudinal study of elementary preservice teachers’ mathematical beliefs and content knowledge. School Science and Mathematics, 107, 325-335. doi:10.1111/j.1949-8594.2007.tb17797.x
Tallent-Rennels, M. K., Thomas, J. A., Lan, W. Y., Cooper, S., Ahern, T. C., Shaw, S. M., & Liu, X. (2006). Teaching courses online: A review of the research. Review of Educational Research, 76, 93-135. doi:10.3102/00346543076001093
Walshaw, M., & Anthony, G. (2008) The teacher’s role in classroom discourse: A review of recent research into mathematics classrooms. Review of Educational Research, 78, 516-551. doi:10.3102/0034654308320292
Whitehouse, P., Breit, L., McCloskey, E., Ketelhut, D. J., & Dede, C. (2006) An overview of current findings from empirical research on online teacher professional development. In C. Dede (Ed.), Online professional development for teachers: Emerging models and methods (pp. 13-30). Cambridge, MA: Harvard Education Press.
Winograd, D. (2000, October). The effects of trained moderation in online asynchronous distance education. Paper presented at the annual meeting of the Association for Educational Communication and Technology, Denver, CO.
Ysseldyke, J., & Tardrew, S. (2007). Use of a progress monitoring system to enable teachers to differentiate mathematics instruction. Journal of Applied School Psychology, 24, 1-28. doi:10.1300/J370v24n01_01
Author Notes
The research reported here was supported by the National Center for Special Education Research, Institute of Education Sciences, U.S. Department of Education, through Grant No. R324A100196. The opinions expressed are those of the authors and do not represent views of the U.S. Department of Education. We gratefully acknowledge all the teachers and students for their support and participation in the study.
Stephen J. Pape
Johns Hopkins University
Email: [email protected]
Sherri K. Prosser
University of Florida
Email: [email protected]
Cynthia C. Griffin
University of Florida
Email: [email protected]
Nancy Fichtman Dana
University of Florida
Email: [email protected]
James Algina
University of Florida
Email: [email protected]
Jungah Bae
University of Florida
Email: [email protected]
![]()