Research in teacher professional development has tended to explore impacts of instructional activities on teachers and has focused less on revealing how instructional activities are designed and implemented by mathematics teacher educators (MTEs). Although understanding the impact of instructional activities is important, the development of MTEs’ practices and insights into those practices provide the field with a historical record of scholarly practices (Lee & Mewborn, 2009) and practical knowledge (Arbaugh & Taylor, 2008).
MTEs’ scholarly practices are informed by the research they read and synthesize, while practical knowledge is developed from experiences through reflection. Both scholarly practices and practical knowledge can be shared by MTEs in the form of narratives about practices. Examples of such narratives include the work of Tzur (2001) describing his development as an MTE and the work of Sztajn (2008) describing her understanding of caring relations in professional development. These narratives do not take the form of empirical studies but, rather, unpack particular experiences from practice and describe the impact of and insights from such experiences.
Many more narratives are needed to address “the lack of information on the practice of mathematics teacher educators working with practicing teachers” (Even, 2008, p. 58). Such narratives share the steps and missteps of MTEs as they engage and develop opportunities with teachers and are not meant to be research studies. The emotion and confusion involved in practice is conveyed, and decisions and tensions (Berry, 2007) involved in the work of MTEs are revealed.
Documenting such revelations allows the field of mathematics education to grow in ways similar to those suggested by Thurston (1994) for the field of mathematics. He noted that creating polished proofs did not satisfy the field’s need for personal understanding. Instead, explanations of development of insights are needed. Narratives in mathematics education, like the one shared in this paper, have the power to provide interpretations of what went wrong in practice and why, without blaming the learners or the professional developers.
This paper describes the ways opportunities and constraints in online mathematics teacher education (OMTE) and our view of learning encouraged a deeper consideration of the role of environment in our teaching practice. When online courses were first introduced, like many others, we doubted that such environments could be productively used to support teacher learning. As tools developed and pressure from stakeholders mounted, our curiosity was piqued. Reaching out to teachers far from our campus contexts throughout the school year was inviting and encouraged us to reconsider the possibilities of OMTE.
Literature suggested that possibilities existed in learning and teaching that were afforded only in online environments. In OMTE, design elements capitalizing on online tools contribute significantly to opportunities for development. For example, Sanchez (2011) noted that online dialogs and his understanding of teacher reflection were facilitated by the implementation of an activity called the “note of reflection” (p. 98). These notes focused on possible student responses to a mathematics problem, but the teachers’ dialog, as identified by Silverman (2011), later became a part of the curriculum. Silverman (2012) also explored the nature of participation in such discussions and identified characteristics of participation in online environments that were tied to teacher learning. Encouraging and supporting robust participation and the evolution of discussions in online settings have proven to be challenging. Yet, various facilitation styles have been shown to impact participation and the nature of the dialog in online settings (Lowes, Lin, & Wang, 2007). As mathematics teacher professional development opportunities multiply in online environments, MTEs have begun exploring how to harness the power of the medium and develop learning spaces that foster mathematics teacher development.
Sources recommended to us (e.g., Anderson & Elloumi, 2004) and our local instructional technology personnel encouraged us to develop an environment that was inconsistent with our assumptions about learning. We became committed to building an environment and opportunities for interactions consistent with our views. This paper describes the dissonance that resulted from our attempts to act with a view of learning in mind. The focus is on exploring the role of MTEs in the context of OMTE and the opportunities and challenges they face in that context.
Central to this discussion are our values and the understandings MTEs bring to OMTE and the conflicts between understandings of the online environment and views of learning that undergirded the instructional activities created. This paper does not focus on the mathematics or mathematics for teaching involved in OMTE, but rather on MTEs’ development as teachers in online environments.
Insights shared in this paper were drawn from our first experience with OMTE. Experiences teaching in a new environment or with an unfamiliar population of students provide opportunities for MTEs to learn. Coupled with opportunity is risk, as each curricular and instructional decision has the potential to reveal the teachers’ vulnerabilities and limitations. Yet, sharing narratives about such experiences has the power to inform MTEs’ practices and provoke discussion of such practices.
Our narrative includes the perspective on learning that guides our decision-making, development efforts, and interactions with teachers. The design of each week of a 4-week professional development environment and interactions with the teachers are described. Discussion concludes with recommendations MTEs should consider as they begin building their practices for OMTE.
Constructivist Teachers
Our stance as constructivist teachers guides the design decisions we make and our interactions with learners (Duffy & Jonassen, 1991; Jonassen, 1998). In this section, we briefly define and discuss constructivist teachers and teaching to orient the reader to our view of our practice. This understanding of our teaching is a driving force in interpretations of the productivity of and satisfaction with our practice.
Our meaning for the term constructivist teachers is derived from Steffe and D’Ambrosio (1995):
We call teachers who study the mathematical constructions of students and who interact with students in a learning space whose design is based, at least in part, on a working knowledge of students’ mathematics “constructivist teachers,” and the activity in which they engage “constructivist teaching.” (p. 148)
In the context of professional development for mathematics teachers, our working knowledge of teachers’ mathematics is applied to the design of the learning space for interaction. Our view of teachers’ mathematical knowledge draws from a radical constructivist view of learning and knowledge (von Glasersfeld, 1995). We view knowledge as a collection or web of interrelated schemes and concepts developed through interactions. These schemes are developed to be productive in particular situations and then are triggered in new situations where the schemes are considered, perhaps unconsciously, to be potentially productive.
This means that teachers have schemes and concepts that are triggered by situations in their practice that include noticing (Jacobs, Lamb, & Philipp, 2010) and interpreting children’s mathematics (Steffe, 1990). We do not view understanding of children’s mathematics as held separate and apart from teachers’ mathematics, but rather understand these as integrated or at least interacting as the teacher engages children. This view of mathematics informs our development of instructional activities and our interactions with teachers.
Constructivist teachers “consider other people’s humanity” and strive not to “treat them as objects” (von Glasersfeld, 1995, p. 127). This orientation toward teachers is grounded in our “need for other people in order to establish the intersubjective viability of ways of thinking and acting” (p. 127). Without the teachers, our opportunity to learn about the development of mathematics used in teaching is eliminated. Considerations of power and positioning constrain and inform our practice.
We are aware of our power to position teachers as knowers of mathematics and contributors to discussions of teaching and learning. Concern about who should have the power to direct the attention of the teachers and evaluate their work drives the development of activities and the ways discussions are facilitated. Building rapport with the teachers allows us opportunities to convey our interest in their thinking. Although we have developed practices to build rapport in face-to-face encounters, we have struggled to translate those efforts and actions into the asynchronous online (AO) environment.
In face-to-face interactions we ask many questions rather than commenting on student conversations or activities. One goal of questioning is to encourage students to reflect on their thinking and that of others. A second goal is that students begin asking themselves and others thought-provoking questions. Teachers we have worked with often ask probing questions. When teachers seek guidance from us, we turn these questions back to the group. The teachers then explore the suggestions and insights with little encouragement from us.
The AO environment challenges us to question in ways that honor what has been said and provoke further exploration without positioning any teacher as less knowledgeable or insightful. In face-to-face interactions, questions can be asked using characteristics of space and facial features. An MTE can move closer to a teacher to provide support and comfort or smile to encourage elaboration. Supporting teachers online requires a reinterpretation of the notion of student teacher relationship that serves as the basis for questioning.
Central in the design of learning environments for teachers are our assumptions about engagements and their potential to provoke disequilibrium. We assume that provocations will stem from explorations and discussions of mathematics, students, and mathematics teaching. In interactions with teachers we attempt to maintain a balance of power, building from the idea that learning involves consciously or unconsciously holding one’s own idea alongside a newly introduced idea so that both can be considered (Confrey, 1991; Wilson, Mojica, & Confrey, 2013).
We do not assume that the teachers’ views of learning match our own. Instead, understandings of the learning environment and teachers are used to create opportunities to encourage teachers to compare ideas. We assume such comparisons will lead to accommodations of existing knowledge structures when a new idea is viewed as different and more productive.
The role of listening is central to building learning opportunities for teachers. Davis (1997) described three types of listening: evaluative, interpretive, and hermeneutic. Our assumptions about the teacher as a listener are based on D’Ambrosio’s (2004) reinterpretation of hermeneutic listening and Weisglass’ (1990) constructivist listening. Davis described hermeneutic listening as evidenced by changes in both the teacher and the learner through the listening. D’Ambrosio reinterpreted hermeneutic listening from a constructivist perspective, noting that the teacher listens to and interacts with the learner as a learning collaborator or a colearner. While what is being learned by the learner and the teacher may be different, both are engaged in learning. Teachers work to act in alignment with learners to gather evidence of learners’ knowledge structures and realize that this effort may result in opportunities for their own learning. Further, teachers realize that as they interact they will consider new and unique ways to engage and provoke learners.
We assume an additional dimension of listening, that of constructivist listening, as originally described by Weissglass (1990). Constructivist listening involves the listener as supporting the creative work of the talker. In teaching and learning, constructivist teachers listen to gather information but also to support learners to explore and represent their ideas as they are being formed. Constructivist listeners encourage learners to explore their own ideas with talk in the hope that the representations generated lead to insights and ideas. For us, this meant that professional developers assume the role of listeners with silent attention and encouragement.
These perspectives ground the design of learning spaces we construct that have the potential to promote teacher professional development. As we began to envision an online professional development experience, these understandings of our practices informed our work.
Content and Design of the Module
The 4-week professional development experience in the AO environment was designed to provide teachers with an opportunity to explore proportional reasoning for teaching. In addition, we reasoned that the environment would allow us to gain further insights into proportional reasoning for teaching. Our view of proportional reasoning is drawn from Vergnaud’s (1994) multiplicative conceptual field.
This view, coupled with findings about children’s proportional reasoning (e.g., Lamon, 1994; Lobato & Ellis, 2010) and teachers’ use of proportional reasoning in teaching (Dole, Clarke, Wright, Hilton, & Roche, 2008; Lobato, Orrill, Bruken, & Jacobson, 2011; Watson, Callingham, & Donne, 2008), formed the basis for the content of the professional development activities and experiences we designed. Activity formats such as tasks analysis, explorations of student work, and selection of student work for classroom discussions (Brown & Clark, 2006; Cameron, Dolk, Fosnot, & Hersch, 2005) provided a design frame for the professional development content. We had designed and productively used such activities in face-to-face professional development.
In the designing the module, we considered teachers’ incentives to participate. Although teachers in AO environments are often rewarded or provided with incentives such as a stipend or course credit, teachers who participated with us were volunteers. No course credit or rewards were offered to them. We designed the module with this dynamic in mind, knowing that teachers could stop participating at any time. The module was constructed using Blackboard Vista (Blackboard, n.d.), the course management and delivery tool provided by one of our universities, and included use of the assessment and email tools as well as discussion forums.
Week 1: Getting to Know You
Week 1 was designed to help teachers and facilitators get to know each other by creating talk and establishing and developing collegial relationships and norms. The engagement began with a Getting to Know You discussion forum, where members could introduce themselves and post comments about each other. Teachers were asked to describe themselves both personally and professionally.
The primary goal of this initial discussion was the development of relationships among participants, with a secondary goal of helping teachers become familiar with Blackboard. We hoped that this type of activity would suffice as an icebreaker and help teachers feel comfortable about posting in later modules. Yet, little opportunity arose for the development of caring as described by Noddings (1984).
Hackenberg (2010), summarizing the work of Noddings, asserted that “caring signals an effort to co-create and participate in social interactions that are responsive to the needs of” those participating (p. 239). In fact, the interactions in this week were superficial and did not lead to teachers becoming engaged in discussions that would help them create a sense of belonging or an environment where they would feel safe to share their thinking about the teaching and learning of mathematics.
In retrospect, two factors missing from the design were pivotal to the development of relationships and teachers’ participation in the balance of the module. First, we made no effort to develop norms of participation with the teachers. In face-to-face interactions, norms for discussions and valuing teacher input can be modeled in words and actions. Such modeling cannot be initiated and sustained the same way in online interactions. Teachers could not see our actions but could only read about them.
This environmental limitation encouraged us to consider providing guidelines and deadlines for participation, an approach colleagues suggested to us. Such an approach was in conflict with our view of constructivist teaching. Instead, we encouraged the teachers to contribute and explore peer contributions by suggesting that they do so. In addition, we modeled such behavior by responding to all the teachers’ posts. Yet, the teachers did not respond to each other’s posts. We missed the opportunity to build norms with the teachers, instead assuming productive discussions would spontaneously emerge.
Second, we struggled to define our role. As interactions between the teachers began, our concern about our actions and contributions grew. We decided not to insert ourselves into their conversation, hoping that teachers would engage, become autonomous, and create a space where it was safe to share. The decision to remove ourselves from conversations was motivated by our value of learner autonomy and concern that the teachers might view our contributions as evaluative. By removing ourselves from the discussions, teachers could neither teach us about their thinking nor learn from our insights.
Fear that the teachers would feel judged or intimidated by our comments overrode our desire to be learners in an emergent community. In constructivist teaching environments interaction fosters the development of relationships and enables teachers and learners to capitalize on learning opportunities. By not questioning and working to connect the teachers, we must have appeared distant and unconcerned about the teachers and their discussions.
Week 2: Task Analysis
Week 2 was designed to initiate teachers’ exploration of proportional reasoning. Teachers were first asked to examine tasks (see Figure 1) and explore whether or not they thought each task had the potential to elicit evidence of proportional reasoning. We chose tasks that pressed teachers to think about essential features of proportional reasoning. Each task was also discussed in forums. Teachers were then asked to generate a definition of proportional reasoning and reflect on the similarities and differences they saw between their own definition and those of other teachers. They were further asked to reconsider their own definition in light of what they noticed. Later, in Week 4, teachers were asked to revisit their definitions. The final activity in Week 2 asked each teacher to identify three of the tasks they were interested in using with their students.
Turkey Problem According to a recipe book, a turkey takes 15 minutes per lb to cook. How long should we cook a 24 lb turkey? | Cherry Syrup Luis mixed 6 ounces of cherry syrup with 53 ounces of water to make a cherry-flavored drink, Martin mixed 5 ounces of the same cherry syrup with 42 ounces of water. Who made the drink with the stronger cherry flavor? (Brown & Clark, 2006) | Pizza Problem Three doctors share one pizza and seven athletes share three pizzas. Who gets more pizza, the athletes or the doctors? (Lamon, 1994) |
Work Problem A crew of 8 people can build a concrete wall in 6 days. If four more people join the group from the beginning, how many days will it take to build the same wall? | Track Problem Sue and Julie are running equally fast around a track. Sue started first. When she had run 9 laps, Julie had run 3 laps. When Julie completed 15 laps, how many laps had Sue run? (Lamon, 1994) | Penny Jar A jar contains 95 pennies and each day Lydia removes 4 pennies from the jar. When will there be zero pennies in the jar? (TERC, 2007) |
Santa Problem Bart is a publicity painter. In the last few days, he had to paint Christmas decorations on several store windows. Yesterday, he made a drawing of a 56 cm high Father Christmas on the door of a bakery. He needed 6 ml of paint. Now he is asked to make an enlarged version of the same drawing on a supermarket window. This copy should be 168 cm high. Approximately how much paint will Bart need to do this? (Van Dooren, De Bock, Hessels, Janssens, & Verschaffel, 2003, p. 205) | ||
| Figure 1. Tasks to provoke questions about proportional reasoning. | ||
During Week 2, we strove to gain insight into the teachers’ mathematics, but also to honor their ways of operating with mathematics problems. The tasks in Figure 1 had consistently provoked productive discussions in face-to-face interactions with teachers. Some teachers would be hesitant to share their mathematical thinking with an unfamiliar group of colleagues, but encouragement typically reduced teachers’ hesitation.
In the AO environment, we did not yet have mechanisms to encourage teachers to do the problems. Teachers in face-to-face interactions typically read the problems but did not solve them. As facilitators, we encourage the teachers to discuss the problems, which often prompts them to solve the problems. With this behavior in mind, we asked teachers to revisit each problem and provide a rationale for their judgments. One goal of the discussion forums for each problem was to provoke disequilibrium as teachers reviewed the reasoning of their peers. Our intent was to encourage teachers to feel comfortable representing their ideas about proportional reasoning to colleagues.
Week 2 was structured to encourage the teachers to compare their initial analysis and discussion with the definitions of proportional reasoning they created. We wanted to gain insight into teachers’ mathematics and how they used it to analyze tasks. The instructional activities for the AO environment were informed by the approaches teachers in our face-to-face professional development sessions had used as they sorted or assessed tasks. In particular, we had typically pressed them to solve or do the tasks before evaluating the potential to elicit proportional reasoning. In the AO environment, we sought to limit demands on how teachers approached the tasks. We reasoned that teachers in the AO environment could act with autonomy, electing to do tasks only as the discussion encouraged them to question their initial evaluation of the potential of a task. As teachers began to see rationales provided by peers and read the definitions crafted, we hoped they would experience disequilibrium regarding their view of proportional reasoning and tasks that might provide it. We anticipated that they might ask each other questions in an effort to address the disequilibrium the tasks and peers’ statements might provoke.
The problems, rationales, and initial definitions of proportional reasoning acted as questions to the community. Teachers began to discuss different rationales and definitions but also asked for guidance in doing some of the tasks. These questions seemed not to encourage the teachers to consider peers’ ideas alongside their own but, instead, encouraged some to share correct answers.
In retrospect, the challenge of the tasks and resulting mathematical answers seemed to dampen some teachers’ participation. We had not anticipated that discussions of the mathematics of the tasks might leave some teachers perhaps feeling dominated by others rather than empowered to share their insights.
Week 3: Children’s Mathematics
Week 3 focused on exploring a problem that teachers typically did not see as provoking proportional reasoning (see Figure 2). Teachers were asked to discuss whether the problem would have the potential to elicit proportional reasoning.
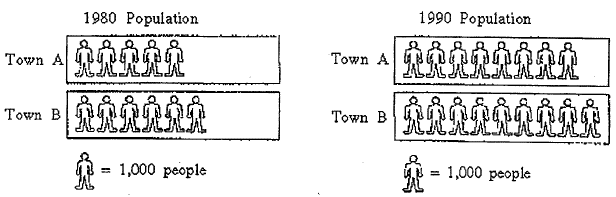 |
| In 1980, the populations of Town A and Town B were 5,000 and 6,000 respectively. The 1990 populations of Town A and Town B were 8,000 and 9,000 respectively. Brian claims that from 1980 to 1990 the populations of the two towns grew by the same amount. Darlene claims that from 1980 to 1990 the population of town A had grown more. |
| Figure 2. Population Problem (Brown & Clark, 2006). |
They then listened to an audio file of a child explaining her solution to the problem. Access to the child’s written work was also provided. Teachers were asked to comment on the child’s reasoning. Fifteen student work samples from the population problem were posted, and teachers were asked to select three work samples and comment on the reasons they found the work interesting.
To develop means to honor the work of teachers and teaching we again turned to what we knew, our experiences with teachers exploring student work in face-to-face professional development. Teachers work quickly and efficiently in classrooms to make sense of children’s work to inform their instructional decision-making. Part of that work is listening to children. The decision to use the population problem was motivated by our reading of the teachers’ initial definitions and analysis of the tasks in Figure 1. The teachers’ uncertainty about what types of problems might have the power to elicit proportional reasoning encouraged us to select a problem that did not resemble the missing value problems teachers often associate with proportional reasoning. The population problem and students’ approaches to the problem in Figure 2 seemed to have the power to provoke further insights about tasks and proportional reasoning.
We conjectured that doubts about proportional reasoning could encourage the teachers to listen differently to a learner’s explanation, perhaps searching for ideas about how the problem might be used to gain insight into a learner’s reasoning. In addition, the experience of hearing a learner’s explanation and exploring the learner’s work might trigger a further elaboration of proportional reasoning.
The audio provided was a child’s rich and elaborate description of her thinking and reasoning to solve the population problem. Throughout the audiotaped session she provided details and the rationale behind many elements found in her written work. Hearing the child’s reasoning seemed to provide an opportunity for the teachers to move beyond evaluating the work samples of other students as correct or incorrect.
The use of the audio was an attempt to challenge teachers’ understandings of proportional reasoning by providing an example that included additive and multiplicative reasoning. Student responses to this problem had the potential to encourage teachers to reflect on children’s development from reasoning that was exclusively additive to reasoning that considered both additive and multiplicative relationships between quantities. The student audio contained strong evidence of additive reasoning and subtle evidence of the emergence of multiplicative reasoning.
Student work samples contained many different explanations. Some of the samples contained incorrect answers based on reasoning identified as additive. Others contained evidence that students might be considering multiplicative reasoning. Finally, there were samples that contained evidence that the student was able to decide whether additive or multiplicative reasoning was applied in the problem.
The goal was to build opportunities to consider the development of multiplicative reasoning as an element of proportional reasoning. Exploration of the student work samples was our question to the teachers, yet unlike the questions in Week 2, this exploration resulted in individual inquiry rather than in collaborative exploration.
In retrospect, the prospect of examining 15 student work samples might have been overwhelming, resulting in the teachers posting their individual analysis without exploring the analyses of others. The activity also failed to encourage the teachers to synthesize their ideas, an instructional activity that might have encouraged peer dialog.
We assumed that hearing a child’s explanation would be more powerful for the teachers and more closely aligned with their interactions with children than the examination of student work samples. Exploring work samples is often done only to assess performance rather than to gain insight into student reasoning that forms the basis for instruction. We anticipated that hearing the child would trigger different emotions and responses from the teachers. In general, we assumed that we knew about the work of teaching and could anticipate the effect of the activity on the teachers.
These assumptions took us further from our usual practice in face-to-face settings. Reading the teachers’ discussions, we were unable to listen with empathy. Evidence of the teachers’ reasoning was visible, yet the AO environment did not allow us to demonstrate our stance as constructivist listeners. Encouraging the teachers to explore ideas was a practice we had not yet developed within the AO environment. We missed a way to demonstrate or convey empathy and silent encouragement that Weissglass (1990) described as a critical component of constructivist listening. A reconstruction of our ideas about constructivist listening or the identification of alternative technology for the AO environment became necessary to allow us to recapture and retool this important element of our practice.
Week 4: Exploring Students’ Work
Week 4 included an activity we had never attempted in our face-to-face professional development sessions. Teachers gathered students’ work samples using one of the tasks from week 2. Our face-to-face professional development sessions were typically too brief to allow for this sort of activity. The timing of the AO professional development seemed perfect for the collection of insights from the teachers regarding their own students’ proportional reasoning. Since the teachers would be ending their school year during Week 4, we reasoned that they might have more flexibility in curricular constraints imposed by schools/districts. The activity capitalized on the authentic work of teaching by allowing the teachers to engage with their own students and discuss that engagement.
Participating teachers were assigned a problem (see Figure 1) based on preferences expressed in week 2 and our understanding of each teacher’s proportional reasoning. They were asked to post 7 to 10 pieces of student work that were representative of their student responses. Two pieces of student work that were most intriguing to them were to be discussed more extensively. After looking across the student work samples, the teachers were asked to describe what they had learned about proportional reasoning and to share questions about proportional reasoning the samples raised.
The relationships that teachers had with their students would provide context and background for their analysis of student work. Finally, teachers revisited their ideas about proportional reasoning and updated their definition. Our hope was that the student work would be yet another strategy to help teachers reconsider their thinking, refine it, and add complexity and depth to their understanding of proportional reasoning.
Once again we experienced dissonance in considering our actions from Week 4 as constructivist teachers. The activity focused on individual teacher exploration and did not result in collaborations among teachers. Yet, we had felt the authentic work of teaching might stimulate discussion. Consideration for the time commitment and the contexts in which the teachers worked might have revealed that there would be little discussion during this busy week of the school year. In fact, while teachers did engage with students and post student work samples, these postings did not provoke questions or discussion from peers.
Our silence and misunderstanding of the activity of teaching suggested our understandings of the demands and constraints on teacher time and motivations for discussion needed further exploration. In retrospect, during the final week of the module the teachers must have felt quite solitary in the AO environment. The mere posts of peers were unlikely to provoke further insight into the proportional reasoning for teaching.
The Complexity of Designing AO Environments
We began our efforts to design an AO professional development environment without careful consideration of the significant differences between AO environments and face-to-face environments. Successful experiences in professional development with activities designed to build proportional reasoning for teaching, the pro-AO climates at our universities, and a desire to move beyond our local professional development contexts encouraged us to begin considering how to conduct professional development online. Prior to designing the AO module, we thought little about what made our professional development experiences in face-to-face environments so successful. The activities and tasks seemed to be the important tools contributing to our success. We failed to consider the significance of the ways we conveyed evidence of listening and caring.
Our conversations about the AO environment unearthed new issues. In face-to-face environments teachers were always asked to share ideas and their reasoning. Opportunities for such sharing were motivated through our encouragement. Yet, as we consulted our university colleagues and other resources regarding how to build AO environments, advice focused on having teachers introduce themselves and setting up rules for when to post and read others’ posts.
We immediately felt uncomfortable with such suggestions, feeling that rules for interaction or guidelines for participation violated teachers’ autonomy. In addition, without knowledge of the teacher’s lives and schedules, guidelines created by the facilitator would likely enable the participation of some teachers and inhibit that of others. We took seriously teachers’ willingness to volunteer to help us learn about proportional reasoning for teaching and did not want to minimize the importance of their autonomy. Yet, our only attempt to build an understanding of the teachers and their contexts was in the Week 1 Getting to Know You activity. In Weeks 2 and 3 we made assumptions about approaches the teachers might take and their access to technology without careful consideration of their needs as learners, the contexts in which they worked, and the demands of those contexts, such as testing schedules or district initiatives.
Discussion
Literature focused on the development of relationships between researchers and teachers highlights the significance of roles and relationships in the encouragement of critical dialog (Goos, 2008; Goos & Geiger, 2008). For example Goos (2008) posed questions regarding who has the “right to ‘transform’ teachers and teaching practices” and “how researchers working with teachers can balance transformation with critique in intellectually honest ways” (p. 232). The development of these questions drew from Goos’ consideration of relationships she had developed with teachers. Key were the ways in which professional developers and teachers supported each other in unfamiliar roles and contexts. This information suggested that our development of the context, in our case the AO environment, without including the teachers and codeveloping views of their roles, likely impacted the ways the teachers engaged in the environment. This understanding is consistent with our motivation for constructivist listening in our teaching.
The development of caring relations (Hackenberg, 2010; Noddings, 1984) seemed significant even as we interacted with the teachers. This factor is primary in the construction of productive, supportive AO environments for teacher professional development. Sztajn (2008), in her discussion of developing caring relationships, suggested gaining insight into the uniqueness of each individual, valuing the unique perspectives of each teacher, and using these in the development of the design of the environment.
We provided an opportunity for the sharing of lived events in our AO environment, but these were meant to be introductions rather than a lever for developing a collaborative, caring relationship. In fact, Week 2 content was available to teachers at the same time as the content from Week 1, in hindsight minimizing the importance of Week 1. The details shared by the teachers were unique elements of the teachers referred to by Stzajn (2008). To convey listening, we might have encouraged teachers to join together in ways that capitalized on their unique characteristics. For example, two teachers were new to the profession. They could have been paired and asked about their experiences. Attending to such details would provide evidence that we wanted to see, hear, and understand the teachers as unique individuals living in contexts unfamiliar, but intriguing to us.
Our ability to create constructivist listening online is a critical element of constructivist teacher practice in AO environments. Yet, many questions emerged regarding how to show evidence of our listening. How could we demonstrate that we were listening and attending to the teachers? How could we show empathy or even interest? In the Blackboard Vista environment, text was the only way to communicate feelings or attention. How might teachers signal to us, or others, that they were sharing ideas and thoughts?
Responses to discussion posts might be shared any hour in any of the 7 days for the module week. In fact, in visiting the module over a year later, there were new posts from the teachers who had not had time to finish the module but were committed to completing the activities even months later. The technology could not notify community members that there was something, or more importantly, someone to consider. Instead, posts containing ideas appeared to be launched into space. Like international pen pals from years ago, talkers were left waiting and wondering if they had been heard at all.
Key tools in AO environments would include methods for notifying community members that a posting has been made. Quick responses to teachers would afford us with opportunities to show we hear and value teacher contributions. Such action has the power to transform informal relationships into caring relations described by Sztajn (2008).
Beyond demonstrating and capitalizing on uniqueness and valuing contributions, our design made assumptions about teachers’ use of technology. We assumed the audio posted during Week 3 would significantly impact teachers’ ideas about proportional reasoning and children’s thinking. Yet, could the teachers open or hear the audio? We had not asked about their access to or familiarity with computer environments. In face-to-face professional development we would want to be sure teachers could see and hear each other or any audio or video used. Indeed, we typically tested to see if this was the case before asking teachers to work with such tools. Often teachers with technology expertise will see our vulnerabilities with technology and help us. Our willingness to be helped shows them that we need them and are willing to be cared for, a critical step in the development of a caring relationship (Sztajn, 2008).
Coupled with our dilemmas about enacting constructivist listening and developing caring relationships, concerns about the technological environment and the technological tools available emerged. While faculty members are being asked by university administrators to develop learning environments using platforms like Blackboard and Moodle, these platforms were developed as course management systems, not as learning community systems. These tools have significant limits that can be overcome only by an MTE’s consideration of learning, interaction, the potential of existing technology, and their creativity with interactions and activities. Such considerations are often beyond the scope of a single MTEs’ existing knowledge and require communities of colleagues to create solutions.
Conversations between all stakeholders in these situations must occur. It is vital that instructional designer, instructional technology specialists, technology developers, and course content experts (instructors) have conversations about what elements of technology would be most useful. Such conversations might focus on elements of practice or factors in practice that encourage productive communities. While, inevitably, MTEs begin with their existing view of practice and how such practices are or are not possible online, reforming practice involves learning with new tools, learners, and environments. Universities must build teams of stakeholders to create productive AO learning environments rather than assuming that MTEs can engage in this work as part of their typical teaching load.
Our experiences with an AO learning environment taught us that our presence cannot be virtual, but must be felt by all of the learners. Selecting not to interact with the teachers likely left them feeling abandoned rather than cared for, perhaps leading to a decline in participation in discussions. We do not know if our participation in voluntary online discussions will dampen the discussions, but we are committed to developing ways of participating in AO environment that illustrate our care for the learners. As we considered qualities we used in our face-to-face practice, tone of voice was considered. We came to view the tone of our voices and those of the teachers as a tool used to convey meaning. Audio and video captures seem to afford MTEs with opportunities to recover tone and its power to shape intended meanings of words.
As Clay, Silverman, and Fischer (2012) have demonstrated in their work, MTEs can develop AO environments that enable teachers to represent their thinking in new ways and use this thinking to develop new understandings. We have come to understand our struggles in designing and interacting in the AO environment as opportunities to develop as teachers. In doing so, we have identified essential elements of our constructivist teaching practice, such as caring relations and listening, that help us build communities with teachers. It remains for us to use this knowledge in collaboration with colleagues in instructional technology to build AO environments and practices that satisfy our need to learn with and from teachers.
References
Anderson, T., & Elloumi, F. (Eds.). (2004). Theory and practice of online learning. Athabasca, Canada: Athabasca University.
Arbaugh, F., & Taylor, M. (2008). Inquiring into mathematics teacher education. In F. Arbaugh & M. Taylor (Eds.), Inquiry into mathematics teacher education (Vol. 5, pp. 1-10). San Diego, CA: Association of Mathematics Teacher Educators.
Berry, A. (2007). Reconceptualizing teacher educator knowledge as tensions: Exploring the tension between valuing and reconstructing experience. Studying Teacher Education, 3, 117-134.
Blackboard. (n.d.). Our story. Retrieved from http://www.blackboard.com/About-Bb/Our-Story.aspx
Brown, C., & Clark, L. (Eds.). (2006). Learning from NAEP: Professional development materials for teachers of mathematics. Reston, VA: National Council of Teachers of Mathematics.
Cameron, A., Dolk, M., Fosnot, C., & Hersch, S. (2005). Turkey investigations, grades 3-5 (Resource Package). Portsmouth, NH: Hienemann.
Clay, E., Silverman, J., & Fischer, D. (2012). Unpacking online asynchronous collaboration in mathematics teacher education. ZDM Mathematics Education, 44, 761-773.
Confrey, J. (1991). Learning to listen: A student’s understanding of powers of ten. In E. von Glasersfeld (Ed.), Radical constructivism in mathematics education (pp. 111-138). Dordrecht, Netherlands: Kluwer Academic Publishers.
D’Ambrosio, B. (2004). Preparing teachers to teach mathematics within a constructivist framework: The importance of listening to children. In T. Watanabe & D. Thompson (Eds.), The work of mathematics teacher educators: Exchanging ideas for effective practice (Vol. 1, pp. 135-150). San Diego, CA: Association of Mathematics Teacher Educators.
Davis, B. (1997). Listening for differences: An evolving conception of mathematics teaching. Journal for Research in Mathematics Education, 1997, 355-376.
Dole, S., Clarke, D., Wright, T., Hilton, G., & Roche, A. (2008). Eliciting growth in teachers’ proportional reasoning: Measuring the impact of a professional development program. In M. Goos, R. Brown, & K. Makar (Eds.), Navigating currents and charting directions: 31st Annual Conference of the Mathematics Education Research Group of Australasia (pp. 163-169). Sydney, Australia: MERGA Inc.
Duffy, T. M., & Jonassen, D. H. (1991). Constructivism: New implications for instructional technology. Educational Technology, 31(5), 7-12.
Even, R. (2008). Facing the challenge of educating educators to work with practising mathematics teachers. In T. Wood & B. Jaworksi (Eds.), The mathematics teacher educator as a developing professional (Vol. 4, pp. 57-73). Rotterdam, Netherlands: Sense Publishers.
Goos, M. (2008). Researcher-teacher relationships in mathematics education. In M. Goos, R. Brown & K. Maker (Eds.), Proceedings of the 31st annual conference of the Mathematics Education Group of Australasia (pp. 227-233). Sydney, Australia: MERGA.
Goos, M., & Geiger, V. (2008). In search of practical wisdom: A conversation between researcher and teacher. For the Learning of Mathematics, 26(2), 33-35.
Hackenberg, A. J. (2010). Mathematical caring relations in action. Journal for Research in Mathematics Education, 41, 236-273.
Jacobs, V., Lamb, L., & Philipp, R. (2010). Professional noticing of children’s mathematical thinking. Journal for Research in Mathematics Education, 41, 169-202.
Jonassen, D. (1998). Designing constructivist learning environments. In C. M. Reigeluth (Ed.), Instructional theories and models. Mahwah, NJ: Erlbaum.
Lamon, S. (1994). Ratio and proportion: Cognitive foundations in unitizing and norming. In G. Harel & J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 89-120). Albany, NY: SUNY Press.
Lee, H., & Mewborn, D. (2009). Mathematics teacher educators engaging in scholarly practices and inquiry. In D. Mewborn & H. Lee (Eds.), Scholarly practices and inquiry in the preparation of mathematics teachers (pp. 1-6). San Diego, CA: Association of Mathematics Teacher Educators.
Lobato, J., & Ellis, A. (2010). Developing essential understanding of ratios, proportions and proportional reasoning. Reston, VA: National Council of Teachers of Mathematics.
Lobato, J., Orrill, C., Bruken, B., & Jacobson, E. (2011). Middle school teachers’ knowledge of proportional reasoning for teaching. Paper presented at the American Educational Research Association, New Orleans, LA. Retrieved from http://www.kaputcenter.umassd.edu/downloads/products/workshops/AERA2011/Lobato_Orrill_Druken_Erikson_AERA_2011.pdf
Lowes, S., Lin, P., & Wang, Y. (2007). Studying the effectiveness of the discussion forum in online professional development courses. Journal of Interactive Online Learning, 6, 181-210.
Noddings, N. (1984). Caring, a feminine approach to ethics and moral education. Berkeley, CA: University of California Press.
Sanchez, M. (2011). Dialogue among in-service teachers in an internet-based mathematics education program. In N. Bednarz, D. Fiorentini & R. Huang (Eds.), International approaches to professional development for mathematics teachers (pp. 98-107). Ottawa, ON: University of Ottawa Press.
Silverman, J. (2011). Supporting the development of mathematical knowledge for teaching through online asynchronous collaboration. Journal of Computers in Mathematics and Science Teaching, 30(1), 61-78.
Silverman, J. (2012). Exploring the relationship between teachers prominence in online collaboration and the development of mathematical content knowledge for teaching. Journal of Technology and Teacher Education 20, 47-69.
Steffe, L. (1990). On the knowledge of mathematics teachers. In R. B. Davis, C. Maher & N. Noddings (Eds.), Journal for Mathematics Education Monograph 4: Constructivist views on the teaching and learning of mathematics (pp. 167-184). Reston, VA: National Council of Teachers of Mathematics.
Steffe, L., & D’Ambrosio, B. (1995). Toward a working model of constructivist teaching: A reaction to Simon. Journal for Research in Mathematics Education, 26, 146-159.
Sztajn, P. (2008). Caring relations in the education of practising mathematics teachers. In B. Jaworski & T. Wood (Eds.), The mathematics teacher educator as a developing professional (pp. 299-313). Rotterdam, Netherlands: Sense Publishers.
TERC. (2007). Investigations in number, data, and space. Parsippany, NJ: Pearson.
Thurston, W. (1994). On proof and progress in mathematics. Bulletin of the American Mathematical Society, 30, 161-177.
Tzur, R. (2001). Becoming a mathematics teacher educator: Conceptualizing the terrain through self-reflective analysis. Journal of Mathematics Teacher Education, 4, 259-283.
Van Dooren, W., De Bock, D., Hessels, A., Janssens, D., & Verschaffel, L. (2003). Students’ overreliance on linearity: An effect of school-like word problems? Paper presented at the the 29th Conference of the International Group for the Psychology of Mathematics Education, Melbourne, Australia.
Vergnaud, G. (1994). Multiplicative conceptual field: What and why? In G. Harel & J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 41-59). Albany, NY: SUNY Press.
von Glasersfeld, E. (1995). Radical constructivism: A way of knowing and seeing. Washington, DC: Falmer Press.
Watson, J., Callingham, R., & Donne, J. (2008). Proportional reasoning: Student knowledge and teachers’ pedagogical content knowledge. In M. Goos, R. Brown & K. Makar (Eds.), Navigating currents and charting directions:31st Annual Conference of the Mathematics Education Research Group of Australasia (pp. 563-571) Sydney, Australia: MERGA Inc.
Weissglass, J. (1990). Constructivist listening for empowerment and change. The Educational Forum, 54, 351-370.
Wilson, P. H., Mojica, G., & Confrey, J. (2013). Learning trajectories in teacher education: Supporting teachers’ understandings of students’ mathematical thinking. The Journal of Mathematical Behavior, 32, 103-121.
Author Notes
Signe Kastberg
Purdue University
Email: [email protected]
Kathleen Lynch-Davis
Appalachian State University
Email: [email protected]
Beatriz D’Ambrosio
Miami University
Email: [email protected]
![]()