A prior version of this paper received the 2012 NTLI Fellowship Award from the Association for Mathematics Teacher Education.
Because of the increasing availability of dynamic statistical software tools, many mathematics teacher educators are beginning to use these tools in courses and professional development for practicing and prospective mathematics teachers. However, to take advantage of these tools for students’ learning, teachers must develop a deep understanding of how to use these tools to explore statistical ideas (Lee & Hollebrands, 2008a, 2011). In this paper, we examine how prospective teachers used representations of data (e.g., tables, graphs, statistical measures) when solving statistical tasks using one of two dynamic statistical software tools: Fathom (v.2.0, Finzer, 2002) or TinkerPlots (v. 1.0, Konold & Miller, 2005).
Features of Dynamic Statistical Software Tools
The fundamental structure of the dynamic TinkerPlots and Fathom environments is such that representations of data are linked as they are created. To create a graphical representation or a summary table, one drags an attribute (variable) name from the data card or data table and drops it onto an axis in a graph window or a row or column in a summary table. This action of dragging an attribute name from the data card or table onto a plot window or summary table is a primary building tool that creates the representation and establishes the internal link between the graph and summary table to the data that is stored in the data card and table.
In Fathom, dragging an attribute onto an axis in a graph window generates a default dot plot of a quantitative attribute and a default bar graph for a qualitative attribute. Within TinkerPlots, however, rather than instantly generating a common graphical display of data, users must actively construct their own representations using the primitive actions of separating, stacking, and ordering. Both programs include built-in connections among all representations created from a data set. Thus, highlighting a case in one representation creates a highlighted display of that case within all other representations.
Both environments provide capabilities to overlay a graph with statistical measures (e.g., mean, median, and a least squares line) and to augment a graph. An augmentation can be made to an existing representation and can provide additional information for analysis. Augmentations are used to (a) alter the representation (e.g., filtering data–in a graph or a table– to show only a specific subset of cases), (b) superimpose something other than a statistical measure in the representation (e.g., moveable line, reference line, show squares, add percentages in bins), or (c) enhance the representation by adding additional information (e.g., color to a plot by selecting another variable that was not initially part of question or a residual plot to show a graph of residuals from a moveable line or regression line already added to the scatterplot).
Video 1 illustrates how to create graphical representations, statistical measures, and graphical augmentations in TinkerPlots 1.0. Video 2 illustrates these capabilities in Fathom 2.0. Both videos also demonstrate how to create dynamic links among representations.
Video 1. Working with representations in TinkerPlots |
Video 2. Working with representations in Fathom |
Overall, the major affordances of dynamic statistical software are the abilities to link representations dynamically and to view different representations, statistical measures, and graphical augmentations simultaneously. Taking advantage of these affordances allows a user to engage in goal-directed activities that may lead to further investigations or additional insights. In this study we were particularly interested in how teachers take advantage of these affordances in their statistical problem solving.
Teachers’ Use of Dynamic Statistical Software Tools
Over the past decade, several researchers have studied teachers’ use of dynamic statistical tools, usually focused within a single professional development experience or course at a specific university (Doerr & Jacob, 2011; Hammerman & Rubin, 2004; Makar & Confrey, 2008; Meletiou-Mavrotheris, Paparistodemou, & Stylianou, 2009). Overall, these studies revealed that dynamic tools can provide opportunities for teachers to improve their approaches to statistical problem solving, moving beyond traditional computational-based techniques and utilizing more graphical-based analysis.
Makar and Confrey (2008) noted that some prospective teachers seemed to use representations in Fathom to investigate a data set in ways that allowed them to develop hypotheses and use data to explore and make a claim (6 of 18) and to explore variables systematically in a data set leading them to an interesting claim (8 of 18). Doerr and Jacob (2011) reported that the choices in representational capabilities in Fathom allowed teachers to illustrate their understanding of sampling distributions. In addition, they found significant improvements in teachers’ overall statistical reasoning and in their understanding of graphical representations.
In studies involving TinkerPlots and Fathom, teachers often combined graphical and statistical measures by either adding a measure to a graph or using a graph to make sense of a statistical measure computed separately. Such analyses by teachers often afford opportunities to consider an aggregate view of a distribution that incorporates reasoning about centers and spreads (Konold & Higgins, 2003). For example, the in-service teachers in the study by Meletiou-Mavrotheris et al. (2009) used graphical representations in TinkerPlots to notice the impact of a particularly high or low value in a distribution and to examine the impact on a measure of center if this apparent outlier was removed from the data set. Although a focus on an interesting point may indicate a focus on data as individual points, the teachers also demonstrated use of graphs to describe patterns in a distribution and group propensities.
A focus on group propensities was also noted by others as well. Hammerman and Rubin (2004) analyzed how teachers tended to use the capability of binning data in TinkerPlots (segmenting a distribution range into several parts to group data visually within a range). Middle grades teachers in McClain’s (2003) study used minitools with some characteristics and tools similar to those available in TinkerPlots 1.0. McClain found that an early way that teachers explored their data was to use cut-points to examine percentages in subregions of a distribution. These teachers then used these percentages to support their claims about how data was partitioned and to attend to the relative density across distributions being compared.
Although prior research has discussed how teachers represent and analyze data where a link among representations may often be inferred, this research often has not focused explicitly on how, why, and to what extent teachers utilized linked representations. We are interested in the representations of data that teachers create and what they do once the links, which are internal to the technology environment, are established. Do teachers take advantage of the additional linking affordances to examine and analyze their data intentionally? We focus on the intentionality of this action because it indicates a decision to take advantage of the dynamic nature of the tools to explore data in specific ways for making claims and decisions.
Users may take advantage of two different ways to link: dynamic and static. A dynamic link occurs when a purposeful action is done to one representation that causes a reactive and coordinated action in another representation. Often these actions result in a visible highlighting of individual cases across representations (e.g., selecting one case in a graph and seeing that case highlighted in a data table or flipped to in the data cards or selecting a range of cases in one graph and seeing those same cases highlighted in a separate graph window). At other times these actions primarily change one representation by adding a layer of additional information (e.g., dragging an attribute name to the middle of a plot window in Fathom adds color or changes an icon shape; clicking on an attribute name in the data card in TinkerPlots recolors the cases in the plot window based on the gradient or color scheme assigned to that attribute).
A static link within a dynamic technology environment occurs when there is evidence of coordinating complementary information in two or more representations (Ainsworth, 1999) that does not require any direct technological interaction with a representation. When viewing a dot plot of an attribute and a separate box plot of the same attribute, a teacher or student may coordinate the information in each plot. They may notice that while the lower whisker has a large range, almost all the data is stacked near the lower end with a significant gap in the distribution, as seen in the dot plot. If this coordinating and noticing was done without technological actions, then a static link was used.
Our specific research question was as follows: When reporting their statistical problem solving with dynamic statistical software, in what ways do these reports indicate prospective teachers’ use of representations, including dynamic and static links, during their problem solving?
Conceptual Framework
The ways teachers use dynamic statistical software to solve statistical tasks can provide insight into their understandings about both statistics and how to utilize the power of technology in doing statistics. Lee and Hollebrands (2008a, 2011) proposed a framework that characterizes the important aspects of knowledge needed to teach statistics with technology (see Figure 1). In this framework, three components consisting of statistical knowledge (SK), technological statistical knowledge (TSK), and technological pedagogical statistical knowledge (TPSK) are envisioned as layered circles with the inner most layer representing TPSK, a subset of SK and TSK. Thus, Lee and Hollebrands proposed that teachers’ TPSK is founded on and developed with their TSK and SK. The research reported in this paper examines only components of teachers’ SK and TSK. Statistical knowledge encompasses the following characteristics:
- Engaging in statistical thinking
- Recognizing need for data
- Transnumerating
- Considering variation
- Reasoning with statistical models
- Integrating the context
Technological statistical knowledge encompasses
- Automation of calculations and representations
- Emphasis on data exploration
- Visualization of abstract concepts
- Simulations
- Investigations of real data
- Collaborative tools
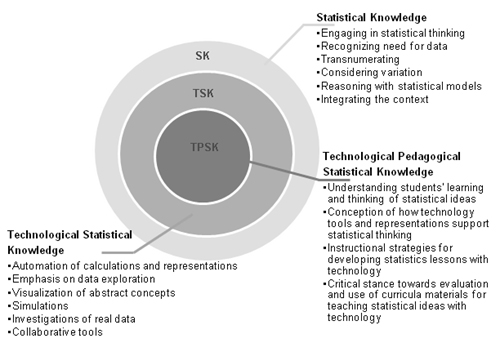 |
| Figure 1. Components of technological pedagogical statistical knowledge. (Adapted from Lee & Hollebrands, 2011). |
Within SK we are interested in prospective teachers’ abilities to engage in transnumeration (Wild & Pfannkuch, 1999) as a process of transforming a representation between a real system (real-world phenomena) and a statistical system (ways of modeling the phenomena statistically) with an intention of engendering understanding (Pfannkuch & Wild, 2004). Thus, teachers should be able to engage in a statistical problem solving cycle to collect data, represent the data meaningfully with graphs and compute appropriate statistical measures, and translate their understandings of the data back to the context. Transnumeration can afford new insights into data when data is represented in a way that highlights a certain aspect related to the context of data.
Within TSK, our focus was on how prospective teachers take advantage of technology’s capabilities to automate calculations of measures and generate graphical displays and the ways they use these graphs and measures to explore data and visualize abstract ideas (Chance, Ben-Zvi, Garfield, & Medina, 2007). Thus, we considered how prospective teachers used technology to visualize data in graphical form, compute and visualize measures (e.g., mean), use graphical augmentations (e.g., shade a region of data or show squares on a least squares line), and take advantage of ways to link multiple representations.
Methods
Many studies conducted with teachers have been from a single site and with a relatively small sample of teachers. In contrast, our research group examined teachers’ use of dynamic statistical technology environments with teachers enrolled in courses from eight different institutions in the United States in which faculty were using the same curriculum materials (Lee, Hollebrands, & Wilson 2010). In these materials, teachers are engaged as learners and doers of statistics through exploratory data analysis. The curriculum includes data from contexts that are likely of interest to teachers (e.g., national school data, vehicle fuel economy, birth data) that can promote the practice of asking questions from data. TinkerPlots and Fathom are used to engage teachers in tasks that are designed to develop their SK and TSK simultaneously. Throughout the materials, findings from research on K-12 students’ understandings of statistical ideas are used to make points, raise issues, and pose questions. In addition, teachers are encouraged to consider pedagogical implications of various uses of technology on students’ understanding of statistical ideas (see Lee & Hollebrands, 2008b, for design of materials).
Data Collection
The results reported here are based on analyses of teachers’ reports of their work on three tasks that involve similar statistical concepts and tools in either TinkerPlots or Fathom (see Table 1). The faculty members implementing the materials attended a 5-day summer institute to become familiar with technologies, specific tasks and data sets, and pedagogical issues. Across institutions, materials were implemented in a variety of courses, some focused on using technology to teach middle or secondary mathematics and others on statistics for elementary or middle school prospective teachers. Because of the variety of goals and objectives in these courses, we expect that the teacher educators adapted the materials in ways to best fit their courses.
The courses predominately enrolled prospective teachers, with a few practicing teachers or graduate students. (Henceforth, for brevity, the participants in this study will be referred to as teachers.) Thus, the mathematical and statistical background of the teachers varied widely, as did their intended grade level focus (K-12).
When completing a task, teachers each worked individually and created a document that described their work, including illustrative screen shots of ways they used technology in solving the task. A total of 247 reports on these three tasks, submitted as a Word document or a TinkerPlots or Fathom file, were collected across institutions and blinded to protect teacher, faculty, and institutional identity. Data on the Chapter 1 task (n = 102) were collected from five institutions and six instructors. Two instructors at two different institutions collected teachers’ work on the Chapter 3 task (n = 41). A total of 104 documents were collected for the Chapter 4 task from six different instructors across four institutions.
Table 1
Research Tasks
| Task as Posed in Materials |
| Ch 1 Task TinkerPlots | [Note: Faculty members had a choice of two similar data sets to use of state level school data from two regions of the US. Data included attributes such as average teacher salary, student per teacher ratios, expenditures per student.] Explore the attributes in this data set and compare the distributions for the South and West [Northeast and Midwest]. Based on the data you have examined, in which region would you prefer to teach and why? Provide a detailed description of your comparisons. Include copies of plots and calculations as necessary.
|
| Ch 3 Task Fathom | Explore several of the attributes in the 2006Vehicle data set. a. Generate a question that involves a comparison of distributions that you would like your future students to investigate. b. Use Fathom to investigate your question. Provide a detailed description of your comparisons and your response to the question posed. Include copies of plots and calculations as necessary.
|
| Ch 4 Task Fathom | Explore several of the attributes in the 2006Vehicle data set. a. Generate a question that involves examining relationships among attributes that you would like your future students to investigate. b. Use Fathom to investigate your question. Provide a detailed description of your work and your response to the question posed in part a. Include copies of plots and calculations as necessary. |
Analysis Procedures
To begin analysis, four documents were randomly selected from each chapter. Through iterative discussions by the research team, including examining documents and making sense of teachers’ work, both top-down methods (Miles & Huberman, 1994) and grounded theory (Strauss & Corbin, 1990) were used to develop and apply a coding instrument. The coding instrument that emerged was based on theory from research on statistical problem solving, particularly, cycles of exploratory data analysis and typical phases (ask a question, represent data, analyze/interpret, and make a decision, e.g., Wild & Pfannkuch, 1999); use of static and dynamic representations in statistics and other domains of mathematics; and categories and codes that emerged from analyzing an initial random sample of teachers’ work.
In the coding procedures, each teacher’s work was chunked into smaller cycles of investigation that included four phases. Within each phase, several categories were used to characterize the work.
Phase 1. Choose Focus
- Question
- Informing focus
- Attributes used
Phase 2. Represent and Explore Data
- Representations created
- Measures
- Augmentations
- Coordination among representations, dynamic or static
Phase 3. Analyze and Interpret Data
- What is noticed
- Interpretation with context
- Interpretation without context
Phase 4. Make Decision
- Make a claim
- Continue investigation
Figure 2 illustrates our coding structure. The phases “Represent and Explore Data” and “Analyze and Interpret Data” often happened simultaneously as teachers reported their exploratory data analysis. However, with the particular focus in our research question on the ways in which teachers used representations, we applied codes within the two separate phases. See the appendix for a sample of teachers’ work that has been annotated to illustrate the four phases of a cycle of investigation and how various codes were applied.
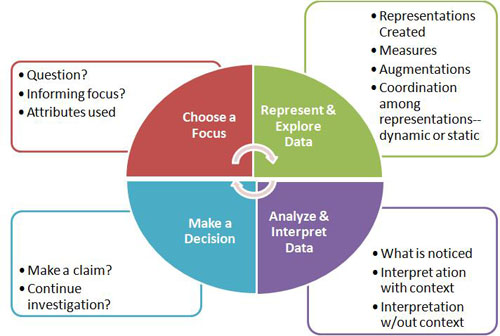 |
| Figure 2. Problem solving phases and coding categories used in analysis. |
Sampling Documents for Detailed Analysis
Often in qualitative research, the quantity of documents to review can be overwhelming. This was the case in our collection of 247 documents. In addition, from an initial review of all documents, it was obvious that some responses were more detailed than others, contained more statistical investigation cycles, and used more representations. Thus, each document was reviewed and classified as either short or long. Short responses were typically one page in length and included one or two screen shots with minimal explanation; others were classified as long responses. In the second phase of analysis, a stratified random sample was chosen to have proportional representation of short and long responses from each collection of chapter responses and to represent about 25% of our documents overall (see Table 2).
Table 2
Design of Stratified Random Sample
Total Documents Collected | Stratified Random Sample | |
| Chapter 1 | ||
| Short | 52 | 13 |
| Long | 50 | 12 |
| Total | 102 | 25 |
| Chapter 3 | ||
| Short | 12 | 4 |
| Long | 29 | 8 |
| Total | 41 | 12 |
| Chapter 4 | ||
| Short | 38 | 9 |
| Long | 66 | 16 |
| Total | 104 | 25 |
All documents in the stratified random sample from Chapter 1 were submitted in Microsoft Word, in which text was interspersed with illustrative screen shots. Of the randomly selected documents 7 of the 12 examined from Chapter 3 and 6 of the 25 examined from Chapter 4 were submitted as Fathom files; the remaining were Word documents. Within a Fathom file, teachers could leave representations viewable and write their responses in text boxes.
Eight researchers were paired in seven coding dyads (six researchers served in two dyads). Each dyad was randomly assigned 8 to 12 documents to code. All documents were initially coded individually, and then the pair met to discuss, compare, record interrater reliability, and come to consensus for each document.
Each teacher’s report of the problem-solving process was segmented into different cycles of investigation, where each cycle consisted of some work in each of the four phases depicted in Figure 2. The critical shift from one cycle to the next was whether teachers seemed to be making a claim, expressing the need to “dig deeper,” or were abandoning their current focus and choosing a new one (often choosing a new attribute of interest or tweaking the focus of a question to allow for a finer-grained examination).
Sometimes the use of a dynamic link was explicit in teachers’ reports because they had a screenshot with two or more representations highlighted or they reported that they clicked one case in one representation and saw it highlighted in another representation. At other times, however, the use of dynamic linking was implicit. The coders inferred implicit dynamic linking based on their knowledge of software capabilities as well as what was reported in the teachers’ documents (for an example, see the appendix).
When coding pairs met, they recorded interrater reliability (IRR) on many categories. The overall IRR for several coding categories used in this paper, across all documents, was 0.746 for number of cycles, 0.923 for types of representations used, and 0.940 for measures added to representations. There was low initial agreement about coding an augmentation to a graph (0.523), which led to discussions to establish a better definition of a graphical augmentation and reclassification of all documents based on this definition. After the IRR was recorded, pairs of coders would discuss disagreements until a final consensus was reached. On a few occasions, the opinion of a third independent coder was used to help reach consensus.
After the qualitative coding was complete, each document was given one summary code for several new categories. For example, we created a new category to describe how many unique types of representations a teacher used, as well as a total number of representations used in the report. These summary codes became a condensed data set for further analysis. We were able to create descriptive statistics for several categories, as well as conduct informal comparisons across several categories and use formal statistical techniques to examine differences among some categories with an alpha set at 0.05. Findings from the qualitative and statistical analysis of the condensed summary codes for the 62 cases inform the results that follow.
Results
Recall that the documents submitted by teachers were their own reports of their problem solving and conclusions to the tasks posed (Table 1). Thus, we note that our analyses and interpretations were limited to the processes and representations the teachers chose to report.
Characterizing Teachers’ Statistical Problem Solving
To begin our characterization of teachers’ problem solving, we focused on the number of cycles of investigation and whether teachers answered the initial question, either the one posed in the task (Chapter 1), or the question(s) they posed for themselves (chapters 3 and 4). In 55% of the 62 analyzed documents, teachers utilized one or two cycles of investigation, while 24% utilized three to four cycles. The distribution of the number of cycles was skewed to the right, as 11% utilized five to six cycles and 8% utilized seven to eight cycles. One teacher in Chapter 4 used 13 cycles, a clear outlier. Sixty percent of teachers who completed the Chapter 4 task utilized one to two cycles, 58% in Chapter 3, and 48% in Chapter 1.
Although most of the documents initially classified as being “short” used one to two cycles (77%), several were coded as having three to six cycles (23%). Likewise, several teachers’ reports initially classified as “long” also indicated they engaged in only one to two cycles of investigation (39%), but they had written more in their report about what they did and showed multiple screenshots of representations they had created. The large percentage of teachers who used only one to two cycles seems to be related to their decision to focus on a single attribute in Chapter 1 (typically average teachers’ salary) or to pose a question in Chapter 3 or 4 that would not require several cycles of exploratory data analysis.
There was high variability, from three to eight, in the distribution of cycles across each chapter. When three to four cycles appeared in Chapter 1 documents, it was often because a teacher had chosen a few attributes of interest, possibly from a hypothesis that a particular attribute would be most influential in their analysis and decision as to which region they should teach. For example, one teacher chose a focus on “average salary, number of students per teacher, and the number of teachers…because…they are important indicators of employment opportunities and working conditions.” Teachers with a higher number of cycles (five to seven) in Chapter 1 tended to explore most or all quantitative attributes in the data set.
In Chapter 3, a few teachers explored several sets of variables and posed different questions for each, rather than working only on one main question. In Chapter 4, a few teachers with a higher number of cycles seemed to be engaged in a more open-ended exploration of relationships among several attributes. The data were unclear as to whether they were trying to focus on one particular relationship to learn something specific.
Teachers’ focus in their problem solving is likely guided by the type of question they are solving. To study further the nature of the questions these teachers explored and the number of reported exploratory cycles, we examined two additional codes in the multivariable data set from the Choose a Focus phase for Question Type and Number of Attributes. For Question Type we used two categories (adapted from Arnold, 2009) to indicate if the question teachers were answering was “broad” (had elements in the question that would require a more open problem-solving process and perhaps more exploratory data analysis) or “precise” (was focused on a specific goal or hypothesis, which could involve simple or complex analysis).
Because all teachers were responding to the same posed broad question in Chapter 1 (see Table 1), their question type was labeled broad, regardless of whether they decided to narrow the focus through their work. In the Chapter 3 and Chapter 4 tasks, teachers were asked to pose one or more of their own questions; thus, each of their questions was coded as either broad or precise.
Overall, 60% of teachers were working on answering a broad question and 40% on a precise question. Considering only questions posed by teachers in chapters 3 and 4, 32% were broad, while 62% were precise. Teachers working on broad questions, across all chapters, used significantly more attributes from the data set (p = 0.00096) and had a higher mean number of cycles (p = 0.031).
Almost all teachers answered the initial question they had set forth to investigate. Eight of the 62 teachers, some from each chapter task, did not clearly make a final claim or definitive statement about the question they were investigating. These data do not seem related to the type of question they were answering; of the 8 who did not answer their question, 4 were responding to precise questions and 4 were responding to broad questions.
Characterizing Teachers’ Work Representing and Exploring Data
To organize the analysis of how teachers reported their use of representations, we discuss the four major coding categories within the “Represent and Explore Data” phase in our cycles of statistical investigation (see Figure 2). Our analyses include trends across all 62 cases, as well as disaggregated trends by chapter.
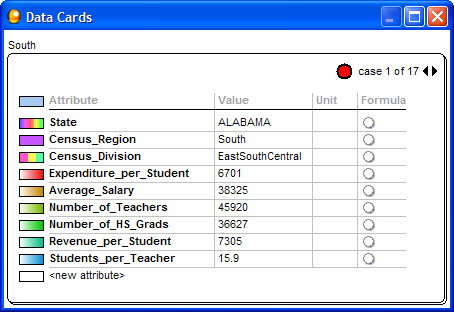
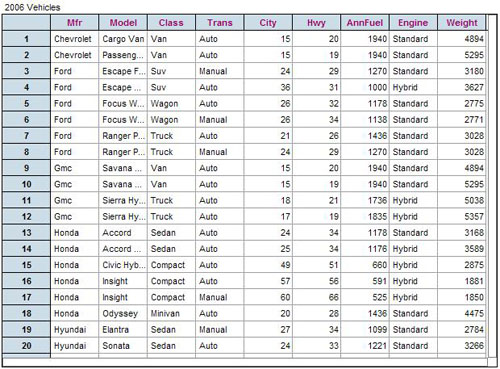
Representation Creation. In coding Chapter 1 documents, we did not specifically list a data card of a collection as a representation of that data, as it was automatically available in the TinkerPlots file for this task. Data Cards (see Figure 3) look like a stack of index cards, with each card representing a case (e.g., the state of Alabama) and containing the values for that case for each attribute (e.g., average salary, census region) in the data set. We did consider the Data Card, however, as a representation that could be linked to other representations. The Fathom file containing the data used for the Chapter 3 and 4 tasks opened with data already shown in a Data Table (see Figure 3). Thus, as with the Data Cards in TinkerPlots, the Data Table in Fathom was not specifically listed as a representation created by teachers; however, if a teacher used the table when linking to another representation such as a graph or summary table, it was considered a linked representation.
|
|
| Figure 3. The Data Cards representation in TinkerPlots and Data Table in Fathom. |
There was high variability in the number of representations created across all chapters, with most teachers using between one and six representations (82%), as evidenced by the number of screenshots included in their reports or the number of representations visible in their Fathom files. However, teachers’ reports from Chapter 1 mostly included one unique type of representation (18 of 25), with the remaining seven cases using two unique types of representations. In chapters 3 and 4, teachers much more commonly used between three and five unique types of representations, 67% and 32% respectively.
One outlier used seven different types of representations in Chapter 4. In chapters 3 and 4, many teachers used a summary table, 75% and 36%, respectively. A summary table is a representation (available in Fathom but not in TinkerPlots) that can be used to generate specific statistical measures. Thus, even though Chapter 1 text materials introduced teachers to using five different representations, they tended to use only one type.
Of the teachers working on Chapter 3 and Chapter 4 tasks, seven used a high number of representations (from 8 to 18). Four of these teachers had submitted their work in a Fathom file; the one clear outlier in the group who used 18 representations did so in a Word document. Thus, although it seems likely that using Fathom as an analysis and reporting environment may give better insight into all the representations teachers created and used, the data do not point directly to such a trend. We suspect that when reporting work in a separate document that includes screenshots of their work, teachers may not report all of the representations they used.
Overall, the teachers chose to use appropriate graphical representations for the questions they were answering. In the case of chapters 1 and 3, with questions focused on comparing distributions, by far the most common representations were double box plots (50 occurrences in Chapter 1 by 18 teachers and 25 occurrences in Chapter 3 by 7 teachers) and double dot plots (10 in Chapter 1 by 5 teachers and 12 in Chapter 3 by 6 teachers). For Chapter 4, these two representations were included, respectively, six times by 5 teachers and nine by 5 teachers. A few other representations included summary tables (19 in Chapter 3 and 20 in Chapter 4), scatterplots (three in Chapter 3 and 39 in Chapter 4), histograms (two in Chapter 3 and 14 in Chapter 4), and binned plots (12 in Chapter 1).
The overabundance of double box plots and double dot plots can be attributed to the fact that 37 teachers explored a comparing-distributions task and appropriately chose a representation that would facilitate comparisons. However, this overabundance can also be suggestive of what teachers have learned to do within the software and those representations with which they are most comfortable. Many Chapter 4 reports used histograms, a representation that was not emphasized in the Chapter 4 text materials, though histograms were used in both chapters 1 and 3.
Use of Measures. In general, teachers used appropriate measures related to the question they were pursuing. The most commonly used measures in Chapter 1 were mean and median; in Chapter 3 they were count, mean, median, and five number summary; and in Chapter 4 they were least square lines and corresponding equations.
In addition to identifying the most common measures used, we considered whether teachers computed these measures by superimposing them on a graph or by adding them to a summary table. Many teachers used summary tables in Fathom to compute various statistics. In Chapter 3, a summary table was found 19 times in nine documents. In Chapter 4, the summary table was present 20 times in nine documents. Fifty-eight percent of teachers added statistical measures to graphical representations in Chapter 3 and 56% added them in Chapter 4, as compared to 72% of the teachers in Chapter 1. However, two teachers were clear outliers, as they produced multiple graphical representations and added multiple measures to each graph in Chapter 3.
While one teacher appeared to be marking common measures in a normal distribution (mean, mean+stdev, mean-stdev), another seemed mainly to be using a graph window as a place to compute a statistical measure (e.g., IQR, StDev) whose location in the distribution did not add a way to reason about the measure in relationship to the aggregate. Most of the teachers who added measures to a graph did so in TinkerPlots, which can be attributed to features of TinkerPlots and Fathom. Whereas, Fathom offers the ability to summarize statistical measures in a summary table, TinkerPlots affords easily incorporating summary statistics, such as measures of center, on graphical representations with the click of an icon on the graphing toolbar. (Note: Plotting a value that is a statistical measure on a graph in Fathom is possible, but requires a more complex procedure.)
Use of Augmentations. Teachers working on chapters 1 and 4 tended to use some form of augmentation in their representations, 19 (72%) and 11 (44%), respectively, out of 25. Teachers’ work on the Chapter 3 task showed less evidence of the use of augmentations (4 out of 12, or 33%). Augmentations were most commonly used as superimposed over a current graphical representation. The most common of these augmentations for Chapter 1 included showing and hiding outliers, adding a reference line, inserting dividers to shade a region, and ordering the data. In Chapter 4, the most common superimposed augmentations were adding moveable lines and showing squares.
Augmentations that enhance a graph with additional information were also present in teachers’ reports from all chapters. In Chapter 1, several teachers added counts and percentages for a specific region of data and added color to the graph by selecting an attribute in the data card. In Chapter 3, two teachers added color or icons to a graph. Five Chapter 4 reports enhanced a graphical representation by adding color to a graph by selecting a new attribute; 4 teachers also added a residual plot to a scatterplot. In most cases, these augmentations seemed to support teachers’ claims about group propensities, either about the entire distribution, or about a subpart or region of data. Augmentations that altered the representation were the least common; 2 teachers in Chapter 3 and 4 teachers in Chapter 4 added a filter to show only a specific subset of the data. Again, this augmentation was used to support examining group or subgroup trends.
Linking Among Representations. Whether and how a teacher took advantage of the dynamic linking capability in the software was of particular interest to us as a way of capturing how much a teacher interacted with data across multiple representations. About 43% of the documents across all chapters did not indicate that teachers engaged in linking representations. Forty percent of teachers’ work clearly indicated the use of dynamic linking, while about one fourth of the sample responses demonstrated the use of static linking (Table 3). Chapter 1 teachers seemed to use dynamic linking the most (52%), while only 2 of 12 showed evidence of dynamic linking in Chapter 3. Fifty percent of teachers showed evidence of static linking in Chapter 3.
Table 3
Number of Teachers Providing Evidence of Linking Representations
No Evidence of Linking | Dynamic Linking | Static Linking | |
| Chapter 1 (TinkerPlots) n = 25 [a] | 11 (44%) | 13 (52%) | 3 (12%) |
| Chapter 3 (Fathom) n = 12 | 5 (41.67%) | 2 (16.67%) | 6 (50%) |
| Chapter 4 (Fathom) n = 25 [a] | 11 (44%) | 10 (40%) | 6 (24%) |
| Totals (n = 62) [a] | 27 (43.5%) | 25 (40.3%) | 15 (24.2%) |
| [a] Percents do not sum to 100 since two cases in Chapter 1 and two cases in Chapter 4 were coded as both static and dynamic. | |||
In chapters 1 and 3, the most common use of dynamic linking was to coordinate a single graph with either a data card or data table to find out details about a specific case of interest. Only occasionally, in solving the Chapter 1 and Chapter 3 tasks, did teachers use dynamic linking to look at an interval of data (see Figure 4). However, teachers who linked representations in a dynamic way in Chapter 4 often were comparing the position of groups of cases across graphical representations and using such noticing to make statements about relationships (see Figure 5). Static linking was done in all chapter tasks to compare trends in graphs of different attributes within and across cycles. Teachers often made static links toward the end of their problem solving, as they reflected on their work across cycles and made a final decision.
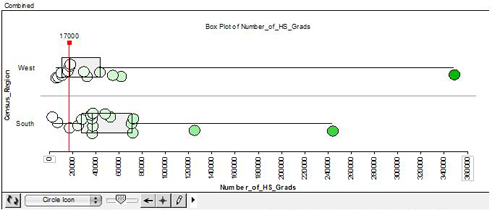 |
| The next attribute I looked at was the number of high school grads. First of all the median for the West only has 17,000 high school grads where the South has about 37,000 grads. This is a big difference, and I think that it basically tells me that the South has more students. Also, the West has 1 outlier, California, and the South has 2 outliers, Florida and Texas. I would not take this into consideration when choosing a place to teach because the data would have to be percentage of high school grads for it to mean anything. This is just because there are more students in the South. |
Figure 4. Example of one teacher using dynamic linking to identify state names of data points considered outliers. |
| I chose to use a histogram because it is easier to select a set of points and see where it is lies [sic] in the corresponding graph. It organizes it a little better and is clearer to read and understand. I then proceeded to select certain values given in the City graph and compared it to the AnnFuel graph. |
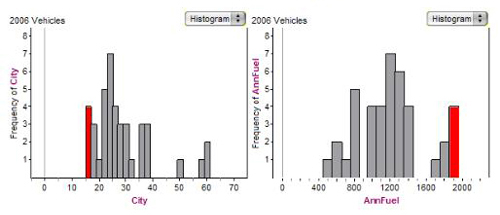 |
| I continued this process selecting every bar in the City graph and looking at its values in the AnnFuel graph. The only time these values were not completely opposite were in the middle and a few areas they split between two sections. For examples, see below… |
| Figure 5. Example of one teacher using dynamic linking in Fathom to examine a relationship in two attributes. |
Connections Among Statistical Problem Solving and Representing and Exploring Data
Although teachers working on Chapter 1 most often used one graph per investigation cycle, teachers working in chapters 3 and 4 typically used more than one graph per cycle. A much wider variety of graphical representations (simple box plots and dot plots, double box plots and dot plots, histograms, scatterplots) were used in Chapter 4 in responding to questions about relationships among attributes, and almost always there was more than one representation per cycle.
The type of question a teacher investigated was related to the types of representations that were used and how they explored data with those representations. Teachers who were answering broad questions used significantly more types of augmentations (p = 0.00063) and added more statistical measures to graphs (p = 0.032); however, there was no significant difference between type of question explored and number of representations used or number of unique types of representations used. Thus, if given an opportunity to engage in problem solving around a broad question, perhaps teachers will be more apt to take advantage of the software capabilities to augment graphs and add statistical measures to graphs. This action may lead to an enhanced understanding of how these features of the software can aid in their own and future students’ exploratory data analysis.
In considering the ways teachers may have used their TSK, we further examined relationships among their actions of augmenting graphs, adding statistical measures to graphs, and linking representations. Teachers who dynamically linked representations tended also to augment a graph (84% across all chapters) and add statistical measures to graphs (72%). Most of the teachers who either did not link representations or only statically linked representations also tended not to augment a graph (76%); approximately 43% of this group did not add any statistical measures to graphs. In fact, teachers whose reports indicated that dynamic linking occurred used more graphical augmentations than did those teachers who did not dynamically link (p = 0.013).
No significant difference existed between these two groups as to their frequency of adding statistical measures to graphs. These results seem to suggest that teachers who engage in dynamic linking may also interact more with the graphical representations by adding statistical measures and augmenting the graphs. Those who do not dynamically link also add statistical measures to their graphs, but seldom utilize graphical augmentation tools in their work.
When linking two graphs, a level of analysis happened after a user had linked the two graphs (clicking on one region in a histogram and seeing the same cases highlighted in another histogram). In these situations, the students must view the linked data, make sense of it, and draw conclusions about its meaning. In contrast, if they link a single case in a graph to a table or data card (eight in TinkerPlots and two in Fathom from Chapter 3) to find out which was the special case, little to no additional statistical meaning-making is required after the linking action.
In Fathom, teachers tended to link representations to examine group propensities. The task of looking for relationships may have facilitated this type of linking and focus on group propensities. Although the linking in comparing distribution tasks in chapters 1 and 3 did not appear to assist teachers in the analysis of group propensities, it was a vehicle for moving between an aggregate view of data to an individual view. Researchers have claimed that tasks involving the comparison of distributions can help teachers and students to view data as an aggregate and can improve their ability to discuss group propensities (e.g., Konold & Higgins, 2003; Konold & Pollatsek, 2002; McClain, 2003, 2008). Our findings support these claims. In addition, our findings suggest that teachers’ use of augmentation tools and superimposing statistical measures on graphs, more so than using linking capabilities within the software environments, can support this move toward examining group propensities. Thus, if a goal of students’ learning in statistics is to be able to make claims about group propensities and to view distributions as an aggregate, then mathematics teacher educators should pay particular attention to assisting teachers in developing their abilities to use augmenting tools and the capability to overlay statistical measures in a graph in dynamic statistical software.
Discussion
Given the dynamic nature of Fathom and TinkerPlots and the emphasis placed on using dynamically linked representations in the curriculum materials used in this study, it was somewhat surprising to discover that only slightly more than half of teachers’ responses provided evidence of either dynamic or static linking among representations. Lack of evidence of linking does not mean that teachers did not engage in this activity. Maybe, they simply did not provide detailed information in their reports that could be used to infer that linking had occurred. In addition, those who linked in the Chapter 1 and Chapter 3 tasks apparently did so for similar purposes, often focused on examining a specific individual case, whereas the teachers who linked in Chapter 4 often did so to examine group propensities. This difference is likely related to the nature of the tasks (comparing distributions versus finding relationships among attributes).
Most of these prospective teachers had little experience in using the dynamic statistical technologies and in reporting details of their statistical problem solving before being exposed to the Lee et al. (2010) materials. In addition, the teacher educators were in their first year of implementing this new textbook. As early learners of these tools, most of the teachers represented and explored data in ways similar to the approaches that were taught in the materials. However, it is revealing to learn which of the techniques they chose to use and which techniques they used that were different from those presented in the textbook. We wonder about the benefits and drawbacks of writing a report in a Word document versus within a dynamic statistical environment. Using Fathom as an analysis and reporting environment may give better insight into all the representations teachers created and used. When reporting work in a separate Word document, teachers may not report all the processes or representations used. However, having to transfer screenshots and create a report in Word may require teachers to engage in an additional level of processing, so that they make decisions about the most important aspects to present. Comparing teachers’ Fathom or TinkerPlots files with their redacted Word documents could lend insight into teachers’ ability to engage in this level of synthesis.
Our cross-institutional results add to the prior research done at smaller scales that have illustrated the powerful ways teachers can use graphical representations and augmentations on those representations to make meaningful claims based on data (e.g., Hammerman & Rubin, 2004; Makar & Confrey, 2008; McClain, 2003, 2008;). Specifically, we recommend that mathematics teacher educators provide teachers with many opportunities to engage in tasks posed with broad questions using multivariable data sets that explicitly encourage multiple representations of data and use of dynamic linking, augmentations, and statistical measures.
Teachers need opportunities not only to compare distributions, but also to examine relationships among variables. These opportunities should be paired with discussions that make explicit how certain representations and use of augmentations and linking can assist (teachers as well as their future students) in making sense of data. Such an approach may facilitate teachers’ understanding and use of the dynamic affordances in their statistical work, thus assisting in the development of their SK and TSK. Teachers with a deeper knowledge base in SK and TSK can plan lessons and engage students in meaningful statistical problem solving with powerful dynamic statistical software in ways that can likewise increase students’ SK and TSK.
References
Ainsworth, S. E. (1999). A functional taxonomy of multiple representations. Computers & Education, 33, 131-152.
Arnold, P. (2009, July). Context and its role in posing investigative questions. Paper presented at the sixth annual conference of the International Collaboration for Research on Statistical Reasoning Thinking and Literacy, Brisbane, Australia.
Chance, B., Ben-Zvi, D., Garfield, J., & Medina, E. (2007). The role of technology in improving student learning of statistics. Technology Innovations in Statistics Education, 1(1). Retrieved from http://escholarship.org/uc/item/8sd2t4rr
Doerr, H., & Jacob, B. (2011). Investigating secondary teachers’ statistical understandings. In M. Pytlak, T. Rowland, & E. Swoboda (Eds.), Proceedings of the Seventh Congress of the European Society for Research in Mathematics Education (pp. 776-786). Retrieved from http://www.cerme7.univ.rzeszow.pl/WG/5/CERME_Doerr-Jacob.pdf
Finzer, W. (2002). Fathom dynamic data software (version 2.1) [Computer software]. Emeryville, CA: Key Curriculum Press.
Hammerman, J. K., & Rubin, A. (2004). Strategies for managing statistical complexity with new software tools. Statistics Education Research Journal, 3(2), 17-39.
Konold, C., & Higgins, T. (2003). Reasoning about data. In J. Kilpatrick, W. G. Martin, & D. Schifter (Eds.), A research companion to principles and standards for school mathematics (pp. 196-215). Reston, VA: National Council of Teachers of Mathematics.
Konold, C., & Miller, C. D. (2005). TinkerPlots: Dynamic data exploration [Computer software]. Emeryville, CA: Key Curriculum Press.
Konold, C., & Pollatsek, A. (2002), Data analysis as the search for signals in noisy processes. Journal for Research in Mathematics Education, 33, 259-289.
Lee, H. S., & Hollebrands, K. F. (2008a). Preparing to teach data analysis and probability with technology. In C. Batanero, G. Burrill, C. Reading, & A. Rossman (Eds.). Joint ICMI/IASE study: Statistics education in school mathematics: Challenges for teaching and teacher education. Proceeding of the ICMI Study 18 and 2008 Roundtable Conference, Monterrey, MX. Retrieved from http://www.ugr.es/~icmi/iase_study/Files/Topic3/T3P4_Lee.pdf
Lee, H. S., & Hollebrands, K. F. (2008b). Preparing to teach mathematics with technology: An integrated approach to developing technological pedagogical content knowledge. Contemporary Issues in Technology and Teacher Education, 8(4). Retrieved from https://citejournal.org/vol8/iss4/mathematics/article1.cfm
Lee, H. S., & Hollebrands, K. F. (2011). Characterizing and developing teachers’ knowledge for teaching statistics. In C. Batanero, G. Burrill, C. Reading, & A. Rossman (Eds.), Teaching statistics in school mathematics – Challenges for teaching and teacher education: A joint ICMI/IASE study (pp. 359-369). New York, NY: Springer.
Lee, H. S., Hollebrands, K. F., & Wilson, P. H. (2010). Preparing to teach mathematics with technology: An integrated approach to data analysis and probability. Dubuque, IA: Kendall Hunt Publishers.
Makar, K., & Confrey, J. (2008) Dynamic statistical software: How are learners using it to conduct data-based investigations? In Batanero, C., Burrill, G., Reading, C., & Rossman, A. (Eds). Joint ICMI/IASE Study: Teaching statistics in school mathematics: Challenges for teaching and teacher education. Proceeding of the ICMI Study 18 and 2008 Roundtable Conference, Monterrey, MX. Retrieved from http://www.ugr.es/~icmi/iase_study/Makar_ICMI17.pdf
McClain, K. (2003, July). Supporting teacher change: A case from statistics. Paper presented at the 27th International Group for the Psychology of Mathematics Education Conference. Retrieved from ERIC database (ED501024).
McClain, K. (2008). The evolution of teachers’ understanding of distribution. In Batanero, C., Burrill, G., Reading, C., & Rossman, A. (Eds). Joint ICMI/IASE Study: Teaching statistics in school mathematics: Challenges for teaching and teacher education. Proceedings of the ICMI Study 18 and 2008 Roundtable Conference, Monterrey, MX. Retrieved from http://www.stat.auckland.ac.nz/~iase/publications/rt08/T2P8_McClain.pdf
Meletiou-Mavrotheris, M., Paparistodemou, E., & Stylianou, D. (2009). Enhancing statistics instruction in elementary schools: Integrating technology in professional development. The Montana Mathematics Enthusiast, 6(1 & 2), 57-78.
Miles, M. B., & Huberman, A. M. (1994). Qualitative data analysis: An expanded sourcebook. Thousand Oaks, CA: SAGE Publications.
Pfannkuch, M., & Wild, C. (2004). Towards an understanding of statistical thinking. In D. Ben-Zvi & J. Garfield (Eds.), The challenge of developing statistical literacy, reasoning, and thinking (pp. 79-95). Dordrecht, The Netherlands: Kluwer Academic Publishers.
Strauss, A., & Corbin, J. (1990). Basic of qualitative research: Grounded theory procedures and techniques. Thousand Oaks, CA: SAGE Publications.
Wild, C., & Pfannkuch, M. (1999). Statistical thinking in empirical enquiry (with discussion). International Statistical Review, 67, 223-265.
Author Notes
The research reported here is partially supported by the National Science Foundation (DUE 08-17253). The opinions expressed herein are those of the authors and not the foundation. Information about the project can be viewed at http://ptmt.fi.ncsu.edu.
Thank you to the following individuals for their valuable work as part of the research team: Dusty Jones, Robin Angotti, Kwaku Adu-Gyamfi, Karen Hollebrands, Marggie Gonzalez, and Tina Starling.
Hollylynne Stohl Lee
North Carolina State University
email: [email protected]
Gladis Kersaint
University of South Florida
email: [email protected]
Suzanne Harper
Miami University
email: [email protected]
Shannon O. Driskell
University of Dayton
email: [email protected]
Keith R. Leatham
Brigham Young University
email: [email protected]
Appendix
Sample Coded Document

![]()