Emergent Public Spaces: Generative Activities on Function Interpolation

Technology forms a powerful tool of ever-increasing value in the arsenal of the contemporary educator. The rapid progress of technological innovation has transformed the mathematics classroom in numerous ways. One way in which this transformation has happened is in the development of tools such as network-based technologies, which allow for the recording and reviewing of conclusions reached through group dynamics. For this reason, preservice teachers, who themselves will don the garb of the instructor in due course, must take the time to familiarize themselves with the creative power unleashed by technologies that can facilitate the implementation of curricular activities focused on student understanding in order to inform their teaching.

In many regards, preservice teachers find themselves in a unique position to experience the benefits of new technologies and activities imported to the classroom (Kersaint, 2007). Teacher educators must ensure that the preservice teachers continually maintain an internal dialog concerning what they are learning and how the technology can be used to extend their experience of learning individually to one of participating in environments that also allow for group-level learning.

Particularly, preservice teachers need exposure not only to new technologies for incorporation in their future classrooms, but also to the new possibilities of classroom interactions and reconceptualizations of mathematical content that the newly created learning environments will allow their future students. Generative activities (Stroup, Ares, & Hurford, 2005) provide a framework for constructing such mathematics learning environments that are also purposefully designed for groups (Stroup, Ares, Hurford, & Lesh, 2007).

In this particular study, we present a case in which a generative activity about interpolation and function approximation is the key element for establishing an environment that allows the development of mathematical understanding in a group. The activity also serves to illustrate the role of network-based technologies in the interaction between learning and instruction and documentation of student learning. In generative activities, diversity of student individual participation generates a space of solutions that is both social and mathematical and that characterizes the learning that emerges from each group (as also in Stroup, Ares, & Hurford, 2005).

As network-based technologies become more widely used in the classroom and researchers conduct studies to better understand the dynamics of student learning through activities designed for groups, teacher preparation programs must provide preservice teachers with these types of learning experiences that most likely did not form part of their previous academic history.

This study presents three groups of students as they worked through a generative activity on interpolation in a calculus context. One group of students formed part of a first-year calculus course directed at majors in the social sciences, natural sciences, and engineering. The other two groups were comprised of preservice teachers taking one of the required science, technology, engineering and mathematics (STEM) education courses to get teacher certification as they simultaneously worked toward their degree program in one of the STEM areas.

In each case, the students employed a network-based environment with graphing calculators, where their work was displayed anonymously on a screen for all to see. This display provided for an immediate and efficient way for students to share their understanding and allowed the instructor real-time assessment of student thinking to guide the classroom discussions.

We wanted to characterize the (personal and public) mathematical space of solutions of each class as a way to describe the mathematical activity of students. The purpose was to determine whether the context of a calculus class would lead to a qualitatively different mathematical space of solutions than the one generated by students who engaged in the same activity in the context of a class on learning theories in STEM education. This comparison would allow us to make inferences about the appropriateness of this generative activity as a blueprint for the mathematics learning environments preservice teachers may need to generate in their future classrooms and about the suitability of this activity in the context of a course on learning theories in STEM education.

Background

Framework

In order to explore and characterize student learning from these groups, we took a hermeneutical stance to better understand the interplay between mathematical and social activity as they take place in the classroom (Skovsmose, 1998). In contrast to an absolute and externally defined notion of mathematics, this perspective views an individual’s experience of the world, actions, and language as a dynamic mathematical and social interaction.

Brown (2002) stated that the system and structure of mathematics “can never be seen in its totality and is always accessed through specific action.” This interpretive perspective on the learning of mathematics requires that students put mathematical expression to their experience and have a way of assessing the appropriateness of the expression in particular situations through an “on-going fitting of language to mathematical activity” (Brown, 2002, p. 69).

Using this framework, Brown described mathematical activity by highlighting the notion of personal space.  In a personal space individuals perceive themselves as acting and manipulating objects that are seen and handled from the world within reach. This space spreads beyond what is within a given individual’s immediate reach to the boundaries defined by the situation and the people with which the subject interacts: “The personal space of any individual also incorporates some concern about other people sharing the social situation and how these people contribute to the perceived constraints.” (p. 136)

As individuals interact within a group situation, their personal spaces overlap and share certain characteristics. We use the term public space to refer to those aspects of an interactive situation shared by the personal spaces of participants. In this environment individuals can build awareness of their personal space for action through learning how the world and others change in response to them.

Generative activities distinguish themselves from other group learning environments reported in the literature (e.g., Clark-Wilson, 2010; Rasmussen & Stephan, 2008) by the (personal and public) space-created play they generate. As described by Ares, Stroup, and Schademan (2009), space-created play arises when individual students are required to provide an expression with a particular mathematical characteristic (e.g., something equivalent to 4x) or to convey a strategy to attain a shared goal (e.g., prevent your agent from obtaining a “disease” in an environment interacting with other peer agents). The collection of students’ individual expressions generates a public space with an emergent mathematical (and social) structure co-constructed by the group. The public space created from students’ individual participation goes beyond the aggregate (e.g., showing students’ individual responses simultaneously), to generating a public space that is not pre-determined. Rather, this public space is a new entity. It is emergent and co-constructed by the group with its own mathematical structure that is distinct from the one in the individual students’ personal spaces. The mathematical space allows for multiple solutions, where student-generated contributions can be varied and yet all be mathematically valid.

In the context of mathematical activity, individuals create mathematics in the physical and social situation they inhabit. The physical world, including physical tools and symbols, provides support in learning by anchoring cognitive processes, rather than fixing conceptions. In their study, Ares et al. (2009) described a generative activity with an elevator participatory simulation using a wireless network of graphing calculators that collected students’ individual input to their calculators, projecting their collective inputs on a screen at the front of the room and displaying the emergent system in real time. The authors viewed the worksheet tasks and calculators as artifacts that provided private space for students to investigate, test, and assess relationships in the mathematical content addressed by the task (velocity, position, motion graphs, etc.).

In their personal space, students interact and are able to decide when and what aspects of their work they want to share in the public space. Thus, the public space helped students to “make their thinking visible” as the new collective system is generated (Ares et al., 2009). The display of the emergent public space becomes a dynamic representation of the individual and collective activity as it evolves. Students’ mathematical statements made during the course of activity are seen as “snapshots along the way and serve to orientate thinking which continues to evolve” (Brown, 2002, p. 98).

Classroom documentation of student understanding, individually and collectively, is important because it provides evidence of what and how they are thinking about relevant mathematical ideas.  This information can be used by the teacher to provide students with pertinent feedback and to make decisions about instructional practices. One of the most effective ways to improve how teachers teach is to help them become familiar with the nature of students’ developing mathematical knowledge (Carpenter, Fennema, Franke, Levi & Empson, 1999; Black & Wiliam, 1998a, 1998b).

Studies are needed that focus on better understanding the relationship between the emergent pedagogies from network-based environments and teacher education. One recent study provides findings that these technologies offer a natural progression toward a collaborative learning environment, which was perceived by teachers as productive for student learning because it continuously fostered formative assessment practices (Clark-Wilson, 2010).

Ares et al. (2009)  made constant reference to the fundamental role of their participating teacher in generating a productive learning environment for individual students and for the group. Teachers who engaged in teaching with these technologies were facilitated by the environment to capture student thinking, which was used to make instructional decisions, promoted meaningful mathematical classroom discourse, and increased opportunities for purposeful student self- and peer assessment (Clark-Wilson, 2010).

In comparison with individual documentation, evidence of student thinking in the group space has been much less explored and researched because of the methodological and technological challenges (Rasmussen & Stephan, 2008).

This study highlighted certain ways in which generative activities may be coupled with network-based technologies in the context of teacher preparation to enhance preservice teachers’ cognizance of how their own experience as students provides a blueprint for the learning environments they may need to generate in their future classroom. This study focused on a limited portion of the personal space—personal space the students chose to share in the public space. The study focused on the evidence of student individual and collective thinking as documented in the generated public space and explored and characterized the generated mathematical space of solutions.

Activity

The present study focused on functional interpolation of points in the context of calculus. The literature already provides numerous examples of how other concepts have been studied, such as functions (Eisenberg, 1991; Janvier, 1987; Kieran, 1997; Malik, 1980; Thompson, 1994; Wagner, 1981), limits and continuity (Davis & Vinner, 1986; Ferrini-Mundy & Graham, 1994; Juter, 2006; Millspaugh, 2006; Núñez, Edwards, & Matos, 1999; Sierpinska, 1987; Tall & Vinner, 1981), derivative (Asiala, Cottrill, Dubinsky, & Schwingendorf, 1997; Aspinwall, Shaw, & Presmeg, 1997; Habre & Abboud, 2006; Ubuz, 2007), and integral (Orton, 1983; Rasslan & Tall, 2002; Thompson & Silverman, 2008).

However, function interpolation provides an example of an important topic that has received relatively short shrift. Its importance stems in part from how it bridges the gap between the classical continuum analysis of calculus and the discrete world of data points encountered in computer technology, in particular, in numerical analysis. Precisely because of its position at the intersection of classical theory and technological applications, interpolation provides a unique opportunity for studying how students interact with technology and the impact of this interaction on learning.

This approach fits with research encountered in previous studies, such as Cantoral and Montiel (2003), who designed an activity intended to improve student understanding of Lagrange interpolation polynomials through a gradual sequence of problems. Although the activity considers the use of handheld graphing calculators, they provided no mention of any attempt to promote opportunities where the students could learn collectively with a shared public space that promotes eliciting and documenting student thinking.

The activity employed in the present study can be characterized by a generative design (Stroup, Ares, & Hurford, 2005; Stroup, Ares, Hurford, & Lesh, 2007). As described elsewhere in this paper, a critical element in these types of activities is a context in which participation of all students is encouraged and each student’s contribution receives a visual representation in the public space. The teacher should foster a continual dialog between students, facilitating individual participation and relating it both to the contributions of others and to the emergent mathematical structure.

More specifically, the present study concentrates on a modeling task that should be meaningful, shareable, and reusable and should elicit students’ mathematical thinking in some visible way.

In many respects, network-based technologies are ideal tools for supporting generative learning environments, embodying personal and public spaces by allowing for individual participation (through the use of handheld graphing calculators or laptops networked to the teacher’s computer acting as a server) that is represented publicly (a projection of the teacher’s computer screen). Student participation is made visible and documented in the public space at the individual and group levels, which serves as a point of reference for students to discuss, refine, and revise their ideas continuously.

This particular activity employed the graphing calculators as participatory tools. In this system, information finds its way from students’ devices to the teacher’s computer and vice versa. Students can, therefore, submit and view their individual responses in the public space displayed from the teacher’s screen, and the teacher can send contributions from the public space to individual students’ devices.

The research question driving our study was as follows: Does the implementation of a generative activity on function interpolation lead to a qualitatively different mathematical space of solutions when used in a calculus class as compared to its use in the context of a class on learning theories in STEM education?

This comparison allowed us to make inferences about the appropriateness of this generative activity as a blueprint for the learning environments preservice teachers may need to generate in their future classrooms and about the suitability of the use of this activity in the context of a course on learning theories in STEM education that is part of the teacher preparation program. For example, the preservice teachers may have generated a less productive mathematical space than the group taking the calculus class. This result could call into question the appropriateness of the use of this generative activity for assisting in the development of learning environments in K-12 classrooms and the pertinence of introducing these types of environments within the context of a course on learning theories in STEM education. In order to analyze possible differences, we characterized the personal and public mathematical space of solutions of each class as a way to describe the mathematical activity of students.

Methods

This research was conducted in three classrooms at a large public university in the southern U. S. One group was derived from a first-semester calculus course for students majoring in the social sciences, natural sciences, or engineering; the remaining two groups consisted of preservice teachers taking one of the courses on learning theories in STEM education that is required in their teacher preparation program. For the purposes of description, we will refer to the general-major, first-year students as Group 1 and to the preservice teachers as Groups 2 and 3.

Group 1 was formed by 79 students who volunteered to participate in this study, out of 110 enrolled in the class. The curriculum for this course covers the first eight chapters of the textbook Calculus (Stewart, 2003), a standard textbook used in first-year calculus courses in numerous universities throughout the country.

Groups 2 and 3 were comprised, respectively, of 6 students (out of 10 enrolled) and 8 students (out of 20 enrolled) who chose to participate in this study. Students enrolled in this teacher preparation program major in one of the STEM areas and are required to take additional courses in the education department specifically designed to prepare students in STEM education in order to obtain certification as secondary school teachers. In particular, their participation in this study took place while they were taking a required course in learning theories in STEM education. Their coursework not only provided these preservice teachers with a strong background in STEM content, but also in the integration of content and pedagogy within STEM.

The activity utilized the Texas Instruments Navigator System (TI-Nav), which provides a wireless network of graphing calculators (TI-84+) connected to the teacher’s computer. The teacher’s computer acted as a server, projecting a display of the public space in which students’ contributions were displayed. Given the limited number of calculators that can be supported in this network, a maximum of 32 calculators was used in Group 1, and six and eight calculators, respectively, were used for Groups 2 and 3. Students in Group 1 were asked to work in pairs to promote discussion and increase participation. A total of 64 students responded via the available TI-84+ calculators connected to the network. The remaining 15 students in the class worked with similar graphing calculators and were asked to register their responses on an activity sheet. This was the first time students from the three groups used the TI-Nav and the particular activity center available for this environment.

The classroom episode was divided into two major sections to be performed in the span of one 50-minute class period. The first section was an activity designed by Stroup (Stroup & Davis, 2004; Stroup, Carmona, & Davis, 2005). It allowed students to accustom themselves to the instructional environment provided by the technology. The second section focused on the intended interpolation activity itself:

1. Activity 1: Playing with the system. In order to familiarize students with the use of the TI-84+ and the TI-Nav system, students were asked to contribute with two points per calculator.  Each student was represented by a different icon (or agent) on a Cartesian plane, which formed the public space displayed by the teacher’s computer.  Students had three connected challenges which were addressed in the following order:
   1. Go to a place on the plane where x is negative and y is positive;
   2.  Mark two points where the value of y is twice the value of x;
   3.  Write an equation of a curve going though all the points contributed by the students.

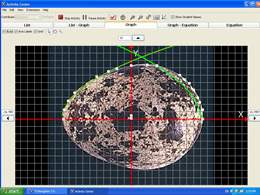
1. Activity 2: The Egg Hunter Activity.  In this activity, students were asked to contribute to the public space to model a real quail egg, with its 2-dimensional cross-section projected on the screen.  This module strove to elicit from students ideas about interpolation, continuity, and the analysis of functions.  Student contributions followed in two stages:

1. Data Generation: Students were asked to place a single point that accurately marked the outer boundary of the top half of the egg.
2.  Modeling: After all the students submitted their points, the instructor transmitted the points to students’ calculators.  Students were then asked individually to find a function that best fit (i.e., contained or touched) all of the points.  Once students submitted their functions, discussion focused on which of the submissions best fit the projected contour of the egg.

To find the volume of the quail’s egg within single-variable calculus, the students would eventually employ the technique of analyzing a solid of revolution.  By this technique, the solid is formed by revolving a single-variable curve f(x) about the x-axis.  The volume is then found by noting that the cross-section perpendicular to the x-axis forms a circular disk whose radius at position x0 is the function value f(x0).  The area of this circular disk, as a function of x0, is therefore

and so the total volume of the solid could be obtained by integrating this area along the x-axis:

To accomplish this ultimate goal, the necessary first step was to find the height f(x) of the outer boundary of the egg as a function of x.

Students in Group 1, who were in only their first semester of calculus, had already been exposed to the necessary techniques of integration, but they had not previously discussed interpolation in class.  Students in Groups 2 and 3 were already required to have completed a minimum of 1 year of their STEM major before enrolling in the teacher certification program.  They were expected to devise their own solutions based on the concepts of functions and continuity with which they were already familiar.

The entire session was recorded on video, with the camera focusing on the projected public space. The data collected for this study consisted of student activity sheets, video, and field notes written by the research team. One of the authors conducted the activity while another made observations and remained available to assist students with the technology.

The analysis focused on characterizing the classroom by the documentation provided in the public space over class time. We conducted a discourse analysis to characterize the social and mathematical structures that emerged from the classroom interactions. Data analysis involved reviewing the videotape multiple times. First, an outline was generated providing a timeline of mathematical activities during the two tasks. Initially, a first overview was described in terms of the instructor’s and students’ roles and identifying different types of interactions: of the instructor with students, with the public space, and with the mathematical ideas emerging over time.

Second, each mathematical expression submitted by students to the public space was recorded, providing the time of submission. From this chronological list we characterized the mathematical structure of the dynamic public space by identifying instances where students or the instructors focused on particular characteristics of the emergent mathematical structure. These instances were identified whether of a single expression submitted by an individual student or from a collection of expressions that generated it. Several screen shots from the public space were captured through the recorded video in order to document particular instances of the evolving public space.

Results

Figure 1 shows a representative image of the points contributed by students to delineate the border of the egg. Figure 2 shows the functions, along with their graphs, that were shared in the public space by students from Group 1. Proposed functions can be characterized in several ways. The characterization emphasized by this class involved the degree of the equation. For example, the most frequent type of equations populating the public space involved quadratics (e.g., Y1 = .05 (X^2) + 7.5; Y1 =  -1/25 (X^2) + 7.28) and radicals (Y1 = [-.43(X^2) + 50]^0.5). Other submissions included trigonometric equations (e.g., Y1 = sin (X) – 10), and a variety of equations demonstrating other mathematical aesthetics; for example, Y1 = X((e^(49)/2) + 7) [sic].

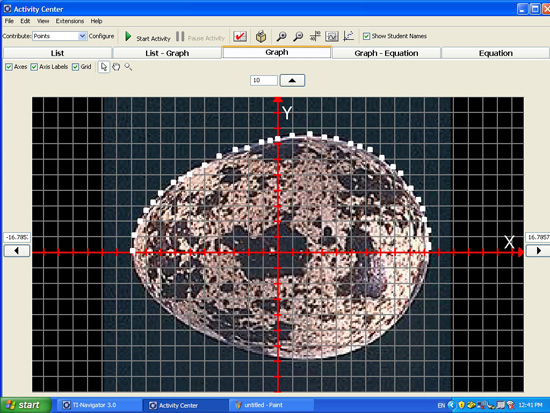
Figure 1. An example of points submitted by students to delineate the upper boundary of the egg.

The public space was populated in batches in relatively little time. The first batch of submissions lasted about 3 minutes before the instructor paused to discuss the emergent mathematical structure that had been generated thus far as documented in the public space. The sequence of students’ equations revealed the dynamic interaction between the personal and public spaces and elicited the mathematical structures that students deem to be better in the context of the activity (e.g., better fit to the curvature of the egg). For example, during the initial 50 seconds, 5 students submitted different equations (each student is provided with a different username—e.g., FFF):

This public space continued to populate rapidly. Although all equations were different, many of the subsequent submissions seemed to follow a pattern from a reinterpretation of some of these initial equations producing a refined version from the previous ones. The collection of these refinements was produced by individual students testing their equations in their personal space.

For some students, the mathematical activity focused on refinement of a mathematical equation previously submitted that was considered a good fit but that could still be improved. Sometimes the source equation had been submitted by another peer; on other occasions, students submitted second and third equations that were refinements of their previous work. As an example of the former, student FFF submitted equation Y1 = -.05 (X^2) + 7 to the public space at time 36:43, then, student HHH submitted Y1 = -.05 (X^2) + 0.1x  + 7.5 to the public space at time 37:42 as a refinement of student FFF’s first submission.  Later, at time 38:10, student RRR did further refined student HHH’s submission by sharing his equation, -.05 (X^2) + 0.1x + 7 in the public space.

The following case illustrates the latter example. At time 38:39, student PPP shared Y1=-.05 (X^2) + 7.5 in the public space, a refinement of student FFF’s first equation. She then refined her first submission and shared her second refinement Y1=-.05 (X^2) + 7.6 at time 39:23. Each of these instances exemplify different types of interaction between students’ personal and public spaces. When shared, the collection of these equations generated an emergent mathematical structure that characterized the public space at that point in time.

When captured at different times, these screen shots provided trails of documentation of the dynamic public space and the evolving mathematical ideas. Students were able to validate their responses, first in their personal space, then in the public space by assessing how well their new equations fit the contour of the egg.

The teacher facilitated the subsequent discussions by asking students which of the submitted equations better met the criteria of best fit to the contour of the egg and explicitly encouraging students to provide comments and suggestions for improving the work of others. The students of Group 1 focused on a more refined collection of functions that they decided best fit the points. One cluster of these functions took the general shape:

.

When prompted by the teacher, students voiced their opinions, supporting their choice for which of the following pairs of parameters (a,b) worked best: (49,-0.45), (50,-0.45), (49,-0.49). Student justification mainly relied on how the curves fit the contour of the egg. The teacher also identified other clusters of students’ equations, which she characterized to the class as quadratics: binomials and trinomials and smaller clusters on trigonometric functions.

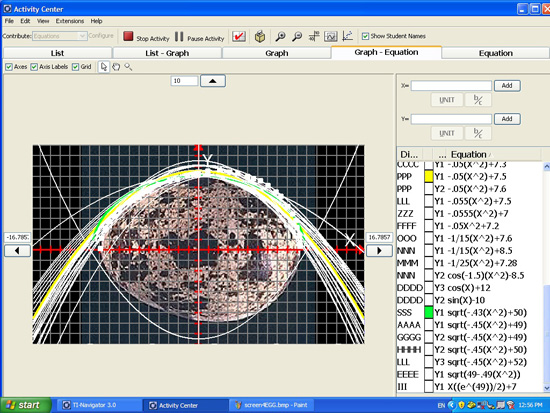
Figure 2. Students’ attempts at finding a function passing through all the points on the egg’s boundary.  Group 1.

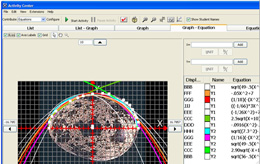
The preservice teachers of Groups 2 and 3 showed a greater range of functional forms despite the fact that the groups consisted of far fewer students. A video screenshot of the generated public space is provided in Figure 3. The greater variety in large part followed from a tendency to use function composition. One striking point of departure from the results obtained with Group 1 was the use in Groups 2 and 3 of piecewise-defined functions.

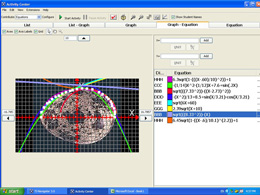
(a) Group 2

(b) Group 3

Figure 3. Student attempts at finding a function passing through all the points on the egg’s boundary.

As can be seen in the screenshot presented in Figure 4, as the teacher focused the discussion, these functions generally took the form:

In these types of functions, students split the domain at the point x = 0, which they identified as a “point where the shape of the curvature of the egg changed.” For example, Figure 4(a) represents the piecewise-defined function:

while Figure 4(b) represents:

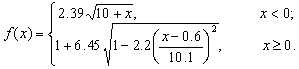
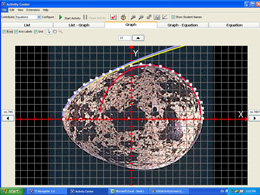
(a) Graph of G(x).

(b) Graph of H(x).

Figure 4. Graphs of fits via piecewise-defined functions.  Group 2.

As with Group 1, the fits encountered by Group 2 contained sections with the form

 ,

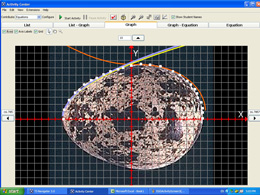
but the piecewise definitions allowed for some departure from this form over that portion of the domain where students decided there was less agreement on where the egg curvature changed. Similarly, the screenshot in Figure 5 depicts two fits proposed by Group 3, which bear a marked structural resemblance to the results of Group 2, via the functions:

and

(a) Graph of G(x).

(b) Graph of H(x).

Figure 5. Graphs of fits via piecewise-defined functions.  Group 3.

Discussion

This study focused on the implementation of a generative activity on function interpolation and analyzed qualitative differences in the mathematical spaces of solutions generated by three groups of students. We explored and characterized each group by their respective generated mathematical space of solutions in order to assess the suitability of the implementation of this learning environment for learning about mathematics and pedagogy in mathematics in the context of a course on learning theories in STEM education and the appropriateness of using this generative design in their future learning environments.

The following discussion focuses on the characterizations of these groups in three identified topics that emerged from our analysis: interactions between a student’s personal and public spaces, characterizations of the groups based on the public space they generated, and technology and documentation of the emergent mathematical ideas.

Personal Space Shared Publicly

Several researchers have reported classroom environments where students were constrained to use the language of others because the constructive use of discourse was undermined (e.g., Filer, 1993; Newmann, 1992). In generative activities, students are not constrained to use the language of others, yet our results show that others’ language can become one common resource that students use. In this context, the practice became cognitively and socially productive. As presented in our results with this generative activity, even when students used the language of others, their discourse provided instances of productive mathematical and social learning interactions.

In instances when some students used the language of others by varying an equation shared into the public space by another peer, it is hard to justify that this recreation of another’s expression was cognitively weak or that was caused by lack of interest. Even in such putative cases, we have evidence that when students used an equation previously submitted in the public space, their decision followed from their assessment that their peer’s expression involved a curve that was good but could be improved, highlighting this expression as an interesting direction to pursue. Evidence of instances when students engaged in this type of activity was provided when they used the equations presented in the public space and changed specific parameters to generate new curves that fit the data better than the previous submissions.

This adaptation involved making a decision regarding which equation to choose, what parts of the equation needed amendment, and which ones should remain intact required from the student an understanding of the mathematical structure of the previously submitted expression and its relationship with the graph representing it. It also required students to predict how modifying the selected parameters would create the new graph that would be a better fit. Beyond communication, this exercise entailed identifying a mathematically productive idea, operating on someone else’s knowledge, and thus, understanding someone else’s knowledge in order to create and recreate equations that make visible these highly complex mathematical and social activities.

The instructor also played a central role in making students’ participation more productive mathematically. When the teacher elicited students’ continual participation, the structure of the activity allowed them to build on the group’s ideas. That is, when the instructor required students to provide comments and suggestions for improving the work of others, students demonstrated they are able visually to identify other peers’ responses and interpret their graph and corresponding equation.

In order to create these refinements by providing a new equation, students showed understanding of how the values from the equation could be improved, as was validated when their  graph fit the data points better than the preceding equation. The cognitive complexity of this task required students to make connections between both types of representations (graphs and algebraic equations) and be able to anticipate how changes in the expression would modify the graph to better fit the curvature of the egg. In addition, students were able to make sense of their own responses in relation to the responses of other students, allowing a better understanding of the mathematical ideas embedded in the generated public space. Their expression has mathematical value with respect to the expression of another and of the group.

Characterization of the Group in the Public Space

Within Group 1, it was clear that students valued the idea of arriving at a function determined by a single equation over the accuracy of a curve that coincided with all the points of the boundary of the egg. Conversations with students during the activity confirmed this perception. Given that the students were taking a course on calculus, they felt compelled to address immediately the mathematical property of continuity of a function: their knowledge of the Fundamental Theorem of Calculus suggested to them that to help ensure that the function could be integrated it should also be continuous. These students believed that the best way to ensure the continuity of a function would be to identify a single expression for the entire domain.

The space generated by Groups 2 and 3 centered more on accuracy: the preservice teachers did not see a disconnect between meeting the condition of continuity and providing piecewise-defined functions that would allow a better fit over the whole domain. In addition, students from both preservice teacher groups expressed a holistic perspective on curvature, viewing part of their task as trying to fit accurately the overall boundary of the egg. In contrast, the first-semester calculus students in Group 1 viewed curves they submitted as best fits because “they go through all the points.”

Technology and Documentation of Emergent Mathematical Ideas

The graphing calculators admit an ease of graphing heretofore difficult to come by. They allow students to redraw an entire curve by changing a single parameter, thereby facilitating opportunities to iteratively revise and refine multiple attempts in the same time span in which a student would have drawn one attempt by hand a couple decades ago. Moreover, coupled with the network of calculators and computers, the cross-pollination of ideas proceeds at a rapid pace, turning learning truly into a process that is social and mathematical at the same time.

Wallace (2004) pointed out that educators  know more about how to incorporate technology into the curriculum, in general, and about software that affects student learning than about the teacher’s role in using technology for achieving student understanding, in particular, regarding subject matter. In this study, we were able to see how technology facilitates the use of public space to gain a window into individual student thinking in a dynamic way. In particular, by following how each student’s contributions in relation to the preceding responses of the rest of the participants and contrasting with others’ submissions, the teacher can decide whether the proposed change is merely a minor modification of what came before or something altogether qualitatively different.

Both of these approaches give the teachers different resources to use in follow-up discussions or to address through instruction based on students’ previous understanding. For example, by looking at the public space as it was being populated by students’ submission of equations, the teacher was able to characterize, practically in real time, different clusters.

By identifying particular equations, the teacher highlighted these expressions and generated a class discussion to validate their accuracy, for example, those of the type of equations with parameters (a,b): (49,-0.45), (50,-0.45), (49,-0.49):

Students’ justifications allowed the teacher to assess student understanding of the (identified) mathematical structure of the submitted equations.

Though students provided a broad variety of approaches to find a curve of best fit, none of the students utilized Lagrange’s interpolation to generate their equations. Yet, they used mathematical ideas of continuity and precision, and some students negotiated the tensions they perceived between the two. Without engaging in a discussion on the appropriateness of the following pedagogical approaches, continuity is often heuristically introduced to students by saying “when you draw the curve, you can’t lift your pencil from the paper.” This is important. It has nothing to do with the question of whether a function can be written down in one single expression or several. Surely the following function is continuous despite the fact that it requires several mathematical expressions to describe it:

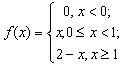
By contrast, differentiability is heuristically characterized by drawing a smooth curve, or a curve with no kinks. The teacher’s assessment of student thinking throughout the course helped her realize that, as a rule of thumb, students often pick up on the fact that the functions described by a single equation generally have a smooth graph, at least in most textbook examples. Thus, where students sought a solution in terms of an easily expressible function, they seemed to be conflating differentiability with continuity.

Conclusion

This paper has provided an example of a generative activity using network-based technology to provide a dynamic public space that captures student-to-student interaction and is guided by an instructor. The particular technology in place provided a system by which students could explore their own ideas in mathematical form in order to solve a problem in a personal space, while at the same time receiving ideas and feedback from their peers through a public space. For the teacher, the records created by the technology provided a tool to investigate how a particular student’s public space evolved over the course of the activity and, therefore, provided the teacher with a new avenue to reconstruct student’s dynamic understanding of the concepts discussed: emergent public and personal spaces.

While the three groups made similar use of these social interactions in the development of knowledge when participating in the given generative activity on function interpolation, our results provide evidence of different mathematical spaces generated by the three groups. There were some similarities in the characterization of the equations submitted by the three groups, as they all used quadratics, as well as equations of the form

.

However, Groups 2 and 3 generated mathematical spaces with similar structure as they used piecewise-defined functions; whereas Group 1 did not use piecewise-defined functions, but did make use of trigonometric functions in their public space.

The preservice teachers in Groups 2 and 3 generated a qualitatively different mathematical space than the nonpreservice teachers in Group 1. Yet, the three groups evidenced rich mathematical structures that were productive in the learning of function interpolation. The goal of integrating this function elicited students’ ideas of accuracy and continuity that were differently addressed by the groups.

In addition, students’ participation in this activity provided an experience of a transformation of the learning environment and a reconceptualization of the mathematical content that emerged.

In particular, this activity “provided opportunities for preservice teachers to themselves learn in and reflect upon facilitating effective learning” (Shamatha, Peressini, & Meymaris, 2004, p. 375). This experience can become an opportunity to experience innovative ways of teaching and learning mathematics in their preparation as future teachers if incorporation of new technologies is to be seen as a catalyst for generating new classroom interactions that allow for reconceptualizations of mathematical content and social spaces. As Brown (2002, p. 153) described, “It is only by acting in the world and thus changing the world that we learn how to act in the world.”

References

Ares, N., Stroup, W. M., & Schademan, A. R. (2009). The power of mediating artifacts in group-level development of mathematical discourses. Cognition & Instruction, 27(1), 1-24.

Asiala, M., Cottrill, J., Dubinsky, E., & Schwingendorf, K. E. (1997). The development of students’ graphical understanding of the derivative. Journal of Mathematical Behavior, 16, 399-431.

Aspinwall, L., Shaw, K. L., & Presmeg N. C. (1997). Uncontrollable mental imagery: Graphical connections between a function and its derivative. Educational Studies in Mathematics, 33, 301-317.

Black, P., & Wiliam, D. (1998a). Inside the black box: Raising standards through classroom assessment. Phi Delta Kappan, 80(2), 139-144, 146-148.

Black, P., & Wiliam, D. (1998b). Assessment and classroom learning. Assessment in Education: Principles, Policy & Practice, 5(1), 7-74.

Brown, T. (2002). Mathematics education and language: Interpreting hermeneutics and post-structuralism. Dordrecht, Netherlands: Kluwer.

Cantoral, R., & Montiel, G. (2003). Una presentación visual al polinomio de interpolación de Lagrange. Números,  55, 3-22.

Carpenter, T. P., Fennema, E., Franke, M. L., Levi, L., & Empson, S. B. (1999). Children’s mathematics: Cognitively guided instruction. Portsmouth, NH: Heinemann.

Clark-Wilson, A. (2010). Emergent pedagogies and the changing role of the teacher in the TI-Nspire Navigator-networked mathematics classroom. ZDM, 42(7), 747-761.

Davis, R. B., & Vinner, S. (1986). The notion of limit: Some seemingly unavoidable misconception stages. The Journal of Mathematical Behavior, 5, 281-303.

Eisenberg, T. (1991). Functions and associated learning difficulties. In D. Tall (Ed.), Advanced mathematical thinking (pp. 140-152). Dordrecht, Holland: Kluwer.

Ferrini-Mundy, J., & Graham, K. (1994). Research in calculus learning understanding of limits, derivatives and integrals. Research Issues in Undergraduate Mathematics Learning, MMA Notes, 33, 31-45.

Filer, A. (1993). Contexts of assessment in a primary classroom. British Educational Research Journal, 19, 95-107.

Habre, S., & Abboud, M. (2006). Students’ conceptual understanding of a function and its derivative in an experimental calculus course. Journal of Mathematical Behavior, 25, 57-72.

Janvier, C. (1987). Representation and understanding: The notion of function as an example. In C. Janvier Problems of representation in the teaching and learning of mathematics. (pp. 67-70). Hillsdale, NJ: Erlbaum.

Juter, K. (2006). Limits of functions as they developed through time and as students learn them today. Mathematical Thinking & Learning, 8(4), 407-431.

Kersaint, G. (2007). Toward technology integration in mathematics education: A technology integration course planning assignment. Contemporary Issues in Technology and Teacher Education, 7(4), 256-278.

Kieran, C. (1997). Mathematical concepts at the secondary school level: The learning of algebra and functions. In T. Nunes & P. Bryant (Eds.), Learning and teaching mathematics: An international perspective (pp. 133-158). East Sussex, UK: Psychology Press.

Malik, M. A. (1980). Historical and pedagogical aspects of the definition of function. International Journal of Mathematical Education in Science and Technology, 11(4), 489-492.

Millspaugh, R. P. (2006). From intuition to definition: Teaching continuity in first semester calculus. Primus: Problems, resources, and issues in mathematics undergraduate studies, 16(1), 53-60.

Newmann, F. M. (1992). The assessment of discourse in social studies. In H. Berlak, F. M. Newmann, E. Adams, D. A. Archbald, T. Burgess, J. Raven, & T. A. Romberg (Eds.), Toward a new science of educational testing and assessment. (pp. 53-69). Albany, NY: State University of New York Press.

Núñez, R., Edwards, L., & Matos, J. F. (1999). Embodied cognition as grounding for situatedness and context in mathematics education. Educational Studies in Mathematics, 39(1-3), 45-65.

Orton, A. (1983). Students’ understanding of integration. Educational Studies in Mathematics, 14(1), 1-18.

Rasmussen, C., & Stephan, M. (2008). A methodology for documenting collective activity. In A.E. Kelly, R. A. Lesh, & J. Y. Baek (Eds.), Handbook of design research methods in education: Innovations in science, technology, engineering, and mathematics learning and teaching. (pp. 195-215). New York, NY: Routledge.

Rasslan, S., & Tall, D. (2002). Definitions and images for the definite integral concept. In Anne D. Cockburn & Elena Nardi (Eds), Proceedings of the 26th conference of the International Group for the Psychology of Mathematics Education, 4, 89-96.

Shamatha, J. H., Peressini, D., & Meymaris, K. (2004). Technology-supported mathematics activities situated within an effective learning environment theoretical framework. Contemporary Issues in Technology and Teacher Education, 3(4), 362-381. Retrieved from https://citejournal.org/vol3/iss4/mathematics/article1.cfm

Sierpinska, A. (1987) Humanities students and epistemological obstacles related to limits. Educational Studies in Mathematics, 18, 371-397.

Skovsmose, O. (1998). Book review: Mathematics education and language: Interpreting hermeneutics and post-structuralism (by Tony Brown). ZDM, 98(5), 138-41.

Stewart, J. (2003). Calculus (5th ed.). Belmont, CA: Thomson.

Stroup, W. M., Ares, N. M., & Hurford, A. C. (2005). A dialectic analysis of generativity: Issues of network-supported design in mathematics and science. Mathematical Thinking & Learning, 7(3), 181.

Stroup, W., Carmona, G., & Davis, S. (2005). Improving on expectations: Preliminary results from using network supported function based algebra. In G. M. Lloyd, M. Wilson., J. L. Wilkings, y S. L. Behm (Eds.), Proceedings of the 27th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education.  Roanoke, VA: Psychology of Mathematics Education.

Stroup, W. M., Ares, N. M., Hurford, A. C., & Lesh, R. A. (2007). Diversity-by-design: The why, what, and how of generativity in next-generation classroom networks. In R. A. Lesh, E. Hamilton, & J. J. Kaput (Eds.), Foundations for the future in mathematics education (p.367-393). Mahawah, NJ: Lawrence Erlbaum.

Stroup, W., & Davis, S. (2004). Generative activities and function-based algebra. In H. L. Chick & J. L. Vincent (Eds.), Proceedings of the 29th annual meeting of the International Group for the Psychology of Mathematics Education (Vol.1, p. 328). Melbourne, Australia: Psychology of Mathematics Education.

Tall, D., & Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limit and continuity. Educational Studies in Mathematics, 12, 151-169.

Thompson, P. W. (1994). Students, functions, and the undergraduate curriculum. In E. Dubinsky, A. H. Schoenfeld, & J. Kaput (Eds.), CBMS Issues in Mathematics Education: Research in Collegiate Mathematics Education I, 4, 21-44.

Thompson, P. W., & Silverman, J. (2008). The concept of accumulation in calculus. In M. Carlson & C. Rasmussen (Eds.), Making the connection: Research and teaching in undergraduate mathematics (pp. 117-131). Washington, DC: Mathematical Association of America.

Ubuz, B. (2007). Interpreting a graph and constructing its derivative graph: stability and change in students’ conceptions. International Journal of Mathematical Education in Science and Technology, 38(5), 609-637.

Wallace, R. M. (2004). A framework for understanding teaching with the Internet. American Educational Research Journal, 41(2), 447-488.

Wagner, S. (1981). Conservation of equation and function under transformations of variable. Journal for Research in Mathematics Education, 12(2), 107-118.

Author Information

This research study would not have been possible without the support of the Oak Ridge Associated Universities (ORAU) in the form of the Ralph E. Powe Junior Faculty Enhancement Award; the support of the Tecnológico de Monterrey (ITESM) for the project CAT108; and the support of Texas Instruments, Dr. Walter Stroup and the Models and Modeling Research Group at the University of Texas at Austin. We would also like to thank our editor, Christine Brown, and three anonymous reviewers for their helpful feedback on this manuscript.  The views here expressed are those of the authors and not necessarily of the funding agencies.

Guadalupe Carmona
The University of Texas at Austin
email: [email protected]

Angeles Domínguez
Tecnológico de Monterrey
email: [email protected]

Gladys Krause
The University of Texas at Austin
email: [email protected]

Pablo Durán
The University of Texas at Austin
email: [email protected]