Typically, students view mathematical proof as an academic exercise required to pass a course. Mathematicians value proof as a form of explanation and validation. Teachers should promote proof writing as a means to explain and communicate mathematics. In 1989 the National Council of Teachers of Mathematics (NCTM) published the Curriculum and Evaluation Standards for School Mathematics. A total of 10 process and content standards were identified, including communication and reasoning. These recommendations written over 20 years ago are still relevant as educators strive to engage students as doers of mathematics.
Emphasizing communication in a mathematics class helps shift the classroom from an environment in which students are totally dependent on the teacher to one in which students assume more responsibility for validating their own thinking. (Grades 5-8, p. 79)
Reasoning is fundamental to the knowing and doing of mathematics. Although most disciplines have standards of evaluation by which new theories or discoveries are judged, nowhere are these standards as explicit and well formulated as they are in mathematics. Conjecturing and demonstrating the logical validity of conjectures are the essence of the creative act of doing mathematics. To give more students access to mathematics as a powerful way of making sense of the world, it is essential that an emphasis on reasoning pervade all mathematical activity. Students need a great deal of time and many experiences to develop their ability to construct valid arguments in problem settings and evaluate the arguments of others. (Grades 5-8, p. 81)
In the study reported here, I investigated whether or not creating and sharing screencast proofs would help students value geometric proofs as a means to explain and communicate important mathematics. The purpose of this paper is to present research results from student-created screencasts that engaged students in proof writing, as well as proof editing.
The elementary education majors worked in pairs to complete one problem from a specific set of proofs on either congruent or similar triangles produced by reflection. The assigned problems were situated in a real world context in which distances were required. Students were then required to explain why their computation was valid by completing the proof. The context of similar and congruent triangles is found in the NCTM (2008) Grade 8 focal point for geometry and measurement:
Analyzing two- and three-dimensional space and figures by using distance and angle
Students use fundamental facts about distance and angles to describe and analyze figures and situations in two- and three-dimensional space and to solve problems, including those with multiple steps. They prove that particular configurations of lines give rise to similar triangles because of the congruent angles created when a transversal cuts parallel lines. Students apply this reasoning about similar triangles to solve a variety of problems including those that ask them to find heights and distances. They use facts about the angles that are created when a transversal cuts parallel lines to explain why the sum of the measures of the angles in a triangle is 180 degrees, and they apply this fact about triangles to find unknown measures of angles. Students explain why the Pythagorean theorem is valid by using a variety of methods – for example, by decomposing a square in two different ways. They apply the Pythagorean theorem to find distances between points in the Cartesian coordinate plane to measure lengths and analyze polygons and polyhedra. (p. 20)
This paper contains four sections. The first section will present the theoretical framework for the research study and review supporting literature. The second section will present the research methodology utilized in this study. The third section will present an analysis of three student screencasts, highlighting the classroom discussion that took place during the peer review process as well as research findings. Section 4 contains a discussion of the results, elements of my action plan, and suggestions for future research.
Frameworks and Literature Review
The Association of Mathematics Teacher Educators (AMTE, 2009) recently released the Mathematics TPACK (Technological, Pedagogical and Content Knowledge) Framework. This framework was developed for the purpose of guiding educators in the essential elements of mathematics learning experiences with technology. The framework is composed of four major areas: development and design of learning experiences, facilitation of instruction, the assessment of teaching and learning, and professional development (Figure 1). The Mathematics TPACK Framework was used as a tool to structure the reporting of the study since it supports my primary role of mathematics educator.
| Standard I. Design and develop technology-enhanced mathematics learning environments and experiences. Standard II. Facilitate mathematics instruction with technology as an integrated tool. Standard III. Assess and evaluate technology-enriched mathematics teaching and learning. Standard IV. Engage in ongoing professional development to enhance technological pedagogical content knowledge. |
| Figure 1. AMTE Mathematics TPACK Framework Standards. |
The framework for the design of the classroom activities also drew from literature on proof, the use of a dynamic geometry system, the emerging use of student-generated screencasts, and the practice of reflection and peer review. The theoretical frameworks used to interpret and analyze the students’ reflections and peer review were Bloom’s Digital Taxonomy (Churches, 2010) and the Mathematics Activity Learning Types (Grandgenett, Harris, & Hofer, 2009).
Proof
The NCTM (2000) Principles and Standards for School Mathematics recommended that proof be taught across content areas and age levels as part of the students’ mathematical experience. The Process Standard of Reasoning and Proof can be woven throughout the curriculum, as students explain why an achieved result or generalization is correct (or incorrect). Interestingly, the October 2009 issue of Mathematics Teacher (NCTM) was devoted to the theme of proof and included a range of articles on effectively integrating logic and proof into teaching practice. Cirillo (2009) summarized her top 10 things to consider when teaching proof; fourth on her list was to be more explicit about the purpose of proof. Getting caught up in teaching techniques and forgetting to attend to the purpose is easy. Cirillo reminded readers to convince and explain:
This distinction between convincing and explaining is important because, in many cases, there is little doubt in students’ minds that some particular proposition is true … However, students are so often asked to show or explain, so perhaps asking them to write a proof as a way of explaining why something is true would make more sense to them. [emphasis in original] (p. 253)
Students have been shown to struggle with proof writing, due to operating on a low van Hiele level (Senk, 1989). Students are often confused by the different formats of proof, since they can range from an informal argument to a rigorous justification. In many cases, students often have trouble negotiating what is acceptable (Dreyfus, 1999). Educators have established multiple purposes for proof writing, including explanation, systematization, communication, discovery, justification, intuition development, and autonomy (Webber, 2003).
The functions of proof as explanation and communication (deVilliers 2003; Knuth, 2002) were identified as the primary focus for this action research project. When working with preservice teachers, the mathematics educator is challenged to model instruction that imparts both the purpose and the mechanics of proof writing. The study reported here engaged preservice teachers in activities that fostered a classroom environment supporting the communication of proof. Technologies in the form of the dynamic geometry system and screencast software were used as tools to support the communication of a geometric proof to the preservice teachers’ peers.
A screencast is a video that captures the actions taking place on the computer screen, making screencasts a common tool for Internet-based training and instruction. Screencasts are generally accompanied by an audio track, recorded with an internal or external microphone that explains what is taking place in the video. The use of dynamic geometry has a rich history in mathematics education, and the use of screencasts is emerging as a tool for mathematics instruction.
The Dynamic Geometry System
A dynamic geometry system is a computerized setting in which figures can be either drawn or constructed. Shapes that are drawn without constraints will deform when the “drag test” is performed, while constructed figures will retain the requisite features of the construction. The role of the dynamic geometry system has been firmly established in the mathematics education research literature (Hollebrands, Laborde, & Sträßer, 2009). Battista and Clements (1995) explain the merits of dynamic geometry systems for supporting student investigation and sense making. The researchers situated their discussion in the context of Piaget’s stages of development and the van Hiele levels of reasoning. They concluded that teachers should move away from the traditional goal of teaching formal proof writing in order to establish certainty to a goal of facilitating the students’ progression from conjecture to valid justification:
Ironically, the most effective path to engendering meaningful use of proof in secondary school geometry is to avoid formal proof for much of students’ work. By focusing instead on justifying ideas while helping students build the visual and empirical foundations for higher levels of geometric thought, we can lead students to appreciate the need for formal proof. Only then will they be able to use it meaningfully as a mechanism for justifying ideas. (p. 53)
Students need learning experiences that will support their future work with proof. Jones (2000) found that middle school students were better able to explain their classification hierarchy for families of quadrilaterals after working with Sketchpad activities that exposed the definitions of the various quadrilaterals. Goldenberg and Cuoco (1998) called attention to how students had to negotiate the necessary and sufficient conditions of a definition when working in the dynamic geometry system. The role that The Geometer’s Sketchpad plays in the student’s development of proof writing has been well established by de Villiers (2003). When students encountered empirical evidence and formed a conjecture, they began to see proof as a form of supporting explanation (de Villiers, 1998; Laborde, 2000; Mariotti, 2000).
The advantage of visualizing many examples at once was summarized in Lester’s (1996) dissertation (cited in Glass & Deckert, 2001), “The Geometer’s Sketchpad program allows students to manipulate diagrams easily, thereby freeing them to focus on the various relationships and patterns that are displayed on the screen and in the requested measurements” (p. 225). The themes of exploration and knowledge construction are linked to gains in student proof writing abilities and achievement (Chazan & Yerushalmy, 1998; deVilliers, 1998; Glass & Deckert, 2001).
The experience that students gain through visualization and the gathering of empirical evidence supports the need for formal deductive proof. Hoyles and Healy (1999) documented the existence of a gap between the making and believing of the conjecture in the dynamic geometry system and the formal action of proof writing using deductive reasoning. Christou, Mousoulides, Pittalis, and Pitta-Pantazi (2004) investigated the identified gap through the analysis of three students completing an open-ended problem on the midpoint quadrilateral of a kite. The problem was introduced as an open-ended task in order to avoid front-loading the student with the requirement of writing a formal proof. As a result, one student did not feel that a proof was necessary while the other two felt a need to continue with a proof for the purpose of explanation. The researchers documented student activity through interviews in the phase before the proof, the proof phase, and a phase of systematization to problems with similar reasoning. The use of the dynamic geometry system in the phase preceding the proof was integral as students constructed the kite and its midpoint quadrilateral, measured the component segments and angles, and then used the drag facility to test invariant properties. During the proof phase, the students used measurements they found and properties they noticed to determine theorems and definitions supporting a proof that the midpoint quadrilateral was indeed a rectangle.
Digital Media
The use of a student-generated screencast to explain mathematics is a relatively new endeavor. Marcos (2008) reported that he encouraged his sixth graders to use his tablet PC to author their own mathematics screencasts. He then uploaded the screencasts to his school website (http://www.mathtrain.com). He reported that his students were highly motivated to capture their mathematical knowledge on his tablet PC. Marcos and his students have since received international recognition for his work to facilitate kids teaching kids through screencast production.
Mathematics educators Kosiak and LeDocq (2008) describe how preservice teachers (PSTs) created interactive applets on a tablet PC to prepare other undergraduates for the state licensing examination on basic mathematics. The PSTs reportedly engaged the mathematics content at a much deeper level and, therefore, struggled to scaffold questions within the applets to promote investigation by the user.
Edwards (2008) reported on a project where PSTs illustrated and narrated mathematics stories in screencast format. Edwards documented the PSTs’ use of mathematical content and vocabulary as the PSTs wrote and recorded their stories. He noted that the process of writing and narrating the story was more important in the PSTs’ learning of mathematics than the product that was produced, due to the corrections that the students made to mathematical errors during the story writing process. In each of these conference sessions, students were using digital technology to produce mathematical artifacts. Motivation increased and ownership shifted as students focused on communicating mathematical knowledge.
As technology takes on an ever-increasing role in our society, educators are challenged to find ways to use technology for learning. The Digital Bloom’s Taxonomy (Churches, 2010) provides a reference as educators across all content areas negotiate what types of activities support higher order thinking skills. Notice the positions of creating and evaluating in the taxonomy (see Figure 2).
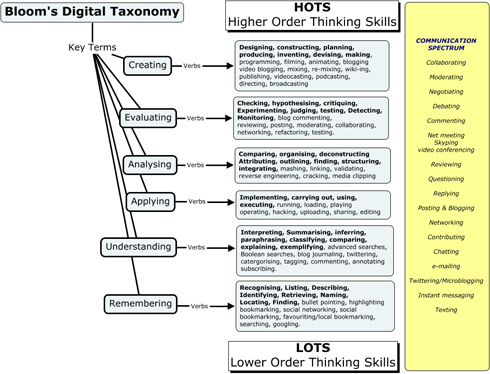
Figure 2. Bloom’s Digital Taxonomy Concept map from the Educational Origami website: http://edorigami.wikispaces.com/Bloom%27s+Digital+Taxonomy. Reprinted under the Creative Common License, Attribution-ShareAlike 2.5 Generic.
A similar taxonomy exists in the Mathematics Learning Activity Types (Grandgenett et al., 2009). The taxonomy focuses the teacher’s attention first on the activity type and then the various technologies that could be used to support the student action. The Mathematics Learning Activity Types, based on the NCTM (2000) process standards, are Consider, Practice, Interpret, Produce, Apply, Evaluate, and Create. Developing the screencasts can be categorized as both Produce and Create activity types as students “produced a representation” and “described an object or concept mathematically.” The self/peer review task fell under the Evaluate activity type.
Reflection and Peer Review
Reflection and peer review is often used in mathematics methods courses with preservice teachers in conjunction with a microteaching episode. With microteaching, the PSTs typically prepare a lesson and teach a segment of the lesson to their peers. Assessment of the microteaching begins with comments by PSTs on what they felt went well and what they identified as an area for improvement. Once the self-critique is completed, peers provide feedback that is balanced between what went well and what needs improvement. We commonly videotape the microteaching for the purpose of self- or peer evaluation. The goals of assessing the taped teaching episode are balanced between the evaluation of the PSTs’ teaching practice and as a learning experience for the PST. I incorporated the use of self- and peer evaluation within the context of a mathematics content course to foster a learning experience and class discussion similar to the analysis of a microteaching episode.
The action research study completed by Zevenbergen (2001) articulated my goal of using peer assessment as a tool for learning. Zevenbergen’s 4-year study focused on the use of peer assessment as preservice teachers evaluated their classmates’ mathematics posters. Students created a poster on a mathematics topic that could contain up to 25 words. Students also created the criteria for assessment: visual impact, mathematical content, and adherence to the word count limit. “Because students had been involved in the construction of their own posters and were personally aware of the decisions they needed to make, they were more critical of the decisions made by their peers” (p. 107). Zevenbergen went on to report that through the examination of the posters, her students were exposed to aspects of the mathematics curriculum that were unfamiliar to them, and they were able to see that the same content could be displayed in a variety of ways. The screencast proof assignment reported in this study was similar in purpose. The goal was twofold, to use technology to communicate mathematics—the poster is replaced by the screencast—but also to use the created artifacts as a learning tool for reflective activity.
A review of the current literature on student reflection or self/peer assessment with video yielded results primarily in the field of sports. Leijen, Lam, Wildschut, Simons and Admiraal (2009) found that ballet students’ use of viewing their own performance on video was helpful in “developing a more realistic view of their dance experience” (p. 175). The researchers also noted that students were generally more receptive to comments generated by peers than by the dance instructor. While watching and listening to mathematics is much different than watching a ballet performance, the change in perspective would be similar. One ballet student described how watching the video helped her to “consider the work from the audience perspective” (p. 173). This result points to the role of self-assessment in mathematics and the use of technology as a vehicle to encourage students to consider how the potential reader will follow a proof they authored.
The use of a dynamic geometry system, the emerging use of student-generated screencasts, and the practice of reflection and peer review provided the framework for the development of classroom activities that would support an investigation of the following research question. How does the use of technology impact the task of writing and reviewing formal proofs with the purpose of explaining and communicating mathematics? The implementation and results of the classroom activities were investigated through an action research methodology.
Action Research Methodology
Action research is a systematic study of an identified phenomenon in the teacher’s classroom or educational setting (Ferrance, 2000). The research results are specific to the teacher and students in the setting and are used to inform future instruction in the form of an action plan. Multiple data sources are analyzed to establish trustworthiness in the reported narrative. In my role as a teacher-researcher, I designed a sequence of tasks, facilitated the instruction, collected the students’ assignments from the self/peer review process, videotaped the class discussion of two of the screencasts, analyzed the data, and created an action plan. The analyzed data included the individual screencast proofs, student notes, videotape of the class discussion, and teacher notes. Mathematics TPACK Framework Standards I through III were used to structure the remainder of this section.
The Student Tasks
Mathematics TPACK Framework Standard I. Design and develop technology-enhanced mathematics learning environments and experiences.
Establish and utilize mathematical environments, tasks, experiences and resources to integrate technology tools that support learner’s individual and collaborative mathematical learning and creativity. (AMTE, 2009, p. 1)
The study reported in this paper took place in a geometry content course for elementary education majors enrolled in a medium-sized midwestern university. The class included 2 male and 9 female students, ranging from sophomores to seniors. Since these students were concentrating in mathematics, they were required to take additional coursework in mathematics. In the spring 2009 geometry content course, students used The Geometer’s Sketchpad program to explore properties of quadrilaterals as they worked toward the goal of proof and justification that incorporated the use of the triangle congruence postulates. The topic of similar triangles was introduced through the task of finding the measurement of a light pole. Students worked in teams to measure triangle segments created by shadows or triangle segments created by a mirror on the ground (they also used a clinometer, which is a protractor with an attached straw and weight). The measurements were used to approximate the height of a light pole.
At the beginning of the semester, I received unanimous consent to collect data for an action research study from students enrolled in the geometry course. The human subjects protocol allowed for the collection of student work produced as part of normal class attendance, teacher notes and lesson plans, and videotape of selected class sessions. After grades were posted, I learned that all students had given consent for their work to be published. Students also gave consent for their real names to be used.
This action research study took place immediately following the measurement activity. The instructional goal was to transition from using the results of similar triangles (to find a height) to understanding and explaining why the proportions used were valid. The screencast project included four distinct tasks. Work completed by two students, Brittany and Diana, illustrates the first two tasks.
Task A: Illustrate your assigned problem and create the visual illustration of its proof. Brittany and Diana, used The Geometer’s Sketchpad to model the problem of finding the height of a flagpole using the shadow technique (see figures 3 and 4 later in this paper). They created a sketch of the two similar triangles and measured the required sides. They calculated a scale factor that would relate their model to realistic measurements. Brittany and Diana used hide/show buttons to layer the information that needed to be presented for both the calculations and the proof. Most students completed Task A during class time. The research artifacts produced from Task A were The Geometer’s Sketchpad files. The source for each of the assigned problems is Exploring Geometry with Geometer’s Sketchpad (Bennett, 2004). Appendix A outlines a list of the problems and students who completed them. Kourtney was asked to work individually, because the class had an odd number of students.
Task B: Narrate the Sketchpad proof with Jing – Create a screencast. This task was completed outside of class. Most student pairs met and worked together on the screencasts, but since Brittany and Diana both commuted to campus, they created two screencasts, one for the proof and one for the computation (Jackie and Lindsey also created two screencasts; see Appendix B). Students used the Jing program as a tool to narrate the text and animations in their Sketchpad file. Jing produces a Shockwave Flash file (with a swf extension) that can be opened through a browser. Since Jing is freeware, the user is limited to a 5-minute clip and has no access to editing features. The screencasts became an artifact for the study.
Task C: Watch all of the screencasts, noting strengths and weaknesses. Once the screencasts were completed and submitted, they were posted to the university’s Blackboard course management system. Students were asked to view and document both the strengths and weaknesses of each of the screencasts. The handwritten student documentation was collected as an additional research artifact.
Task D: In-class discussion of self/peer review of screencast proofs. The final task in this sequence was the whole class discussion of the screencast proofs. After each screencast was viewed, the student authors were asked to talk about what they noticed in the work they had produced. Once the student pairs had an opportunity to share, the discussion was opened up to the rest of the students, then to the teacher. Data was collected in the form of teacher-researcher field notes. Also, a video recording of the whole class discussion of two of the screencasts was made for post hoc analysis.
The Teacher-Researcher
Mathematics TPACK Framework Standard II. Facilitate mathematics instruction with technology as an integrated tool.
- Facilitate technology-enriched, mathematical experiences that foster creativity, develop conceptual understanding, and cultivate higher order thinking skills.
- Promote mathematical discourse between and among instructors and learners in a technology-enriched learning community.
- Encourage learners to become responsible for and reflect upon their own technology-enriched mathematics learning. (AMTE, 2009, p. 2)
In a synthesis of the research on how technology is used by teachers and learners, Zbiek and Hollebrands (2008) identified various roles and responsibilities teachers assume during instruction. The authors cited three key works that delineated teacher roles in technology-using mathematics classrooms: Fraser, Burkhardt, Coupland, Philips, Pimm and Ridgway (1988), Farrell (1996), and Heid, Sheets, and Matras (1990). Teacher roles, listed in alphabetical order, included Allocator, Catalyst and Facilitator, Collaborator, Counselor, Evaluator, Explainer, Manager, Planner and Conductor, Resource, Task Setter, and Technical Assistant. Within the screencast project, the role of the teacher transitioned from the Explainer to Counselor and then to Manager.
Explainer. “The teacher demonstrates, establishes the context, focuses the classroom direction, and serves as rule giver and knowledge source” (Zbiek & Hollebrands, 2008, p. 299). The screencast project was the last set of assignments for the semester. Students were allowed to select which problem they would work on and, essentially, whom they would work with. During class time, I modeled the first two tasks. I created a Sketchpad file illustrating that the sum of the measures of the angles of a triangle is 180 degrees. Animation was used to show the rotation of the base angles. I then introduced the students to Jing by creating a screencast of the triangle sum theorem. The proof screencast was replayed so the finished product could be discussed. After modeling and outlining the four tasks, my role shifted to that of a counselor.
Counselor. “The teacher is familiar with the problem and is able to advise and assist students when they ask for teacher input. This role includes playing the devil’s advocate, as well as providing encouragement or serving as a stimulator or diagnostician” (Zbiek & Hollebrands, 2008, p. 299). Although none of the students asked for help with Jing, a few students had questions about their proofs. Instead of directly answering questions, I asked students where they had seen something similar or assisted by simply validating student work.
Manager. “Teacher serves as tactical manager, director, and authoritarian” (Zbiek & Hollebrands, 2008, p. 299). In the class session where the self/peer reviews were shared with the class, the role of the teacher shifted to manager in order to sequence and coordinate the discussion of the screencast proofs, since there were specific points that needed to be reached in a short amount of time. An interesting shift of authority occurred during the classroom discussion and will be articulated later in this paper.
Assessment
Evaluation and assessment of student learning serves the purpose of benchmarking student progress toward the instructional goals as well as providing information that can be used to improve instruction. In this action research study, the assessment was intensified after the artifacts were examined for patterns or themes that might impact my teaching cycle in real time.
Mathematics TPACK Framework Standard III. Assess and evaluate technology-enriched mathematics teaching and learning.
- Use of formative assessment of technology-enriched lessons and activities to evaluate mathematics learning and adjust instructional strategies accordingly.
- Evaluate and reflect on the effective use of existing and emerging technologies to enhance the mathematical learning of all. (AMTE, 2009, p. 2)
The initial assessment took place when the screencasts were submitted for peer review and was formative in nature. The screencasts were first assessed for accuracy of the mathematics content since students typically make mistakes when writing formal proofs. The primary focus was to evaluate the screencasts in order to manage the upcoming self/peer review class discussion. The second instance of formative assessment took place during the self/peer review class session. The class discussion was assessed in real time. I noted what students commented on in each of the screencasts to ensure that mathematical flaws or misunderstandings were addressed. A final round of assessment took place after instruction was completed, as part of the formal action-research cycle.
I reviewed the individual screencast proofs, student notes, videotaped class discussion, and teacher notes. The student notes contained their description of the strengths and weaknesses of each of the screencast proofs. The student notes were compared to what the students shared during the class discussion. The retrospective analysis looked at each of the screencast proofs separately and then as a whole to document any emerging patterns in the students’ use of The Geometer’s Sketchpad and the proofs they had written. The analysis also looked for common themes that were noticed by the students as they reviewed each other’s screencasts.
Results
After viewing each screencast numerous times, I documented strengths, such as the use of animation to show a reflection or the transition of segments to color-coded lines, which illustrated where parallel lines had been cut by a transversal. Also identified were a number of flaws in each of the screencasts. These flaws were common errors made by novice proof writers and were to be expected. Minor flaws included typographical errors or saying the wrong word during the screencast narration, while more serious flaws included a missing step in the proof or a logic error.
Careful listening during the in-class discussion was necessary, so the students could be prompted to find one of the flaws, if appropriate. The screencasts were sequenced for the class discussion with regard to problem type and the type of errors that were noted, leaving the proofs with more serious flaws for the end of the class session.
The class discussion of the screencasts progressed as projected, until a few students began to point out flaws I had not identified. The classroom atmosphere was one of excitement, because the students took on the role of authority as they explained what they had found. As the class discussion progressed, we noticed that it was rare if one person caught all the flaws in a screencast, which validates the use of multiple reviewers in the peer review process. At the conclusion of the class discussion, students were asked which screencast best communicated the assigned computation and proof. When they selected Kayla’s, it forced me to look at the assignment from the students’ perspective, to see what they were noticing.
Eleven students completed a total of six proofs. Specific strengths or errors for three of the proofs are presented from a synthesis of the student notes collected on the day of the peer review activity, as well as from two video clips recorded with a stationary video camera. Each of the screencasts can be viewed by clicking on the URL provided. Footage from the class discussion of the Side Splitter screencast and the Wall Mirror screencast are also available online. (Editor’s Note: Video URLs can be found in the Resources section at the end of this paper.)
Height of a Telephone Pole With Shadows
The team of Brittany and Diana completed an application and proof, which found the height of a telephone pole using shadows. Since both of these ladies commuted to campus, they divided their screencast into two clips (figures 3 and 4). Students liked how Brittany showed each step in the proof and how the sun’s angle was illustrated with the parallel lines. In the proof, students noted the following:
- The proof included the angle measurements and that these should be omitted.
- The audio track and the text should say that lines are perpendicular, not angles.
- The order of the points in the right angle’s labels was not consistent.
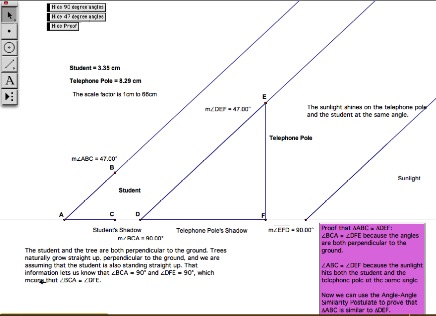 Figure 3. Last frame in the Shadow Proof screencast (Video 1).
Figure 3. Last frame in the Shadow Proof screencast (Video 1).
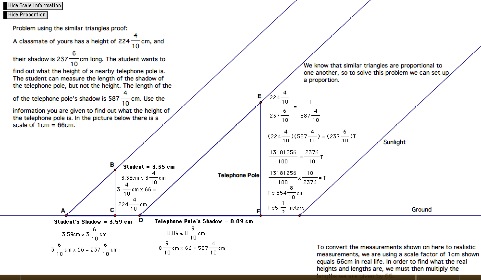 Figure 4. Last frame in the Shadow Math screencast (Video 2).
Figure 4. Last frame in the Shadow Math screencast (Video 2).
The errors contained within this example are important, because each of the mistakes the students noted are relatively common when writing and talking about geometric proofs. Students often use the actual angle measure in the proof, because they are making the transition from empirical evidence to a general case. Also, students do not pay careful attention to the way they use vocabulary. The last concern with the proof portion of this problem was that the order of the points in the right angle’s labels might be incorrect. Although the notation used here is mathematically correct, because the vertex is in the middle of the angle’s label, everyone agreed that the order could be reversed for clarity since vertex B matches with vertex E in the similar triangles. Failure to match up the corresponding vertices is another common mistake when stating that triangles are congruent or similar, so the fact that this was a discussion point showed attention to this important detail. A discussion of the computation portion (Figure 4) of the shadow problem follows.
Diana found the actual height of the telephone pole in the screencast she produced. The students liked how she found and used the scale factor of 1 cm to 66 cm but noted that she should have used a colon instead of the equal sign in her text. Diana converted all of the decimal entries to fraction notation. Although this step is not necessary in the metric system, she added it in response to a week’s worth of class discussion on converting decimal answers in the standard system to the appropriate fraction of a foot or inch. For example, students were asked to write 5.5’ as 5 1/2’ (or 5.4” as 5 3/8”) because of the common error pattern of simply using the digit in the tenths place as the number of inches (or fraction of an inch). This created an “aha” moment for Diana in regard to convention in the measurement systems. Concepts stressed in one mathematical situation could be incorrectly generalized to another setting.
Side-Splitter Theorem
Kourtney was challenged to not only work alone but to create an application for the Side-Splitter Theorem (Figure 5). This theorem states that if a triangle is intersected with a line parallel to one side, the remaining sides will be split proportionally. Since our school is located in the Midwest, Kourtney created a farming application. Corrections that Kourtney and the students found include the following:
- The step in the proof that used alternating interior angles should be corresponding angles. This error was due to Kourtney copying a mistake I had made when outlining this proof during class.
- At times the terms (and symbols) for similar and congruent were switched or congruent was used when she meant to say proportional. It appears that she was looking at the congruent angles when she meant to be talking about the similar triangles (the AA similarity step).
- She did not find the actual length of the fence.
- Kourtney’s use of “the same angle” in the third step of the proof is consistent with the text used in the course, while the more formal reason would be to use the Reflexive Property.

Figure 5. Last frame in the Side-Splitter screencast (Video 3).
Overall, the students liked this screencast the best. First, they felt that Kourtney’s use of the features of Sketchpad helped illustrate the proof. Her screencast highlighted the parallel lines and the transversal, and she translated an angle to illustrate congruent corresponding angles. The students also felt that the mistakes in the audio track were ones that are commonly made, and students should easily recognize them.
Students commented that they liked the listing of the proof steps on the right side of the screen and that the general layout and algebra steps were easy to follow. The students noted each occasion where the terms or symbols for congruence and similarity were switched. This is an easy mistake to make since similar triangles have congruent angles. It appeared that the students made their decision based on aesthetic features of The Geometer’s Sketchpad as opposed to the mathematical knowledge communicated.
An interesting portion of Kourtney’s screencast proof was the tentative transition from triangles being similar to the algebraic proportion. I replayed the section of the screencast where Kourtney said, “By using the similarity postulate we can speculate that x over (x + y) equals z over (z + w).” Kourtney was asked if she could do more than speculate about this. Class discussion focused on the fact that a constant ratio is part of the definition of similar figures. This activity indicated that Kourtney may have lost her confidence in the validity of the proof at the step where the algebraic proportion could be justified by the definition of similar triangles. See Video 4 for the class discussion of Kourtney’s proof.
The last screencast discussed in this section was more sophisticated with respect to the features of Sketchpad used, and the error was subtle.
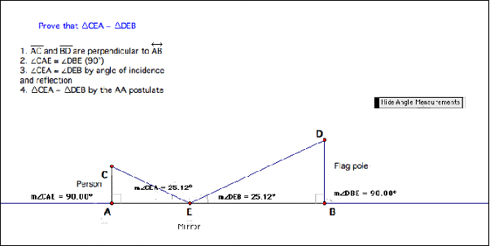
The Mirror Problem
The mirror problem challenged Casey and Jamie to find the minimum length of a wall mirror that would reflect a person’s entire image and supply the proof using deductive reasoning (Figure 6). An alternate proof strategy for this problem can be found in Navigating Through Geometry in Grades 9-12 (NCTM, 2001). As the students watched the screencast proof, many of them noticed the care Casey and Jamie used to document and explain each step. After viewing this particular proof, Jamie and Casey noted that there was a flaw in the proof. The flaw was not mentioned during the peer review discussion, so the proof section of the screencast was reviewed.
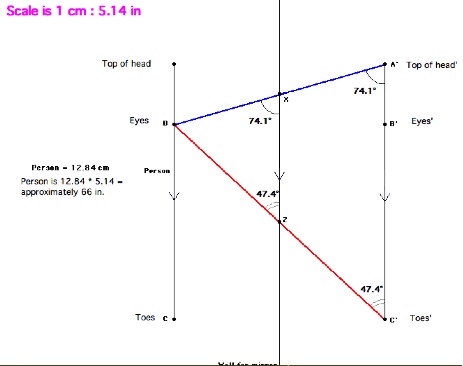 Figure 6. Screen shot of Wall Mirror screencast (Video 5).
Figure 6. Screen shot of Wall Mirror screencast (Video 5).
The screen shot in Figure 6 indicates the method used by Casey and Jamie as they established similar triangles BXZ and BA’C’. Color and tic marks were used as well as the duplicate page feature to show the sequence of steps in the problem. The proof was used to explain the final answer as the students discovered a ratio of 1:2 between triangles BXZ and BA’C’. The flaw in the reasoning can be noticed in the screencast section transcribed here. “Because the image is a reflection, every point is the same distance from the mirror. So, therefore, ![]() and
and ![]() .”
.”
These two sets of segments are congruent but not due to reflection. Point A’ is not the image of point B. Casey knew this, and the audio track of the in-class discussion suggests her doubts about this particular step in the problem when she said, “It’s not right.” After this section of the screencast was replayed for the class, Casey was asked to describe her thinking. Her response was that she just knew the step was wrong but not why it was wrong. By adding line segments AA’, AB’ and BB’ to the diagram that was projected on the white board, we were able to use the fact that the diagonals of a rectangle bisect each other so point X was the midpoint of segment BA’ (one possible remedy).
Figure 7 captures the markup that was completed during class. The class also discussed why this step was needed, and that it was not for the AA postulate but to find the measure of the length of the mirror. The class discussion of this screencast proof can be viewed in Video 6.
 Figure 7. Missing step in the proof.
Figure 7. Missing step in the proof.
Class Discussion
These students were highly engaged in the class discussion during the self/peer review class session. The students were proud of their work. They became focused on carefully listening to each word said, reading the text that had been provided, watching the animation in the Sketchpad files, and articulating what they had noticed. A somewhat heated debate took place, as Adam felt strongly that in these types of problems, the proof should precede the application. His reason was that, once his future students have the measurement, they would not care about a proof (many classroom teachers share this view). The screencast proof he and David completed on the Burning Tent Problem (Appendix C) illustrates this sentiment. Brittany and Diana also sequenced their screencasts so the proof would be followed by the computation.
As the students began to document the errors, they noticed that everyone had made a mistake or two. They noticed that a common mistake was to say congruent where the student meant to say similar, as well as use the congruent symbol instead of the symbol for similarity (~). No one offered an explanation as to why this was such a common error. They also noted instances in which triangles or angles had been mislabeled, since the corresponding parts of congruent or similar shapes must match up. When the flaw from the mirror proof was revealed, the group worked together to find a way to fix the proof. As a group, they began to appreciate the precise nature of mathematical language and said that this assignment helped them prepare for the final exam, since they were now able not only to write a proof, but also to evaluate the accuracy of a proof. Since students were required to write proofs for this project, I did not consider asking the students if they deemed proofs of their problems as necessary.
Emerging Themes
Three themes emerged in the retrospective analysis. First, some of the students had a strong opinion on whether the computation or proof should be initially presented. A second theme that emerged from the data was that students actively engaged in the evaluation of the artifacts produced by their peers. They noticed that each student pair made mistakes in the proofs but were able to find them and in most cases fix them. Third, the students valued the assignment, which was evident in the time and care they put into creating the Sketchpad files and Jing videos, as well as their level of engagement during the classroom discussion.
Discussion
The action research project reported here was conducted to investigate how the process of creating and reviewing the screencast proofs would impact students’ understanding of proof writing as a means to explain and communicate mathematics. Similar or congruent triangles provided a familiar context, since students understood how to use congruency or proportions to find a distance, but were not as comfortable in explaining why their computation techniques were valid. Results presented in this paper indicate that, as a group, the students were able to complete the proofs and identify the minor flaws. They were also able, when prompted, to remedy the more serious logical flaws.
The use of self/peer reflection of the screencast proofs repositioned assessment from what is traditionally between a student and the teacher closer to the student-student level. It also appeared that, after watching this series of proofs, the students who had been struggling with proof writing in general began to see an overall structure and procedure for this type of proof. Christou et al. (2004) referred to this transition as the “phase of systematization to problems with similar reasoning.” It appeared that, for this cohort, watching multiple examples helped them see an overall pattern in this family of proofs; that specific statements about segments and angles were necessary to support the use of a congruence (or similarity) postulate. Further research would be necessary to validate my suspicions. As a final step in the action research project, I formulated an action plan for future teaching. The action plan included two goals that were implemented in the spring 2010 geometry course. The following section will revisit the themes that emerged from the data through the lens of Bloom’s Taxonomy.
Themes
What comes first? The Burning Tent problem, the Feed and Water problem (Appendix D), and the Mirror problem had been previously completed as homework assignments with The Geometer’s Sketchpad. These students had used the properties of similarity or congruence to solve the problems (find the shortest path), but the task to explain why the given triangles were similar or congruent was completely different. Since the students were basically prompted to begin with the computation and then illustrate the proof, it was interesting that two of the six screencasts used a reversed order. Adam’s reason for positioning the proof before the computation was based on his pedagogical stance regarding his future students and what he thought they would perceive as important. Adam had evaluated the situation and could defend his position in an impromptu debate, which indicated he was operating at the highest levels of Bloom’s Taxonomy.
Evaluation of the screencast proofs. The students as a whole were effectively operating at the evaluation stage of Bloom’s Taxonomy as they completed the self/peer review. The students accurately exposed minor flaws across the set of proofs. Their attention to the order of vertices in triangle labels, their use of symbols and vocabulary, and their noticing a missing step in Adam’s proof of the Burning Tent problem illustrate the level at which they were analyzing the proofs.
The use of The Geometer’s Sketchpad may explain why specific angle measurements appeared in many of the students’ proofs. First, Sketchpad can easily find measurements, so students used this feature of the software because it was available. A second explanation would be that students thought that showing the angle measurements was a necessary part of the proof. For example, they may have felt that congruent angles should be documented for the reader in an attempt to be thorough. A third reason might be that they were simply comforted by seeing the measurements on the screen. They knew that if they moved one of the constructed points, corresponding angles would remain equal (as evident in a drag test). A final reason might be a lack of rigor in illustrating and writing the proof steps. This particular misconception appeared in a number of the screencasts. Apparently, the students were making a shift from including empirical evidence in a proof to writing a deductive proof based only on properties, definitions, and theorems.
Valuing the use of technology to communicate proof. As technology takes on an ever-increasing role in our society, educators are challenged to find ways to use technology to support learning. This assignment prompted students to make visible the transition between conviction and proof writing by asking them to compose and then illustrate a solution to an application problem and its supporting proof within the dynamic sketch. By positioning both the application and the proof within the electronic environment (in the same file), students were able to relate to the physical representation as they developed a justification. Students used the duplicate page feature, color, text boxes, and animation tools in addition to measurements of sides and angles in order to communicate their reasoning process.
Implementing the screencast project shifted the students’ role from passively completing a proof as an academic exercise to be graded by the teacher to decision maker and producer as they were planning, collaborating, animating, and filming. Requiring students to self-critique and peer-review their work empowered them as learners. These characteristics (producer, decision maker, collaborator, and evaluator) can be found at the highest levels of Bloom’s Digital Taxonomy, as well as in Grandgenett et al.’s (2009) Evaluate and Create activity types. A reference to the level of cognitive activity and the role of technology is found in the evaluate activity types section:
When students evaluate the mathematical work of others, or self-evaluate their own mathematical work, they utilize a relatively sophisticated understanding of mathematical concepts and processes. Educational technologies can become valuable allies in this effort, assisting students in the evaluation process by helping them to undertake concept comparisons, test solutions or conjectures, and/or integrate feedback from other individuals into revisions of their work. (Grandgenett et al., 2009, p. 5)
A review of the teacher notes from the classroom discussion indicated that these students valued the use of technology to communicate the mathematics. Students commented that the assignment was useful in helping them develop their own proof writing skills, because they knew what flaws to avoid. They also commented that they learned just as much or more from reviewing the screencast proofs their peers had created than from creating their own screencasts. Because the students were warned ahead of time that their screencasts would be shared with the class, they were comfortable with the peer review process.
Limitations
A limitation inherent to action research projects is the situated nature of the study to a single teacher’s classroom. The data that was collected and analyzed here is specific to these students and may not generalize to the population of preservice elementary education majors. A further limitation in this study is noted in the lack of student interviews as a data source to support the results. The screencast discussion took place on the last day of the semester, so it was not practical to schedule interviews with the students.
Action Research Plan
A key feature of action research is the development of an action plan based on results of the classroom investigation. I developed two goals for my action plan and implemented these goals in the spring 2010 geometry course.
1. Introduce Jing at the beginning of the semester as a tool to promote the voice of the student. Students were exposed to Jing as a communication tool early in the semester, but not required to use it. Over the course of the semester, a handful of students repeatedly used Jing to create screencasts as part of group presentations. As a result, the presentations captured the mathematical context and student’s narration. During presentations, students could reflect on the accuracy of what had been said. By using Jing, a focus on vocabulary was extended over the course of the semester.
2. Expand the use of self/peer review of artifacts to promote analysis and reflective activity. During the 2010 geometry course, selected assignments were published to my website for self- and peer review by the students. The first published assignment was a vocabulary project created in Sketchpad by teams of students and produced in a series of PowerPoint presentations (see videos 7, 8, 9, and 10). Students were asked to evaluate the text and illustrations of the assigned terms for accuracy. The assignment was revisited over a number of weeks as students were asked to refine the judgments they had made for each term. The objective was for students to identify a definition (or description of the undefined terms) as correct or incorrect (and fix the incorrect ones). This project was one of the students’ favorite activities of the semester, since it forced them to realize the impact of each and every word.
Another example of this goal was noted when I used the 2009 screencast proofs as a springboard for discussion. On the day that a number of the screencasts were viewed, the class discussion became animated, as different students demonstrated a willingness to explain a suspected flaw in the proof and how they would fix it. Even though this group of students had not created the screencast proofs, they actively engaged each other in the class discussion.
Future Research
The results of the action research reported here supports the need for further investigation on the use of screencast production of mathematics content and the self/peer evaluation of the mathematics artifacts. The use of technology motivated these students to communicate geometric proofs creatively to their peers. The peer/self assessment motivated these students to evaluate actively the accuracy of the mathematics explained in the proofs. As a result, I formulated two additional goals for my work as a teacher/researcher to support a more focused research methodology.
- Develop or locate a set of guidelines to provide more structure to the self-assessment and peer-assessment process.
- Develop or locate an interview protocol and interview students regarding the use of screencast production in mathematics class.
A suggested framework for future research might be to investigate if/how the process of creating and evaluating the screencasts impacts students’ memories. Sprenger, an educational consultant specializing in brain research applications, differentiation, and learning and memory (see http://www.brainlady.com), stated, “The brain has different memory systems that are activated by dissimilar types of triggers or cues. The systems include semantic, episodic, emotional, procedural, and conditioned response memory (Sprenger, 2005)” (quoted in Sprenger, 2010, p. 117). Sprenger also described how the process of creating a mathematics artifact, similar to the screencast project, impacts three different memory systems.
Digital natives follow procedures when they’re using computers and other digital devices. Will this kind of procedure trigger a procedural memory? It would seem that only a novel procedure would create such a memory. The brain habituates easily to repetitive tasks. When Germaine creates a PowerPoint presentation on quadratic equations for his math class, does the sequence of steps he uses to create the presentation help him remember the content? Quite possibly, but there is more than procedural memory at work. Choosing the background for his presentation may access episodic memory, as might the location where he created the PowerPoint presentation. As he practices his presentation, he may experience positive feelings of accomplishment if he feels he knows the material and is doing a good job, or negative feelings if he continually makes mistakes. Both of these situations may access emotional memories that will be attached to the material. The very act of teaching others will also activate different memory systems in Germaine: semantic memory from the practice and repetition, emotional memory from the act of presenting to his peers, episodic memory from the location and the people present, and emotional memory again as he receives feedback from his teacher and classmates. (pp. 120-121).
References
Association of Mathematics Teacher Educators. (2009). The mthematics TPACK (technological pedagogical content knowledge) framework. Retrieved from http://www.amte.net/AMTE_legacy/Math%20TPACK%20Framework.pdf
Battista, M. T., & Clements, D. H. (1995). Geometry and proof. Mathematics Teacher, 88(1), 48-54. Retrieved from http://investigations.terc.edu/library/bookpapers/geometryand_proof.cfm
Bennett, D. (2004). Exploring geometry with The Geometer’s Sketchpad. Berkley, CA: Key Curriculum Press.
Chazan, D., & Yerushalmy, M. (1998). Charting a course for secondary geometry. In R. Lehrer & D. Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 67-90). Mahwah, NJ: Lawrence Erlbaum Associates.
Christou, C., Mousoulides, N., Pittalis, M., & Pitta-Pantazi, D. (2004). Proofs through exploration in dynamic geometry environments. In M. J. Høines & A. B. Fuglestad (Eds.), Proceedings of the 28th conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 215-222). Retrieved from http://www.emis.de/proceedings/PME28/RR/RR194_Christou.pdf
Churches, A (2010). Bloom’s digital taxonomy. Retrieved from the Educational Origami wiki: http://edorigami.wikispaces.com/Bloom%27s+Digital+Taxonomy
Cirillo, M. (2009). Ten things to consider when teaching proof. Mathematics Teacher, 103(4), 250-257.
de Villiers, M. D. (1998). An alternative approach to proof in dynamic geometry. In R. Lehrer & D. Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 369-393). Mahwah, NJ: Lawrence Erlbaum Associates.
de Villiers, M. D. (2003). Rethinking proof with Geometer’s Sketchpad 4. Emeryville, CA: Key Curriculum Press.
Dreyfus, T. (1999). Why Johnny can’t prove. Educational Studies in Mathematics, 38(1), 85-109.
Edwards, M. T. (2008, October). Writing to learn: Enhancing students’ mathematical understanding through the creation of children’s storybooks. Grade 3-8 gallery workshop presented at the National Council of Teachers of Mathematics, Cleveland Regional Conference, Cleveland, OH.
Farrell, A. (1996). Roles and behaviors in technology-integrated precalculus classrooms. Journal of Mathematical Behavior, 15, 35-53.
Ferrance, E. (2000). Action research. Retrieved from Brown University’s The Education Alliance website: http://www.alliance.brown.edu/pubs/themes_ed/act_research.pdf
Fraser, R., Burkhardt, H., Coupland, J., Phillips, R. Pimm, D., & Ridgway, J. (1987). Learning activities and classroom roles with and without computers. The Journal of Mathematical Behavior, 6, 305-338.
Glass, B. J., & Deckert, W. (2001). Making better use of computer tools in geometry. Mathematics Teacher, 94(3), 224-229.
Goldenberg, E. P., & Cuoco, A. A. (1998). What is dynamic geometry? In R. Lehrer & D. Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 351-367). Mahwah NJ: Lawrence Erlbaum Associates.
Grandgenett, N., Harris, J., & Hofer, M. (2009, February). Mathematics learning activity types. Retrieved from College of William and Mary, School of Education, Learning Activity Types Wiki: http://activitytypes.wmwikis.net/file/view/MathLearningATs-Feb09.pdf
Heid, M. K., Sheets, C., & Matras, M. A. (1990). Computer-enhanced algebra: New roles and challenges for teachers and students. In T. J. Cooney (Ed.), Teaching and learning mathematics in the 1990’s (1990 NCTM yearbook; pp. 194-204). Reston, VA: National Council of Teachers of Mathematics.
Hollebrands, K., Laborde, C., & Sträßer, R. (2008). Technology and the learning of geometry at the secondary level. In K. Heid & G. W. Blume (Eds.), Research on teaching and the teaching and learning of mathematics: Vol. 1. Research synthesis (pp. 155-205). Charlotte, NC: Information Age Publishing.
Hoyles, C., & Healy L. (1999). Linking informal argumentation with formal proof through computer-integrated teaching experiments. In O. Zaslavsky (Ed.), Proceedings of the 23rd conference of the International Group for the Psychology of Mathematics Education. Retrieved from
http://www-didactique.imag.fr/preuve/Resumes/Hoyles/Hoyles99.html
Jackiw, N. (2006). The Geometer’s Sketchpad, Version 4.7. Berkley, CA: Key Curriculum Press.
Jones, K. (2000). Proving a foundation for deductive reasoning: Students’ interpretations when using dynamic geometry software and their evolving mathematical explanations. Educational Studies in Mathematics, 44, 55-85.
Knuth, E. (2002). Secondary school mathematics teachers’ conceptions of proof. Journal for Research in Mathematics Education, 33(5), 379-405.
Kosiak, J., & LeDocq, R. (2008). Connecting preservice teachers’ knowledge of mathematics, pedagogy and technology through learning object design. In K. McFerrin et al. (Eds.), Proceedings of Society for Information Technology and Teacher Education International Conference 2008 (pp. 5263-5270). Retrieved from http://www.editlib.org/p/28115.
Laborde, C. (2000). Dynamic geometry environments as a source of rich learning contexts for the complex activity of proving. Educational Studies in Mathematics, 44, 151-161.
Leijen, A., Lam, I., Wildschut, L., Simons, R., & Admiraal, W. (2009). Streaming video to enhance students’ reflection in dance education. Computers & Education, 52(1), 169-176.
Lester, M. L. (1996). The effects of The Geometer’s Sketchpad software on achievement of geometric knowledge of high school geometry students. Unpublished doctoral dissertation, University of San Francisco.
Marcos, E. (2008). Kids teaching kids. In K. McFerrin et al. (Eds.), Proceedings of Society for Information Technology and Teacher Education International Conference 2008 (pp. 4510-4514). Retrieved from http://www.editlib.org/p/27970.
Mariotti, M. A. (2000). Introduction to proof: The mediation of a dynamic software environment. Educational Studies in Mathematics, 44, 25-53.
National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (2001). Navigating through geometry in grades 9-12. Reston, VA: Author.
National Council of Teachers of Mathematics. (2006). Curriculum focal points for prekindergarten through grades 8 mathematics: A quest for coherence. Reston, VA: Author.
Senk, S. (1989). Van Hiele levels and achievement in writing geometry proofs. Journal for Research in Mathematics Education, 20(3), 309-321.
Sprenger, M. (2010). Brain based teaching in the digital age. Alexandria, VA: ASCD.
Webber, K. (2003). Students’ difficulties with proof (Research Sampler No. 8). Retrieved from the Mathematical Association of America website: http://www.maa.org/t_and_l/sampler/rs_8.html
Zbiek, R., & Hollebrands, K (2008). A research-informed view of the process of incorporating mathematics technology into classroom practice by in-service and prospective teachers. In K. Heid & G. W. Blume (Eds.), Research on teaching and the teaching and learning of mathematics: Vol. 1. Research synthesis (pp. 287-344). Charlotte, NC: Information Age Publishing.
Zevenbergen, R. (2001). Peer assessment of student constructed posters: Assessment alternatives in preservice mathematics education. Journal of Mathematics Teacher Education, 4, 95-113.
Author Notes:
The author would like to thank the reviewers and editors of the CITE journal for feedback on early drafts of this manuscript and colleagues Matthew Kennedy and LeAnn Neel-Romine for their guidance.
Kathryn G. Shafer
Ball State University
Email: [email protected]
Video 1 – http://kgshafer.iweb.bsu.edu/cite/shadowproof.swf
Video 2 – http://kgshafer.iweb.bsu.edu/cite/shadowmath.swf
Video 3 – http://kgshafer.iweb.bsu.edu/cite/sidesplitter.swf
Video 4 – http://kgshafer.iweb.bsu.edu/cite/disc_splitter.mp4
Video 5 – http://kgshafer.iweb.bsu.edu/cite/wallmirror.swf
Video 6 – http://kgshafer.iweb.bsu.edu/cite/disc_mirror.mp4
Video 7 – http://kgshafer.iweb.bsu.edu/cite/Geom_Voc_Proj_Lambda.mov
Video 8 – http://kgshafer.iweb.bsu.edu/cite/Geom_Voc_Proj_Theta.mov
Video 9 – http://kgshafer.iweb.bsu.edu/cite/Geom_Voc_Proj_Beta.mov
Video 10 – http://kgshafer.iweb.bsu.edu/cite/Geom_Voc_Proj_Alpha.mov
Problems Completed by Students From Exploring Geometry With The Geometer’s Sketchpad.
Problem | Student(s) |
| Burning Tent (page 40) Find the shortest distance from a point up river to the burning tent down river. | Adam and Dave |
| Feed and Water (page 42) Find the shortest distance between two points that routes the rider to a river and then a pasture. | Laura and Kayla |
| Height of the Telephone Pole (page 176) Find the height of a telephone pole using shadows. | Brittany and Diana |
| Height of a Flagpole (page 179) Find the height of a flagpole using reflection in a mirror. | Jackie and Lindsey |
| Side Splitter problem (page 181) Prove that if you intersect a triangle with a line parallel to one side, the remaining sides will be split proportionally. | Kourtney |
| Mirror on the Wall (page 41, Explore More) Find the length of a mirror necessary to reflect your entire image. | Casey and Jamie |
Height of a Flag Pole with a Mirror Problem
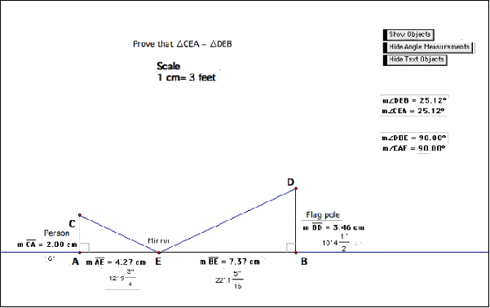
Last frame of Flag Pole Math video
http://kgshafer.iweb.bsu.edu/cite/flagpolemath.swf
Last frame of Flag Pole Proof video
http://kgshafer.iweb.bsu.edu/cite/flagpoleproof.swf
This problem incorporated the use of an actual mirror to find the height of a pole. The student team of Lindsey and Jackie produced their video in two parts, but there are two voices in the first video. Notice the use of fractions of an inch in this video, as the ladies used halves, fourths, and sixteenths in their conversion from Metric to Standard units. The students focused on three points of concern in our class discussion:
- The scale should use a colon instead of an equal sign.
- In both videos, the audio tracks state that “angles are perpendicular to the ground” instead of segments.
- Angle measurements are shown in the proof.
Students commented that this set of videos contained a nice use of screen space to display the computation and the proof.
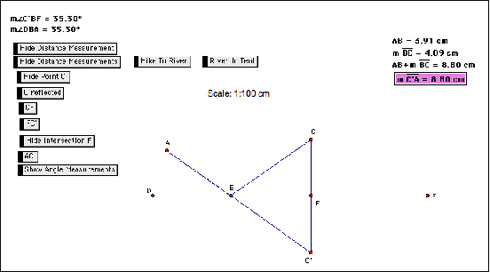
The Burning Tent Problem
 Last frame in the Burning Tent video
Last frame in the Burning Tent video
http://kgshafer.iweb.bsu.edu/cite/burningtent.swf
The task given in this problem was to find the shortest path from point A to the river (segment DE) to point C, which represents a tent that is on fire. Adam and David completed the burning tent problem with humor in the use of voices for different characters. In fact, it was impossible to not giggle when we viewed this as a class. Students also liked the animation of the points to illustrate the path of the runner. Upon viewing, students in our class noted the following corrections with this video.
- The scale is written as 1:100 cm and it should be 1 cm: 100 cm or 1:100.
- The actual distance from the starting point to the tent was not found.
- The proof is missing the step that states that the right angles are congruent.
I have used this problem repeatedly over the years and while it does seem a bit artificial, the students maintain the visual image in their heads of that silly burning tent (usually drawn with huge flames) and the reflection process necessary to create a proof.
The Feed and Water Problem
 Last frame in the Feed and Water video
Last frame in the Feed and Water video
http://kgshafer.iweb.bsu.edu/cite/feedandwater.swf
Laura and Kayla first located the shortest path from point D to the pasture, to the river, and to point E and then proved that it was indeed the shortest path. Students commented on the soothing nature of Laura’s voice but that maybe she went a bit too fast. A few corrections were noted in our class discussion:
- A ray should be named using two letters instead of just one.
- In the prove statement, segment FG should be segment GE.
- The scale factor is missing and actual distance was not found.
This video was truly a joint project, as I happened to be in the library when Laura and Kayla were completing the many takes necessary to produce their final version. The ladies noticed the reversal of the letters F and H in two locations on the audio track, but considering the time they had already spent in shooting the video it was left as is. When using software that does not allow for editing, I am also reluctant to fix minor errors due to time constraints.
![]()