In the Principles and Standards of School Mathematics the National Council of Teachers of Mathematics (NCTM) identified the “Technology Principle” as one of six principles of high quality mathematics education (NCTM, 2000). This principle states: “Technology is essential in teaching and learning mathematics; it influences the mathematics that is taught and enhances students’ learning” (p. 24). There is widespread agreement that mathematics teachers, not technological tools, are the key change agents to bringing about reform in mathematics teaching with technology (Kaput, 1992; NCTM 1991, 2000). Yet, preparing teachers to use technology appropriately is a complex task for teacher educators (Mergendoller, 1994). Waits and Demana (2000) argue that adoption of technology by teachers requires professional development that focuses on both conceptual and pedagogical issues, ongoing support in terms of “intensive start-up assistance and regular follow-up activities” and a desire to change from within the profession (p. 53). In addition, studies of teachers’ implementation of educational technology document that at least three to five years are needed for teachers to become competent and confident in teaching with technology (Dwyer, Ringstaff, & Sandholtz, 1991; Means & Olson, 1994).
The Curry Center for Technology and Teacher Education at the University of Virginia is developing materials to help preservice secondary mathematics, social studies, and science teachers (PSTs) learn to incorporate technology appropriately into their teaching. The focus of the mathematics team is to devise activities that will prepare secondary teachers to use technology to enhance and extend their students’ learning of mathematics. In this article we discuss the approach to developing and using materials for this purpose.
Use of Technology in Teacher Education
Technology is being incorporated into teacher education in numerous ways. Not surprisingly, there are different ways to categorize the various approaches taken by teacher educators to bring technology into their programs. One way to categorize these approaches is according to the primary user or controller of the technology—the teacher educator, the teacher, or the student. In some uses of technology in teacher education, the teacher educator is the primary user of the technology. For example, some teacher educators use multi-media case studies of rich teaching episodes to help PSTs analyze teaching and learning environments, and some use technology to present information or to demonstrate explorations. In many teacher education programs the teacher is being prepared to be the primary user of technology. For example, PSTs are being prepared to use technology productivity tools for word processing, grade and record keeping, web page production, and presentations. Also, many PSTs are using subject-specific software and websites to create presentations, lectures, lessons, and assessments. A third approach to incorporating technology in teacher education is to prepare PSTs to have their future students use technology to investigate concepts and solve meaningful problems in the content areas. For example, in the area of mathematics, PSTs are learning how to guide their students to use technologies such as spreadsheets, graphing calculators, dynamic geometry programs, and playable websites to explore mathematics concepts and use mathematics to solve problems in applied contexts.
The three uses of technology in teacher education presented above are connected with different purposes and all can lead to better teacher effectiveness and improved student learning. Thus, all are important. However, it has been our experience that the most direct and effective way to use technology to bring about enhanced student learning of mathematics is to prepare PSTs to incorporate into their teaching an array of activities that engage students in mathematical thinking facilitated by technological tools. Hence, in our preparation of secondary PSTs we emphasize the third use, in which ultimately the student is the primary user, and to some degree, the second use, in which the teacher is the primary user. Our materials reflect these emphases and thus are being developed around significant mathematical activities for school students.
In our classes, PSTs complete activities that, with some modification, are appropriate for secondary mathematics courses. We then use these completed activities to anchor class discussions of issues connected with secondary curriculum and instruction, national and state standards, sequencing of topics, the role of technology, and assessment. In the course of completing these activities, PSTs not only learn how to use the technology, but also how to incorporate technology into their teaching.
Guidelines for Technology-Based Activity Development
In the early phase of our work, we devised a set of guidelines to shape our development of mathematics activities and materials (Garofalo, Shockey, Harper, & Drier, 1999). The five guidelines below reflect what we believe to be appropriate uses of technology in mathematics teaching:
introduce technology in context
address worthwhile mathematics with appropriate pedagogy
take advantage of technology
connect mathematics topics
incorporate multiple representations
Each of these guidelines is discussed below and illustrated with one or more of our activities.
Introduce Technology in Context
Features of technology, whether mathematics-specific or more generic, should be introduced and illustrated in the context of meaningful content-based activities. Teaching a set of technology or software-based skills and then trying to find mathematical topics for which they might be useful is comparable to teaching a set of procedural mathematical skills and then giving a collection of “word problems” to solve using the procedures. Such an approach can obscure the purpose of learning and using technology, make mathematics appear as an afterthought, and lead to contrived activities. The use of technology in mathematics teaching is not for the purpose of teaching about technology, but for the purpose of enhancing mathematics teaching and learning with technology. Furthermore, in our experience, teachers who learn to use technology while exploring relevant mathematics topics are more likely to see its potential benefits and use it in their subsequent teaching. This guideline is in accord with the first recommendation of the President’s Committee of Advisors on Science and Technology, Panel on Educational Technology (1997): “Focus on learning with technology, not about technology” (p. 7).
Example: Simulating Freefall With Parametric Quadratic Equations
In this activity connecting quadratic equations and projectile motion, PSTs are introduced to the parametric graphing features of graphing calculators. PSTs are asked to derive an expression for the height of an object dropped from 500m above the surface of the Earth, as a function of time. They are then asked to construct a graph of this relationship, first with paper and pencil and then with graphing calculators. Our PSTs are able to derive a correct equation and generate a graph similar to those in Figure 1. (Click on the caption of the screenshot of the graph in the figure to see the graph being drawn.)
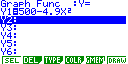
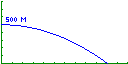
Figure 1. Casio 9850 Plus graphing calculator screenshots of freefall equation and graph
The graph in Figure 1 is appropriate, considering that the x -axis represents time and the y -axis represents the height of the object. However, many students often fail to fully attend to axis variables and sometimes interpret such a graph as a picture of the situation being represented. They interpret this graph as implying that the path of the object is outward and downward rather than as straight downward. Such a misinterpretation is referred to as an iconic interpretation (Kerslake, 1977; Leinhardt, Zaslavsky, & Stein, 1990) and is prevalent with secondary school students. We challenge our PSTs to generate a graph that simulates the actual path of a freefalling object. This involves use of parametric equations, which all of our PSTs have studied in calculus, but most have forgotten or have not considered for high school use. Rather than teach PSTs to use the graphing calculator parametric features ahead of time and apply here, we introduce these features in this context, where PSTs can see its direct applicability and usefulness. Figure 2 shows the parametric equation and graph that simulates the object’s path. (Click on the caption of the graph screenshot in the figure to see the graph being drawn.)
Figure 2. Calculator screenshots of parametric freefall equation and graph
PSTs then compare and contrast the graphs. Subsequently, we use the graphs as springboards to discuss various aspects of visual representations (e.g., connected versus plot graphing), iconic misrepresentations, incorporation of parametric equations in the curriulum, and use of parametric equations to enrich the treatment of other school mathematics topics. PSTs then apply these features to tasks involving horizontal motion and angular projectile motion.
Address Worthwhile Mathematics with Appropriate Pedagogy
Content-based activities using technology should address worthwhile mathematics concepts, procedures, and strategies, and should reflect the nature and spirit of mathematics. Activities should support sound mathematical curricular goals and should not be developed merely because technology makes them possible. Indeed, the use of technology in mathematics teaching should support and facilitate conceptual development, exploration, reasoning and problem solving, as described by the NCTM (1989, 1991, 2000).
Technology should not be used to carry out procedures without appropriate mathematical and technological understanding (e.g., inserting rote formulas into a spreadsheet to demonstrate population growth). Nor should it be used in ways that can distract from the underlying mathematics (e.g., adding so many bells and whistles into a Power Point slideshow that the mathematics gets lost). In other words, mathematical content and pedagogy should not be compromised.
Another way to prevent technology use from compromising mathematics is to encourage users to connect their experiential findings to more formal aspects of mathematics. For example, students using software to explore geometric shapes and relationships should be asked to use previously proved theorems to validate their empirical results, or use their new findings to propose new conjectures. Mathematical notions of “proof ” and “rigor” need to be addressed as well. In other words, technology should not influence students to take things at face value or to become what Schoenfeld (1985) referred to as “naïve empiricists.” This guideline is in accord with the second recommendation of the President’s Committee of Advisors on Science and Technology, Panel on Educational Technology (1997): “Emphasize content and pedagogy, and not just hardware” (p. 7).
Example: Exploring the Pythagorean Theorem
On way we explore issues regarding appropriate pedagogy with technology with our PSTs is with the following activity. The emphasis of the activity is more on the principles of teaching the mathematics than on the mathematics itself. PSTs discuss how this topic is traditionally taught to students, as a rote memorization of a 2 + b 2 = c 2 without any conceptual understanding that a 2 , b 2 and c 2 represent areas of squares with sides length a , b , and c . We then discuss how technology could be used to enhance the students’ understanding of the theorem, and guide them through a model lesson of how the Pythagorean theorem could be taught using The Geometer’s Sketchpad (Jackiw, 1997).
PSTs are first asked to use the Sketchpad to construct a right triangle, measure each side, and numerically confirm the a 2 + b 2 = c 2 relationship. They then learn how to use Sketchpad features to script a construction of a square. Next the PSTs play back their scripts to place a square on each of the sides of the right triangle and add measurements to create a construction similar to the one in Figure 3. The dynamic Sketchpad environment allows the PSTs to drag the triangle’s vertices or sides to manipulate the construction, keeping the characteristics of the geometric figures intact. As the construction changes, the sum of the area of the squares on the legs of the right triangle always remain equal to the area of the square on the hypotenuse of the right triangle. (Click on Figure 3 caption to see an animation of this construction.)
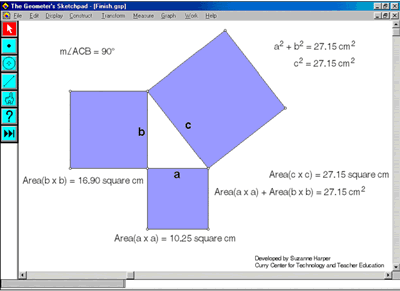
Figure 3. Sketchpad file of the Pythagorean theorem
PSTs then discuss connections between the different representations of the Pythagorean Theorem, advantages of each representation in teaching this topic, and benefits of using the Sketchpad to create and manipulate the constructions. This activity illustrates a point made in the Technology Principle of the NCTM Principles and Standards : “Technology also provides a focus as students discuss with one another and with their teacher the objects on the screen and the effects of the various dynamic transformations that technology allows (NCTM, 2000, p. 24).”
We typically pose the following question to our PSTs: Does the manipulation of this construction constitute a mathematical proof of the Pythagorean theorem? One semester we received four types of responses: “I think it’s a proof;” “I don’t know if this is a proof;” “I hope it’s a proof;” and “Of course this is not a proof!” These responses gave us the perfect opportunity to discuss the notion of an “informal” geometry proof, the role of technology in an informal proof, and the necessity of a formal proof. It is important for PSTs to engage in such discussions since they will be helping their future students “select and use various types of reasoning and methods of proof” (NCTM, 2000, p. 342). Subsequently, we investigate other dynamic constructions of geometric representations of the Pythagorean theorem and associated formal proofs to help PSTs see other representations of the mathematical structure of the Pythagorean theorem.
Take Advantage of Technology
Activities should take advantage of the capabilities of technology, and hence should extend beyond or significantly enhance what could be done without technology. Technology enables users to explore topics in more depth (e.g., interconnect mathematics topics, write programs, devise multiple proofs and solutions) and in more interactive ways (e.g., simulations, data collection with probes). Technology also makes accessible the study of mathematics topics that were previously impractical, such as recursion and regression, by removing computational constraints.
Using technology to teach the same mathematical topics in fundamentally the same ways that could be taught without technology does not strengthen students’ learning of mathematics and belies the usefulness of technology. Furthermore, using technology to perform tasks that are just as easily or even better carried out without technology may actually be a hindrance to learning. Such uses of technology may convince teachers and administrators that preparing teachers to use technology is not worth the considerable effort and expense necessary to do so.
This guideline supports the Technology Principle of the NCTM Principles and Standards for School Mathematics . “Teachers should use technology to enhance their students learning opportunities by selecting or creating mathematical tasks that take advantage of what technology can do efficiently and well—graphing, visualizing, and computing” (NCTM, 2000, p. 25).
Example: Exploring Sierpinski Polygons
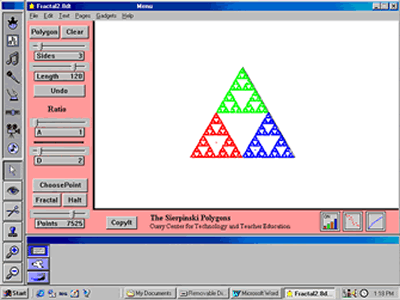
The following activity introduces our PSTs to Sierpinski Triangles and related fractals . Sierpinski’s Triangle, first introduced by Waclaw Sierpinski in 1916, can be constructed in several ways. One way is to start with an equilateral triangle and a randomly chosen point inside, on, or outside the triangle. Next, randomly choose a vertex of the triangle and place a new point half way between the initial point and the randomly chosen vertex. Then, again randomly choose a vertex of the triangle and place a third point half way between the second point and the randomly chosen vertex. The triangle is constructed by continuing this recursive process, that is, by randomly choosing a vertex of the triangle and placing a point half way between that vertex and the previous point.
We ask our PSTs to construct a Sierpinski Triangle of 20 points using a triangle template and tossing one die to randomly determine vertices, observe their results, and predict what the triangle would look like if they were able to continue the process for a total of 5,000 points. Clearly, plotting 5,000 points is impractical to do by hand, so we developed our Sierpinski Polygon program in MicroWorlds (Logo Computer Systems, Inc., 1997) to carry out this process. Figure 4 shows Sierpinski’s triangle constructed with 7,525 points. (Click on the figure caption to see an animation of the construction.
Figure 4. Sierpinski’s Triangle
We ask our PSTs to analyze this triangle and comment on their observations. Next, we ask them to make predictions about and use the program to investigate various “What if” questions (e.g., What if we started with a hexagon? What if we used a ratio of one third instead of one-half? What if we used ratios greater than one?). They then explore various shapes and ratios, and determine the ratio, as a function of the number of sides of a polygon, which gives the “best” Sierpinski polygon. Figure 5 shows a triangle constructed with a ratio of 1.5. (Click on the figure caption to see an animation of the construction.
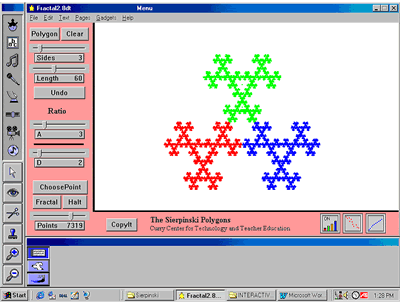
Figure 5. Sierpinski Triangle with r = 1.5
We use this Sierpinski activity as a springboard to engage PSTs in mathematical discussions of constrained randomness, “best” polygons, and fractals and self-similarity. Our pedagogical discussions focus on the role of fractal geometry in the mathematics curriculum, how this activity connects to local and national curriculum standards, connections between aesthetics and mathematics, and the usefulness and place of “What if” questions in mathematics instruction to help students appreciate how mathematicians advance their discipline.
Connect Mathematics Topics
Technology-augmented activities should facilitate mathematical connections in two ways: (a) interconnect mathematics topics and (b) connect mathematics to real-world phenomena. Technology “blurs some of the artificial separations among some topics in algebra, geometry and data analysis by allowing students to use ideas from one area of mathematics to better understand another area of mathematics” (NCTM, 2000, p. 26). Many school mathematics topics can be used to model and resolve situations arising in the physical, biological, environmental, social, and managerial sciences. Many mathematics topics can be connected to the arts and humanities as well. Appropriate use of technology can facilitate such applications by providing ready access to real data and information, by making the inclusion of mathematics topics useful for applications more practical (e.g., regression and recursion), and by making it easier for teachers and students to bring together multiple representations of mathematics topics. This guideline supports the curriculum standards of the NCTM (1989, 2000).
Example: Connecting Infinite Series and Geometric Constructions
The Curriculum and Evaluation Standards for School Mathematics (NCTM, 1989) stated, “The interplay between geometry and algebra strengthens students’ abilities to formulate and analyze problems from situations both with in and outside mathematics” (p. 161). One way students can investigate the connections between geometric and algebraic representations is with infinite series. In this activity, PSTs explore connections between convergent infinite geometric series and recursive processes of subdividing regular polygonal regions. These recursive processes result in the construction of Baravelle Spirals. In this context PSTs learn to construct recursive scripts with the Sketchpad. Figure 6 illustrates the recursive process of (a) constructing the midpoints of the sides of an innermost equilateral triangle, (b) connecting these midpoints to generate four small congruent equilateral triangles (each one fourth the area of the larger triangle), and (c) coloring a sequence of successively smaller triangles in a clockwise rotation. PSTs use this process to visualize and subsequently prove that:
![]()
(Click on the Figure 6 caption to see an animation of this construction.)
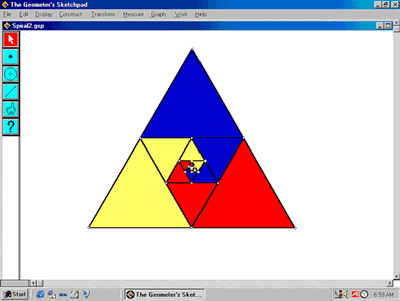
Figure 6. Sketchpad sketch of a Baravelle spiral generated from an equilateral triangle
PSTs explore infinite series by computing several partial sums initially and then following with more formal calculations based on mathematical limits. They discuss the role and advantages of geometric representations, instructional strategies for teaching infinite series, partial sums and convergent series, and how this activity connects to both state and national algebra and geometry standards.
Example: Connect Mathematics With Social Studies
To illustrate how technology can facilitate connections between mathematics and other disciplines we present our PSTs with the following information from a story in our local newspaper:
On Sunday, March 12, 2000 the Charlottesville Daily Progress contained an article reporting the results of a Washington Post-ABC News Poll. The article reported “Gore leads Bush by 48 percent to 45 percent, a statistical tie.” It also reported, “A total of 1,218 adults, including 999 self-described registered voters, were interviewed” and the “margin of error for the overall results is plus or minus 3 percentage points, and slightly larger for results based on only the registered voters.”
We ask PSTs to interpret, in their own words, what is meant by a “margin of error of plus or minus 3 percentage points” and what is meant by “a statistical tie.” They are then asked to discuss the appropriate statistical test for such a poll, assess the accuracy of the newspapers’ reporting, and comment on the appropriateness of the sample size. Using their graphing calculators, PSTs check the numbers in the article, run similar numbers for several different sample sizes, and make informed comments about the questions presented to them. Figure 9 shows that the newspaper reporting was accurate, with a confidence interval ranging from approximately .45 to .51 (.48 ± .03).

Figure 7. 95% Confidence Interval for p = .48.
Next we suggest they consider the algebraic representation of the standard error s as a function of sample size n , s ( n )= Ö ( p (1- p )/ n ), and graph this relationship for this particular sample proportion (p = .48) and confidence interval (.95) on their graphing calculators. By tracing the graph they observe numerically the margins of error ( y -coordinate) associated with various sample sizes ( x -coordinate). Furthermore, they see from the graphical representation that there is a point of diminishing returns. The animation below shows the margins of error for sample sizes of 100, 500 and 1000. (Click on the Figure 8 caption to view the animation.)

Figure 8. Graph of the 95% Standard Error.
The PSTs then discuss the trade-offs involved with various sample sizes and determine reasonable samples for presidential and other polls (e.g., Does it make sense to poll a sample of 10,000?).
Initially, many PSTs struggle with the above questions, even though they have recently studied the underlying statistical ideas (e.g., sampling distribution and confidence interval) in mathematical statistics courses. They often fail to connect the abstract mathematics they are learning in class with real-world uses. This presents us with a “pedagogical moment” —a time to discuss why they were able to operate successfully with these concepts in a mathematics class, yet struggle with applying them outside of class. Our PSTs then analyze and discuss why their mathematics education did not prepare them to apply mathematics concepts to real situations and devise instructional experiences to help their students to see how mathematics is connected to other disciplines.
Other class discussions center around how such an activity is consistent with state and national mathematics standards, how such activities should be sequenced in a unit on confidence intervals, and what value the technology has in such an activity. PSTs see that the technology facilitates this exploration by reducing the effort and time associated with performing repeated calculations and graphing and, thus, frees students to observe and analyze results and patterns. The Technology Principle of the NCTM Principles and Standards for School Mathematics emphasizes this point: “The computational capacities of technological tools extends the ranges of problems accessible to students and also enables them to execute routine procedures quickly and accurately, thus allowing more time for conceptualization and modeling” (NCTM, 2000, p. 24).
Incorporate Multiple Representations
Activities should incorporate multiple representations of mathematical topics. Research shows that many students have difficulty connecting the verbal, graphical, numerical and algebraic representations of mathematical functions (Goldenberg, 1988; Leinhardt et al., 1990). Appropriate use of technology can be effective in helping students make such connections (e.g., connecting tabulated data to graphs and curves of best fit, generating sequences and series numerically, algebraically, and geometrically). “We, as mathematics educators, should make the best use of multiple representations, especially those enhanced by the use of technology, encourage and help our students to apply multiple approaches to mathematical problem solving and engage them in creative thinking” (Jiang & McClintock, 2000, p.19).
Example: Exploring Maximum Area
An example of using technology to explore multiple representations involves a popular problem in which students find the maximum area for a rectangular pigpen given a fixed amount of fencing. To begin the investigation in our methods course, PSTs are given a handful of square tiles (1″ x 1″), asked to build all possible rectangular pigpens with a perimeter of 24 inches, record the dimensions and resulting area, and verbalize a possible relationship. As the PSTs note, the maximum area (36 in 2 ) is obtained with a 6″x 6″ pigpen. We then pose the question: “With any given perimeter, does a square pigpen always provide the maximum area?”
The spreadsheet in Figure 9 allows students to explore this question by systematically varying the length of side X for a fixed perimeter and observing the subsequent numerical, geometrical, and graphical representations. The PSTs also change the value of the perimeter and then vary X to find the associated maximum. Through repeated experimentation within this Microsoft Excel (Microsoft, 2000) environment, PSTs recognize that the value of the parameter X resulting in the maximum area of the rectangle is one fourth of the given perimeter P (e.g., P = 60, X = 15: P = 100, X = 25). PSTs can extend this problem through calculus by using algebraic formulas for perimeter and area, symbolic manipulation, and the first derivative of the equation Area = X ( P- 2 X )/2 with respect to X . (Click on the Figure 9 caption to see an animation of this exploration.)
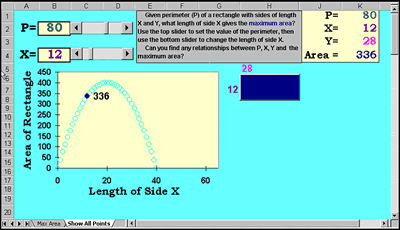
Figure 9. Linked multiple representations of the maximum area problem.
The common “pigpen” problem allows PSTs to investigate and deepen their understanding of the relationship between perimeter and area with a multitude of representations. They begin with a manipulative geometric exploration, tabular recordings and a verbal description of the relationship. They then move to a digital environment with numerical , graphical , and geometrical representations and finally use a paper-and-pencil algebraic representation and symbolic manipulations to confirm the relationship. This investigation is used to prompt discussions with PSTs about (a) the benefits and drawbacks of using multiple representations, including manipulatives, in understanding mathematical relationships and (b) the importance of connecting mathematical topics from middle school through calculus.
Illustrations in Action
Our five guidelines are not independent of one another. All the examples given within each of the guidelines above also illustrate one or more of the other guidelines. The examples used were intended to provide quick illustrations highlighting a particular guideline. A more in-depth look at two illustrations in action will highlight the interconnectedness of the guidelines and provide examples of rich investigations in our secondary methods course.
Illustration in Action 1: Linear Relationships and Regression
The study of linear functions has been a mainstay and an important building block in secondary school mathematics. The advent of powerful technology tools has extended the study of linear functions to include a data-analysis technique called linear regression, in which data points clustering in a linear fashion on a scatterplot can be “best fit” by a line to describe the relationship between the two variables. The most commonly used technique, least-squares regression, can be quickly performed on graphing calculators, computer graphing software, and standard spreadsheets. Although technology places this computationally intense topic within the reach of all students (Vonder Embse, 1997), it is important that PSTs and their future students have a conceptual understanding of what it means to perform a least-square regression on data points and how to interpret the results.
We use the following activity to introduce students to linear regression in the context of examining a data set on smoking and lung cancer. We first give the PSTs the data set and ask them to do a qualitative analysis and conjecture a relationship between the two variables. Because this data is clustered by occupational groups, PSTs can discuss a variety of social and environmental factors that could affect either variable (e.g., professionals tend to have a low smoking rate, furnace and mill workers have the highest rate of death from lung cancer). One conjecture that PSTs make is that, as the rate for smoking increases, the rate for death from lung cancer also seems to increase. To help analyze this conjecture, the PSTs learn how to sort data in ascending order and create scatterplots in a spreadsheet. This allows them to see trends and examples of data that are contrary to the conjectured trend. The PSTs learn how to change the scale on the axes to represent the data in favorable and unfavorable ways for the tobacco industry and discuss the implications from each representation. (See Figure 10.)
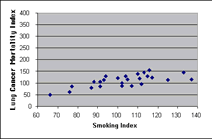
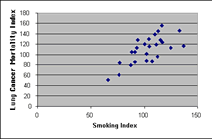
Figure 10. Data displayed (a) favorable and (b) unfavorable for the tobacco industry.
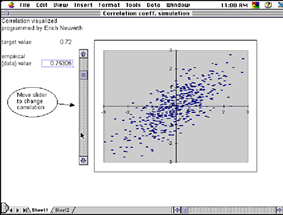
The focus of the lesson then turns to comparing their analyses with each representation (table and graph) and mathematically describing a possible relationship between the variables. Questions about the “strength” of relationship lead into a discussion about the Pearson product-moment correlation coefficient ( r ), which gives a mathematical index of the strength of the relationship between two variables. Having secondary students understand the correlation coefficient poses “a dilemma, unknown a generation ago, for mathematics teachers” (Coes, 1995, p. 758). Instead of rotely memorizing the meaning of r , we have our PSTs use the Correlation Visualized spreadsheet (Neuwirth, 1995) shown in Figure 11 to construct their own interpretation of the values of r, and discuss how they could use this visualization to help their students understand the meaning of a correlation coefficient. (Click on the Figure 11 caption to view an animation of the changes in the scatterplot.)
Figure 11. The Correlation Visualized spreadsheet
The PSTs use the Correlation Visualized spreadsheet to estimate the value of r for the smoking and lung cancer data and then use the Excel function CORREL( y range, x range) to calculate the exact value of r . We discuss how to interpret the value ( r = 0.71) in terms of the data and using the square of the correlation coefficient ( r 2 = 0.49) to describe the proportion of variance in one variable (smoking) that is associated with the variance in the other variable (death from lung cancer). With a moderately strong value for r , it is reasonable to consider predictive questions such as “If an occupational group has a smoking index of 120, what would you predict their mortality index to be?” The question of prediction encourages the PSTs to use the numerical and graphical representations of data to make an estimate for the predicted mortality index and leads to a discussion of using a line to approximate the relationship and facilitate the prediction process. After using the drawing tools to place an estimated line of best fit on the scatterplot and using algebraic techniques to determine an equation for the line, the PSTs learn how to add a linear regression trendline to a scatterplot in Excel . (See Figure 12). The PSTs then compare their estimated line and equation with the ones calculated through Excel , and compare the predictions made from both techniques.
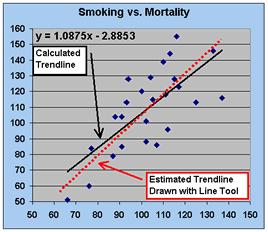
Figure 12. Scatterplot including estimated and calculated linear trendlines
The comparison of the PSTs’ estimated line and the one calculated through Excel prompts an investigation into why the calculated line is the “best.” We have the PSTs use a multimedia activity from the ExploreMath.com website to investigate how to minimize the sum of the squared error (numerically and geometrically) in fitting a line to a set of data points. The website includes linked algebraic, numeric, and graphic representations that can change dynamically through direct manipulation with all of the representations. The visualization of the squared error represented geometrically is a powerful tool in facilitating conceptual understanding of the least-squares regression model. (Click on the Figure 13 caption to see an animation of the activity.)
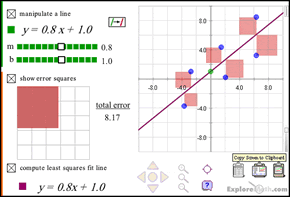
Figure 13. ExploreMath file illustrating a least-squares linear regression line
This investigation of the relationship between smoking and lung cancer also includes discussions about residuals and the effect of outliers on the linear regression equation. The PSTs learn many mathematics concepts and technology skills and engage in meaningful discourse about their own learning in this activity and the pedagogical issues surrounding teaching these topics and using the technology to effectively promote conceptual understanding, rather than mindless “speedy” calculations.
This “illustration-in-action” is rich in mathematics and pedagogy discussions and uses a variety of technology tools to facilitate the teaching and learning process. The PSTs learn how to use the technology tools in the context of the investigation, when the needed technology skill is appropriate (e.g., adding a trendline to a scatterplot). By focusing on conceptual understanding of both correlation coefficient and least-squares regression, we are modeling appropriate pedagogy and sound mathematical practices. We take advantage of technology as a vehicle for both procedural and conceptual understanding through using multiple representations, as well as facilitating classroom discussions. In addition, the mathematics is connected to a real-world controversial issue and also connects the study of linear functions in algebra to statistical techniques of linear regression.
Illustration in Action 2: Trigonometric Graphs
The study of trigonometry, which translates verbatim as “triangle measurement,” began more than 2,000 years ago, partially as a means to solving land surveying problems. Traditionally, trigonometry is introduced as the ratios of the lengths of sides of a right triangle. This is commonly the first time the students hear the “SOH-CAH-TOA” acronym to remember the three common trigonometric ratios:
![]()
![]()
![]()
Because most students are not introduced to these ratios as functions of angle measurement until precalculus courses, the connections between the “right triangle” trigonometry and the graphs of functions of sine, cosine and tangent are not apparent. The following description is an illustration of an activity we use in our secondary methods class to connect right triangle and functional representations of trigonometry.
Using The Geometer’s Sketchpad , PSTs construct a unit circle centered at the origin. We ask them to investigate a group of right triangles where: (a) the length of the hypotenuse is equal to the radius of the circle, (b) the vertex of the right angle is confined to the x-axis, and (c) a vertex is at the origin. Working in pairs, the PSTs construct a right triangle that satisfies these three conditions, comparing their sketch to the one in Figure 14.
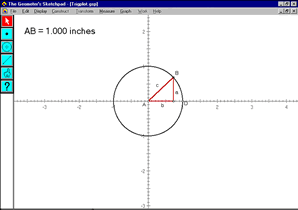
Figure 14. Constructed right triangle with reference < DAB
Our PSTs drag point B around the circle and focus their attention on the lengths of sides a and b . They record qualitative descriptions of the lengths of sides a and b, as point B is dragged around the circle. As they discover, it is difficult to describe specifics about lengths a and b without being able to pinpoint locations around the unit circle. Introducing the measurement of angle DAB helps them describe where point B is located on the circle. One point of conflict arises when the PSTs observe that The Geometer’s Sketchpad displays angle measurement as a number between -180° and 180°, rather than between 0° and 360°, to which they are accustomed. We discuss the possible conceptual and instructional problems that could arise in a high school classroom from this aspect of the technology. The PSTs then drag point B around the circle to find the maximum and minimum lengths of sides a and b .
In their sketches, the PSTs notice the lengths of the sides of the triangle changing as point B is dragged around the circle and devise a plan to graph the length of side a versus the measure of angle DAB geometrically . Once they finish the construction, we have the PSTs predict the shape of the graph on paper before activating their sketch (See Figure 15), and then reconcile any differences between their predicted graph and the graph sketched by the Sketchpad . (Click on the Figure 15 caption to activate the sketch.)
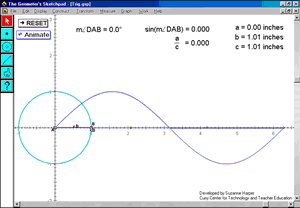
Figure 15. Sketchpad file of a geometric construction of the sine function
As an in-class exercise or for homework, we have the PSTs construct a graph of the length of side b versus the measure of angle DAB to illustrate the graph of the cosine function. This geometric construction is similar to the previous construction; however it is more challenging. Once the PSTs successfully construct the graph of side b versus the measure of angle DAB , we qualitatively and quantitatively compare and contrast the sine and cosine functions using a sketch similar to Figure 16. This investigation of the relationship between the right triangle and functional representations of trigonometry extend to activities challenging the PSTs to develop a geometric plan to construct the graphs of the other four trigonometric functions using the Sketchpad .
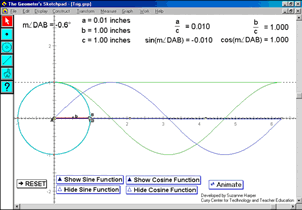
Figure 16. Sketchpad file of a geometric construction of the sine and cosine functions
PSTs follow these constructions with discussions of the various representations of trigonometric functions and how they relate to secondary students’ conceptions and misconceptions. They then discuss how such constructions can be integrated into instruction. Subsequently, we continue our investigation of trigonometric functions with a graphing calculator activity that illustrates how technology facilitates use of mathematics to model real-world phenomena, in this case connecting trigonometry to physical geography. Together, these activities provide opportunities for the PSTs to view “mathematical ideas from multiple perspectives” (NCTM, 2000, p.24).
The PSTs examine the average monthly temperature data given in Table 1 and describe and interpret patterns in the data over one year.
Table 1
Average Monthly Temperatures
Apr May Jun Jul Aug Sep Oct Nov Dec Jan Feb Mar Apr Wash. DC 54 64 73 77 75 68 57 46 37 34 36 45 54 Verhoyansk 5 32 54 57 48 36 5 -35 -53 -57 -48 -25 5 Buenos Aries 63 55 48 50 52 55 59 66 72 73 73 70 63
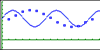
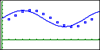
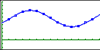
Next, they plot the data on their graphing calculators and compare the shape of their scatterplots with their descriptions and interpretations. We discuss mathematical models of the data and the general form of the sine function, y = A sin( B ( x + C ))+ D . We ask our PSTs to determine a “best fit” sine curve for the Washington data incrementally , by determining one coefficient at a time and graphing the resulting curves. Click on the Figure 17 caption to see an animation of an incremental curve fit that first adjusts the amplitude ( A ), then the vertical shift ( D ), then the period ( B ), and finally the horizontal shift ( C).
Figure 17. Incremental curve fitting
Our PSTs next discuss the fit of this curve and then compare it with the least squares sine regression equation determined by using the graphing calculator feature. (See Figure 18.)
Figure 18. Calculator screenshot of the calculation of a sine regression
PSTs are then able to estimate from the scatterplots the coefficients for the Verhoyansk and Buenos Aires data and later verify their estimates. We then discuss the relationships between the coefficients for the best-fit equations for the three cities, and the geographical locations of these cities (e.g., latitude, proximity to an ocean). We discuss advantages of the various forms of representation and how they should be connected in secondary mathematics instruction.
PSTs are often “rusty” with trigonometric equations, and from this activity they develop better understandings of the effect of each of the coefficients on the graph of the sine function. We discuss the teaching of this topic and how real-world phenomena can be incorporated into instruction. This is followed by investigations of periodicity in other contexts. For example, we use calculator-based probes to collect and display data from physical experiments (e.g., a light intensity probe to investigate cycles per second with florescent lights and an amplifier to investigate cycles per second of notes generated by tuning forks).
This “illustration-in-action” solidifies what we believe to be an appropriate use of technology in mathematics teaching. The PSTs learn how to use the technology tools (e.g., the trace , animation and movement features of Sketchpad) in the context of the investigation. Focusing on relationships between the right triangle and functional representations of trigonometric functions demonstrates worthwhile mathematics with appropriate pedagogy . Furthermore, this activity takes advantage of technology to connect trigonometric topics traditionally taught in geometry to those addressed in the pre-calculus curriculum, and connect trigonometry to another discipline, in each case using multiple representations of trigonometric relationships.
Conclusion
The preparation of secondary mathematics teachers who are able to use technology to enhance students’ learning of mathematics is not a trivial matter. PSTs need to develop technology skills, enhance and extend their knowledge of mathematics with technological tools, and become critical developers and users of technology-enabled pedagogy. The creation of guidelines and materials represents a starting point in our efforts to prepare PSTs to use technology appropriately
We believe that our guidelines for the use of technology in mathematics teaching reflect the views of most mathematics educators and that our materials have the potential to provide mathematics educators with concrete starting places for integrating meaningful technology activities in their teacher education programs. Internal and external field-testing of our materials indicate that mathematics educators have found the activities useful in mathematics content courses, mathematics methods courses, and courses designed specifically on technology and mathematics education. However, we are now striving to create models for best using such materials in teacher education programs to help PSTs use technology to enhance their students’ learning of mathematics.
We invite readers to access all of our graphing calculator, Excel , Geometer’s Sketchpad , and MicroWorlds materials at the Curry Center for Technology and Teacher Education mathematics web site. We encourage you to use our activities in your courses for preservice and inservice mathematics teachers and send us your feedback and suggestions.
References
Coes, L., III. (1995). What is the r for? The Mathematics Teacher, 88 (9), 758-761, 768-769.
Dwyer, D.C., Ringstaff, C., & Sandholtz, J.H. (1991). Changes in teachers’ beliefs andpractices in technology-rich classrooms. Educational Leadership, 48 (8), 45-52.
ExploreMath.com (2000). Least Squares Regression . http://www.exploremath.com/activities/Activity_page.cfm?ActivityID=6
Garofalo, J., Shockey, T., Harper, S., & Drier, H. (1999). The Impact project at Virginia: Promoting appropriate uses of technology in mathematics teaching. Virginia Mathematics Teacher , 25 (2), 14-15.
Goldenberg, E.P. (1988). Mathematics, metaphors, and human factors: Mathematical, technical, and pedagogical challenges in the educational use of graphical representations. Journal of Mathematical Behavior , 7 , 135-173.
Jackiw, N. (1997). The Geometer’s Sketchpad , Version 3.1 . Berkeley, CA: Key Curriculum Press.
Jiang, Z., & McClintock, E. (2000). Multiple approaches to problem solving and the use of technology. Journal of Computers in Mathematics and Science Teaching, 19 (1), 7-20.
Kaput, J.J. (1992). Technology and mathematics education. In D.A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 515-556) . New York:Macmillan.
Kerslake, D. (1977). The understanding of graphs. Mathematics in School, 6 (2), 56-63.
Leinhardt, G., Zaslavsky, O., & Stein, M.K. (1990). Functions, graphs, and graphing: Tasks, learning and teaching. Review of Educational Research , 60 (1), 1-64.
Logo Computer Systems Inc. (1997). MicroWorlds, Version 2.0 . Montreal, CA: Author.
Means, B., & Olson., K. (1994). Tomorrow’s schools: Technology and reform in partnership. In B. Means (Ed.), Technology and the education reform (pp. 191-222). San Francisco: Jossey-Bass.
Mergendoller, J.R. (1994). The Curry School of Education, University of Virginia. In Exemplary approaches to training teachers to use technology, vol. 1: Case studies (pp. 4.1-4.24). Novato, CA: Beryl Buck Institute for Education.
Microsoft Corporation (2000). Microsoft Excel 2000 . Redmond, WA: Author.
National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics . Reston, VA: Author.
National Council of Teachers of Mathematics. (1991). Professional standards for teaching mathematics . Reston, VA: Author.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
Neuwirth, E. (1995). Correlation visualized . http://sunsite.univie.ac.at/Spreadsite/statexamp.
President’s Committee of Advisors on Science and Technology, Panel on Educational Technology. (1997). Report to the President on the use of technology to strengthen K-12 education in the United States .
Schoenfeld, A. (1985). Mathematical problem solving. New York: Academic Press.
Waits, B.K., & Demana, F. (2000). Calculators in mathematics teaching and learning: Past, present, and future. In M. J. Burke and F. R. Curcio (Eds.), Learning mathematics for a new century (pp. 51-66). Reston, VA: National Council of Teachers of Mathematics.
Vonder Embse, C. (1997). Visualizing least-square lines of best fit. The Mathematics Teacher, 90 (5), 404-408.
Contact Information
Joe Garofalo
Curry School of Education
University of Virginia
Lambeth House
1912 Thompson Road
Charlottesville, VA 22903
[email protected]
![]()


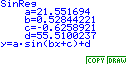
Related Articles