Economies and societies are rapidly shifting to capitalize and focus on technology. Within K-12 education, technology has played an important role both as a medium to teach a variety of curricular materials and as an end in itself, by teaching computer science and engineering concepts, so that students today will be able to make informed decisions about computation and technology issues of global importance in the future.
When considering technology as a medium, computer-based games are a good example. Games have been growing in popularity as an avenue for learning STEM, and a growing body of research has shown the effectiveness and impact of playing games as a way to learn and practice curricular content (Habgood & Ainsworth, 2011; Lester et al., 2013; Steinkuehler et al., 2012). Educational games foster engagement and motivation among students while enhancing learning and promoting teamwork (Devlin, 2011). Such evidence suggests that games provide benefits to students above and beyond learning that could serve as effective, alternative activities for learning in science, technology, engineering, and mathematics (STEM) classrooms.
When considering technology as an end, an important concept at the K-12 level is computational thinking (CT), a set of skills that involves solving problems, designing systems, and understanding human behavior by drawing on the concepts fundamental to computer science (Wing, 2006). CT has been called a universally applicable set of attitudes and skills that everyone, not only computer scientists, would be eager to learn and use and a vital ingredient of STEM learning.
Educators and business leaders have recognized that computational thinking, including problem solving, systems thinking, computational modeling, and data practices (Weintrop et al., 2016), is a new basic skill necessary for economic opportunity and social mobility and is used in most fields. Students should have the opportunity to learn CT in school and be prepared with skills they can apply in almost every discipline (Guzdial, 2008).
The reality is, however, that educators have found changing their practices to incorporate technology as a medium to be challenging, and it has been even harder for STEM educators to understand how to integrate technology as an end, such as integrating CT concepts into their curricula. Teachers lack experience and training to teach CT, which has made it hard to find ways to blend this curriculum in STEM classrooms. A literature review (Lockwood & Mooney, 2017) concluded that more detailed lesson plans and curriculum on CT would benefit teachers by providing guides on how to feasibly incorporate CT in their own classrooms.
Although many differences exist between mathematics and computer science, mathematics teachers are natural candidates for teaching computational thinking. Mathematics teachers are already prepared in problem solving, precision, and the rigor required in a software creation process, and the National Research Council has highlighted how mathematics and computational sciences depend on each other: software engineers apply the mathematical form of scientific theories, while mathematicians and scientists use powerful information technologies created by software engineers. Engineers and mathematicians can thereby accomplish analyses, investigations, and models that might otherwise be out of the question without each other (National Research Council, 2012, p. 65). With the training and experience of mathematics teachers, this relationship between mathematics and computational sciences should also be considered in K-12 classrooms.
This project addresses the growing need of teacher professional development in technology integration in the classroom, sitting at the intersection between utilizing technology as a medium for mathematics teaching and learning and the development of computational skills as an end in itself. The Game Play and Design Framework is a project-based instructional method to engage teachers and students in mathematics content by utilizing mobile technologies as a vehicle for highly active, highly social, collaborative game play and game creation. We utilize the Wearable Learning Cloud Platform (WLCP), a web-based technology tool and game editing platform we created, which enables teachers and students to play, create, and experience technology-augmented learning activities (Micciolo, 2018).
In this article, a 14-week professional development (PD) program is described, in which mathematics and STEM middle school teachers played, designed, tested, and implemented novel mathematics games with their own students. The article reports evidence suggesting that the PD framework is effective as students and teachers engaged, played, and created.
Teachers first played mathematics games (which use mobile devices for each player) and then designed and programmed their own games using the WLCP. Teachers then introduced this process and technology to their classes by having students play the games they created and later designing and programming games of their own.
This project introduces a new approach for teaching teachers how to improve both CT and math education. Through the Game Play and Design Framework, teachers and students both play mobile technology-based math games to deepen their knowledge of math concepts and create novel games through a visual programming language to engage with CT concepts.
We first describe background research on each of the intersecting areas, the PD framework, and the research study. As part of the results, we share examples of teacher- and student-created games and provide evidence of student learning gains from playing teacher-created games. We conclude with a discussion and interpretations suggesting that we are utilizing the benefits of mobile technologies, easily accessible programming tools, collaborative learning, and mobile technology-based games to develop students’ higher level thinking in STEM classrooms.
Literature Review
The Intersection of Technology, Games, CT, and Mathematics Education
Computer-Based Games
In recent years, using game play as an avenue for learning has gained in popularity, and a growing body of research has shown the effectiveness of playing games to learn and practice curricular content (Habgood & Ainsworth, 2011; Lester et al., 2013; Steinkuehler et al., 2012). For instance, educational games foster engagement and motivation among students while enhancing learning and promoting teamwork (Devlin, 2011). Such evidence suggests that games provide benefits to students beyond learning that could serve as effective, alternative activities for learning in STEM classrooms.
Engaging math games that are physically active extend learning beyond the seats of student desks as students can ground their content understanding in experiences all around the classroom. Educational games that combine movement with higher order cognition and that integrate learning content aim to engage students and, through object manipulation, make abstract concepts more concrete (Koedinger et al., 2008).
More recently, creating and deploying educational activities through mobile technologies has made using games for classroom instruction and practice more feasible as devices continue to become more compact and even wearable (Howison et al., 2011; Johnson et al., 2013). A growing body of literature has shown the benefits of using technologies for game play and game creation to support learning. For instance, our prior work has shown that playing physically active mathematics games with mobile technologies improved student learning compared to students who were taught the same content through traditional lectures (Arroyo et al., 2017). Such evidence shows the power of mobile technologies to extend learning beyond desks or computers to provide students with the opportunity to learn through active play.
Computational and Mathematical Thinking
In addition to playing games, creating games can benefit students’ learning. From a theoretical perspective, constructionist theory shares the notion that students learn by making (Papert, 1990). As such, in the process of creating a playable game, students engage in problem solving skills by planning, designing, and overcoming challenges.
In an early study, children created computer-based educational video games to teach fractions to younger elementary school children (Kafai & Resnick, 1996). The researchers reported that students learned not only through design but also about design and that they reached a level of reflection that went beyond traditional school thinking and learning, involving a variety of aspects of what is now considered CT.
Other studies report that students practice valuable skills through designing and creating games, such as creativity, critical thinking skills, and problem-solving skills (Dalal et al., 2009; Korte et al., 2007; Overmars, 2004). The game creation process requires students to understand the content of their game and allows them to teach and communicate the content in their own way. This approach encourages students to engage in deeper thinking about the mathematics content in their games, as well as overcoming and learning from the challenges involved with creating a game and working through an engineering design process.
The skills that students learn and refine through game creation make up the foundation of CT, which has been described as formulating problems and realizing solutions that can be implemented with technology (Wing, 2006, 2010). As CT skills, such as abstraction, pattern recognition, problem decomposition and error detection (Grover & Pea, 2013), have recently risen in importance in education (Weintrop et al., 2016), students should develop these skills from an early point in their education. To that effect, researchers and educators must create and deliver activities that challenge students to learn CT and explore problem solving methods.
When conceptualizing CT, we have found that several constructs overlap. The CT process lies at the intersection of several cyclical theoretical frameworks, including the engineering design process (from an engineering perspective; Ertas & Jones, 1996), problem solving (from a mathematics perspective; Polya, 1945), and the iterative design process (from an HCI perspective; Nielson, 1993). All of these constructs involve a kind of targeted thinking during a cyclical process: A problem is defined at a high level of detail with multiple possible solutions that need to be articulated and implemented to some degree, tested, and evaluated according to some criteria of success, and revised and redefined going back to the initial stage.
Professional Development in Computational Thinking and Problem Solving
While CT is a critical skill for students to learn in schools, many elementary and middle school teachers are not comfortable teaching these skills. Improving teacher knowledge and training teachers to implement CT into the classroom, requires providing high quality PD opportunities. To that end, extensive research has shown that the relationship between teachers, curriculum resources, and technology are all influential in if, and how, curriculum is implemented in classrooms.
The ways in which teachers adopt curriculum are dependent on their own knowledge and goals as well as the curriculum resources provided to them. Mishra and Koehler (2006) emphasized the three-way relationship between teacher knowledge of content, pedagogy, and technology to integrate technology into instruction effectively. Acknowledging that differences in teacher resources may influence their interpretation and use of curriculum resources and technology heightens the importance of supporting teachers and iteratively refining the materials and instruction given to teachers to support their understanding and implementation of new initiatives in their own classrooms.
Professional development programs offer a mechanism to provide this knowledge and training to teachers. According to Desimone (2009, 2011), high quality PD programs require a set of core features including (a) an emphasis on core content, (b) active learning, (c) coherence, (d) sustained duration, and (e) collective participation.
According to Desimone’s (2009) conceptual framework, teachers first should experience PD over time that both increases their knowledge and skills and also changes their beliefs. Teachers can then use their new knowledge, skills, and beliefs to alter and improve their approach to instruction in their own classrooms. In theory, these changes should relate to improved student outcomes. At the core, this framework asserts that for students to learn, teachers themselves need to learn and practice first.
Considering the overlap with computational and mathematical thinking, we created the Game Play and Design Framework to address STEM teachers’ lack of experience and training in how to teach CT to younger students by having teachers learn about and practice CT prior to applying this approach in their own classrooms. In the following section, we describe the goals and process of the Game Play and Design Framework.
Our Approach: The Game Play and Design Framework
The Professional Development Model
The Game Play and Design Framework is a series of game play and game creation experiences that allow teachers and students to integrate technology-based game play and game design in their own classrooms (Figure 1). The Framework consists of four stages that involve students and teachers as both game players and game creators. Students and teachers engage in tangible and social activities connected to mathematical content as game players and then become creators of educational games through a cyclical process. In turn, teachers and students reap the benefits of game play, such as collaborative learning and affective engagement with mathematics content, while at the same time obtaining the benefits of game creation, such as a deeper understanding of mathematics content and problem-solving skills. Each of the four stages of the framework are described in the following section.
Figure 1 The Game Play and Design Framework, in Four Stages: Teachers as Players (Stage 1), Teachers as Creators (Stage 2); Students as Players (Stage 3); Students as Creators (Stage 4)
Stage 1: Teachers as Players
Teachers are first introduced to the Wearable Learning Cloud Platform technology (described in the following section) by playing an existing active technology-based game. While the mathematical content of the game may be simple to teachers, the purpose of this activity is for them to have experience with the technology-based games as their students will do later in the process. As teachers engage with the technology and physically move through their environment, interacting with game props, they develop a context for understanding how the games are played and created, as well as a sense for how to incorporate mathematics content in a way that utilizes mobile technologies and physical movement.
Stage 2: Teachers as Creators
Following the experience of playing a game that incorporates mathematics, teachers then create and design their own math game in teams. During this process, teachers are expected to deepen their computational knowledge and develop more positive attitudes toward using games to develop computational and mathematical problem solving.
Stage 3: Students as Players
Once the teacher-created game is a functional product, teachers bring their games to their own classrooms. While teachers move into the role of game deployers and managers, students become game players within the context of the game that their teacher developed. As students play the technology-based game, they answer questions and solve problems related to class content by interacting with their peers, their environment, and the technology involved through active game play.
Stage 4: Students as Creators
After playing the games, students become creators as they design and program a math game of their own. Once the games are built, students run and debug the games before showcasing and playing their games with their classmates. During this process, students are expected deepen their mathematical knowledge, improve mathematical problem solving and creation, and develop positive attitudes toward CT.
Ultimately, the Game Play and Design Framework provides a novel approach for teachers and students to play and create instructional games augmented by mobile technologies to deepen student learning and promote computational and mathematical thinking skill development in STEM classrooms.
Our Testbed Technology: The WLCP
The WLCP (wearablelearning.org; Arroyo et al., 2017; Micciolo, 2018) is a web-based technology tool that allows users both to create and play original, active games for STEM learning with mobile devices. Users create accounts and access the WLCP in three different roles to explore both game play and game creation: Game Players, Game Editors, and Game Managers.
The WLCP was designed as a platform to play and create games for teachers and students. To that effect, rather than necessitating that schools download their own instance of the platform, users can log into the WLCP for free on any web browser on most devices, including desktop computers and smartphones. This accessibility is consistent with the mission of the WLCP to provide all students with opportunities to learn through game creation and game play.
Game Players
Students and teachers can use the WLCP to play existing games in their classrooms (Figure 2). The WLCP hosts a small library of existing games that users can play when they log in as Game Players. The platform provides a means of playing existing games and testing created games by serving them to smartphones. When users login as Game Players, they are able to access public games and games that they or their classmates have created. Students can also play games assigned by their teacher as class-wide activities.
Figure 2 The WLCP Serves Games, Smartphones and Wearable Devices, Allowing Students to Play Active Games in Their Own Classrooms

Game Editors
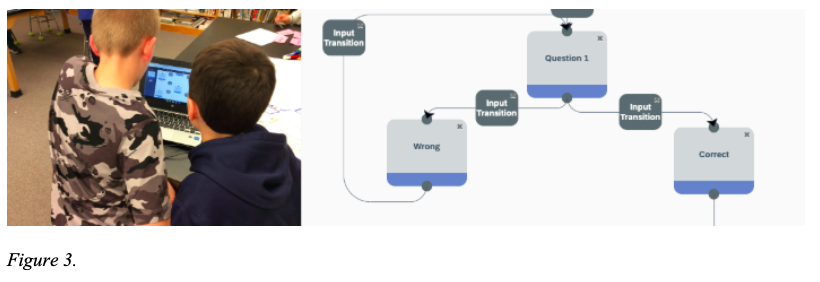
When users log into the WLCP as Game Editors, they have full access to the user-friendly, visual drag-and-drop game editor to create and refine games to be played on mobile devices (Figure 3). The WLCP is designed for programming novices so that middle and high school students can effectively use the game editing platform to create games with a wide variety of content, multiple levels, and players.
Teachers and students first plan out and design the behavior of their mobile devices as finite state machines on paper, then transfer them into our novel visual programming language, which assumes no prior programming knowledge. The first “state” in their design corresponds to the first message that their device displays when it is turned on. As students program their games, they specify states by choosing every behavior of the mobile device, including the text to be displayed on the screen (a question, hint, or welcome message) as well as lights, colors, buzzers, images, sounds and vibrations of each phone/smartwatch.
Middle school students (and their teachers) design and enter what their mobile devices will do when specific objects are scanned, what will happen when they click specific buttons, how the devices announce that the game is over, who has won, and so forth. As users move through the game creation process, they can also test-run and debug the game with immediate feedback from the WLCP through the run and debug feature of the editor, which simulates game play, to help ensure game functionality. Students use and implement finite state machines and advanced language, vocabulary, and understanding that is typically reserved for undergraduate students in computer science courses. Students observe the results of testing their mobile devices in the context of their games and make adjustments accordingly. Once the games have been created in the WLCP, multiple users can log in as Game Players to play.
Figure 3 The WLCP Platform Is Designed for Students to Program Games Through Finite State Machine Structures With Drag-and-Drop Game Elements in the Game Editor
Game Managers
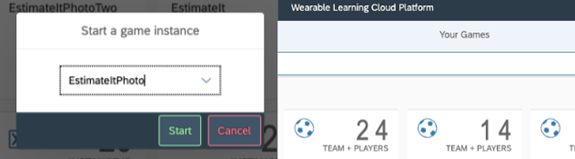
The WLCP allows teachers and students to act as Game Managers to facilitate game play in addition to acting in the roles of Game Editor and Game Player. As Game Managers, users activate games on the WLCP for a specific group of users to play (Figure 4). This function also allows multiple, simultaneous plays of the same game so that a teacher could allow 10 students or 30 students to play one game at the same time.
Figure 4 Left: Game Manager Select a WLCP Game for Their Students to Play. Right: Game Managers Can View Games That Are in Progress by Their Students
While the WLCP has been used in prior work with students and teachers and we have seen positive effects of playing and creating games through the WLCP in lab-based settings and in classrooms (Arroyo et al., 2017), a majority of this previous work involved our team of researchers directly delivering instruction for the WLCP to students. Less emphasis has been placed on how to train teachers to integrate this platform effectively and feasibly into their own curriculum. To remove researchers from this process and keep teachers in the role of facilitators, the goal of the current project was to examine the feasibility of training teachers to (a) create their own games, (b) effectively have their students play their developed games, and (c) have students create their own games through the WLCP in the classroom.
Research Questions
Through this project, we aimed to answer the following research questions:
- Can middle school STEM educators successfully play, design, and create games in the WLCP?
- Does classroom game play of the teacher-developed games improve students mathematics learning?
- Can middle school students successfully create games in the WLCP during classroom instruction?
Methodology
Participants
Twelve middle school STEM and math teachers completed the 14-week PD program. Of the 12 teachers, nine were middle school math teachers (one fifth grade, two sixth grade, three seventh grade, and one eighth grade), three were middle school STEM teachers (fifth-eighth grade), and one was an afterschool STEM activities coordinator. Together, roughly 400 students were exposed to the WLCP and Game Play and Design framework in their classes.
Procedure
To implement the Game Play and Design Framework in Figure 1, we developed a 14-week teacher PD program to introduce STEM educators to the WLCP and explore the benefits of active game play and creation with their own students and curriculum, following the four stages of the framework.The program encompassed all aspects of the Game Play and Design Framework involving both the playing and designing of multiplayer educational games for mathematics. The timeline of the implementation is described in detail in Table 1.
Table 1 Game Play and Design Professional Development Program Plan and Timeline
| Stage/Weeks | Description of Activity |
|---|---|
| Stage 1: Teachers as Players (Week 1) | Activity: Teachers play an existing game in the WLCP, called the Tangrams Race, followed by a discussion about the game content, and the role of the mobile technology to support players Materials: Geometric shapes with codes to play the Tangrams Race; a cell phone per teacher; observation sheet |
| Stage 2: Teachers as Creators (Weeks 2-7) | Activity: Teachers brainstorm game topics in groups of 2-3 people (Week 2) Teachers develop the game rules and design the game and finite state machine diagrams on paper (Week 3) Materials: Paper and markers |
| - | Activity: Teachers learn how to use the WLCP and then work in groups to program their games (Weeks 4-6) Materials: Presentation introducing the WLCP and the wearablelearning.org website |
| - | Activity: Teachers debug, revise, and play each others’ games! (Week 7) Materials: computer; http://wearablelearning.org; mobile device; any materials needed to play their designed game |
| Stage 3: Students as Players (Week 8) | Math Teachers: Math teachers design assessments and have their students play their WLCP-created game in the classroom Materials: internet; mobile devices; any materials needed to play their game |
| Stage 4: Students as Creators (Weeks 9-14) | STEM Teachers: STEM teachers lead their students in the Game Creation process, mirroring weeks 1-7 above Materials: Students create games and follow Weeks 1-7 |
During Weeks 1-7 of the program (corresponding to stages 1 and 2 of the framework), teachers worked in groups of two or three. Each group contained at least one STEM teacher and one math teacher to encourage collaboration between teachers who may have different areas of expertise and classroom experience.
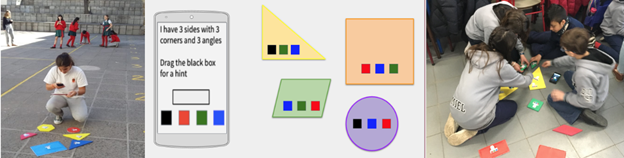
Stage 1 (Teachers as Players)was carried out during Week 1 when participating teachers played an existing geometry game in the WLCP, created by graduate students, called the “Tangrams Race” (Figure 5). This experience allowed them to see what a finished game product would look like in action.
Figure 5 Students Playing the Tangrams Race
Stage 2 (Teachers as Creators) was carried out during Weeks 2-7, when participating teachers first designed and then programmed original games in groups around their own curriculum and class-based needs. To start, teachers worked in teams to brainstorm potential math topics for the games. During Week 3, teachers began designing their games on paper, writing down rules of their games. During Week 4, they were given a lesson about finite state machine diagrams (FSMDs) and were encouraged to make a sketch (on paper) of the concrete behavior of the cell phones as a FSMD.
In Week 4, teachers were also introduced to the WLCP editor and received a short programminglesson, which basically consisted of how to transfer their FSMDs from paper onto the WLCP web site. After learning how to use the WLCP, they were ready to program their games. During Weeks 5-6, teachers programmed their games and were encouraged to use the run and debug function often to test their progress. The debugger would launch a simulator of a cell phone and show how the program would look when run on the mobile devices. During Week 7, teachers demonstrated, explained, and played one another’s games using cell phones and any other physical materials involved in the games.
During Stages 3 and 4 of the Framework, (Weeks 8-14), math and STEM teachers took different routes in their own classrooms. Math teachers finalized their games and had their students play the game they had created in their own classes (note that this corresponds to Stage 3, Students as Players). Teachers used cell phones and any other physical materials that they had created to run the games in the WLCP software.
STEM teachers also had their students play their finished games. However, after their students played the game, they continued the cycle and helped their students begin the game design process (corresponding to Stage 4, Students as Creators). Teachers also made their own set of instructions to teach their own classes how to program in the WLCP. By taking the time to learn how to use the WLCP, teachers each developed their own way to teach the game design process and programming to their students.
Measures and Approach to Analysis
The general approach to the measures and approach to analysis varied depending on the stage of the process.
Stages 1 and 2: Teachers as Players and Creators
The most important feasibility metric was teachers’ games, whether teachers produced full-fledged working games to continue through Stage 3. Additionally, we gathered two survey measures of Teachers’ General Experiences and Usability after using the WLCP on Week 7.
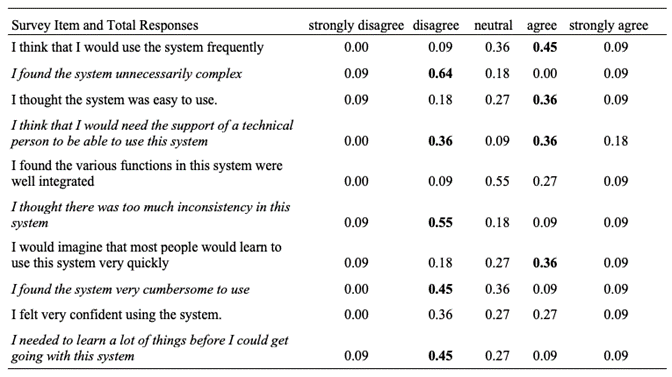
The first survey was the System Usability Survey (Brooke, 1986), which consists of ten 5-point Likert scale statements to be rated by users regarding their experience using the WLCP, such as “I needed to learn a lot of things before starting to use this system,” or “I felt very confident using this system.” The items assessed several constructs from affective to cognitive comfort on using the WLCP and carrying out the activity in general.
The second survey assessed the ease of use of the WLCP programming (game editor) tool on a 5-point Likert scale (5 = very easy to 1 = very hard). Teachers rated the usability of six programming aspects of game creation in the WLCP related to specific programming actions. Similar surveys have been used to assess students’ attitudes toward programming (Baser, 2013), perceptions of learning programming (Maltby & Whittle, 2000), and difficulties in learning programming (Tan et al., 2009).
Stage 3: Students as Players
We were interested in analyzing the effectiveness of the teacher-created games in the classroom for teaching and learning mathematics. Teachers designed and administered their own brief five- to six-question multiple-choice and short-answer pretests and mirrored posttests to students directly before and after playing the games in the classroom (Appendix A). Individually, the pre- and posttests for each teacher allowed us to analyze whether each game product was conducive to mathematics learning after student exposure to the mobile technology-based games.
Stage 4: Students as Creators
Three STEM teachers began the game creation process with their students. However, only one teacher was able to complete this process due to time constraints. Teachers kept online journals of the students’ game development process, including both positive aspects as well as difficulties faced in the classroom. We report the contents of the one completed online teacher journal, which includes eight pages of pictures and text updates. Additionally, in Week 14 students completed the ease of use survey similar to the teacher survey after their game creation process.
Results
Stage 2 Results: Teachers as Creators
Games Made by Teachers
The teachers produced a total of five games during the first seven weeks of the professional development program. Three of the five teacher groups successfully completed and pilot-tested their novel games in their own classrooms. While the remaining groups successfully created mathematics games using the WLCP, they were unable to implement the games in their own classrooms during the allotted 14-week period due to preparation for standardized testing and the ending school year. Below, we present three sample games that were developed by teachers in our professional development program. The three games cover material taught in 6th, 7th and 8th grade, each covering a different topic (integer addition and subtraction, percentages, and graphing equations).
Game 1: What’s My Line? What’s My Line?, a slope-equation and graph-matching game, was designed by an eighth-grade math teacher, Mrs. G and a fifth- through eighth-grade STEM teacher, Mrs. F. The learning objective of the game is to review the slope-intercept form of equations to ensure that students can read and interpret equations. Working in small teams, students are challenged to match equations presented on a mobile device with the corresponding line on a paper graph at one of seven different stations around the classroom (Figure 6). The goal of the game is to move through all nine stations to correctly match each equation to one line on each graph before the other teams can finish the game.
Figure 6 One of the Seven Graph Stations Featured in What’s My Line?
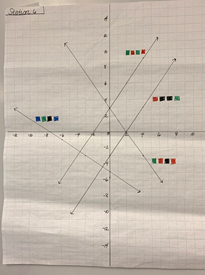
Small teams choose the slope that matches an equation shown on their mobile device. Teams then drag and drop the correct color sequence (e.g., blue, green, black, pr blue) and receive immediate feedback on their phone.
Let’s Shop. Another game, Let’s Shop, was designed by two seventh-grade math teachers, Mrs. S and Mrs. B, and one fifth- through eighth-grade STEM teacher, Mrs. M. The game features real-life scenarios where students are challenged with finding the correct price or discount of an item associated with a word problem. Example problems include calculating the tip at a restaurant, finding the sale price of a clothing item, or calculating the tax on a purchase (Figure 7). In groups, students work to figure out the answer and then locate the correct answer on a card somewhere in the classroom as if they are on a scavenger hunt. Players enter each answer into the WLCP on a cell phone. Correctness feedback on the submitted answer and hints to support problem-solving are provided to students. The goal of the game is to be the first team to complete all nine problems.
Figure 7 An Example Screen Display From the Game, Let’s Shop

Integer Hopscotch. A third game, Integer Hopscotch, was designed by a sixth-grade math teacher, Mrs. T, a seventh-grade math teacher, Mrs. L, and one sixth- through eighth-grade STEM teacher, Mrs. D. The game gives students word problems that relate to addition and subtraction with positive and negative integers and has players walk along a 20-foot number line to find the answer to each problem. Students input each answer into the WLCP to receive immediate feedback, and they always have the option to request a hint throughout the game. The goal of the game is to work in pairs to complete all of the integer addition and subtraction problems by moving along the number line.
Examining the Usability of the WLCP for Teachers
To examine the usability of the WLCP for teachers we administered the System Usability Survey (SUS) which was released by John Brooke in 1986. This survey is widely used to assess the usability of different programs and has been referenced in over 600 publications (Sauro, 2011). Eleven teachers filled out the system usability survey about their experience using the WLCP during the Teachers as Creators part of the PD program. The most common responses to each statement are reported in Table 2.
Table 2 Teachers Reported Their Overall Impressions of the WLCP After Designing Their Own Games
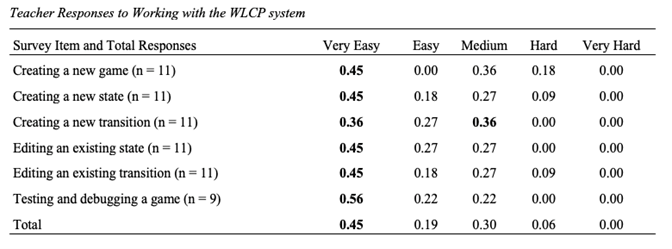
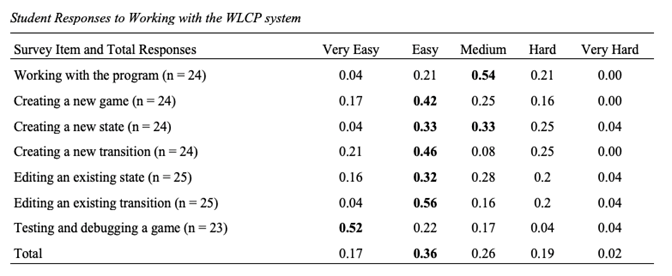
Teachers also completed a survey to assess the ease of use of the WLCP on a 5-point Likert scale, with item responses ranging from very easy to very hard. Teachers rated the usability of six programming aspects of game creation specific to the WLCP. We created the six items to correlate with specific programming actions within the game editing platform, as shown in Table 3. In general, teachers reported having positive experiences with the WLCP and reported positive outlooks on the usability of the WLCP in the future. Teachers also seemed generally confident in their ability to program using the WLCP.
Table 3 Teachers Ranked the Ease or Difficulty of Using Specific Programming Features in the WLCP
Stage 3 Results: Did Students Learn Math When Playing Teacher-Created Games?
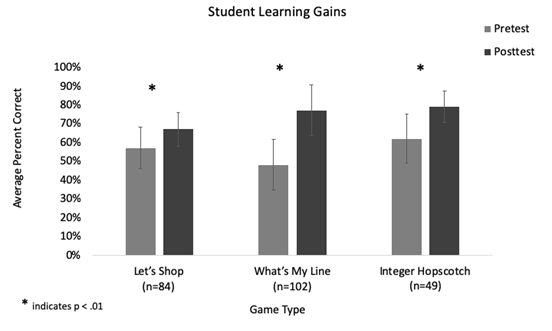
To analyze the effectiveness of these games in the classroom, teachers designed and administered brief five- to six-question, mirrored, multiple-choice pretest and posttests to students directly before and after playing the games in the classroom. We conducted repeated measures t-tests on the pretest and posttest scores of the students who played their teacher’s game. Following are results from three classrooms (Figure 8). Scores are reported in percentages.
Figure 8 Playing the Games Designed by Their Teachers Led to Significant Learning Gains by Students in Brief Pre- and Posttest Assessments
What’s My Line?
Mrs. G tested the game What’s My Line? with four of her eighth-grade math classes (102 students total). Students began the class by taking a pretest to assess their knowledge of slope-equation and graph matching. This topic was focused on earlier in the year, and Mrs. G noticed that her students continued to struggle with this content. To play the game, students were split into groups of three to four players with one cell phone per team. After completing the game, students took the posttest designed by Mrs. G and gave general feedback on their experience in a classroom discussion. A repeated measures t-test revealed that the 102 eighth-grade students who played What’s My Line? improved significantly from the brief pretest (M = .48, SD= .27) to posttest (M = .77, SD = .27), t(101) = 7.15, p < .001.
Let’s Shop
Mrs. S and Mrs. B tested the game Let’s Shop! with eight of their seventh-grade math classes (84 students total). However, only Mrs. S collected pretest and posttest data due to scheduling and time constraints. Mrs. S gave her students a pretest on percentages and identified weak point for her students at the beginning of class.
Both teachers split their classes up into groups of three to four players, with one cell phone per group. After playing the game, Mrs. S administered her posttest to students. A repeated measures t-test showed that the 84 seventh-grade students who played Let’s Shop improved significantly from the brief pretest (M = .57, SD = .22) to posttest (M = .67 , SD = .18 ), t(83) = 3.12 , p = .002.
Integer Hopscotch
Mrs. T tested the game with two sixth-grade classes (49 students total). She administered a brief pretest on students’ knowledge of integer equations at the beginning of class before partnering students to play the number line game in pairs. Each pair of students was given a cell phone to play the game and took turns walking along the number line to find the answer from one problem to the next. After playing the game, the students took the posttest. A repeated measures t-test revealed that the 49 students who played Integer Hopscotch improved significantly from the brief pretest (M = .62, SD = .26) to posttest (M = .79 SD = .17), t(48) = 6.39, p < .001.
Stage 4 Results: Students as Creators
An Example Student-Created Game and Journaling about Students
Only one of the three STEM teachers were able to complete the game creation process with her class due to time constraints and state testing. Mrs. F, a STEM teacher, led her fiftg-grade class of 27 students through the Game Creation process, following the same curriculum that the teachers completed as participants in the PD program. Mrs. F kept an informal online journal reporting the process with updates and pictures showing how the students progressed over a 4-week period during 50-minute class sessions.
In this journal, we observed both text and picture evidence of the students completing the game creation process from start to finish. After playing an existing game, brainstorming in groups, and completing the paper diagrams depicting how they would program their games in the WLCP (Figure 9), students began programming on the WLCP platform in their groups. They then completed programming their game, gathered and created any materials necessary for gameplay (such as cards, balls, and other props), then tested and debugged their games in their groups.
As a final step, all of the groups were able to play their completed games with the rest of their class, as reported in the journal. Ms. F reported, “A few kids were naturals at programming,” and “It’s a nice process to see the kids working together. They are anxious to see their games played!” As a final step, the students were able to play each other’s’ games in the class. Ms. F reported, “They are so excited! Played one of the games today. Kids loved it!”
Figure 9 To Fully Engage in the Game Design Process, Students Begin by Brainstorming Game Ideas Together in Groups (Left), Then Learn About Finite State Machines and Practice Designing Their Own (Middle) Before Programming Their Game Into the WLCP (Right)

Usability of the WLCP for Students
Students who completed the Students as Creators portion of the Game Play Design Framework also completed the ease-of-use survey that the teachers took to assess general usability of the WLCP. Out of the 27 students that completed the game creation process, 25 completed the survey. The most common responses are displayed in Table 4.
Table 4 Students Ranked the Ease or Difficulty of Using Specific Programming Features in the WLCP
Discussion
This paper introduces the Game Play and Design Framework and the WLCP tool, which introduces teachers and students to computational thinking through math game play and creation. To test the framework, the Game Play and Design PD program was designed and deployed across 14 weeks with middle school STEM teachers. Small groups of teachers designed games during the PD program, programmed the behavior of mobile devices by specifying finite state machine diagrams in WearableLearning.org, debugged their games within the environment, and then pilot tested those technology-based games in their own classrooms.
Outcomes of the Game Play and Design Professional Development Program
The first 7 weeks of the program were largely successful. Through the PD program, teachers were able effectively to complete the design process and produce playable math games for classroom use in the 7-week period. Teachers seemed generally confident in their abilities to use the tool as creators and in their ability to program using it. Importantly, most teachers reported having positive experiences with the WLCP and reported positive outlooks on the usability of this web-based system in the future.
Once teachers were ready to test their games in the classroom, they were also successful game managers, using the WLCP for their own students to play their games on cell phones in the classroom. Playing these games seemed to impact students’ mathematics knowledge positively, as evidenced by changes in pre-post assessments. These results have implications for using teacher-created games in the WLCP in the classroom as an additional learning activity for mathematics students.
The second half of the program (Weeks 8-14) was also feasible for one of our STEM teachers. She successfully implemented the game creation part of the program in her own classroom. She was able to effectively share and implement what she had learned through the professional development program with her students. As a result, students were able to produce games which they were able to test with their classmates. Her students also reported confidence in their programming abilities within the WLCP.
This program has prepared participating STEM and math teachers to implement the play-create process with their own students using the WLCP website to cultivate a deeper understanding of mathematics content through engaging activities. This ability for teachers to learn throughout the Game Play and Creation PD Program and then teach the content suggests that the framework and the WLCP tool is feasible for classroom use in middle school math classrooms. While we have evidence only from one teacher, she was successfully able to lead her 27 students through this process.
More broadly, we interpret these outcomes as evidence that the proposed framework and technology tool, the WLCP, are promising as STEM learning tools for use by middle school teachers and students. As players, students and teachers engage in collaborative learning to solve problems. As creators, students and teachers go beyond problem solving and display computational thinking by considering which games would be interesting to other students, thinking about how to blend mathematical material into challenges in the game, and then thoroughly planning the mechanics of the game and specifying the behavior of the devices as a finite state machine. Ultimately, this work aims to introduce a STEM learning curriculum in which students and teachers play, design, and create mathematics games to encourage learning and engagement and develop both teachers’ and students’ computational thinking and mathematics skills.
Limitations and Future Work
This work represents our first attempt at scaling up the Game Play and Design Framework using the WLCP. While it appeared to be successful overall, we realized through the process that there were limitations, challenges, and areas that we would like to improve upon and explore in the future.
First, we did not collect any data on teachers’ and students’ experiences during game play. Videotaped observations and surveys could be used to understand better and code teachers and students experiences and allow us insights into how the game playing experience could be improved.
While each teacher led a classroom discussion on students’ experiences after playing the games, a formal survey on students’ experience would be more beneficial to assess and refine the game play portion of the Game Play and Design Framework. In the next iteration of this program, we intend to use measures of the game playing experience to explore student engagement and content learning gains to better understand the benefits of game play as opposed to game creation. A future goal is to compare the impact of game playing versus game creation, or both, on mathematics learning, as the latter most likely encourages deep thinking about mathematics concepts through problem posing, and also makes students think about how to help or support future problem solvers (Arroyo & Woolf, 2003; Silver & Cai, 1996).
Next, we want to design better ways to assess student learning of mathematical content. Although three games were tested with classwide use, not all of the created games were played to assess student learning gains. The PD program was conducted in the spring, prior to, and during, state-mandated standardized testing. This timing introduced unforeseen conflicts with teacher availability and reduced teachers’ abilities to introduce game play and game creation in the classroom fully at the expense of test preparation. For instance, one teacher did not administer pretests and posttests to her students during the game playing portion of the program to minimize time away from content instruction.
Even with the pressure of state testing, however, teachers were excited and interested enough in the project to introduce this platform and their self-created games to their classes. Future versions of the program for educators will take place in the fall semester of the school year to mitigate scheduling and participation issues that arose from the upcoming standardized testing.
Additionally, this study did not include any pre or post measures of teachers or students computational thinking (CT), which limits our ability to draw any concrete conclusions about students’ and teachers’ development of CT skills. More broadly, the game creation process could benefit students beyond developing content knowledge by also exercising facets of CT (Wing, 2006).
While CT was not directly measured during this program, the design process, including highly precise specification of games and the mobile technology behaviors in the game, exercises students’ CT through decomposition, abstraction, and debugging. Prior work has shown that students who create games demonstrate facets of CT that are central to success in STEM fields, such as higher performance in problem solving, strategy use, system analysis and decision-making skills (Akcaoglu & Koehler, 2014; Vos et al., 2011). Future implementations of the Game Play and Design Framework through educator PD programs and classroom studies intend to encompass measures of CT to assess whether students develop such areas of higher level thinking skills through the game creation component of the Game Play and Design Framework.
Similarly, no assessments were given to the students or teachers regarding their abilities to use the WLCP outside of the PD program. We acknowledge that this limits our ability to assess the usability of the WLCP beyond the program and to assess teachers’ ability to use the framework independently after completing the program. Participants seemed generally confident in their abilities to program and use different aspects of the WLCP. However, further assessments to measure students’ experiences with game play and game creation are needed to assess their full understanding of the program. Future versions of the program will include measures to further assess student experience as creators and follow up measures with teachers to explore whether they continue to use the WLCP after the program concludes.
Implications for Teacher Education
The WLCP, the Game Play and Design Framework, and the PD program can directly be used both by teachers and students to improve engagement and learning of STEM in the classroom, by providing the freedom to create and play educational games with a low-barrier entry for novice programmers. While this PD program focused on mathematics games, the WLCP can be used by educators and learners in other subjects to play and create curriculum-specific games to support teacher and student autonomy as well as student engagement and learning.
Overall, the results presented here support the feasibility and usability of the Game Play and Design Framework and provide examples of how the WLCP can be used by teachers and students in classrooms to promote learning, engagement, and problem-solving through game play and creation. The teachers’ interest and fidelity to the program suggest that this PD program and technology tool are promising may be feasible and worthwhile for STEM teachers to adopt in their classrooms as a way to integrate technology and concepts of CT into their existing STEM curricula.
References
Akcaoglu, M., & Koehler, M. J. (2014). Cognitive outcomes from the Game-Design and Learning (GDL) after-school program. Computers & Education, 75, 72-81.
Arroyo, I., Micciollo, M., Casano, J., Ottmar, E., Hulse, T., & Rodrigo, M. M. (2017). Wearable Learning: Multiplayer embodied games for math. In Proceedings of the Annual Symposium on Computer-Human Interaction in Play (pp. 205-216). Association for Computing Machinery.
Arroyo, I., & Woolf, B. P. (2003). Students in AWE: Changing their role from consumers to producers of ITS content. Proceedings of the Workshop “Advanced Technologies for Mathematics Education,” 11th International Conference on Artificial Intelligence in Education. Sydney, Australia.
Baser, M. (2013). Attitude, gender and achievement in computer programming. Online Submission, 14(2), 248-255.
Brooke, J. (1986). System usability scale (SUS): A quick-and-dirty method of system evaluation user information. Digital Equipment Co Ltd.
Dalal, N., Dalal, P., Kak, S., Antonenko, P., & Stansberry, S. (2009). Rapid digital game creation for broadening participation in computing and fostering crucial thinking skills. International Journal of Social and Humanistic Computing, 1(2), 123-137. https://doi.org/10.1504/ijshc.2009.031002
Desimone, L. M. (2009). Improving impact studies of teachers’ professional development: Toward better conceptualizations and measures. Educational Researcher, 38, 181–199. https://doi.org/10.3102/0013189X08331140
Desimone, L. M. (2011). A primer on effective professional development. Phi Delta Kappan, 92(6), 68–71. https://doi.org/10.1177/003172171109200616
Devlin, K. (2011). Mathematics education for a new era: Video games as a medium for learning. A K Peters, Ltd.
Ertas, A., & Jones, J. C. (1996). The engineering design process. John Wiley & Sons Inc.
Grover, S., & Pea, R. (2013). Computational thinking in K–12: A review of the state of the field. Educational Reer, 42(1), 38-43. https://doi.org/10.3102/0013189X12463051
Guzdial, M. (2008). Education: Paving the way for computational thinking. Communications of the ACM, 51(8), 25–27. https://doi.org/10.1145/1378704.1378713
Habgood, M. P. J., & Ainsworth, S. E. (2011). Motivating children to learn effectively: Exploring the value of intrinsic integration in educational games. Journal of the Learning Sciences, 20(2), 169–206. https://doi.org/10.1080/10508406.2010.508029
Howison, M., Trninic, D., Reinholz, D., & Abrahamson, D. (2011). The Mathematical Imagery Trainer: From embodied interaction to conceptual learning. In G. Fitzpatrick, C. Gutwin, B. Begole, W. A. Kellogg, & D. Tan (Eds.), Proceedings of the annual meeting of The Association for Computer Machinery Special Interest Group on Computer Human Interaction: “Human Factors in Computing Systems” (CHI 2011; pp. 1989-1998). ACM Press.
Johnson, K., Pavleas, J., & Chang, J. (2013). Kinecting to mathematics through embodied interactions. Computer, 46(10), 101–104. https://doi.org/10.1109/MC.2013.363
Kafai, Y. B., & Burke, Q. (2014). Connected code: Why children need to learn programming. MIT Press.
Kafai, Y. B., & Resnick, M. (1996). Constructionism in practice: Designing, thinking, and learning in a digital world. Lawrence Erlbaum Associates.
Koedinger, K. R., Alibali, M. W., & Nathan, M. J. (2008). Trade-offs between grounded and abstract representations: Evidence from algebra problem solving. Cognitive Science, 32(2), 366–397. https://doi.org/10.1080/03640210701863933
Korte, L., Anderson, S., Pain, H., & Good, J. (2007, June). Learning by game-building: a novel approach to theoretical computer science education. ACM SIGCSE Bulletin, 39(3), 53-57.
Lester, J. C., Ha, E. Y., Lee, S. Y., Mott, B. W., Rowe, J. P., & Sabourin, J. L. (2013). Serious games get smart: Intelligent game-based learning environments. AI Magazine, 34(4), 31–45. https://doi.org/10.1609/aimag.v34i4.2488
Likert, R. (1932). A technique for the measurement of attitudes. Archives of Psychology, 140, 1–55.
Lockwood, J., & Mooney, A. (2017). Computational thinking in education: Where does it fit? A systematic literary review. National University of Ireland Maynooth. https://arxiv.org/pdf/1703.07659.pdf
Maltby, J. R., & Whittle, J. (2000). Learning programming online: Student perceptions and performance. In Proceedings of the ASCILITE 2000 Conference. https://www.ascilite.org/conferences/coffs00/papers/john_maltby.pdf
Micciolo, M. (2018). Designing a visual programming language for creating multiplayer embodied games. (Master’s thesis). Worcester Polytechnic Institute, Massachusetts. https://digitalcommons.wpi.edu/cgi/viewcontent.cgi?article=2271&context=etd-theses
Mishra, P., & Koehler, M. J. (2006). Technological pedagogical content knowledge: A framework for teacher knowledge. Teachers College Record, 108(6), 1017–1054.
National Research Council. (2012). A framework for K-12 science education: Practices, crosscutting concepts, and core ideas. National Academies Press. https://doi.org/10.17226/13165
Nielsen, J. (1993). Usability engineering. Academic Press.
Overmars, M. (2004). Teaching computer science through game design. Computer, 37(4), 81–83. https://doi.org/10.1109/MC.2004.1297314
Papert, S. (1990). Introduction: Constructionist learning. In I. H. (Ed.), Constructionism. MIT Press.
Pólya, G. (1945). How to solve it: A new aspect of mathematical method. Princeton, NJ: Princeton University Press.
Sauro, J. (2011). A practical guide to the system usability scale: Background, benchmarks and best practices. Measuring Usability LLC.
Silver, E., & Cai, J. (1996) An analysis of arithmetic problem posing by middle school students. Journal for Research in Mathematics Education, 27(5), 521-539.
Steinkuehler, C., Squire, K., & Barab, S. (Eds.). (2012). Games, learning, and society: Learning and meaning in the digital age. Cambridge University Press. https://doi.org/10.1017/CBO9781139031127
Tan, P. H., Ting, C. Y., & Ling, S. W. (2009). Learning difficulties in programming courses: Undergraduates’ perspective and perception. In Proceedings of the 2009 International Conference on Computer Technology and Development (Vol. 1, pp. 42-46). IEEE.
Vos, N., Van Der Meijden, H., & Denessen, E. (2011). Effects of constructing versus playing an educational game on student motivation and deep learning strategy use. Computers & Education, 56(1), 127-137.
Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., & Wilensky, U. (2016). Defining computational thinking for mathematics and science classrooms. Journal of Science Education and Technology, 25(1), 127-147.
Wing, J. M. (2006). Computational thinking. Communications of the ACM, 49(3), 33–35. https://doi.org/10.1145/1118178.1118215
Wing, J. M. (2010). Computational thinking: What and why? The Link. https://www.cs.cmu.edu/link/research-notebook-computational-thinking-what-and-why
Appendix A
Example of the Pre/Posttest Used Before and After Playing Let’s Shop
1. 100 7th graders were outside for gym. 35 students played basketball, 25 students played football and the rest ran on the track. What percent of 7th graders ran on the track?
- 50%
- 40%
- 90%
- 45%
2. Michelle and Karen went to dinner. The bill was $44 including tax. They wanted to leave a 15% tip. How much did they leave for the tip?
- $4.40
- $8.80
- $6.60
- $13.20
3. Ashton bought a pair of sneakers that was originally $60. They were on sale for 30% off. How much did Ashton pay for the sneakers?
4. Silko Honda bought a used car for $900. They cleaned it up and want to sell it for a mark up of 20%. How much will they sell the car for?
- $180
- $1080
- $820
- $1820
5. Today all snacks are 50% off at BJs. Mrs. Areson had $60 worth of snacks for the snack cart in her carriage. When she got to the register everything was an additional 20% off. How much did Mrs. Areson pay for the snacks?
![]()